シリコンナノ結晶の発光寿命分布の再評価
要約
ナノ結晶の集合体の発光ダイナミクスは、不均一に広がったサンプルの放射率と非放射率のサイズ依存性や粒子間相互作用など、さまざまなプロセスによって複雑になります。これにより、非指数関数的減衰が発生します。これは、シリコンナノクリスタル(SiNC)の特定のケースでは、コールラウシュまたは「拡張指数」(SE)関数で広くモデル化されています。まず、exp [−( t に続く発光減衰の母集団減衰関数を導出します。 / τ) β ]。次に、発光減衰または母集団減衰のいずれかがこの関数に従うと仮定して計算された分布と平均時間を比較し、結果がβで大幅に異なることを示します。 次に、これら2つのタイプのSE関数と他のモデルを、平均サイズが異なる2つの熱成長SiNCサンプルからの発光減衰データに適用します。平均寿命は、実験のセットアップと選択したフィッティングモデルに強く依存しますが、いずれもアンサンブル崩壊のダイナミクスを適切に説明しているようには見えません。次に、周波数分解分光法(FRS)技術をSiNCに適用して、寿命分布を直接抽出します。レート分布の半値幅は約0.5十年で、主にやや高周波で歪んだ対数正規関数に似ています。 TRS法とFRS法の組み合わせは、広い発光スペクトルを持つNC材料の発光ダイナミクスを明らかにするのに最も適しているようです。
はじめに
コロイド状ナノ粒子は、触媒作用、医療、オプトエレクトロニクスアプリケーションなどのさまざまなアプリケーションで使用できます[1,2,3,4]。半導体ナノ粒子は、発光、光起電、および光触媒の用途に特に関心があります[5、6]。シリコンナノ結晶(SiNC)は、調整可能な発光特性[7]と、シリコンの存在量と生体適合性[8]により、現在注目されています。ナノ粒子ベースの技術を開発するには、関連する光電子特性に関する深い知識が必要であり、時間分解分光法はこの目的のための貴重なツールであることがよくあります。
SiNCの発光寿命は通常、基本形exp [−(λt)を持つ拡張指数(SE)関数でモデル化されます。 ) β ]、ここで分散パラメータβ 0から1までの値を取りますλ はレートパラメータであり、 t 時間です。この関数は、「指数関数よりも遅い」と表現されることが多く、寿命が長くなる方向に減衰率が非対称に分布していることを意味します。一度β およびλ パラメータは、発光減衰曲線をフィッティングすることによって発見されており、対応する減衰率分布はほぼ再構築できます[9]。
シリコンやその他の半導体量子ドットにおけるSE発光の減衰の起源は、過去20年間で激しく議論されており、最近も議論が続いています[10]。ナノ結晶の近接した集団におけるキャリアトンネリングとトラッピング[11]、不均一に広がったサイズ分布[12]、サイズに依存する電子-フォノン結合[10]など、崩壊ダイナミクスにおけるSEの出現についてさまざまな説明が提案されています。 、および非放射再結合のバリア高さの分布[13]、後者は多孔質シリコンの以前の提案[14]と同様です。明らかに、SiNCおよびより一般的な半導体ナノ結晶の発光メカニズムを理解するには、速度分布の知識が必要です。
SiNCに関する以前の文献の多くでは、拡張指数関数的減衰は、通常、他の可能な分布の分析なしに、先験的に想定されていました。 SEは視覚的によくフィットする傾向があります(つまり、最適な線は「目で見て」データとよく一致しているように見えます)。さらに、以前の作品の大部分、たとえば[15]では、人口の崩壊または発光の崩壊が実際にモデル化されているかどうかについての明確さの欠如があります。これらは導関数によって関連付けられており、サンプルの減衰タイムスケールを理解するために正しい式を使用する必要があります[16]。また、検出器の応答関数は、アンサンブル発光スペクトルが広いため、SiNCで測定された発光減衰曲線に大きな影響を与える可能性があります。それにもかかわらず、責任が考慮されることはめったになく、さまざまな調査の結果を比較することは困難です。最後に、これまでの研究では、シリコンナノ結晶の分析に周波数分解分光法(FRS)を使用しようとしたことはありません。原則として、FRSでは、モデルを事前に想定せずに寿命分布を抽出できます。
この論文の目的は、シリコンナノ結晶の発光ダイナミクスを測定、モデル化、および解釈するためのアプローチを確立することです。これが、文献でしばしば矛盾する結果の広大な多様性をよりよく理解し、異なる測定値間のより良い一致、または少なくともより一貫性をもたらし、発光メカニズムをよりよく理解するのに役立つことが期待されます。
基本理論
3つのモデルを比較します。Siナノ結晶に広く使用されている拡張指数関数、最近SiNCに最初に適用された対数正規減衰分布[17]、および二分子減衰です。どのモデルでも、強度関数 g の積分で表される放出確率密度関数 ( t )、時間 t ' t 'に残っている励起の割合に関連しています [16]によると。
$$ {\ int} _0 ^ tg \ left({t} ^ {\ hbox {'}} \ right)dt =1- \ frac {c_t} {c_0}、$$(1)ここで c t および c 0 は、時間 t で励起されたNCの数です。 そして最初に。確率密度関数は、時間0から t の間に放出された光子の割合を表します。 放出されたフォトンの総数に対する相対値。人口の減衰が一次反応速度式(つまり、「単分子」再結合)に従う場合、 dc が得られます。 t / dt = − λc t 、ここでλ =1 / τ 0 、通常の c につながります t / c 0 =exp [− λt ]および g ( t )=λ⋅ exp [− λt ]式の両側の時間微分を取った後。 1.ウィンドウ dt 'で測定される発光強度のため、導関数が必要です。 その間隔での励起された割合の変化に比例します。
放射率と非放射率の両方を考慮する場合、総減衰率λを置き換えます。 λ R + λ NR g ( t )=(λ R + λ NR )exp [−(λ R + λ NR t ] =λ R exp [−(λ Ri + λ NR ) t ] + λ NR exp [−(λ R + λ NR ) t ]最初の項のみが測定可能であり、
によって与えられる時間分解分光法(TRS)の測定強度が得られます。 $$ g(t)={\ lambda} _R \ exp \ left [-\ left({\ lambda} _R + {\ lambda} _ {NR} \ right)t \ right]。 $$(2)データの近似に使用される減衰関数 I t = A・ exp(− λt )+ dc、追加の任意のプリファクター A でスケーリング 、これは検出効率と励起されたナノ粒子の数に依存し、適切なスケールにつながります。 DCオフセットは通常、別のフィッティングパラメータとして減衰関数に追加されます。
拡張指数緩和の場合、励起されたエミッターの割合は、
に従って減衰します。 $$ \ frac {c_t} {c_0} =\ exp \ left [-{\ left({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right]。 $$(3)ここで、λ SE は、拡張指数関数的減衰率(1 /τに等しい)です。 SE )。 これを式に挿入します。 1で、前と同じように両側の導関数をとると、次の式で与えられる放出確率関数が得られます。
$$ g(t)={\ beta \ lambda} _ {SE} ^ {\ beta} {t} ^ {\ beta -1} \ exp \ left [-{\ left({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right]。 $$(4)頻度の分布を推定する方法 H (λ )それは式につながります。 3は、逆ラプラス変換[9]を使用して示され、βの減少とともに広がる分布を生成します。 高周波に偏っています。
残念ながら、式では。 4、プレファクターを放射部分と非放射部分に分離することはできません。これは、式4はλに対してのみ正しく正規化されます NR = 0 [16]であり、PL減衰曲線から得られる寿命分布はこの方法でのみ理解されます。さらに、プリファクターには時間依存の項があります。したがって、集団崩壊は、発光崩壊と比較して異なる時間依存性を持っています[16、18]。 τの値を取得するため SE およびβ 適切な平均寿命を抽出できる人口減少については、式(1)を使用する必要があります。 4観測された減衰をモデル化するために、 g を置き換えます。 ( t )測定された減衰関数 I t :
$$ {I} _t =A {\ beta \ lambda} _ {SE} ^ {\ beta} {t} ^ {\ beta -1} \ exp \ left [-{\ left({\ lambda} _ {SE } t \ right)} ^ {\ beta} \ right] + \ mathrm {dc}。 $$(5)式で。 5、スケーリングパラメータ(βも吸収できます およびλ プリファクターの項)とDCオフセットがフィッティングパラメーターとして挿入されました。平均寿命は
によって与えられます $$ \ left \ langle {\ tau} _ {SE} \ right \ rangle =\ frac {\ tau_ {SE}} {\ beta} \ Gamma \ left [\ frac {1} {\ beta} \ right]、 $$(6)ここで、Γ はガンマ関数を表し、平均減衰時間は
$$ \ left \ langle t \ right \ rangle ={\ tau} _ {SE} \ frac {\ Gamma \ left(2 / \ beta \ right)} {\ Gamma \ left(1 / \ beta \ right)} 。 $$(7)以前の多くの研究では、「標準」の拡張指数exp [−(λ)を使用するのが一般的でした。 SE t ) β ]人口減衰の代わりに発光減衰をモデル化する。したがって、
によって与えられる正規化された強度関数があります。 $$ g(t)=\ frac {\ lambda_ {SE} \ beta} {\ Gamma \ left(1 / \ beta \ right)} \ exp \ left [-{\ left({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right]。 $$(8)式8は、 t 間の積分が行われるように正規化されています。 =0および∞は1に等しい。対応するフィッティングモデルは単純に
$$ {I} _t =A \ exp \ left [-{\ left({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right] + \ mathrm {dc}。 $$(9)式9は広く適用されており、(式4のように)式9が8は、100%の絶対量子効率(AQY)に対して厳密に正規化されています。見落とされがちな点は、τを抽出できないことです。 SE (=1 / λ SE )およびβ 式によってモデル化された発光減衰から。 9そしてそれらを使用して式で平均時間を計算します。 6と7。本質的に、式。 4と8は異なる強度減衰モデルであり、異なる母集団減衰関数、平均時間、および減衰率分布を期待する必要があります。
式(1)で与えられる強度関数につながる人口減少を見つけるために。 9、式から取得するために行ったのと同じプロセスを適用します。 4から式。 5、ただし逆に、つまり:
$$ \ frac {c_t} {c_0} =1- \ frac {\ lambda_ {SE} \ beta} {\ Gamma \ left(1 / \ beta \ right)} {\ int} _0 ^ t \ exp \ left [ -{\ left({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right] \ cdot \ mathrm {dt}。 $$(10)いくつかのステップの後、式の解は次のようになります。 10は
$$ \ frac {c_t} {c_0} =\ frac {1} {\ Gamma \ left(1 / \ beta \ right)} \ Gamma \ left [1 / \ beta、{\ left({\ lambda} _ { SE} t \ right)} ^ {\ beta} \ right]。 $$(11)式11は、式11で与えられる強度減衰から得られる母集団減衰です。 8.通常の方法で平均寿命を見つけることは
につながります $$ \ left \ langle {\ tau} _ {SE} \ right \ rangle ={\ tau} _ {SE} \ frac {\ Gamma \ left(2 / \ beta \ right)} {\ Gamma \ left(1 / \ beta \ right)} $$(12)の平均減衰時間 $$ \ left \ langle t \ right \ rangle ={\ tau} _ {SE} \ frac {\ Gamma \ left(3 / B \ right)} {2 \ Gamma \ left(2 / \ beta \ right)} 。 $$(13)
最後に、度数分布は( 1 / λ )・H (λ )、ここで、前と同じように、 H (λ )は、参考文献で計算された分布です。 [9]式で与えられる人口崩壊の場合。 3.これらの結果は表1にまとめられています。
<図>2つのSE式の違いは重要です(図1)。文献では、強度の減衰が A・によってモデル化されていることがよくあります。 exp [−( t / τ SE ) β ] + dc(つまり、式9)次に、平均時間は式を使用して計算されます。 6と7。これは数学的に正しくないようです。 6と7は、式(1)で与えられる強度減衰から導き出されます。 4、式ではありません。 8.たとえば、τを取る SE =100μsおよびβ =0.7、図1に示すように、exp [−( t / τ SE ) β ]、式(1)を使用した場合の127μsと比較して、199μs(式12)の平均時定数が見つかります。 6.平均減衰時間についても同様の違いが見られます(式7および13)。さらに、特性寿命を推定するための東カストナー法[19]として知られるアプローチがあり、これはSE崩壊モデルを適用する代わりにSiNCに適用されています[20、21]。このモデルでは、特徴的な遅延時間 t d 、 I としてプロットされた減衰データのピークとして単純に取得されます t ・t 対 t 。これは( 1 と同等であることが示唆されました / β ) 1 / β ・τ SE 式から得られます。 9 [20]。
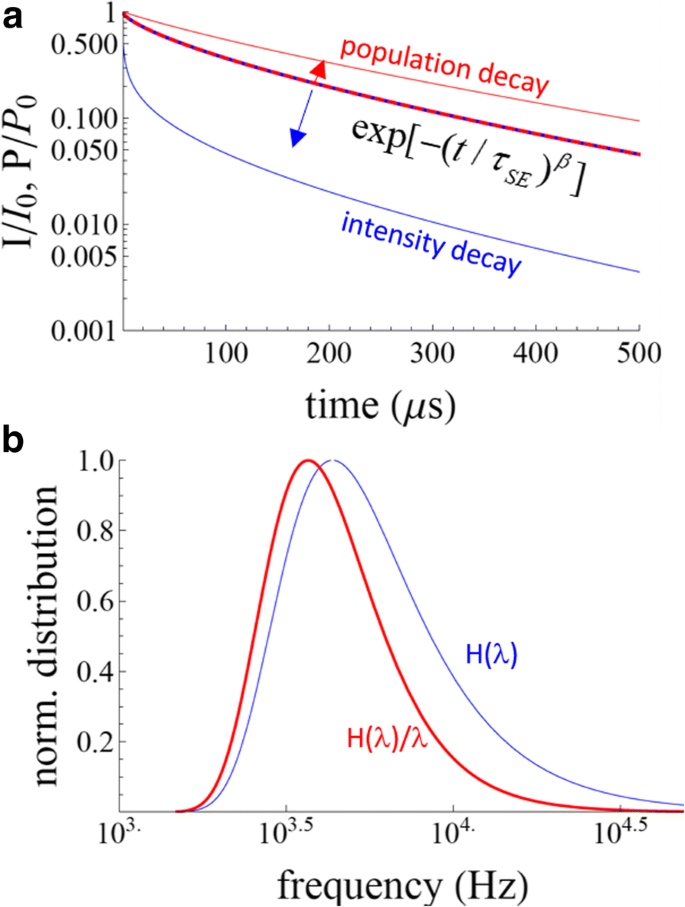
拡張指数。 a τを使用した拡張指数関数の母集団と強度の減衰 SE =100μsおよびβ =0.7。青赤の破線はexp [ − (λt ) β ]。これが人口の減少を表す場合、強度の減少は青い線で示されます。 exp [ − の場合 (λt ) β ]は強度の減衰であり、人口の減衰は赤い線で示されます。 b 対応するレート分布
あるいは、減衰率の分布は特定のΗに従う場合があります (λ )、次の式で発光が減衰します:
$$ g(t)={\ int} _0 ^ {\ infty} \ mathrm {H} \ left(\ lambda \ right)\ cdot \ exp \ left(-\ lambda t \ right)\ mathrm {d} \ラムダ、$$(14)ここでΗ (λ )は、減衰率の周波数依存分布を表します。式14は式になります。 2 Ηの場合 (λ )はディラックのデルタ関数δに等しい ( λ−λ 0 )、または選択した分布によって重み付けされた一連の指数を表すことができます。多くのナノクリスタルアンサンブルは自然に対数正規サイズ分布に従うため、対数正規関数はナノクリスタルシステムでは妥当な選択のようです[22]。さらなる混乱を避けるために、次の式で与えられる対数正規関数の標準正規化定義を使用します。
$$ H \ left(\ lambda \ right)=\ frac {1} {\ lambda} \ cdot \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp \ left [-\ frac {{\ left(\ ln \ lambda- \ mu \ right)} ^ 2} {2 {\ sigma} ^ 2} \ right]。 $$(15)測定された減衰関数が
になるように $$ {I} _t =A \ cdot {\ int} _0 ^ {\ infty} \ left(\ frac {1} {\ lambda} \ cdot \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp \ left [-\ frac {{\ left(\ ln \ lambda- \ mu \ right)} ^ 2} {2 {\ sigma} ^ 2} \ right] \ cdot \ exp \ left(-\ lambda t \ right)d \ lambda \ right)+ dc。 $$(16)SE関数と同様に、2つの独立変数(およびオフセットとスケーリング係数)のみがあります。瞬間はいつものように定義されます。つまり、中央値は exp で与えられます (μ )、 exp による平均 (μ + σ 2 / 2)であり、最も可能性の高い寿命(分布のピーク)は exp です。 (μ − σ 2 )。以前は、非標準分布が採用されていました[16](つまり、それ自体は有効ですが、一般的に受け入れられている対数正規分布関数ではない分布)。式14は、放射性崩壊分布にも適用されます(つまり、AQY =100%)。実際、崩壊率分布は(未知の)量子効率関数によって重み付けされることが示唆されています[16]。実際の状況では、サンプル内の非放射率の人口分布を知ることは困難または不可能であるため、この警告を受け入れる必要があります。
発光の減衰は、2次反応(つまり、「二分子」の減衰)にも対応する可能性があります[23]。ここで、人口が減少する速度は dc で与えられます。 / dt =− λ [ c t ] 2 、残りの分数 c を生成します t / c 0 =( c 0 λt + 1) -1 。この式を式に挿入します。 1はべき乗則の減衰をもたらします:
$$ {I} _t / {I} _0 =A \ frac {\ lambda {c} _0} {{\ left(\ lambda {c} _0 + 1 \ right)} ^ 2}。 $$(17)二分子モデルの速度定数は1つだけですλ (レートの分布を持つ拡張指数および対数正規分布とは異なり)、平均寿命はありません。より具体的には、時間積分は発散し、2次減衰の平均寿命は無限大です。
「標準」SE関数(式9)は、SiNC発光減衰に使用される圧倒的に支配的なモデルであり、多くの論文が発光メカニズムの減衰の意味を解釈することに専念しています。対数正規寿命分布は、ごく最近になってSiNCに最初に適用されました[17、24、25]。明らかに、モデルを想定する先験的な理由はほとんどなく、代わりに減衰率の分布を直接確立することが望ましいでしょう。これは、原則として、少なくとも、直交周波数分解分光法(QFRS)によって達成できます。これは、アモルファスシリコンには何度か適用されていますが、SiNCには適用されていません。
直交周波数分解分光法
QFRS法は、文献ではかなりまばらに報告されており、主に希土類ドープガラスのいくつかの研究に限定されています[26、27、およびa-SiOx:H
直交FRS信号は、単一の指数関数的減衰がQFRSスペクトルのデルタ関数をもたらさないという事実によって複雑になります。観測された信号は、実際には、[31]によって対数スケールで与えられた単一の指数応答関数による寿命分布の畳み込みです。
$$ {S} _ {\ log_ {10} \ mathrm {r}} =\ frac {{\ omega \ tau} _0} {1+ {\ omega} ^ 2 {\ tau} _0 ^ 2}、$$ (18)時定数τ 0 =ω 0 -1 。したがって、減衰率の分布が数十年幅でない限り、意味のある分布を抽出するには、デコンボリューションを実行する必要があります。
結果と考察
基本的な特性評価
SiNCに関連するコントラストが低く、アモルファスカーボンサポートからのまだらのコントラストが重なっているため、明視野画像を使用したコンピューターベースの粒子カウントアルゴリズムは適用できず、ピクセルカウントソフトウェアを使用して「目で」直径を推定する必要がありました(サンプルの明視野TEM画像を図2a、dに示し、手動の粒子カウント結果を対数正規分布(図2c、f)に適合させて、2.9 nmの線形平均直径(の平均および標準偏差)を取得しました。自然対数μ =1.057およびσ=0.1555)および5.4 nm(μ =1.663およびσ=0.1917)、それぞれ1100および1200°Cのアニーリング温度。これらのサンプルは、今後「小」および「大」SiNCと呼ばれます。サイズは、選択されたNCの高解像度イメージングによってさらにチェックされ(図2b、e)、NCを識別し、それらの直径を推定する別の方法として格子縞を使用できます。フーリエ変換赤外(FTIR)分光法とXPSデータは、調製されたSiNCがドデセンで正常に機能化されたことを示しました。ただし、小さいSiNCは大きいSiNCよりも酸化されているため、機能化の程度は低くなります(追加ファイル1:図S1およびS2)。
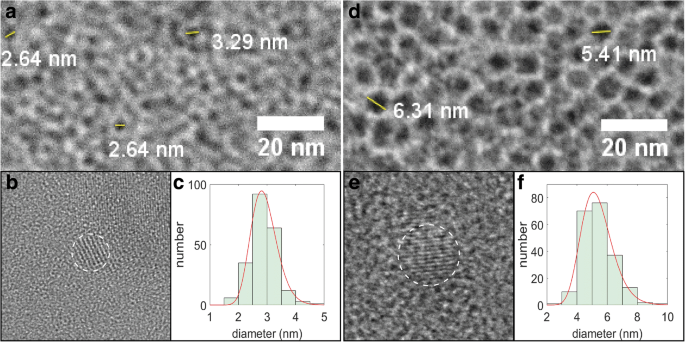
SiNCのTEM画像。 a 明視野、 b 高解像度、および c 小さなSiNCのサイズ分布ヒストグラム。パネル d – f 大規模なSiNCからの同様の画像セットを表す
フォトルミネッセンスと時間分解分光法
フォトルミネッセンス(PL)スペクトルは、660nmと825nmを中心とし、半値全幅は、小さいSiNCと大きいSiNCでそれぞれ123nmと198nmでした(図3挿入図)。間接バンドギャップエネルギーは、\({E} _g \ kern0.5em =\ kern0.5em \ sqrt {E_ {g、\ mathrm {bulk}} ^ 2 \ kern0.5em + \によると、1.87および1.37eVであると予測されます。 kern0.5em D / {R} ^ 2} \)[32] with D =4.8eV 2 / nm 2 および R はNC半径であり、小さな粒子ではほぼ一致していますが、大きな粒子のPLピークで得られるバンドギャップよりもわずかに小さいバンドギャップを予測しています。 AQYは、小さいSiNCサンプルで12%、大きいNCで56%でした。異なるシステムでの独立した測定では、2つのサンプルで18%と48%が得られました。これは、異なる励起波長とカットオフ波長でのAQY測定[33]の不確実性の典型です。大きなNCの湾曲が少なく、エネルギーの低い表面は、表面の機能化が向上し、非放射表面状態からPLスペクトル全体への寄与が小さくなると仮定します。
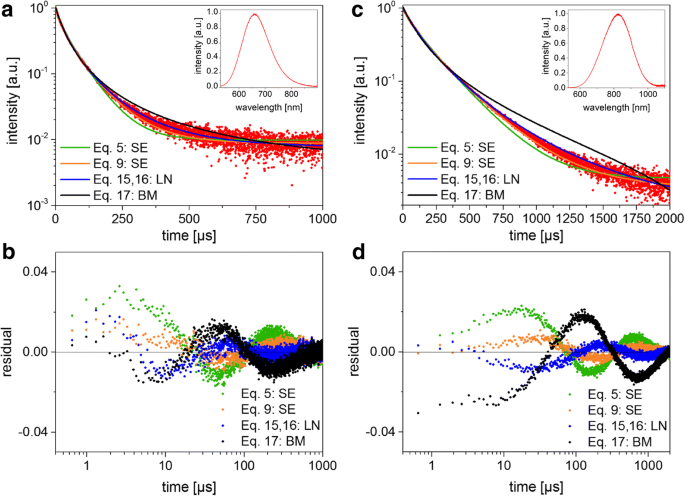
TRSデータとフィッティング結果。 a 発光減衰と対応するフィッティング関数( BM 二分子、 SE 拡張指数、 LN 対数正規)小さいSiNCの場合。 PLスペクトルは挿入図に示されています。 b ( a の適合の残差プロット 、 c 、 d )大きなSiNCの曲線と残差を示します。
SiNCに関する以前の広範な文献に基づいて予想されたように、両方のサンプルは非指数関数的減衰をもたらしました。測定されたPL減衰は、式に適合しました。標準の二乗和最小化を使用してさまざまなモデルをテストするための5、9、16、および17(図3)。検出器の応答性が広いNC発光スペクトルにわたって一定ではないという事実については、後で説明します。すべての場合において、残差は振動し、どのモデルも完全に適切に見えないことを示しますが、「単純な」SEモデル(式9)と対数正規(式16)は、残差の二乗和が最小になる傾向があります。 2つのSiNCサンプルの計算されたフィッティングパラメータと平均寿命を表2に示します。この表では、平均が減衰モデルの選択に明らかに依存しています。 Higashi-Kastner法も適用され(図4)、遅延時間曲線を歪んだガウス分布でフィッティングすることによってピーク位置が決定されました。 Higashi-Kastner法では、時定数 t が得られます。 d ( 1 と非常によく似ています / β ) 1 / β ∙τ SE 、これらの値は式から取得します。 [20]の前に示したように9。二分子モデルはかなり不十分に適合し、過度に励起されていない孤立したナノ結晶と一致しています。したがって、これ以上は説明しません。
<図>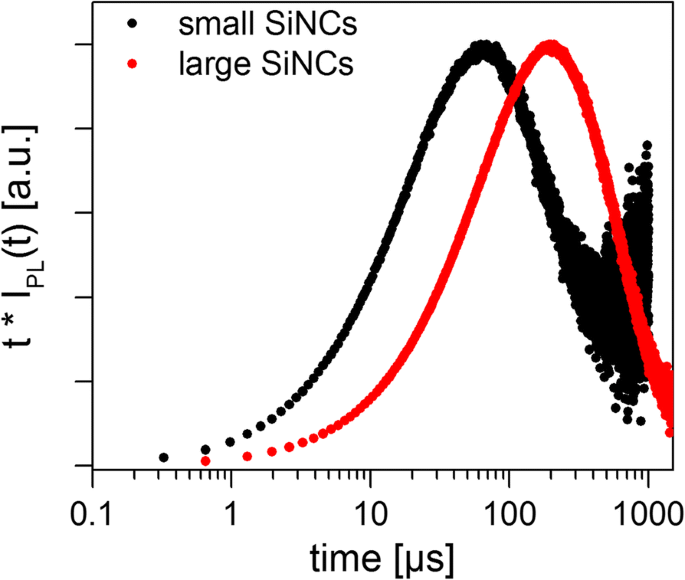
正規化されたPL減衰曲線に、大小のSiNCアンサンブルの減衰時間(Higashi-Kastnerプロット)を掛けたもの。ピーク位置は、 t で表される最も支配的な減衰時間を表します d 表2
これらの測定条件でNCあたりの平均励起子数を推定するには、吸収断面積から励起子率を計算する必要があります。これは明らかに10 -14 に達する可能性があります。 cm 2 これらの実験のために[34]。 4500 W / m 2 の励起放射照度が与えられた場合 352 nmおよび測定されたピーク発光率(次のセクションを参照)では、大小のSiNCのNCあたりの励起数は、それぞれ〜1および0.2未満であると推定されました。これは、大きなSiNCがわずかに過剰に励起されている可能性があることを示しています。これは、一部のNCに多重励起子が存在するため、追加の非放射効果を引き起こす可能性があります。この可能性をさらに評価するために、寿命を励起パワーの関数として測定しました。上記で報告された値の2%まで。結果は傾向を示さず、〜2%以内で常に同じでした(追加ファイル1図S3)。これは、低電力測定での信号対雑音比が低いにもかかわらず、フィッティングと再現性のエラーに近い値です。したがって、NCの過剰励起の可能性は、結果にほとんど影響を与えないようです。
TRSから寿命分布を推定するために、約3 nmのバンドパスを備えたモノクロメーターを使用して、一連の固定波長にわたって減衰を測定しました(図5)。強度が低いため、この目的のためにフォトンカウンティングPMTシステムが使用されました。効果的に単色光を使用する場合、このような狭い波長範囲での応答関数の分布はごくわずかであるため、さまざまな検出器で測定された減衰定数に違いはありません。他のシリコンNCで観察されたのと同じ傾向がドデシル末端粒子にも見られました[25、35、36]。つまり、分散パラメータは1に近づくにつれて増加し、寿命は波長の関数として急速に増加します(図5、表3)。
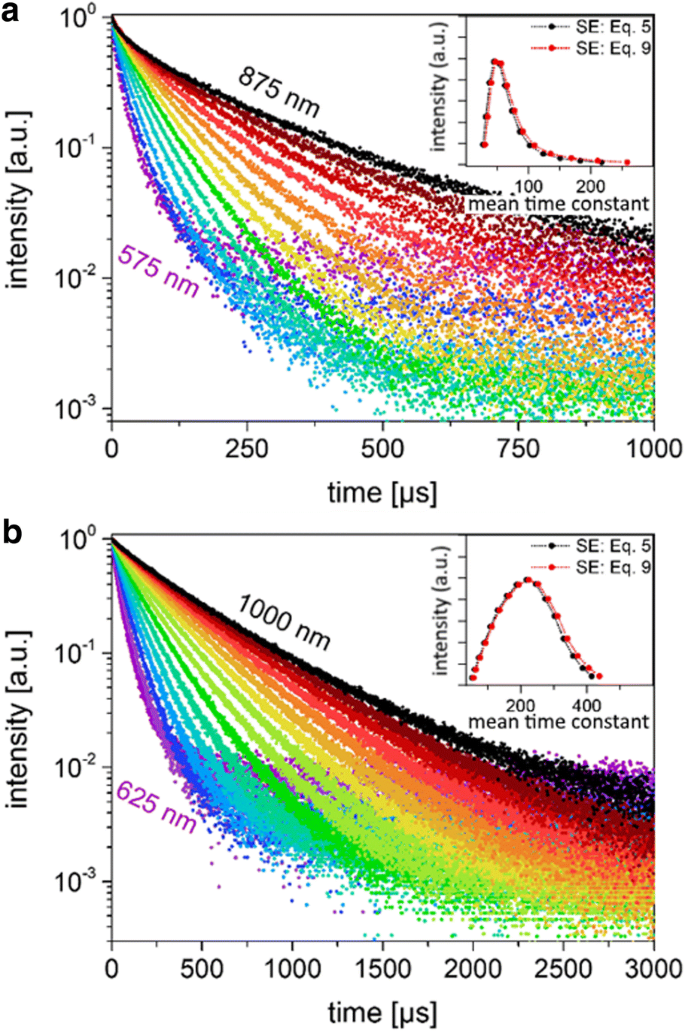
狭波長PLは減衰します。 a 小さなSiNCの発光は、25 nm間隔で575〜875 nmの範囲の特定の発光波長(3 nm FWHM)で減衰します。データは式に適合しました。 5と9は、ほぼ単一の指数フィットをもたらしました。 b 同じ条件下で測定および適合された大型SiNCの場合、発光は625〜1000nmの範囲の特定の発光波長で減衰します。小さいSiNCと大きいSiNCの結果の時定数を表1に示します
小さい粒子は、同じ測定波長で大きい粒子よりも常に寿命が短くなりました。この観察結果は、小さい粒子のAQYが低いことと一致しており、大きいNCの寿命が非放射プロセスによってあまり強く支配されていないことを示しています。大きなNCは、小さなNCサンプルと比較して酸化も少ないです(追加ファイル1図S1)。したがって、小さなサンプルでの低いAQYの観測は、測定された短い寿命と一致しますが、波長の選択によって2つのサンプルの相対的な比較を行うことはできません(基本的に、発光波長はサイズと> 酸化の程度[24]、これは2つのサンプルで異なります。
また、図5の挿入図としてプロットされているのは、単色化されたデータから得られた平均寿命を式(1)を使用してプロットすることによって得られた分布です。その波長でのPL強度の関数として、データを適合させるために5または9。これらの減衰の場合、ベータパラメータは1にかなり近いため、SEモデルの2つのバージョンで計算された平均寿命の間にほとんど違いはなく、この方法で得られた分布は類似しているように見えます。これらの崩壊は、 I への非放射性の寄与による、寿命の「真の」分布を表すものではありませんが PL 、それにもかかわらず、それらは寿命分布の指標を与えることができます。小さな粒子の場合、〜47μsにピークが観察されますが、大きなNCの場合、ピークはより対称的で、220μsを中心にしています。
周波数分解分光法
まず、2つのテスト標準からのFRSデータを検証しました。1つ目はRC回路で、2つ目は蛍光Euキレートドープミクロスフェア(Fisher Scientific)のサンプルでした。 RC回路には、FRSデータが式(1)と一致する単指数関数的減衰があります。 9は非常に近く、12.7 kHzでピークに達し、測定された減衰時定数78.9μsと一致しています。 Eu-キレートPLスペクトルは、650 nmでピークに達し、減衰時間は数百マイクロ秒のオーダーであり、SiNCの標準を示しています。発光はまた、670μsの寿命でほぼ単指数関数的に減衰しました。 FRSデータは約1570Hzを中心とし、幅は応答関数(Eq。18)に実質的に等しく、これは観測されたTRSの結果にかなり近いものです。違い(636対670μs)は、以下でさらに説明するように、励起法に結合された減衰のわずかに非指数関数的な振る舞いに起因する可能性があります。
Si-NCのFRSデータは、観測されたQFRSの結果が応答関数よりもわずかに広いことが判明したため、問題があります(図6aの挿入図を参照)。したがって、データに対してデコンボリューションを実行する必要があります。デコンボリューション手順の重大な問題を回避するには、データにノイズがほとんどない必要があります。陽性制約を適用するために、リチャードソン-ルーシーデコンボリューション法[37]を使用しました。次に、デコンボリューションおよび正規化されたQFRSデータは、モデルを事前に想定せずに、それぞれ大および小NC(赤い点)について図6に示すように、測定された寿命分布を直接生成します。両方のサンプルで、片対数プロットでは小さいNC分布がより対称的であるのに対し、大きいNCの場合は、より高い周波数に向かってわずかに歪んでいる広い寿命分布が見つかります。減衰率の分布は、小さいNCでは19,900 Hz(50.3μs)でピークに達しましたが、大きいNCでは6280 Hz(159.2μs)でピークになりました。
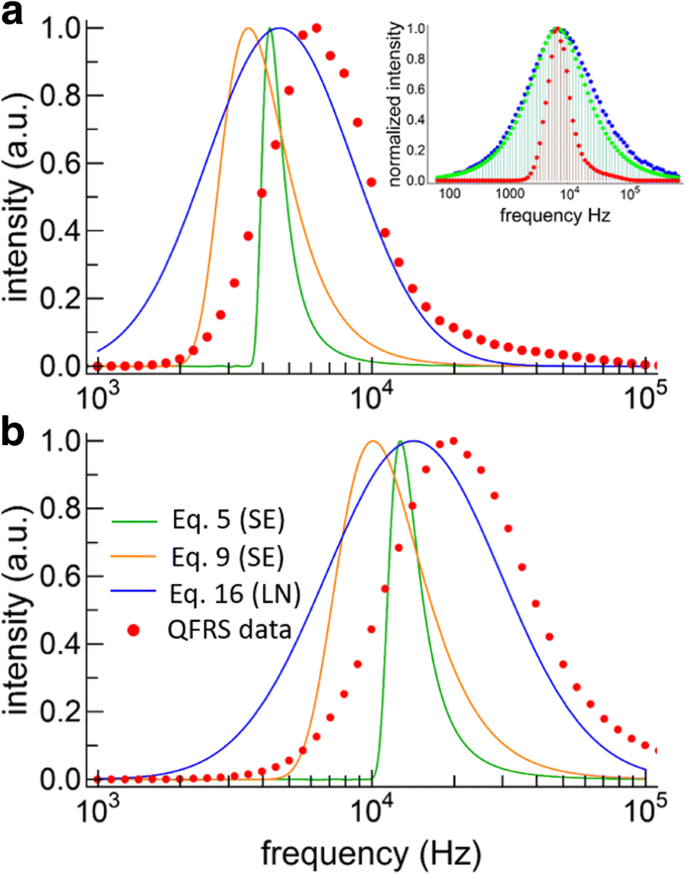
生涯分布。 a TRSデータを2つのSEモデルとLNモデルに適合させて得られた大型SiNCの寿命分布。デコンボリューションされたQFRSデータも表示されます(赤い点)。挿入図は、このサンプルの生のQFRSデータ(青)、応答関数(緑)、およびデコンボリューション(赤)を示しています。 b 小さなSiNCのTRSデータ(線、両方のグラフで同じ配色)とQFRS(赤い点)をモデルフィッティングすることによって得られた寿命分布
拡張指数(オレンジと緑の曲線)と対数正規(青の曲線)モデルの適合から得られた寿命分布も、大粒子と小粒子について図6にプロットされています。 3つの減衰モデルは、全体的な形状とピーク頻度の両方の点で異なる分布を生成します。どちらのサンプルでも、QFRSは、どのTRSモデルよりも高い周波数でピークに達します。これは意外に思われるかもしれませんが、寿命の分布を持つCdSe NCでも同じ効果が観察されています[38、39]。実際、CdSe NCのTRS減衰曲線は明らかにパルス幅に敏感であり、パルスが短いほど寿命が短くなり、パルスが長い場合は逆になります。さらに、長パルス持続時間技術によって得られた平均寿命は、位相測定によって得られたものの3〜4倍長かった。これは、定常状態の励起における長寿命集団の優先的な励起によるものであった[38]。実際、繰り返し率が遅いTRSの応答関数は、FRSの応答関数よりも狭く、高周波側で特に急激に遮断されます[29]。基本的に、FRSは、定常状態のTRSよりもアンサンブル減衰の短命成分を強調します。これは、TRSモデルフィッティングとFRSによって得られるピーク周波数の違いを説明している可能性があります。これらの固有の違いにもかかわらず、FRSは、想定されたモデルではなく直接測定によって取得されるため、SiNCのアンサンブルの寿命の分布を明らかにするのに適しているように見えます。熱的に成長したアンサンブルに典型的なSiNCの場合、FRSの主な欠点はデコンボリューションの必要性です。
検出器の応答関数は確かにQFRSに影響を与えますが、TRSデータでも役割を果たします。実際、APDとPMTの設定でアンサンブルの減衰を測定すると、適用されたフィッティングモデルに関係なく、平均減衰時間が約2倍異なりました。検出器の応答性は、TRSの「最適な」モデルの選択にも影響します。前述のように、当社の当社のAPD応答性は600 nmでピークに達しますが、浜松PMTの場合、応答性はSiNCスペクトルの長波長でゆっくりと減衰する部分で850nmで最大になります。 SiNCに関する文献ではこれまで報告されていないようですが、この問題は、さまざまな設定からの広域スペクトルTRSの結果を比較できないことを意味します。残念ながら、いくつかの重要な結論にもかかわらず、ref。 [38]はまた、同じ広帯域NCサンプルからの減衰ダイナミクスを比較するために異なる検出器を使用し、応答関数は同じではなかった可能性があります。ただし、幸いなことに、位相測定と定常状態測定では同じ検出器が使用され(ここでの場合のように)、これらの状況で観測されたダイナミクスの違いは引き続き有効です。最後に、応答曲線と単色化された減衰率の分布が広範囲の波長(つまり、減衰率)にわたってわかっている場合、検出器の応答関数は原則としてFRSデータで修正可能です。応答性の修正には、TRSだけではそのような単純な解決策はありません。
結論
SiNC発光減衰に使用される最も一般的なモデルは理論的に説明されています。 「単純な」拡張指数発光減衰exp [−( t )に対応する母集団減衰 / τ ) β ]が導き出され、特徴的な平均時間の式が見つかりました。このモデルは、単純なSEに従って母集団が減衰する代替モデルと比較されました。次に、2つのドデセン官能化SiNCサンプルを、熱核形成と成長、続いてエッチングとアルカン表面官能化から調製しました。これらのサンプルは、平均直径がそれぞれ2.9nmと5.4nmの粒子で構成されていました。基本的なPLスペクトルとTRSは、標準的な方法を使用して測定されました。 TRSデータは、それらのいずれかが「真」であると見なすことができるかどうかを確認し、どれが最適であるかを見つけるために、いくつかの分布に適合しました。単純なSE発光減衰はTRSデータにかなりよく適合しますが、残差の分布はそれが厳密に正確ではないことを示しています。測定された減衰率分布の形状を完全に捉えているフィッティングモデルはありません。また、ピーク位置と分布の形状に大きな偏差があり、平均時定数に不一致があります。さらに、アンサンブルの平均時定数は、検出システムの応答曲線に依存していました。これは、熱的に成長したSiNCの集合からのPL崩壊をどのように解釈するかについての深刻な疑問につながります。
次に、直交周波数分解分光法を使用して、ベース酸化物の熱アニーリングによって形成されたSiNCアンサンブルの寿命分布を直接見つけることを目的としました。スペクトルは、固有のQFRS応答関数よりもそれほど広くないことがわかり、SiNCレート分布を抽出するためにデコンボリューションが必要です。これにより、小さなNCサンプルでは形状がほぼ対称で(片対数スケールで)、幅が約5年である分布が得られましたが、大きなNCではわずかに歪んでいました。 FRS技術は、SiNC発光ダイナミクスの研究に適しており、データからシステム応答をデコンボリューションした後、FRSは減衰率分布を直接生成します。最も重要な問題は必要なデコンボリューションですが、Richardson-Lucy法はかなり堅牢な結果を生成することがわかりました。検出器の応答関数は原則としてFRSデータから修正できますが、広帯域TRSデータに対してこれを行う簡単な方法はありません。それでも、比較されるデータが同じ検出器からのものである限り、結果は少なくとも内部的に意味のあるものでなければなりません。将来的には、これらの問題は、PLスペクトルで機能する動的プロセスを記述および特性化するために、デフォルトで単純な拡張指数モデル(式9)を使用するのではなく、不均一に広がったNC発光寿命を分析するときにさらに十分に考慮されるでしょう。
メソッド
SiNCは、最近提案された方法[21]に従って合成されました。簡単に説明すると、4 gの水素シルセスキオキサン(HSQ)を、流れる5%H 2 中で1100または1200°Cで1時間アニーリングしました。 + 95%Ar雰囲気、シリカマトリックスに埋め込まれたSiNCの複合材料になります。これらの複合材料は、瑪瑙乳鉢を使用して機械的に微粉末に粉砕されました。手首アクションシェーカーを使用して、粉末をガラスビーズで約8時間振とうした。粉末を95%エタノールに懸濁し、フィルターを備えた真空ろ過システムに接続しました。 H-SiNCを遊離させるために、HFエッチングによってシリカマトリックスを除去しました。複合材料の約200mgのアリコートをテフロンビーカーに移し、そこに2 mLのエタノール、2 mLの水、および2 mLの49%HF水溶液を加えてシリカマトリックスを溶解しました。懸濁液を40分間撹拌した後、遊離したH-SiNCをトルエンを使用して濁った黄色の懸濁液として抽出し、3000rpmで5分間の遠心分離によって単離した。得られた水素終端SiNCを10mLの乾燥トルエンに懸濁し、マグネチックスターラーを備えたオーブン乾燥したシュレンクフラスコに移しました。続いて、1mLの1-ドデセン(約4.6ミリモル)、および20mgのAIBNを加えた。懸濁液は、Ar帯電シュレンクラインを使用して3回の凍結-ポンプ-解凍サイクルにかけられました。懸濁液を室温まで温めた後、70℃で24時間撹拌し、続いて10mLのメタノールと20mLのエタノールを透明な反応混合物に加えた。得られた濁った懸濁液を50mL PTFEバイアルに移し、12,000rpmで20分間遠心分離してSiNCを分離しました。 SiNCを10mLのトルエンに再分散させ、30 mLのエタノール貧溶媒を添加して分離し、さらに遠心分離しました。後者の手順はもう一度実行されました。最後に、ドデシル-SiNCを5 mLの乾燥トルエンに再分散させ、光学研究のためにスクリューキャップ付きバイアル(濃度〜0.5 mg / mL)に保存しました。
TEMサンプルは、自立型ナノ粒子を極薄(約3 nm)のカーボンコーティングされた銅TEMグリッドに直接堆積させることによって準備されました。 NCは、JEOL JEM-2010を使用した明視野TEMによって画像化され、HRTEMはJEOLJEM-ARM200CFで実行されました。フーリエ変換赤外分光法(FTIR)は、ThermoScientificのNicolet8700で実行されました。 X線光電子分光法は、Phoibos 150 2DCCD半球アナライザーとFocus500モノクロメーターを備えたSPECSシステムで測定されました。検出器の角度は表面に対して垂直に設定され、X線源はMgKα線でした。
発光スペクトルは352nm Ar + で励起されました Isomet IMDD-T110 L-1.5音響光学変調器(AOM)を使用して約50 nsの立ち下がり時間でパルス化されたイオンレーザー(50%デューティサイクル、50〜250 Hz)。使用したセットアップを図7に模式的に示します。レーザービームは音響光学変調器を通過し、回折ビームの1つがアイリスによって選択されます。ビームスプリッターは、パルスレーザービームの主要部分をサンプルキュベットに反射し、サンプルへの入射パワーは、〜4 mm 2 の領域に約8mW広がりました。 。発光は光ファイバー(開口数0.22)で収集され、450 nmのロングパスフィルターを通過し、適切な検出器に導かれます。 PLスペクトルは、Ocean Opticsミニチュア分光計によって測定され、その応答関数は、校正された放射線源(OceanOpticsのHL-3 + -CAL)を使用して補正されました。量子効率は、405 nmの励起を伴う積分球を使用し、その波長で約0.15の吸光度を持つように希釈された溶液を使用して測定されました。
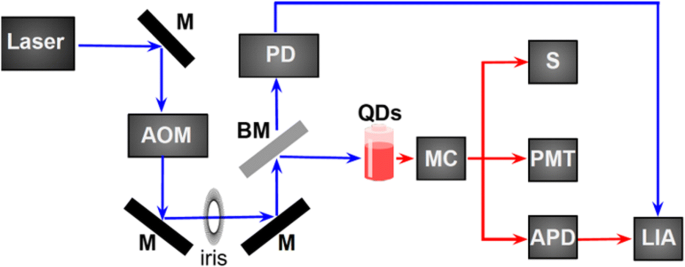
実験装置の図。 M ミラー、 AOM 音響光学変調器、 BM ビームスプリッター、 PD フォトダイオード、 MC モノクロメータ、 S 分光計、 PMT 光電子増倍管、 APD アバランシェフォトダイオード、 LIA ロックインアンプ
発光ダイナミクスは、2つの異なる検出器で測定されました。最初の検出器は、デジタルオシロスコープモードでMoku:Lab(200 MHz)に接続されたThorlabs 120A2アバランシェフォトダイオード(50 MHzロールオフ)でした。 2番目の検出器は、Becker-HicklPMS400マルチスケーラーに接続されたHamamatsuh7422-50光電子増倍管でした。発光減衰時間の誤差は、測定を3回繰り返すことによって得られ、1μsの拡張指数フィット(式4)を使用して計算された平均寿命の標準誤差が得られました。減衰データへのすべての適合は、Levenberg-Marquardtアルゴリズムを使用した最小二乗法を使用してOriginで行われ、同じ方法を使用してMatlabで繰り返されました。波長依存の減衰測定では、検出前に、検出された放射線の半値幅を約3nmに設定して発光をActonMS2500iモノクロメーターに送信しました。
QFRS測定では、AOMは正弦波振動を生成するように設定されました。入射ビームの一部は、基準信号を生成するために、当社のPDA10Aフォトダイオード(200 MHz)に偏向されました。 SiNC PL応答は同時に収集され、APDに送信されました。参照信号はビームスプリッターを使用して取得し、対応するPL信号とともに、ロックインアンプモードのMoku:Labを使用して分析し、信号の同相成分と直交成分を測定しました。
最後に、以前に報告され、酸化に起因することがあるように、発光の短寿命成分も検索しました[22]。このシステムは、405 nmピコ秒ダイオードレーザー(Alphalas GmbH)を使用してNCを励起し、Becker-Hickl HPM-100-50PMTをSPC-130パルスカウンターシステムに接続しました。このセットアップの応答時間は〜100psです。これらのSiNCではナノ秒の減衰の証拠は観察されませんでした。
略語
- APD:
-
アバランシェフォトダイオード
- AQY:
-
絶対量子収率
- FRS:
-
周波数分解分光法
- LN:
-
対数正規
- NC:
-
ナノクリスタル
- PL:
-
フォトルミネッセンス
- PMT:
-
光電子増倍管
- QFRS:
-
直交周波数分解分光法
- SE:
-
拡張指数
- SiNC:
-
シリコンナノ結晶
- TRS:
-
時間分解分光法
ナノマテリアル



