水素化グラフェン/六方晶窒化ホウ素ヘテロ二層のキャリア移動度に関する理論的研究

はじめに

水素化グラフェン（HG）[1、2]は、最も有望なグラフェンベースの材料の1つです。水素貯蔵[3]、強磁性[4]、蛍光[5]、熱整流[6]などの広範な用途により、広く注目を集めています。金属グラフェンとは対照的に、HGは調整可能なバンドギャップを持つ半導体であると予測されています[7、8]。したがって、電界効果トランジスタ（FET）のチャネル材料として使用できます[9]。優れたFETは、チャネル材料の超高キャリア移動度を備えている必要があります。よく知られているように、従来のSiO ₂ 基板はFETの性能に重大な悪影響を及ぼします[10]。最近の研究では、単層の六方晶窒化ホウ素（h-BN）[11、12]がグラフェンベースのFETの基板の有望な候補であることが示されています。単分子層のh-BNとHGは格子整合構造であり、接触性能が優れていることを示しています。したがって、HG / h-BNヘテロ二重層はFETのチャネルの理想的な構造です。残念ながら、HG / h-BNヘテロ二層構造の電子特性に関する関連研究はわずかしかありません。 HG / h-BNヘテロ二層のキャリア移動度性能は未解決の問題です。

HGに関する現在の研究のほとんどは、水素化を介して目的の電子特性を設計することに専念しています[13、14、15、16、17、18]。 Gao etal。 [13]は、HGのバンドギャップの水素被覆率と構成依存性を研究しました。 Sahin etal。 [14]は、バンド構造に対する吸着原子パターン（水素化）と穴パターン（炭素原子の除去）のグラフェンナノメッシュの効果を比較しました。 Shkrebtii etal。 [15]は、HGのバンド構造を調査しました。HGの構造はC ₁₆ で制限されています。 H _n システム（ n =0,2,8,16）。 Song etal。 [16]は、六角形の空孔が異なるHGのバンドギャップを計算しました。 Bruzzone etal。 [17]は、ab-initioシミュレーションによって異なる水素被覆率（100％、75％、25％）でHGの移動度を計算し、25％HGが最高の移動度を取得したことを発見しました。 h-BNに水素化を適用することについてのいくつかの研究もあります。 Chen etal。 [19]は水素化を利用して、h-BNにおける半導体から金属への転移を実現しました。 Liang etal。 [20]は、100％HGと100％水素化h-BNの間の相互作用を研究しました。 HG /水素化h-BNの電子移動度はわずか50cm ² であることを示しています。 /（V s）これはグラフェンのそれから遠く離れています。

一言で言えば、HG / h-BNヘテロ二層のキャリア移動度に関する現在の研究はまだ十分ではありません。 HG / h-BNヘテロ二重層のキャリア移動度に影響を与える主な要因、すなわち水素被覆率、水素化パターン、およびHGとh-BN間のスタッキングパターンを明らかにする必要があります。本論文では、第一原理計算に基づいて、HG / h-BNヘテロ二層構造のキャリア移動度を調査した。最初に、HGの移動度に対するh-BN基質の影響を調べた。次に、水素被覆率が異なるHGの電子特性を比較しました。最後に、異なる水素化パターンを25％と6.25％のHGで適用して、水素化パターンの影響を明らかにしました。

メソッド

すべての計算は、密度汎関数理論（DFT）に基づいてAtomistix ToolKit（ATK）[21]で実装されました。交換相関は、Perdew-Burke-Ernzerhof（PBE）汎関数を使用した一般化勾配近似（GGA）です。ファンデルワールス（vdW）補正は、ヘテロ二層構造にGrimmeDFT-D2法[22]を採用しました。 z のセルの長さ 周期的な画像の影響を排除するために、方向（HG平面に垂直）は20Åです。 k点サンプリングは33×33×1Monkhorst-Packグリッドです。

変形ポテンシャル近似（DPA）法[23]は、キャリア移動度を調査するために使用されます。 2D材料のキャリア移動度の表現[24、25]は次のとおりです。

ここで e は電子電荷、ћ プランク定数、 k が減少します _B ボルツマン定数、 T は温度（この場合は300 Kに設定されています）であり、 C _2D は伝播方向の弾性率です。 E ₁ E で定義される変形ポテンシャル定数です。 ₁ =Δ V /（Δ l / l ₀ ）。 Δ V 適切な細胞の圧縮と拡張の下でのエネルギー変化です。伝導帯の最小値（CBM）の変化は電子に使用され、価電子帯の最大値（VBM）は正孔に使用されます。 l ₀ は輸送方向の格子長であり、Δ l はその変形です（Δ l / l ₀ は− 0.01、− 0.005、0、0.005、0.01に設定されます。 m ^* は、輸送方向の有効質量であり、次の式で計算されます。

ここで k は波数ベクトルであり、 E エネルギーです。 m _d は、 m として定義される等価状態密度質量です。 _d =（ m _x m _y ） ^0.5 。変形ポテンシャル定数と有効質量はバンド構造から推定でき、弾性率はフォノン分散関係から抽出されます。 DPA法は、曲げ音響（ZA）フォノンの影響を考慮していないため、アルセネン、アンチモネン[26]、およびシリセン[27]の移動度を過大評価する可能性があることを強調しておく必要があります。 Shuai etal。 [28、29]は、DPAの適用性について議論し、グラフェンとグラフェンの電子特性をうまく推定できることを発見しました。 ZAフォノンは、2次元炭素材料の電子-フォノン相互作用において小さな役割を果たします。室温でのグラフェンの電子移動度[28]は、3.4×10 ⁵ と推定されます。 cm ² /（V s）DPA法および3.2×10 ⁵ cm ² /（V s）[28]すべての電子-フォノン相互作用を考慮します。 HGについては、次のパートでZAフォノンの効果を再分析します。

結果と考察

最初に、HGが100％水素化されているh-BNとHGの間の異なるスタッキングパターンが調査されました。 HGとh-BNの間の相互作用はvdW力であり、共有結合よりもはるかに弱いことを強調しておく必要があります。したがって、他のHG / h-BNヘテロ二重層を分析する必要はありません。図1a〜dに示すように、ヘテロ二層には4つの可能なスタッキングパターンがあります。ここで、「 a 」は格子定数であり、「 d 」は層間距離です。層間距離は、図1aに示すように、HG層とh-BN層の幾何学的中心間の距離として定義されます。パターンIとIIでは、2つのスケルトンはAAスタッキングにあり、パターンIIIとIVではABスタッキングにあります。構造は、最初にLBFGSオプティマイザー法によってジオメトリ最適化されました。力の許容範囲の収束基準は0.001eV /Å未満です。ジオメトリの最適化後、ユニットセルパラメータはすべてのスタッキングパターンで2.52Åですが、層間距離はスタッキングパターンによって異なります。パターンIの層間距離が最も短く、パターンIIIが最も高くなります。 4つのパターンのvdW補正は、それぞれ− 651.69 meV、− 658.14 meV、− 658.22 meV、および− 651.54meVです。明らかに、vdW相互作用の傾向は層間距離の傾向と一致します。

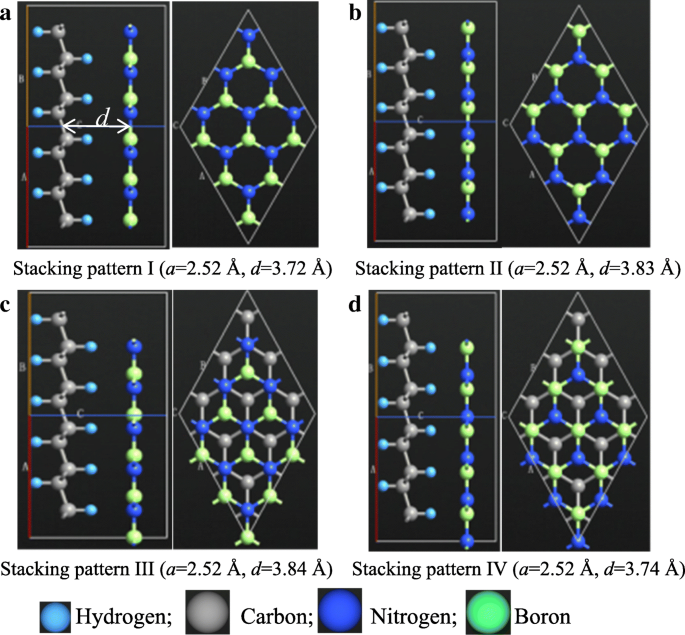
a – d 100％-HG / h-BNヘテロ二層の可能なスタッキングパターン

バンド構造は、最も重要な電子特性の1つです。スタッキングパターンI〜IVの対応するバンド構造を図2に示します。各図の2つの太線は、それぞれCBM（上）とVBM（下）を含むバンドを表しています。 Γ（0,0,0）、M（0,0.5,0）、K（0.333,0.333,0）は、ブリルアンゾーンの対称点です。直接バンドギャップ（DBG）、間接バンドギャップ（IBG）、CBM、およびVBMの位置を含むメインバンド構造情報に注意する必要があります。一般的に、4つのパターンは同様のバンド構造を持っています。パターンI〜IVの場合、CBMとVBMはそれぞれポイントKとΓにあります。パターンIとIVのDBG（4.35 eV）とIBG（3.25 eV）は類似していますが、パターンIIとIIIのDBGとIBGは約4.22eVと2.98eVです。それらの層間距離を比較することにより、より強い層間相互作用がより広いバンドギャップにつながると結論付けることができる。単層h-BNのバンド構造もPBEで計算されることを強調しておく必要があります。 h-BNのバンドギャップは4.65eVであり、[30]で報告されている値とよく一致しています。全体として、この方法はh-BNに適しています。

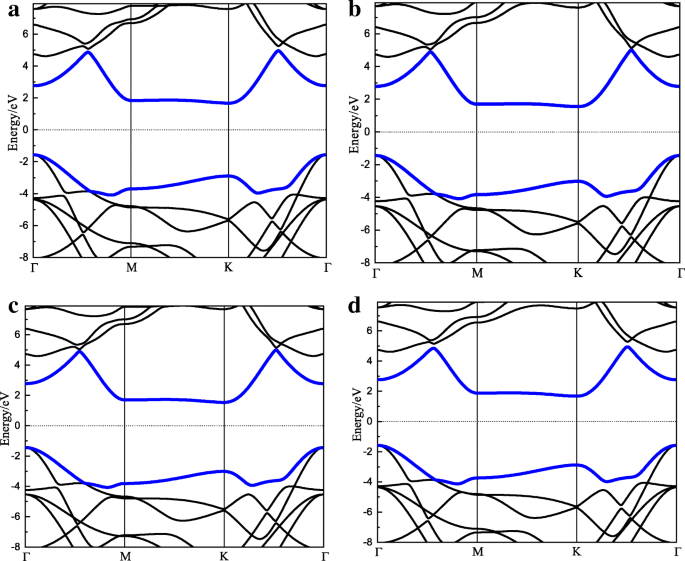
a – d 100％-HG / h-BNヘテロ二層スタッキングパターンI–IVのバンド構造

次に、水素被覆率と水素化パターンの影響が考慮されますが、水素化の影響は、vdW力よりもはるかに強い共有結合の変化に起因します。したがって、この部分ではHG単層のみを調査します。検討した構造を図3に示します。ここで、「 "および" "は、さまざまな側で水素原子と結合している炭素原子を示します。構造全体の安定性のために、水素原子は両側に均等に分布しています。 100％HGの場合、安定したパターンは1つだけです。 8Cと2Hで構成される25パーセントのHGには、3つの異なるパターンがあります。 6.25％HGの場合、プリミティブセルに32Cと2Hがあります。 6.25％HGの2つのパターンのみが考慮されます。図３ｂ、ｃに示されるように、２つの水素化炭素原子は、パターンＩでは互いに隣接し、パターンＩＩでは互いに離れている。 6.25％のパターンI、25％のパターンI、および100％のHGが同じタイプであることに注意してください（2つの水素化炭素原子が隣接しています）。図3では、 E _f は原子あたりの形成エネルギーです

ここで E _合計 はHGの総エネルギー、 E _{グラフェン} 純粋なグラフェンのエネルギーを指します E _H はH ₂ の原子あたりのエネルギーです 分子、および n _H は吸着された水素原子の数です。 E _f 構造の安定性をチェックするために使用され、負の E _f 熱力学の安定性を示唆しています。図3の結果は、リストされているすべてのHGが安定していることを示しています。 η は、グラフェンとは対照的なHGの格子定数の上昇率を示します（グラフェンの最小単位セル長は2.47Åです）。全体として、格子の強化は水素被覆率の減少とともに減少します。 6.25％HGの場合、η ほとんど無視できます。水素被覆率に加えて、水素化パターンも格子に影響を与えます。 25％HGの場合、主に水素化炭素原子が隣接しているため、パターンIは3つのパターンの中で最も大きく拡大していません。 Δ は座屈パラメータであり、炭素原子の面外変位の標準偏差として定義されます。一般に、座屈パラメータは水素被覆率の増加とともに増加します。

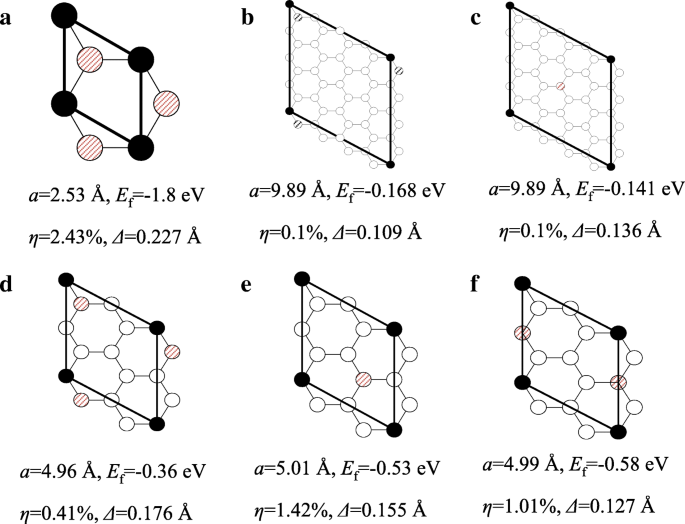
水素被覆率とパターンが異なるHGの原始細胞の概略図。 a 100％。 b 、 c 6.25％パターンIおよびII。 d 、 f 25％パターンI–III

上記のHGのバンド構造を図4に示します。100％HGのバンドギャップは約4.14 eVであり、以前の文献[16、31]とよく一致しています。 25％HGの場合、バンドギャップは水素化パターンの影響を強く受けます。パターンIIのIBGは3.0eVですが、パターンIIIのIBGは0eVです。ゼロから非ゼロへのIBGは、金属から半導体への遷移を示します。さらに、パターンIIには異なるDBGとIBGがあり、そのCBMとVBMが異なるポイントにあることを示唆しています。 6.25％HGの場合、VBMとCBMは、2つのパターンの両方で同じポイントにあります。パターンIは（0.153、0.423、0）で、パターンIIは（0.24、0.24、0）です。 2つの6.25％HGのバンドギャップは0eVと0.49eVであり、どちらも100％HGのバンドギャップとは対照的に大幅に減少しています。一般に、水素被覆率と水素化パターンの両方が、バンドギャップを調整するための効果的な方法です。

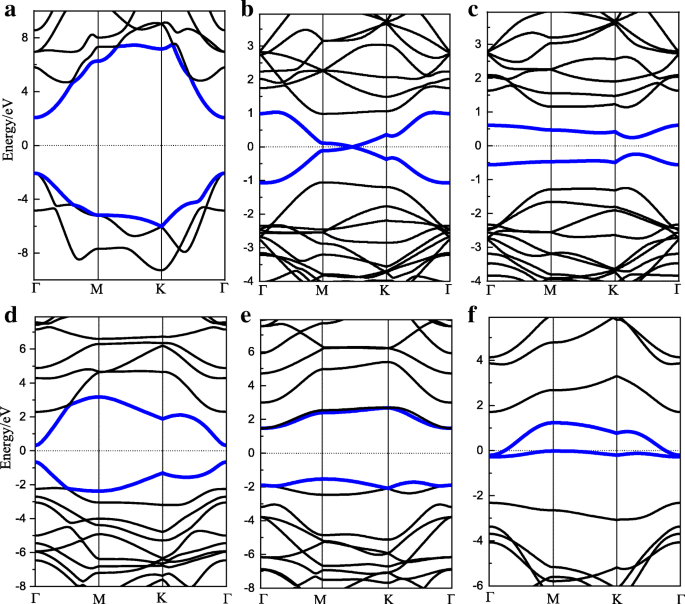
HGのバンド構造。 a 100％。 b 、 c 6.25％パターンIおよびII。 d 、 f 25％パターンI–III

表1に、弾性率 C の推定値を示します。 _2D 、有効質量 m ^* および変形ポテンシャル定数 E ₁ 。 C _2D および m ^* 方向に依存するパラメータです。すべての方向の中で、ΓMとΓKが最も懸念されます。したがって、 C _2D （ΓM/ΓK）および m *（ΓM/ΓK）を表1に示します。 C _2D =ρv _g ² 、ここでρ は密度であり、 v _g 音響フォノンの群速度を示します。水素化は群速度にほとんど影響を与えないため、 C _2D 異なるHGのは互いに類似しています。 HG v _g は、ΓK方向で約23 km / s、ΓMで19.4 km / sであるため、 C _2D （ΓK）は C よりはるかに高い _2D （ΓM）。変形ポテンシャル定数は、パターンが異なると規則的な傾向はありません。一般に、HGとh-BN間のvdW相互作用により、変形ポテンシャル定数が増加します。

有効質量は、キャリアと方向に依存するため、より複雑です。有効質量について注意すべき点が3つあります。まず、100％HGおよび100％-HG / h-BNヘテロ二重層の電子有効質量は等方性、つまり m *（ΓM）= m *（ΓK）。ヘテロ二層構造により、100％HG単層と比較して電子の有効質量がわずかに低下します。スタッキングパターンは、電子の有効質量にわずかな影響を及ぼします（4つのスタッキングパターンはすべて約0.90です）。次に、同じ水素化パターン（つまり、100％、25％のパターンI、および6.25％のパターンI）の下で、電子 m *（ΓK）は、水素被覆率の減少とともに減少します。水素被覆率がゼロに減少するため、限界は0.024（グラフェンの有効質量）であることが示されています。第三に、同じ水素被覆率の下で、有効質量も水素化パターンの影響を受けます。 25％HGの場合、パターンIの電子有効質量は他の2つよりもはるかに低くなります。つまり、有効質量は水素化の影響を受ける可能性が高くなりますが、弾性率や変形ポテンシャル定数の影響は受けません。

表2では、電子と正孔の移動度は上記のパラメータに基づいて計算されています。有効質量が影響を受けやすいため、移動度の傾向は有効質量の傾向と似ています。一般的に、水素化はグラフェンの移動度を劇的に低下させます。グラフェンの理論的移動度（3.2×10 ⁵ cm ² /（V s）[28]）は、HGよりも数桁高くなっています。さらに、HGには非対称（μ _e ≠μ _h ）および異方性（μ （ΓM）≠μ （ΓK））モビリティ。注意すべき3つの詳細があります。まず、同じ水素化パターンの下で、電子移動度は水素被覆率の増加とともに単調に減少します。しかし、異なる水素化パターンの下では、結論が常に確立されるとは限りません。たとえば、25％のパターンIIの移動度は、100％のHGの移動度よりも低くなります。次に、25％および6.25％のHGの場合、パターンIのμが高くなります。 _e 他のパターンと比較して。 μ _e （ΓK）25％パターンIは8985.85 cm ² /（V s）および6.25％のパターンIは23,470.98 cm ² /（V s）、黒フォスフォレン[24]およびMoS ₂ よりもはるかに高い [32]。第三に、h-BN基板は正孔移動度に大きく影響しますが、電子移動度にはほとんど影響しません。これは、積層パターンIおよびIIの正孔移動度がHG単分子層の正孔移動度に近いが、積層パターンIIIおよびIVの正孔移動度よりもはるかに低いことを示しています。したがって、異なるスタッキングパターンは、正孔の移動度に大きな影響を与えますが、電子の移動度にはほとんど影響を与えません。

さらに、100％HGの移動度は、すべての電子-フォノン相互作用、つまり経度音響（LA）、横音響（TA）、およびZAフォノンを考慮して再計算されました。結果は、電子移動度が105 cm ² であることを示しています。 /（V s）ΓK方向。図5は、電子-フォノン相互作用行列要素| g を示しています。 | LA、TA、ZAフォノンの。これは、LAフォノンが電子-フォノン相互作用で支配的であることを示しています。全体として、LAフォノンはTAおよびZAフォノンと比較して電子との相互作用強度が大きくなっています。移動度の値はDPA法で計算された値よりもわずかに低くなりますが、HGの2つの方法の違いは、アルセネン、アンチモネン、およびシリセンの場合よりもはるかに小さくなります。一般的に、DPA法は私たちの研究で実行可能です。

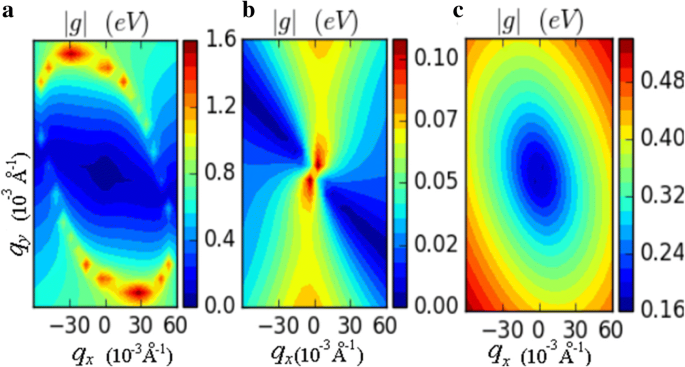
電子-フォノン相互作用行列要素| g | a の LA、 b TA、および c ZAフォノン

結論

要約すると、HG / h-BNヘテロ二重層のキャリア移動度は、この論文の第一原理計算に基づいて調査されました。移動度への影響は、HG / h-BNヘテロ二重層のスタッキングパターン、水素被覆率、および水素化パターンの観点から説明されています。弾性率 C _2D 、有効質量 m ^* 、および変形ポテンシャル定数 E ₁ 移動度を分析するために計算されます。変形ポテンシャル定数は、パターンが異なると規則的な傾向はありません。 HGの弾性率と有効質量は方向に依存します。結果は、ΓK方向の弾性率が高いことを示しています。有効質量は、さまざまな水素化とスタッキングパターンの影響を受ける可能性が高くなります。同じ水素化パターンの下で、電子移動度は水素被覆率の増加とともに単調に減少します。同じ水素被覆率の下で、異なるパターンは移動度の大幅な変化につながります。 25％および6.25％HGの場合、μ _e （ΓK）25％パターンIは8985.85 cm ² /（V s）およびμ _e （ΓK）6.25％のパターンIは23,470.98 cm ² /（V s）;どちらも他のパターンよりもはるかに高いです。 h-BN基板の影響については、積層パターンの違いが正孔移動度に大きく影響しますが、電子移動度にはほとんど影響しません。積層パターンIおよびIIの正孔移動度は、HG単分子層の正孔移動度に近いが、積層パターンIIIおよびIVの正孔移動度よりもはるかに低い。全体として、HG / h-BNヘテロ二層は、特定の水素化パターンの下でかなりのキャリア移動度とバンドギャップを持ち、エレクトロニクスとフォトニクスで有望なアプリケーションの見通しがあります。

略語

ATK：

Atomistix ToolKit

CBM：

伝導帯の最小値

DBG：

直接バンドギャップ

DFT：

密度汎関数理論

DPA：

変形ポテンシャル近似

FET：

電界効果トランジスタ

GGA：

一般化された勾配近似

h-BN：

六方晶窒化ホウ素

HG：

水素化グラフェン

IBG：

間接バンドギャップ

PBE：

Perdew-Burke-Ernzerhof

VBM：

価電子帯の最大値

vdW：

ファンデルワールス