SnxPy単分子層:高い安定性、キャリア移動度、および磁気特性を備えた新しいタイプの2次元材料
要約
強磁性、弾性異方性、キャリア移動度、調整可能なバンド構造を備えた2次元(2D)グループV材料を探すことは、絶えず開発されているナノデバイスを開発するための1つの鍵です。 2D単分子層Sn x P y x で / y (1 / 1、1 / 2、1 / 3など)配位数は、密度汎関数理論最適化と組み合わせた粒子群最適化手法に基づいて研究されます。その熱安定性は、70Kおよび300Kでの分子動力学によって確認でき、新しい2D材料が安定して存在することを示しています。 4つの安定した構造の電子バンド構造は、Sn x のすべての単分子層が P y 二軸ひずみ下で完全に調整可能で柔軟な調整可能なバンドギャップ半導体です。 P \(\ overline {4} {2} _1 \)m-SnP 2 の単分子層 独自の価電子帯構造を持つものは、「ストーナー基準」とPmc2 1 により、正孔ドーピングによって非磁性から強磁性に変化する可能性があります。 -SnP 2 は、面内弾性異方性を備えた直接型ギャップ半導体であり、800 cm 2 という高い電子移動度を備えています。 V -1 s -1 k に沿って b MoS 2 よりもはるかに高い方向 (〜200 cm 2 V -1 s -1 )。材料の吸光度のピークは紫外線領域にあります。これらの発見は、2D Sn x の新たな分野の潜在的なアプリケーションを拡大します P y ナノエレクトロニクスの構造。
はじめに
二次元(2D)二元化合物は、その独自の特性により近年大きな注目を集めており、ナノエレクトロニクスおよびオプトエレクトロニクスデバイスでの潜在的なアプリケーションに信頼できるガイダンスを提供できます[1]。たとえば、グラフェンはその発見以来、特性と潜在的な用途のために大きな関心を集めました[2,3,4,5,6]が、グラフェンは室温で検出できない小さなバンドギャップを持っているため、オプトエレクトロニクスナノデバイスでの使用が困難です。したがって、これらの困難により、研究者は理想的なバンドギャップを持つ2D材料を見つけることを決意するようになりました。次の年には、窒化ホウ素(BN)[7]、MoS 2 または他の遷移金属ジカルコゲニド[8,9,10,11,12,13]、および遷移金属トリカルコゲニド[14、15]などが出てきています。近年、IV族のグラフェンやその他の2D材料(シリコーン、スタネン、ゲルマネン[16])は、科学研究において大きな進歩を遂げています。ただし、グループVに属する2D半導体材料、特にフォスフォレン[17、18、19]とアルセネン[20]は、オプトエレクトロニクスデバイスの分野で新世代の候補として浮上しています。ホスフェンは、電界効果トランジスタ、オプトエレクトロニクスデバイス、スピントロニクス、ガスセンサー、ソーラーセルなどで幅広い用途が見込まれますが、2Dハニカム状構造のスタネンは、グラフェンに続く優れた物理的特性を備えた新しいタイプの材料と見なされています。その強い電子スピン軌道相互作用のため。
多機能で斬新な2D素材を得るには、2種類の要素を合成することが急務です。合金化は、2D材料の特性を改善してその適用性を拡大するためによく使用されると報告されています。たとえば、2D MoS 2x Se 2(1 − x ) およびWS 2x Se 2(1 − x ) ナノシート[21、22]は、調整可能な電子的、光学的特性、および x による面内の負のポアソン比などの奇妙な特性を示しています。 / y (1 / 1、1 / 2、1 / 3など)配位数。別の例として、2D合金材料Si x C y [23]、B x C y [24]、およびB x Si y [25]は、第一原理計算により、純粋な基底状態とは異なる多くの新しい特性(新しい構造、電子的、および機械的特性)を示しています。 2Dフォスフォレンとスタネンの単分子層は新しい特性を持っているため、SnとPの元素はさまざまな化学量論と化合物でした。
この作業では、粒子群最適化(PSO)アルゴリズムによっていくつかの構造を構築しました。次に、2D Sn x の最も安定した4つの構造を選び出しました。 P y 異なる配位数を持つ単分子層であり、密度汎関数理論(DFT)最適化に基づいて電子特性を調査しました。計算された電子バンド構造は、異なる配位数を持つすべての安定または準安定単分子層が間接バンドギャップを持つ半導体であることを示唆しています。さらに重要なのは、Pmc2 1 -SnP 2 単分子層は、赤外光領域で0.92eVの有限バンドギャップを持つ直接的なギャップ半導体です。しかしそれを超えて、Pmc2 1 -SnP 2 構造は直接のようなギャップ半導体であり、約800 cm 2 の高い電子移動度を備えています。 V -1 s -1 、MoS 2 よりもはるかに高い (〜200 cm 2 V -1 s -1 )。 P \(\ overline {4} {2} _1 \)m-SnP 2 の単分子層 独自の価電子帯構造を持つ構造は、「ストーナー基準」により、正孔ドーピングによって非磁性から強磁性に変化する可能性があります。計算された電子バンド構造は、Sn x のすべての単分子層を示唆しています。 P y は、二軸ひずみ下で柔軟に調整可能なバンドギャップを備えた半導体であり、可視光範囲のほぼ全体で4つの構造のバンドギャップのひずみ工学を可能にします。
計算方法
構造の多様性の徹底的な調査を保証するために、さまざまな x および y 粒子群最適化(PSO)アルゴリズム[26]に基づいて、1から6までの選択が考慮されます。単分子層構造が得られた検索結果は、 y についてのみ比較的安定しています。 / x ≧1。
2D Sn x の電子構造を研究するには P y 配位数の異なる単分子層については、平面波密度汎関数理論(DFT)[27、28]法を使用して計算を行い、Vienna Ab-initio Simulation Package(VASP)[29,30,31]で実現しました。一般化勾配近似(GGA)を使用して、交換相関エネルギーをPer-dew–Burke–Ernzerhof(PBE)[32,33,34,35]の形式で記述し、電子イオンポテンシャルを射影増幅で記述します。波法[33]。平面波のカットオフエネルギーは、Sn x に対して500eVのエネルギーになるように選択されました。 P y それぞれシステム。逆格子空間の十分に密なk点(9×9×1)がブリルアンゾーンでサンプリングされました。隣接するスーパーセル間の平面に垂直な真空空間は25Åより大きく、複製間の相互作用を排除します。 2つの連続したステップの計算では、10 5 として設定されます。 エネルギー収束値としてのeV。幾何学的最適化中、すべての構造の原子力は0.02eVÅ -1 未満です。 原子が最適な位置に到達するまで共役勾配法を使用します。さらに、Noséアルゴリズム[36]が300Kの場合、ab initio分子動力学(AIMD)計算に4×4×1のスーパーセルを使用します。
キャリア移動度は、主に音響側波散乱、光側波散乱、およびイオン化不純物散乱の影響を受けます。後者の2つは最初の2つほど影響力がないため、計算した移動度には音響側波散乱下の移動度が含まれます。移動度は主にトランジスタの2つの性能に影響を与えます。1つは、キャリア濃度が一緒になって半導体材料の導電率(抵抗率の逆数)を決定することです。第二に、それはデバイスの動作周波数に影響を与えます。バイポーラトランジスタの周波数応答特性の主な制限は、少数キャリアがベース領域を通過する時間です。移動度は、2D半導体材料の導電率を測定するための重要なパラメータです。半導体材料の導電率を決定し、デバイスの動作速度に影響を与えます。したがって、キャリア移動度はフォノン分散によって制御され、BardeenとShockleyによって提案された変形ポテンシャル(DP)理論によって説明できます[37]。したがって、2D材料のキャリア移動度は[38、39]
として表すことができます。 $$ {\ mu} _ {2D} =\ frac {2e {\ mathrm {\ hslash}} ^ 3 {C} ^ {2D}} {3 {k} _BT {\ left | {m} ^ {\ ast } \ right |} ^ 2 {E} _1 ^ 2} $$ここで e 、ℏ、および k B は、それぞれ電子電荷が減少したプランク定数とボルツマン定数です。そして T 300Kに設定した温度です。ここで m * は有効質量、 E 1 は変形ポテンシャル定数であり、 C 2D は面内剛性です。
小波数ベクトルの下でのライトフィールドに対するシステムの線形効果は、複素誘電率の虚数部と、によって計算できる誘電関数によって決定されます。
$$ \ upvarepsilon \ left(\ omega \ right)={\ varepsilon} _1 \ left(\ omega \ right)+ i {\ varepsilon} _2 \ left(\ omega \ right)$$ここで、ε 1 (ω )およびε 2 (ω )は関数の実数部と虚数部εです。 1 (ω )虚数部εから導出できます 2 (ω )クラマース・クローニッヒによる誘電関数は表現できます[40]。誘電関数の虚数部は次のように表すことができます
$$ {\ varepsilon} _2 \ left(\ omega \ right)=\ frac {4 {\ pi} ^ 2} {m ^ 2-{\ omega} ^ 2} \ sum \ Limits_ {V、C} \ underset {BZ} {\ int} {d} ^ 3k \ frac {2} {2 \ pi} {\ left | e \ bullet {M} _ {cv} \ right |} ^ 2 \ times \ updelta \ left [{ E} _C \ right。(k)-{E} _V(k)-\ mathrm {\ hslash} \ left。\ omega \ right] $$また、吸収係数 I (ω )は
によって取得されました $$ I \ left(\ omega \ right)=\ sqrt {2} \ omega \ left [\ sqrt {\ varepsilon_1 ^ 2 \ left(\ omega \ right)-{\ varepsilon} _2 ^ 2 \ left(\ omega \ right)}-{\ varepsilon} _1 \ left(\ omega \ right)\ right] 1/2 $$ここで、 C は伝導帯、 V は価電子帯の状態、Ω はユニットセルの体積、 m は自由電子の質量、 e は自由電子の電荷であり、ω は入射光子の周波数です。
結果と考察
安定性
まず、4つの2D Sn x P y 単分子層は、それらのエネルギー安定性を決定するために考慮されました。地層エネルギーは、熱力学系のエネルギーパラメータであり、システムの安定性をチェックするための重要なポイントです。 Sn x の相対的な安定性 P y 単分子層は、形成エネルギーを計算することで確認でき、次のように計算されます
$$ {E} _ {\ mathrm {form}} =\ left({E} _ {\ mathrm {total}}-{N} _ {\ mathrm {Sn}} {E} _ {\ mathrm {Sn} }-{N} _ {\ mathrm {P}} {E} _P \ right)/ \ left({N} _ {\ mathrm {Sn}} + {N} _ {\ mathrm {p}} \ right) $$ここで E は、特定の圧力での化合物または構成要素のエネルギーです。 N はユニットセル内の原子の数です。計算されたシステムの負の形成エネルギーは、構成が安定または準安定であることを示します[41]。 Sn x の計算された形成エネルギー P y 単分子層は、それぞれ− 0.235、− 0.223、− 0.159、および− 0.016 eV /原子です(表1に示されています)。その定義によれば、値が小さいほど安定性が高いことを示します。明らかに、P \(\ overline {6} \)m2-SnPはこれら4つの構造の中で最も安定しています。より具体的には、半導体材料の高い熱安定性は、電子デバイスの用途において特に重要である。ここで、Sn x の熱安定性 P y 非経験的分子動力学(AIMD)シミュレーションを使用して調べた単分子層。空間群の対称性に基づいて、同様の構造P \(\ overline {6} \)m2-SnPおよびPmc2 1のP \(\ overline {6} \)m2-SnPの安定性を計算します。 -SnP 2 およびPmc2 1 -SnP 2 Pmc2 1 の場合 -SnP 2 およびP \(\ overline {4} {2} _1 \)m-SnP 2 構造。結果は、構造の総エネルギーの平均値がほとんど変化せず、1 ps、3 ps、および5 ps後も構造が変化しないことを示しており、Sn x P y 単分子層は熱的に安定しています(図S1)。次に、フォノン分散曲線を計算しましたが、仮想の振動周波数がないということは、構造が動的に安定していることを意味します(図S1)。マイクロメカニカル劈開[2]、エピタキシャル成長[42]、化学蒸着[43]、液体剥離[44]など、層状材料を合成するためのいくつかの方法が文献で報告されています。同様の構造を持ついくつかの材料は、実験的にうまく調製されました。実験では、いくつかの層のGaSeナノシートが高性能光検出器になっているという関連する報告がいくつか見つかりました[45]。さらに、MoS 2 の大きなサイズの超薄層の準備、分離、および迅速で明確な特性評価 、GaS、およびGaSeがSiO 2 に堆積 / Si基板が報告されています[46]。
<図>図1a、bにプロットされているように、P \(\ overline {3} \)m1-SnPの構造は、P \(\ overline {6} \)m2-SnP円筒相と同様の構造を示します。 Pmc2 1 -Sn P 2 三角相(図1c)は、 x / y 組成はさらに1/2に増加します。 P \(\ overline {4} \)2 1 に類似した構造の材料 m-SnP 2 理論計算によって安定していることが証明されました[47]。また、新しい研究では、XY 2 の構造が見つかりました (図1d)は間接バンドギャップ半導体であり、電界や応力の影響を受けやすい可能性があります。私たちが予測する資料は、将来、技術の開発によって準備が成功すると信じています。
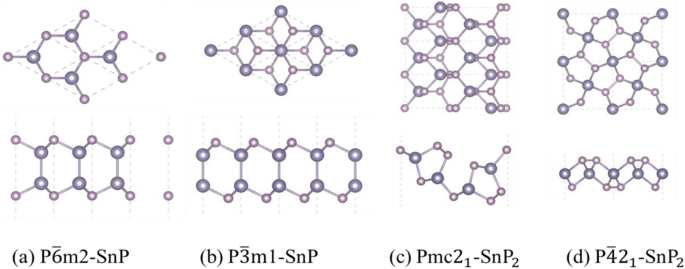
Sn x の原子構造の上面図と側面図 P y 単層: a P \(\ overline {6} \)m2-SnP、 b P \(\ overline {3} \)m1-SnP、 c Pmc2 1 -SnP 2 、および d P \(\ overline {4} {2} _1 \)m-SnP 2 ;フェルミ準位(水平の破線)は0eVにシフトします。濃いピンクの球はSn原子を表し、薄いピンクの球はP原子を表します
電子的および磁気的特性
計算されたバンド構造とSn x の部分状態密度 P y 単分子層を図2にプロットします。図2aに示すように、P6̅m2-SnPはバンドギャップ1.19eVの間接半導体です。 Γ→K方向の価電子帯最大値(VBM)は、混成Sn-p軌道とP-p軌道によってもたらされますが、K点での伝導帯最小値(CBM)は、混成Sn-s軌道とP-p軌道に由来します。 P \(\ overline {3} \)m1-SnPは、P \(\ overline {6} \)m2-SnPの対応物と同様の電子バンド構造を示しますが、バンドギャップは1.21eVと小さくなっています。 Γ点とフェルミ準位( E )付近のP \(\ overline {6} \)m2-SnPとP \(\ overline {3} \)m1-SnPの価電子帯分散 F )は、状態密度(DOS)がかなり高く、VBMの周りにファンホーベ特異点があることを考えると、非常にフラットです。 Pmc2 1 -SnP 2 直接のようなギャップ半導体特性を示します( E g (直接)− E g (間接)=6 meV)、バンドギャップは0.72 eVです(図2cを参照)。そのVBMは主にP-p軌道に起因しますが、そのCBMは主にP-p軌道とSn-s軌道に起因します。 P \(\ overline {4} {2} _1 \)m -SnP 2 E を備えた間接ギャップ半導体です。 g 1.79 eVであり、に由来するバンドは図2cに類似しています。さらに重要なのは、P \(\ overline {4} {2} _1 \)m-SnP 2 単分子層は図2a、bと比較して同様の状態であり、VBMの周囲にフラットバンド分散特性も生じ、非常に高いDOSとファンホーベ特異点をもたらします。
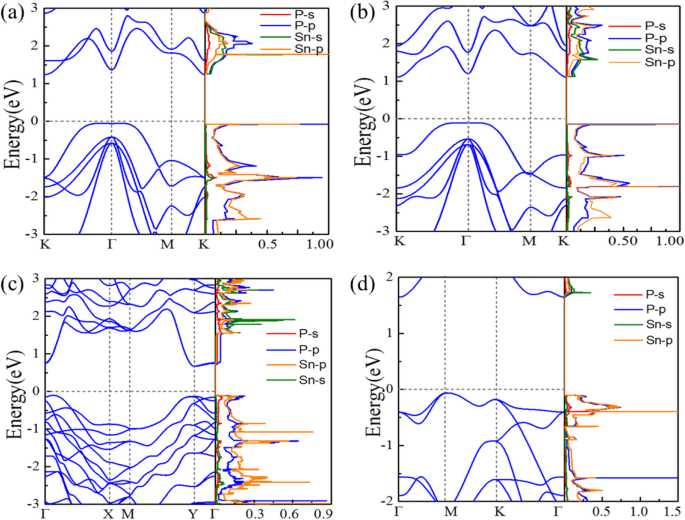
計算された電子バンド構造とSn x のVBMおよびCBMの部分状態密度 P y 単層: a P \(\ overline {6} \)m2-SnP、 b P \(\ overline {3} \)m1-SnP、 c Pmc2 1 -SnP 2 、および d P \(\ overline {4} {2} _1 \)m-SnP 2
ストーナーの基準によると、運動エネルギーが交換分裂エネルギーよりも小さい場合、つまり E のDOSが小さい場合、自発的な強磁性が発生します。 F 十分に高いです。図2dは、VBM周辺の非常に高いDOSを示しています。 P \(\ overline {4} {2} _1 \)m-SnP 2 E の場合、ストーナー基準を満たす可能性があります F 正孔ドーピングによりDOSが高い位置にシフトします。図3aに示すように、正孔ドーピングは適切なドーピング濃度で磁気モーメントを導入することができます。予想どおり、計算結果は、P \(\ overline {4} {2} _ 1 \)m-SnP 2 臨界正孔密度を超えて強磁性基底状態に変換される可能性があります。その中で、穴の密度 n h n として表すことができます h = m h / S セル 、ここで S セル および m h プリミティブセルの面積とプリミティブセルに導入された穴の数です。単分子層への穴の注入P \(\ overline {4} {2} _1 \)m-SnP 2 確かに強磁性につながります。磁気モーメントは、正孔密度と急なピークのような関係を示します。かなりのスピンモーメントがシステム内の正孔ドーピングによって引き起こされるため、フェルミ準位周辺のエネルギーバンド構造はスピン分裂によって大きく変化しました。特に、P \(\ overline {4} {2} _1 \)m-SnP 2 のスピン偏極バンド構造(図3bに示す) 7.2×10 14 cm −2 単分子層が完全なハーフメタルになることを示しています。したがって、P \(\ overline {4} {2} _ 1 \)m-SnP 2 で、金属量が半分の安定したFM状態を実現できると予測します。 単層。
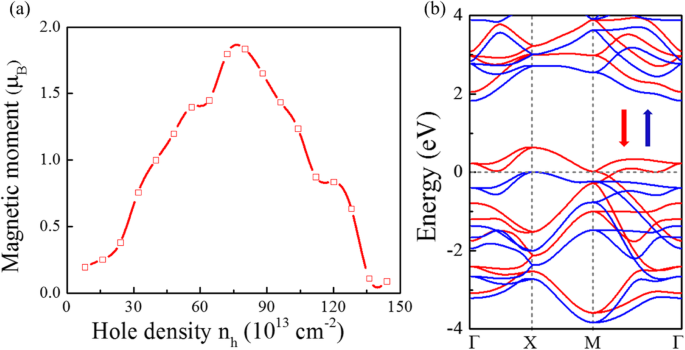
P \(\ overline {4} {2} _1 \)m-SnP 2 の強磁性 単層。 ( a )スピンモーメントと穴密度 n h 。 b P \(\ overline {4} {2} _1 \)m-SnP 2 の計算された価電子帯構造 n で h =7.2×10 14 cm −2 。スピンアップバンドとスピンダウンバンドは、それぞれ青と赤で表示されます。フェルミ準位は0eVに設定されています
単分子層の弾性異方性とキャリア移動度
2D単分子層Sn x の電子特性に対するひずみの影響 P y 構造も面白いです。図4aは、二軸ひずみεの下でのエネルギーギャップの変化を示しています。 。 Sn x のエネルギーギャップ P y 単分子層は、いくつかの規則に従って著しく変調されます。たとえば、P \(\ overline {6} \)m2-SnPのエネルギーギャップは、引張ひずみがεまで増加すると、1.19から0.52eVに減少します。 =8%、最初にεの1.12から1.36eVに増加 2%、その後1.36から0.51eVに減少します。また、 a および b Pmc2 1 の格子定数の -SnP 2 構造が異なり、電子特性の変化が x に沿って異なります -軸と y -軸[48]、図4bに示すように。一軸ひずみが異なる方向に加えられると、 x が変化することは明らかです。 方向は y の変化とは異なります 方向。ひずみεによるエネルギーギャップの範囲を考慮する 、面内ひずみによる調整可能なバンドギャップの範囲は、第一原理計算に基づいて、可視光領域全体をほぼカバーしています。
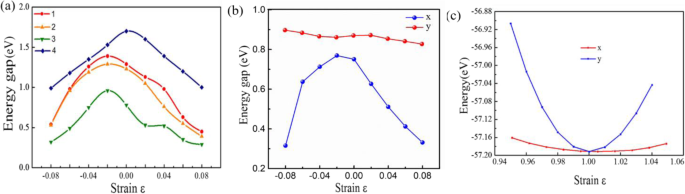
構造のひずみ依存電子特性:(1)P \(\ overline {6} \)m2-SnP、(2)P \(\ overline {3} \)m1-SnP、(3)Pmc2 1 -SnP 2 、および(4)P \(\ overline {4} {2} _1 \)m-SnP 2 。 b Pmc2 1 の一軸ひずみ依存電子特性 -SnP 2 。 c Pmc2 1 のエネルギー -SnP 2 単層対一軸染色
また、図4cに示すように、一軸応力の影響も調べました。面内剛性 C 2D ( C 2D =[∂ 2 E /∂δ 2 ] / S 0 、ここで S 0 2D Pmc2 1 の面積です -SnP 2 単層)は放物線をフィッティングすることで得られます。興味深いことに、面内剛性 C 2D a に沿って非常に明白な弾性異方性を示します および b 方向はそれぞれ12.1と105.6N / mと計算されます。 Pmc2 1 -SnP 2 直接のようなギャップ半導体特性、有効質量( m ∗ =ℏ 2 (∂ 2 E / ∂K 2 ) -1 )電子( m e は| m * e |)と穴( m h は| m * h |)(準)直接半導体Pmc2 1 に関連付けられています -SnP 2 単分子層も計算されます。有効質量を示します(表2)。最も興味深いのは、 k の電子の有効質量です。 b 方向(0.15 me)は k の方向よりもはるかに小さい a 方向(1.31 me)、 k での電子の容易なドリフトを示します b 方向。もう1つの重要なパラメータは、DP定数 E です。 1 ( E 1 =d E エッジ / d δ ) a に沿った電子の場合 および b 方向はそれぞれ5.36と11.57eVと計算されます。驚いたことに、計算されたキャリアは約800 cm 2 を達成することができます V -1 s -1 k で b 方向。比較として、MoS 2 のキャリア移動度 単層は〜200 cm 2 V -1 s -1 実験で[8]。ただし、キャリアの移動度は約8 cm 2 です。 V -1 s -1 k で a 方向。したがって、この研究で見つかった高いキャリア移動度は、電子輸送の研究にとって非常に重要です。
<図>光学特性
光電子材料の光電特性は、誘電関数、光伝導性、および吸収係数によって特徴付けられます。誘電関数の虚数部を図5aに示します。 Pmc2 1 に注意してください -SnP 2 単分子層は〜0.70 eVで始まる吸収を示し、〜0.9、〜3.2、および〜4.0eVで3つの主要な吸収ピークが現れます。図5bに示すように、単分子層Pmc2 1 の可視範囲と紫外線範囲の3方向すべての吸光度を示しています。 -SnP 2 。したがって、Pmc2 1 -SnP 2 単層材料は、たとえば炎の効率的な検出のために、原子的に薄いソーラーブラインド光検出器に使用できます。
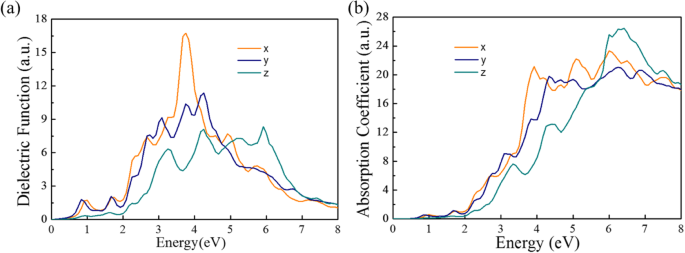
a Pmc2 1 の計算された誘電関数とエネルギーの関係 -SnP 2 さまざまな入射光の方向に沿って。 b 計算された虚数吸収係数
結論
結論として、第一原理計算と組み合わせたPSOアルゴリズムに基づいて、いくつかの2D Sn x を特定しました。 P y x の比率の単分子層 / y =1:1および1:2。驚くべきことに、これらの新しい単分子層は、独特の電子的および磁気的特性も備えています。P\(\ overline {4} {2} _1 \)m-SnP 2 の単分子層です。 独自の価電子帯構造を持つ構造は、「ストーナー基準」により、正孔ドーピングによって非磁性から強磁性に変化する可能性があります。 Pmc2 1 -SnP 2 構造は、面内弾性異方性を備えた直接のようなギャップ半導体であり、800 cm 2 という高い電子移動度を持っていることがわかります。 V -1 s -1 k に沿って b MoS 2 よりもはるかに高い方向 (〜200 cm 2 V -1 s -1 )。材料の吸光度のピークは紫外線領域にあります。これらの発見は、2D Sn x の新たな分野の潜在的なアプリケーションを拡大します P y ナノエレクトロニクスの構造。多機能Sn x のこれらの望ましい特性 P y 単分子層は、エレクトロニクスおよびオプトエレクトロニクスにおける有望な優れたアプリケーションを提供します。
データと資料の可用性
それらはすべて本文と図にあります。
ナノマテリアル
- 超伝導体とは:タイプ、材料、特性
- 材料:表面特性が改善され、充填挙動が最適化されたEPPフォーム
- Python の type() と isinstance() と例
- コバルトをドープしたFeMn2O4スピネルナノ粒子の調製と磁気特性
- リチウムイオン電池用のCr3 +およびF-複合ドーピングを用いたLiNi0.5Mn1.5O4カソード材料の合成と電気化学的性質
- MnХFe3−XО4スピネルの構造的および磁気的特性に及ぼす接触非平衡プラズマの影響
- ナノカーボンフィラーの電界支援配向による複合材料の電気的性質
- ポリ(4-スチレンスルホン酸-co-マレイン酸)による金磁性ナノ粒子の安定性の向上:タンパク質検出用に調整された光学特性
- RGOと3次元グラフェンネットワークが高性能でTIMを共同修正
- 高度に圧縮耐性のあるスーパーキャパシタ電極としての超弾性と高静電容量を備えたグラフェン/ポリアニリンエアロゲル
- Ag n V(n =1–12)クラスターの構造的、電子的、および磁気的特性の調査



