ナノスケールひずみ場によるAlNの屈折率に及ぼす転位の影響

はじめに

AlNベースの材料は、発光ダイオード（LED）[1,2,3,4,5]、レーザーダイオード[6,7,8]、光検出器[1,2,3,4,5]などの深紫外線（DUV）オプトエレクトロニクスデバイスを製造するための有望な材料です。 9、10] 3.4から6.2eVに調整可能な直接バンドギャップによる[11]。 AlNの屈折率は、オプトエレクトロニクスデバイスの性能に直接影響します。 LEDの場合、全反射角はAlN層と他の領域との屈折率の差によって決定されるため、AlNの屈折率は光抽出効率（LEE）に影響を与えます。これは、量の重要な制限要因です。光出力の。外部量子効率（EQE）は内部量子効率とLEEの積であるため、AlNの屈折率はLEDのEQEに影響を与えます。また、屈折率は、分布ブラッグ反射鏡（DBR）[12,13,14]などの導波路構造の設計において重要な役割を果たします。DBRの反射率は屈折率に敏感です。したがって、AlNの屈折率に影響を与える要因を明らかにすることが重要です。これまでの研究から、AlNの屈折率は、温度、圧力、バンドギャップなどの多くの要因の影響を受ける可能性があることがわかります。 AlNの屈折率は、温度が高くなると[15]、圧力が低くなると[16]増加します。 AlNベースの材料の場合、バンドギャップが大きくなると屈折率は低くなります[17]。また、半導体の転位は、半導体の特性やデバイスの性能に大きな影響を与えます。転位は材料の応力を解放します[18]。それらはまた、光検出器の暗電流と応答性に影響を与え[19]、複数の量子井戸のIQEに影響を与えます[11、20]など。ただし、AlN材料には通常10 ⁸ の高いTDDがありますが、AlNの屈折率に対するさまざまな貫通転位密度（TDD）の影響に焦点を当てた研究はほとんどありません。 〜10 ⁹ cm ^{− 2} 最近のレポートからの注文[21、22、23]。 TDDとAlNの屈折率の相関関係を調査することは、オプトエレクトロニクスデバイスの性能を最適化するための鍵です。この論文では、AlNの屈折率に対するさまざまなTDDの依存性を研究しました。 633 nm、365 nm、280nmなどのさまざまな光子波長が使用されます。結果は、転位がAlNの屈折率の低下につながることを示しています。結果は、DUVLEDやDBR構造などのAlNベースのオプトエレクトロニクスデバイスの設計とシミュレーションに役立ちます。

メソッド

転位とAlNの屈折率の関係を研究するために、AlNテンプレートをc-サファイア基板上に有機金属化学気相成長法（MOCVD）で成長させ、さまざまな温度でアニールして、さまざまな転位密度のAlNサンプルを取得しました。

MOCVDでAlNテンプレートを成長させる場合、前駆体ガスとしてトリメチルアルミニウムとアンモニアを使用しました。キャリアガスとして水素を使用した。成長中の圧力は40mbarに保たれました。核形成層の成長温度と時間は、150°Cで約955°Cであり、その後、高温（HT）AlN成長のために1280°Cに上昇します。 15分間の高温AlN成長後、AlN中間層を1050°Cで160秒間成長させました。最後に、成長温度を1280°Cに上げて、厚いHTAlNを50分間成長させました。 AlN膜の総厚は約1.1μmです。

MOCVDによるAlN層の成長後、AlNテンプレートをそれぞれ1500°C、1600°C、1700°C、および1750°Cで1時間exsituアニーリングしました。アニーリングなしのAlN層をサンプル1としてマークし、1500°C〜1750°Cのアニーリング後のサンプルをサンプル2〜5としてマークしました。X線回折（XRD）を使用して、AlNサンプルのTDDを測定しました。分光エリプソメトリー（SE）測定は、屈折率を測定するために行われました。ラマンシフトスペクトルを採用して、AlNテンプレートの応力状態を特徴付けました。

結果と考察

図1aおよびbは、5つのAlNサンプルの（0002）および（10-12）平面XRDロッキングカーブ（XRC）を示しています。 （0002）平面XRCの半値全幅（FWHM）がわずかに減少し、（10–12）平面XRCのFWHMがサンプル1からサンプル5にかけて大幅に減少していることがわかります。成分は、式（1）および（2）に従って（0002）および（10–12）平面XRCのFWHMを使用して計算できます：[24、25]。

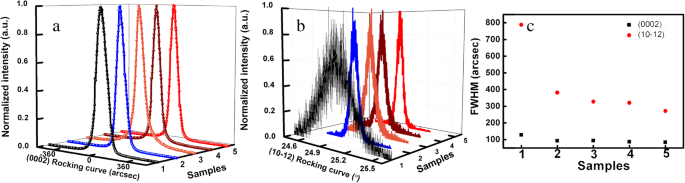
a 5つのAlNサンプルの（0002）平面XRC。 b 5つのAlNサンプルの（10-12）平面XRC。 c （0002、10-12）平面XRCのFWHM;赤い丸は（10-12）面のFWHMを意味し、黒い四角は（0002）面のFWHMを表します

ここで、ρ _s およびρ _e それぞれスクリューとエッジ成分による転位の密度を表します。 β XRCのFWHMです。 | b _c | c軸格子定数に相当し、| b _a | AlNのa軸格子定数に相当します。 （0002）および（10–12）平面XRCのFWHMを5つのAlNサンプルについて図1cに示し、5つのAlNサンプルの計算されたTDDを表1に示します。

5つのサンプルのSE実験データは、ダイレクトバンドギャップ半導体の光学特性を効果的に再現できるパラメトリック半導体モデルを使用して、CompleteEASEソフトウェア（J.A. Woollam Inc.）によって適合されます[26]。図2aは、5つのサンプルの部分的な実験曲線とフィッティング曲線を示しています。 5つのサンプルの平均二乗誤差（MSE）は、それぞれ8.139、8.536、9.175、10.560、および9.821であり、良好なフィッティング結果が確認されます。すべてのデータとフィッティング結果は、追加ファイル1で提供されます。

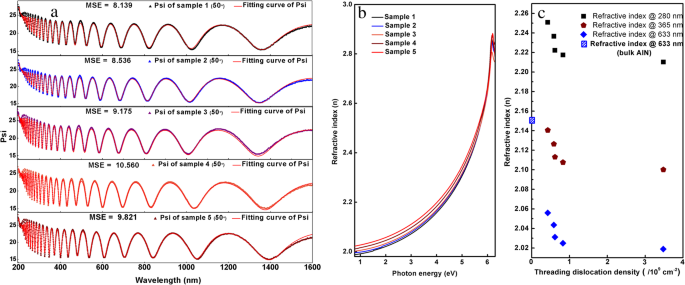
a SE測定とフィッティング曲線の部分的な実験データ。 b 屈折率曲線。 c 屈折率と280nm、365 nm、および633nmでのさまざまなTDDの比較

5つのサンプルの屈折率曲線は、図2bに示すフィッティング結果から取得できます。光子エネルギーがAlNのバンドギャップ（約6.2 eV）よりも低い場合、5つのサンプルすべての光子エネルギーの増加に伴って屈折率が増加します。ただし、光子エネルギーが6.2 eVを超えると、光子エネルギーの増加に伴って屈折率が低下します。この現象は、クラマース・クローニッヒ分散関係によって説明できます。 AlNのTDDが減少すると、屈折率は633 nmで2.019から2.056に増加し、バルクAlNの屈折率（633 nmで2.15 [27]）に近くなります。これは、AlNの転位により、バルクAlN結晶の屈折率よりも屈折率が小さくなることを意味します。

4.42 eV（280 nm、ソーラーブラインドUV）、3.40 eV（365 nm、GaNのバンドギャップ）、1.96 eV（633 nm）での屈折率とTDDの関係を、図2cと表1に示します。 .TDDの増加に伴い、AlNの屈折率が低下することがわかります。転位密度が4.24×10 ⁸ から増加すると 〜3.48×10 ⁹ cm ^{− 2} 、AlNの屈折率は280nmで2.2508から2.2102に減少します。

転位がAlNの屈折率をどのように変化させるかについてのメカニズムを明らかにするために、転位によって誘発されるひずみ場を研究します。屈折率と発生するひずみの関係は、式（3）[28]：

式では、 p _ij 弾性光学テンソルと S ひずみの存在です。光弾性定数行列 P ウルツ鉱型AlNの式は式（4）[29、30]として示されています。

AlNにおけるらせん転位と刃状転位のひずみ場行列を考察する。 2種類の転位の円筒リングモデルを図3に示します。モデルによれば、単一転位の周りのひずみ場の分布を得ることができます[31、32]。

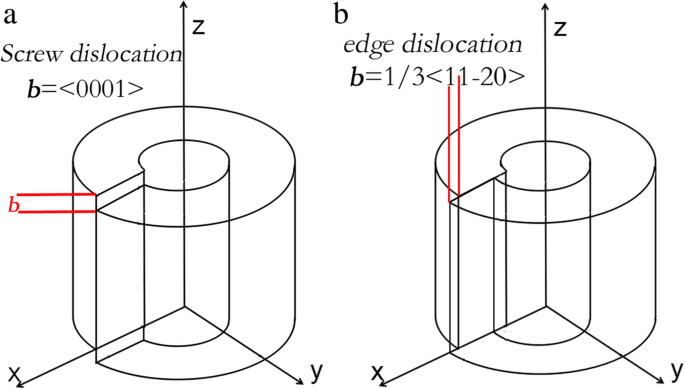
a の円筒リングモデル らせん転位と b エッジ転位

ユニットスクリュー転位の周りのひずみ場は次のように書くことができます：

単位刃状転位の周りのひずみ場は次のように書くことができます：

ここで b は、単位転位と e のバーガースベクトルの長さです。 転位の周りのひずみを表します。 G =121GPaはウルツ鉱型AlNのせん断弾性率です。 λ =117.1GPaおよび v =0.241は、それぞれラメ定数とポアソン比[33、34]です。 e 間の対応によると _ij および S _k （ i 、 j = x 、 y 、 z ; k =1,2,3 ... 6）[35]、転位によって引き起こされる屈折率の変化をさらに示すために、以下のようにひずみ場をマトリックス形成に変換します。

行列（7）と（8）を式（3）に入れると、Δ n の式を得ることができます。 ユニットのネジとユニットのエッジのずれが原因です。

計算に基づいて、ユニットスクリューとユニットエッジ転位の周りの屈折率（例として633 nmの屈折率）の分布を図4に示します。これは、転位の周りの屈折率が半径方向に沿って変化することを示しています。不均一な媒体と見なすことができる転位コアから。したがって、AlNを伝搬する光は、それに対応してTDDの影響を受けます。光が転位の周りのこれらの屈折場を通過するとき、散乱と干渉が起こります[36]。その結果、AlNの屈折率が変化します。これは、不均一な媒体の散乱行列に対応しています[37]。

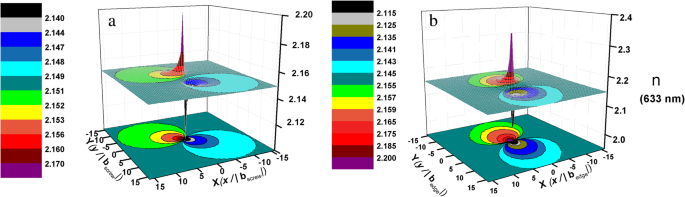
a 周辺の633nmでの屈折率の分布 ユニットスクリュー転位と b ユニットエッジ転位

「はじめに」のセクションで述べたように、屈折率が転位によって本当に影響を受けることを証明するために、他の影響要因を取り除く必要があります。温度の影響を避けるために、すべてのサンプルは室温で測定されました。 AlN材料の応力の影響を取り除くために、ラマンスペクトルを使用してAlNの応力を確認し、その結果を図5に示します。 E _g 750 cm ^{− 1} でのサファイアのモードピーク キャリブレーションとして使用されます。 AlN E のラマンシフトピーク ₂ （ h ）表1に示すように、TDDの減少に伴って青方偏移します。 E の青方偏移 ₂ （ h ）ピークは、AlNがサファイア基板からますます圧縮応力を受けることを意味します。ただし、圧縮応力の増加に伴い、屈折率は633nmでバルクAlNの屈折率に近くなります。 AlNの応力が不均一な基板に悩まされていることは、屈折率にほとんど影響を与えないことがはっきりとわかります。結論を裏付ける追加の証拠は、AlNがSi基板から引張応力を受ける場合、AlNの屈折率もバルクAlNの屈折率よりも小さいことです[38]。これは、この作業でAlNが圧縮応力を受ける条件と同じです。この現象は、AlNの応力が基板にかかるのが小さすぎて、AlNの屈折率を大きく変えることができないという事実に起因する可能性があります。その結果、他の要因の影響と比較して、AlNの屈折率に対する基板からの応力の影響を無視することができます。

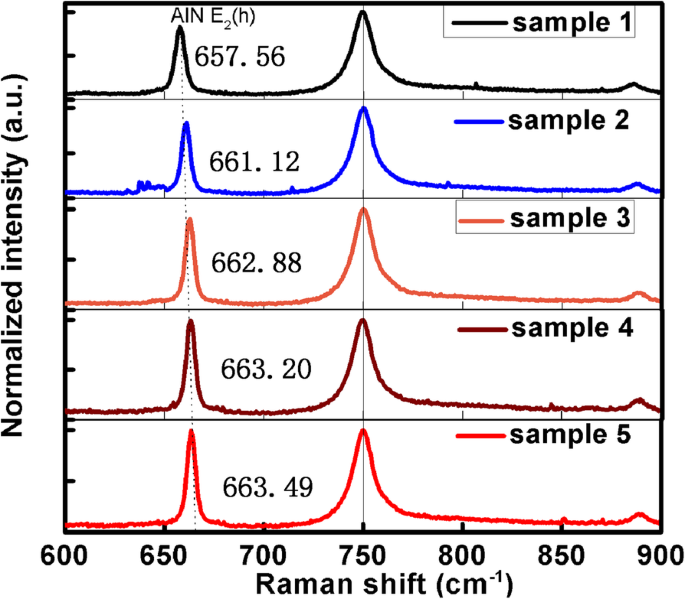
5つのサンプルのラマンシフトスペクトル

5つのサンプルのバンドギャップもここで計算されます。吸光係数α SEフィッティング結果から抽出され、バンドギャップ E _g 以下の式に基づいて計算されます[39]：

（αEのプロット ） ² 対 E 図6として示されています。 x の切片 -axisは E の値です _g 。 x のフィッティングカーブの切片から -軸、サンプル1からサンプル5の6.1106から6.1536eVへのバンドギャップの増加を図6に示します。屈折率とバンドギャップの関係を以下に示します[16]。

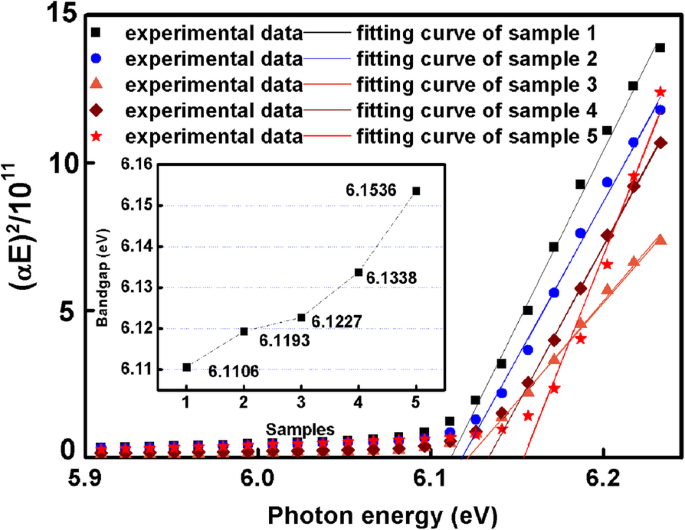
（αEの依存性 ） ² オン（ E ）、挿入図はAlNテンプレートのバンドギャップを示しています

ここで E は光子エネルギーであり、 E _g AlNのバンドギャップです。 a および b AlNの場合はそれぞれ13.70と7.81に等しい定数です。 E の増加に伴い、AlNの屈折率は低下するはずです。 _g 式によると。ただし、この作業では、 E の増加に伴ってAlNの屈折率が増加します。 _g これは、TDDの影響と比較して、AlNの屈折率に対するバンドギャップの影響を無視できることを意味します。したがって、TDDの変化は、AlNの屈折率の変化に重要な役割を果たします。

上記の分析と組み合わせると、ナノスケールのひずみ場が転位周辺の屈折率の分布に影響を及ぼし、AlNの屈折率にさらに影響を与えることが確認されています。実験データによると、転位はAlNの屈折を減少させます。

結論

結論として、AlNの屈折率に対するTDDの影響は、実験的および理論的に研究されています。温度、応力、バンドギャップの影響を排除すると、TDDの増加に伴ってAlNの屈折率が低下するという結論を得ることができます。さらなる研究は、転位の周りのナノスケールのひずみ場が、転位の周りで屈折率を著しく変化させる結果となることを示した。光が転位を伝播すると散乱と干渉が発生し、AlNの屈折率が変化します。この研究の結果は、AlNベースのDUVオプトエレクトロニクスデバイスを最適化するのに役立ちます。

データと資料の可用性

すべてのデータは、適切なリクエストに応じて提供できます。

略語

DBR：

分布ブラッグ反射鏡

DUV：

深紫外線

EQE：

外部量子効率

FWHM：

半値全幅

LED：

発光ダイオード

LEE：

光抽出効率

MOCVD：

有機金属化学蒸着

MSE：

平均二乗誤差

SE：

分光エリプソメトリー

TDD：

貫通転位密度

XRC：

XRDロッキングカーブ

XRD：

X線回折