密集した円偏光異常渦ビームの特性とトラップされたナノ粒子に対するその光学力
要約
高開口数(NA)の対物レンズで集束された円偏光異常渦ビーム(CPAVB)の特性を解析的および理論的に研究します。これは、トポロジカル電荷がビームプロファイルに大きな影響を与える可能性があり、NAとトポロジカル電荷を変調することでフラットトップ(FT)ビームを取得できることを示しています。スピンから軌道への角運動量の変換が、厳密に焦点を合わせた後、縦方向の成分で発生する可能性があることを発見するのは興味深いことです。さらに、ナノ粒子にしっかりと集束されたCPAVBの光学力が詳細に分析されます。このようなビームを焦点の近くで使用すると、2種類のナノ粒子をトラップすることが期待できます。
はじめに
スパイラル位相因子exp(imθ )過去20年間、 m で大きな注目を集めてきました。 はトポロジカル電荷であり、任意の整数値およびθにすることができます。 は、光軸を横切る平面上の方位角です[1、2]。渦ビームは、光ピンセット[3,4,5,6,7]、自由空間光通信[8]など、「ドーナツ」強度プロファイルと軌道角運動量(OAM)により、多くのアプリケーションで広く使用されています。および量子情報[9]。最近、研究者は、その独特の特性[10,11,12,13,14,15]のために、円偏光渦ビームの研究にもっと注意を向けています。たとえば、それはスピン角運動量(SAM)とOAMの両方を持っています。同時。これらの独自の特性により、渦ビームの用途を大幅に拡大および強化できます。
高NAのレンズシステム下でのさまざまなビームの密集特性は、粒子トラップ[21]、顕微鏡[22]、光学データストレージ[23]での重要なアプリケーションのもう1つのホットトピック[16、17、18、19、20]です。これまで、スカラー渦ビームからベクトル渦ビームまで、さまざまなビームが研究されてきました[10、24、25、26、27、28、29、30、31]。たとえば、Hao etal。 [26]およびPuetal 。 [27]は、高NAレンズの下でらせん状に偏光した渦ビームの特性を研究しました。フラットトップ(FT)プロファイルを実現でき、焦点面で適切な偏光状態を選択することでOAMを調整できることが示されました。 Zhan etal。円偏光を伴う密集した渦ビームの特性を研究し[10]、強い縦成分を生成できることを示しました。
最近、遠方場でエレガントなラゲールガウスビームに進化することができる新しいビームである異常渦ビーム(AVB)が提案されました[32]。そのようなビームは、その並外れた伝搬特性のために多くの注目を集め、広く研究されてきました[33,34,35,36,37,38]。私たちの知る限り、高NAレンズによって焦点を合わせられたCPAVBに関する報告はありません。この論文では、タイトフォーカス後のCPAVBの数式が導き出されます。次に、ビームの次数、トポロジカル電荷、およびNA値がビームプロファイルと位相分布に与える影響を分析します。最後の部分では、密集したCPAVBの光学力が研究されます。
メソッド
円偏光ビームは次のように書くことができます。これは、放射状および方位角方向に偏光されたビームの線形重ね合わせを示します[10]:
$$ {\ mathrm {E}} _ {LHC(RHC)} =P(r){e} ^ {\ pm i \ varphi} \ left({\ mathrm {e}} _ {\ rho} \ pm j {\ mathrm {e}} _ {\ varphi} \ right)/ \ sqrt {2} $$(1)ここで P ( r )は振幅分布です。記号「+」と「-」は、それぞれ左側と右側の円偏波です。 e ρ および e φ は、それぞれ円筒座標の半径ベクトルと方位角ベクトルです。また、放射状および方位角方向に偏光されたビームの表現は、[39,40,41]で取得できます。
フォーカシングシステムのスキームは、参考文献と同じです。 [42]。正弦条件( r )でのAVBの瞳孔アポダイゼーション関数 = f sin θ )は[32、38]と書くことができます:
$$ {\ mathrm {E}} _ {\ mathrm {n}、\ mathrm {m}} \ left(\ theta、\ varphi \ right)={E} _0 {\ left(\ frac {f \ sin \ theta} {w_0} \ right)} ^ {2n + \ left | m \ right |} \ exp \ left(-\ frac {f ^ 2 {\ sin} ^ 2 \ theta} {{w_0} ^ 2} \ right )\ exp \ left(-im \ varphi \ right)$$(2)ここで f は焦点距離、θです 0からαまで変化します 、α はNAの最大角度であり、 E 0 および w 0 それぞれ一定のウエスト半径です。 n 、φ 、および m は、それぞれビーム次数、方位角座標、トポロジカル電荷です。
ベクトルデバイ理論によれば、円筒座標で密集したCPAVBの電場の式は、次のように導出できます。 (3):
$$ {\ displaystyle \ begin {array} {l} {E} _ {\ pm、\ rho} \ left(\ rho、\ varphi、z \ right)=-\ frac {ikf} {2} {\ int } _0 ^ {\ alpha} {E} _0 {\ left(\ frac {f \ sin \ theta} {w_0} \ right)} ^ {2n + \ left | m \ right |} \ exp \ left(-\ frac {f ^ 2 {\ sin} ^ 2 \ theta} {w_0} \ right){i} ^ m \\ {} \ kern6.399996em \ times \ sin \ theta \ sqrt {\ cos \ theta} \ exp \ left (ikz \ cos \ theta \ right)\ exp \ left [i \ left(m \ pm 1 \ right)\ varphi \ right] \\ {} \ kern6.399996em \ times \ left [\ left(\ cos \ theta +1 \ right){J} _m \ left(k \ rho \ sin \ theta \ right)-\ left(\ cos \ theta -1 \ right){J} _ {m \ pm 2} \ left(k \ rho \ sin \ theta \ right)\ right] d \ theta \ end {array}} $$(3a)$$ {\ displaystyle \ begin {array} {l} {E} _ {\ pm、\ varphi} \ left(\ rho、\ varphi、z \ right)=-\ frac {ikf} {2} {\ int} _0 ^ {\ alpha} {E} _0 {\ left(\ frac {f \ sin \ theta} { w_0} \ right)} ^ {2n + \ left | m \ right |} \ exp \ left(-\ frac {f ^ 2 {\ sin} ^ 2 \ theta} {w_0} \ right){i} ^ {m \ pm 1} \\ {} \ kern6.399996em \ times \ sin \ theta \ sqrt {\ cos \ theta} \ exp \ left(ikz \ cos \ theta \ right)\ exp \ left [i \ left(m \ pm 1 \ right)\ varphi \ right] \\ {} \ kern6.3 99996em \ times \ left [\ left(\ cos \ theta +1 \ right){J} _m \ left(k \ rho \ sin \ theta \ right)-\ left(\ cos \ theta -1 \ right){J } _ {m \ pm 2} \ left(k \ rho \ sin \ theta \ right)\ right] d \ theta \ end {array}} $$(3b)$$ {\ displaystyle \ begin {array} {l } {E} _ {\ pm、z} \ left(\ rho、\ varphi、z \ right)=-ikf {\ int} _0 ^ {\ alpha} {E} _0 {\ left(\ frac {f \ sin \ theta} {w_0} \ right)} ^ {2n + \ left | m \ right |} \ exp \ left(-\ frac {f ^ 2 {\ sin} ^ 2 \ theta} {w_0} \ right){ i} ^ {m \ pm 1} \\ {} \ kern6.399996em \ times {\ sin} ^ 2 \ theta \ sqrt {\ cos \ theta} \ exp \ left(ikz \ cos \ theta \ right)\ exp \ left [i \ left(m \ pm 1 \ right)\ varphi \ right] \\ {} \ kern6.399996em \ times {J} _ {m \ pm 1} \ left(k \ rho \ sin \ theta \右)d \ theta \ end {array}} $$(3c)ここで J n (α )は n です -第1種の次数ベッセル関数と k =2π/λ。 E を定義します + および E − それぞれ右側と左側のCPAVBの電界の表現として。
上記の式では、次の式が使用されています[43]:
$$ \ left \ {\ begin {array} {l} {\ int} _0 ^ {2 \ pi} \ cos \ left(n \ varphi \ right)\ exp \ left [ia \ cos \ left(\ varphi- \ phi \ right)\ right] d \ varphi =2 \ pi {i} ^ n {J} _n(a)\ cos \ left(n \ phi \ right)\\ {} {\ int} _0 ^ {2 \ pi} \ sin \ left(n \ varphi \ right)\ exp \ left [ia \ cos \ left(\ varphi- \ phi \ right)\ right] d \ varphi =2 \ pi {i} ^ n {J } _n(a)\ sin \ left(n \ phi \ right)\ end {array} \ right。 $$(4)次に、次のように、厳密に焦点を合わせたCPAVBの合計強度を計算できます。
$$ I ={\ left | {E} _ {\ rho} \ left(\ rho、\ varphi、z \ right)\ right |} ^ 2 + {\ left | {E} _ {\ varphi} \ left (\ rho、\ varphi、z \ right)\ right |} ^ 2 + {\ left | {E} _z \ left(\ rho、\ varphi、z \ right)\ right |} ^ 2 $$(5)ここで E ρ 、 E φ 、および E z 対応するコンポーネントの振幅です。
結果と考察
CPAVBのタイトフォーカス特性
このセクションでは、上記の式を使用して、密集したCPAVBの特性を調べます。シミュレーションでは、NA =0.85、λに設定しました。 =632.8 nm、 w 0 =2 mm、および f =2mm。図1では、 n の左側のCPAVBの総強度プロファイルと対応する縦方向および半径方向の成分 焦点面のさまざまなトポロジカル電荷の=1がそれぞれ示されています。 m の場合、中央で合計強度がゼロ以外であることがわかります。 ≤2、 m の場合は中央にダークスポットがあります> 2.さらに、 m の場合、焦点の合ったフィールドの半径方向の成分は軸上でゼロではありません。 =0、2、および m の場合の縦方向成分と同じ =1.これらの結果は、式(1)から説明できます。 (3)と式。 (5)、 J m m を除いて、原点では常にゼロに等しくなります =0. m の場合、3つのコンポーネントすべての第1種ベッセル関数は、中央でゼロになります。> 2、したがって、合計強度はゼロです。それ以外の場合は、 J を含むコンポーネントが少なくとも1つ存在します 0 、これは、中心強度がゼロ以外で最大になる可能性があることを意味します。さらに、総成分と放射状成分の場合、トポロジカル電荷が増加するにつれて焦点スポットのサイズが増加します。したがって、焦点場の総強度と焦点スポットサイズはトポロジカル電荷の影響を受けると結論付けることができます。
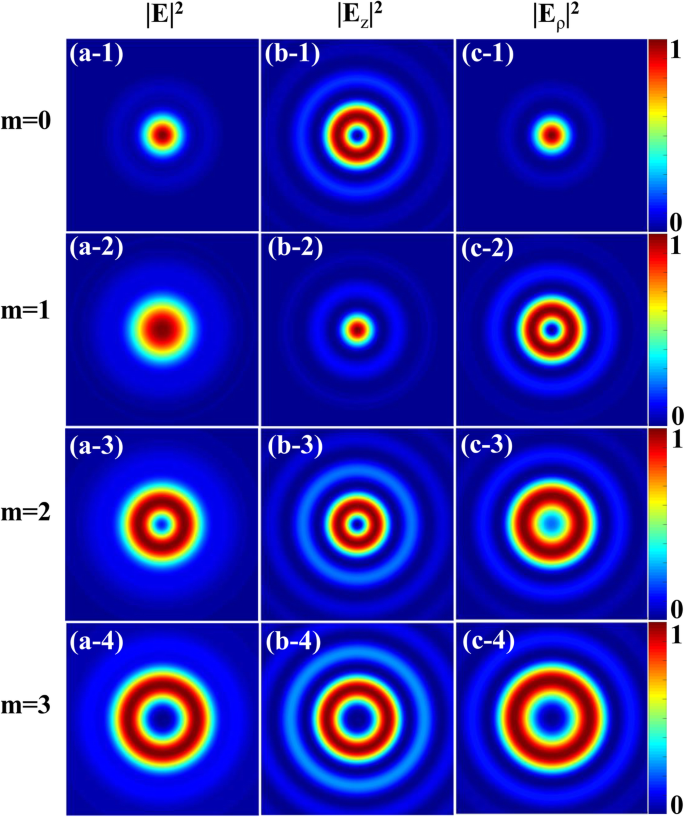
n を使用して密集した左側のCPAVBの強度プロファイル 異なるトポロジチャージの場合は=1。 a-1 a-4 へ 、 b-1 b-4 へ 、および c-1 c-3 へ 総強度です| E | 2 および縦方向| E z | 2 および放射状| E ρ | 2 それぞれコンポーネント
図2では、 m の左側のCPAVBの全強度プロファイルと対応する縦方向および半径方向の成分 焦点面のさまざまなビーム次数の=1がそれぞれ示されています。 n としてそれを見ることができます 増加すると、各成分の外輪と総強度は徐々に明るくなりますが、強度のパターンは変化しません。したがって、ビーム次数 n 強度パターンの形状に大きな影響はありません。
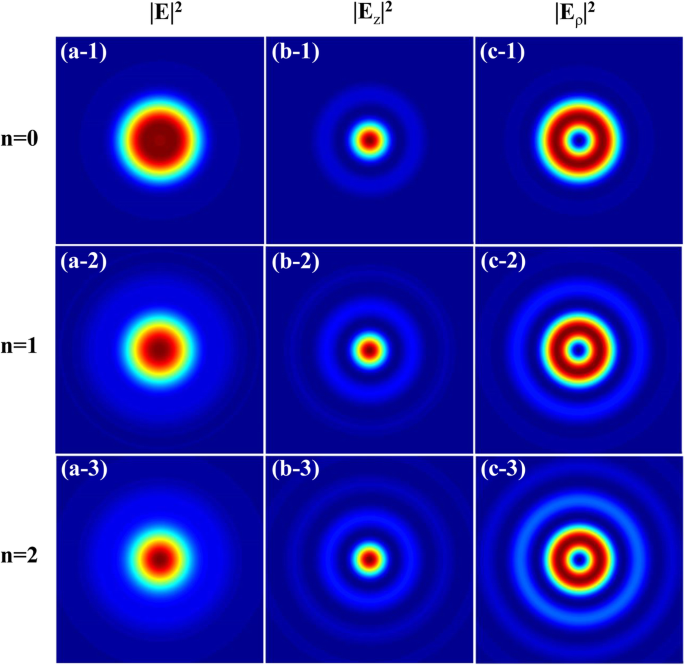
m の密集した左側CPAVBの強度プロファイル 異なるビーム次数の場合は=1。 a-1 a-3 へ 、 b-1 b-3 へ 、および c-1 c-3 へ 総強度です| E | 2 および縦方向| E z | 2 および放射状| E ρ | 2 それぞれコンポーネント
次に、NA値が n のCPAVBの集束特性にどのように影響するかを調べます。 =2 for m =1および m =4それぞれ。図3に示すように、トポロジカル電荷 m の場合、中心強度がゼロ以外のままであることがわかります。 =1、 m の焦点面では中心強度が暗い =4。図3d-1とd-2を比較すると、NAの増加に伴い、強度が増加し、中心に集まることがわかります。特に m の場合 =1、NAが0.8に増加するとFTビームを取得できます。
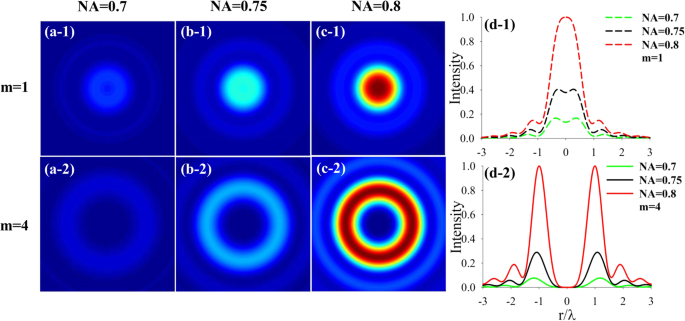
m の左側のCPAVBのNAが異なる場合の強度の変化 =1および m =4それぞれ。 a-1 および a-2 、 b-1 および b-2 、および c-1 および c-2 それぞれNA =0.7、0.75、0.8です。 d-1 および d-2 強度の断面図
式に基づく。 (3c)では、図4に示すように、焦点付近の縦成分CPAVBの位相分布を計算しました。図4の1行目と2行目は、それぞれ左側と右側のCPAVBです。図4a〜cの位置は z です。 =− 0.005 z r 、0、0.005 z r 、それぞれ、ここで z r = kw 0 2 / 2はレイリー範囲です。その他のパラメータは n として設定されます =1およびNA =0.85。図4に示すように、位相パターンの輪郭は、焦点面を通過した後、時計回りから反時計回りに変化します。図4a-1からc-1を図4a-2からc-2と比較すると、左側のCPAVBをaに置き換えると、焦点付近のトポロジカル電荷が3から5に変化することがわかります。右側のもの。この現象は、 m の左側のCPAVBとして説明できます。 =4はSAM l を伝送します s =− ħ およびOAM m =4 ħ 。 SAMから変換された反対のOAMの補正により、トポロジカル電荷はタイトフォーカス後に3に減少します。類推すると、 m を使用した右側のCPAVBと同様の動作が期待できます。 =4、SAM l を伝送します s =ħ およびOAM m =4 ħ 。 SAMから変換されたOAMにより、トポロジ電荷は5に増加します。したがって、厳密に焦点を合わせた後、縦方向のコンポーネントでSAMからOAMへの変換があると結論付けることができます。
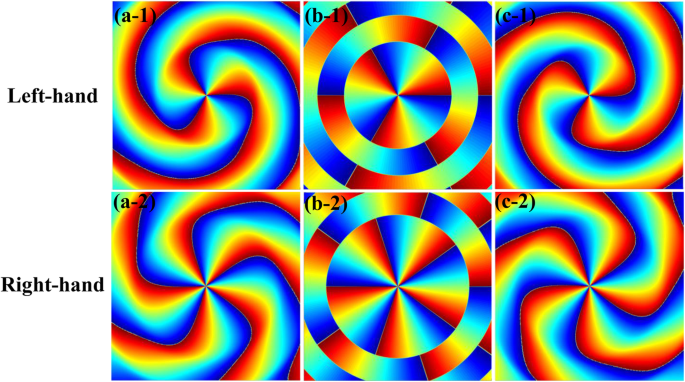
m のCPAVBの縦方向成分の位相プロファイル =4フォーカスの近く。 1行目と2行目は、それぞれ左側と右側のCPAVBです。 a-1 a-2 へ z =− 0.005 z r 。 b-1 b-2 へ z =0。 c-1 c-2 へ z =0.005 z r
密集したCPAVBを使用したナノ粒子の捕捉
レイリー散乱理論[44]に基づいて、光トラッピングを議論する際には、散乱力と勾配力を考慮する必要があります。 F と表記される散乱力 scat = e z n m αI out / c 、光トラップを不安定にする傾向があります。ここで、 c 光速、 e z z に沿った単位ベクトルです 方向、私 out 集束ビームの強度、α =(8/3)π ( ka ) 4 a 2 [(η 2 − 1) 2 /(η 2 + 2) 2 ]、ɑ はナノ粒子の半径、η = n p / n m 、および n m および n p は、それぞれ周囲の媒体とナノ粒子の屈折率です。そして勾配力( F grad )ナノ粒子を焦点に戻す傾向。これはF grad として表すことができます。 =2 πn m β ∇私 out / c 、ここでβ = a 3 (η 2 − 1)/(η 2 + 2)。
シミュレーション実験では、 n を設定しました p =1.59および n p =1ガラスと気泡の場合、それぞれ n m =1.332、NA =0.85、およびɑ =50nm。図5は、 n のナノ粒子に対する左側のCPAVBの半径方向の縦方向の勾配力と散乱力を表しています。 p 異なる m の場合は=1 および n 。前の作品は、 m のとき、全体の強度が中央で暗いことを示しています ≥3。したがって、予想どおり、低屈折率のナノ粒子の場合、図5 a〜dに示すように、半径方向および縦方向の勾配力によって常にナノ粒子が焦点に戻ります。勾配力と比較すると、散乱力は非常に小さいです。したがって、低屈折率のナノ粒子を安定してトラップすることができます。
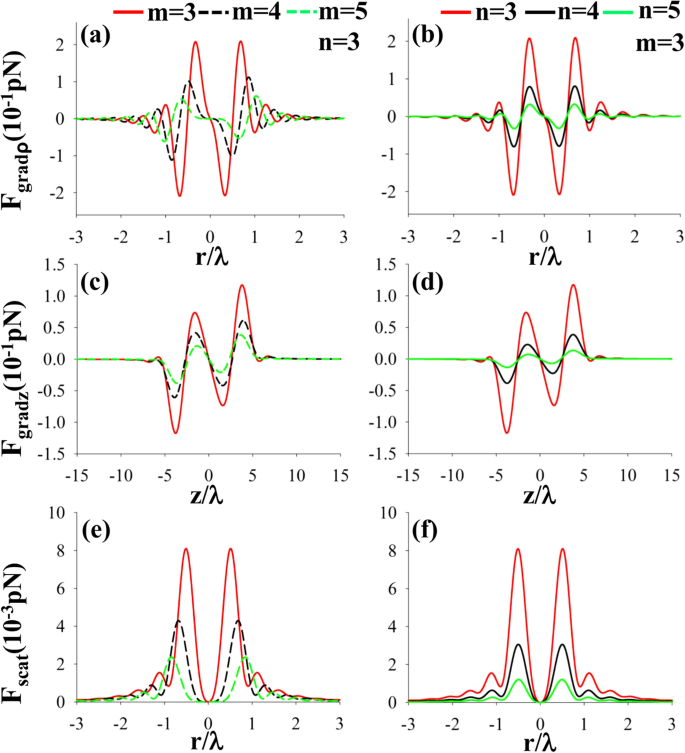
a – f 低屈折率粒子 n にしっかりと焦点を合わせた後の、左側のCPAVBの半径方向の縦方向の勾配力と散乱力 p =1
図6は、 n のナノ粒子に対する左側のCPAVBの半径方向、縦方向の勾配力、および散乱力を表しています。 p =さまざまなトポロジカル電荷 m の場合は1.59 ビームオーダーは n 。図6から、焦点の近くにいくつかの平衡点があり、勾配力と比較して散乱力を無視できることがわかります。したがって、高屈折率のナノ粒子を焦点の近くで捕捉することができます。
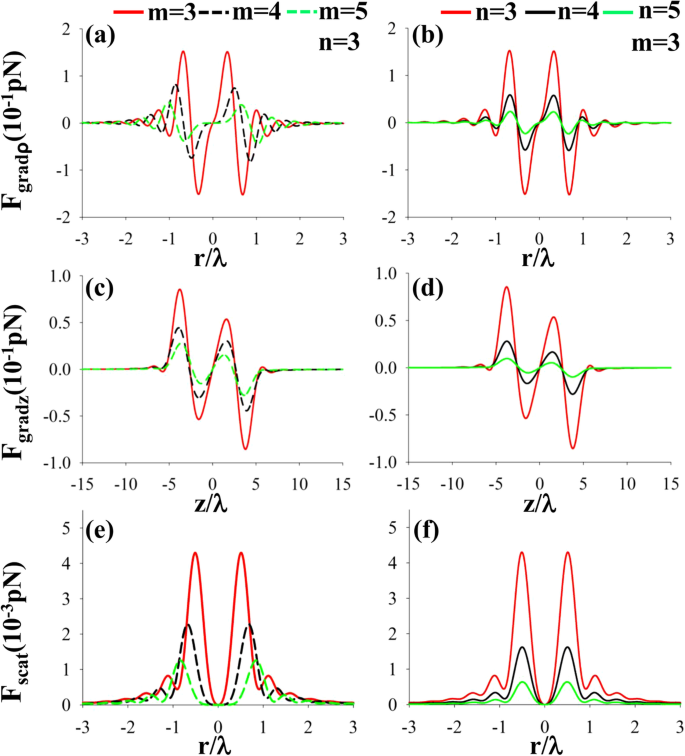
a – f 高屈折率粒子 n にしっかりと焦点を合わせた後の、左側のCPAVBの半径方向の縦方向の勾配力と散乱力 p =1.59
結論
この論文では、密集したCPAVBの特性と、ナノ粒子に対するそれらの光学力について説明しました。 CPAVBのSAMは、このようなビームがしっかりと集束されている場合にOAMに変換できることがわかります。さらに、密集したCPAVBを使用して、焦点面の近くで、低屈折率と高屈折率の2種類のナノ粒子をトラップできます。私たちの研究は、CPAVBの潜在的なアプリケーションを見つけるのに役立ちます。
データと資料の可用性
現在の研究中に生成および/または分析されたデータセットは、合理的な要求に応じて対応する著者から入手できます。
略語
- AVB:
-
異常な渦ビーム
- CPAVB:
-
円偏光異常渦ビーム
- FT:
-
フラットトップ
- NA:
-
開口数
- OAM:
-
軌道角運動量
- SAM:
-
スピン角運動量
ナノマテリアル
- アルミニウムのトップ10の特性とその用途
- 半導体ナノ粒子
- アルミニウムの特性と合金の特性
- コバルトをドープしたFeMn2O4スピネルナノ粒子の調製と磁気特性
- 垂直電場によるML-GaSの電子的および光学的異方性特性の変調
- 小さなセレンナノ結晶とナノロッドの容易な合成と光学的性質
- SrTiO3修飾ルチルTiO2ナノファイバーのワンステップエレクトロスピニングルートとその光触媒特性
- 無電解エッチングで作製したシリコンナノワイヤの光学的および電気的特性
- 高効率偏光ビームスプリッターと光渦発生器のための高次誘電体メタ表面
- In VivoCTイメージングおよび腎クリアランス特性のための新しい生体適合性AuNanostars @PEGナノ粒子
- Al2O3 / ZnOナノラミネートの形態的、光学的、および電気的特性に及ぼす二重層の厚さの影響



