HOTグラフェンおよびHOTグラフェンナノチューブ:新しい低次元半金属および半導体
要約
HOT という名前の新しいグラフェン同素体を報告します 炭素の六角形、八角形、および四角形を含むグラフェン。対応する一連のナノチューブも、 HOT を巻き上げることによって構築されます グラフェンシート。 HOT の幾何学的および電子的構造に対して、abinitio計算が実行されます。 グラフェンと HOT グラフェンナノチューブ。 HOT の非六角形構造で、ディラックコーンと高いフェルミ速度が実現されます。 グラフェンは、ハニカム構造がディラックフェルミオンが存在するための必須条件ではないことを意味します。 ホット グラフェンナノチューブは、そのトポロジーに応じて独特の電子構造を示します。 (0,1) n ( n ≥3) HOT グラフェンナノチューブは半金属の特性を明らかにし、他のナノチューブのセット(1,0) n は、チューブサイズで連続的に調整可能なバンドギャップ(0〜0.51 eV)を示しています。曲率効果とゾーンフォールディング近似の間の競合により、(1,0) n のバンドギャップが決まります。 ナノチューブ。半金属性と半導電性の間の新しい変換は、超小型チューブ(半径<4Å、つまり n )で発生します。 <3)。
はじめに
結合の柔軟性により、カーボンベースのシステムは、同じように多種多様な物理的特性を持つ無制限の数の異なる構造を示します。これらの物理的特性は、大部分、これらの構造の次元の結果です[1]。グラフェンは、六角形の格子構造に結合した炭素原子の単一の2次元層であり[2]、質量のないキャリア、高いフェルミ速度[3]、ディラックコーン[4、5]などの多くのユニークな特性を示します。二次元ディラックフェルミオンの特徴。 2つの等価炭素副格子からなるハニカム格子は、このような興味深い特性を形成する上で重要な役割を果たします[2]。 EnyashinとIvanovskii [6]は、12個の人工2D炭素ネットワークを構築しましたが、グラフェン同素体以外の構造がグラフェンのような電子的振る舞いを示すことはありませんでした。 sp 2 のディラックのようなフェルミ粒子を暗示しているようです。 -結合炭素システムは、ハニカム構造に依存します。下の寸法では、カーボンナノチューブは、直径ナノメートル、長さμmの中空シリンダーに巻かれたハニカム構造です[7、8、9、10]。シートをシリンダーに巻き込む方法は無数にあるため、チューブのキラリティーを定義するさまざまな可能性のあるらせん形状により、直径と微視的構造が異なるナノチューブのファミリーが提供されます[11、12、13]。電子特性と輸送特性は確かにカーボンナノチューブの最も重要な物理的特性の1つであり、直径とキラリティーに大きく依存します[14、15、16、17、18]。グラフェンナノチューブは、半金属[14]または半導体[19,20,21]のいずれかであり、バンドギャップは直径とキラリティーに応じて0から10分の数eVまで変化します[10、14、16]。さらに、半導体チューブのバンドギャップは、チューブの直径に単純に関連していることを示すことができます。半金属ナノチューブは、質量のないキャリア、高いフェルミ速度[22]、ディラックコーン[23]などのグラフェン独自の特性も維持します。このような注目すべき結果は、グラフェンシートの電子特性の知識に基づくいわゆるバンドフォールディングアプローチから、半経験的タイトバインディングアプローチを使用したナノチューブの直接研究まで、さまざまな考察から得ることができます[14、 16、18、23]。より洗練されたabinitio計算と利用可能な実験結果との比較、曲率効果などのより細かい考慮事項、 k F シフト[24、25]、σ-πハイブリダイゼーション[26]が導入されています。グラフェンおよびグラフェンのような材料[6]は、次世代の高速電子無線周波数論理デバイス[27、28]、熱および導電性強化複合材料[29、30]、触媒[31]、センサー[32、33、34、35]、透明電極[27、36]など、上記のすべての異常な特性に基づいています。過去数十年にわたって、カーボンナノチューブは、その並外れた電子的、機械的、および構造的特性のために、論理回路、ガス貯蔵、触媒作用、およびエネルギー貯蔵においても大きな可能性を示してきました[37、38、39]。したがって、新しい炭素同素体(2Dおよび1Dを含む)の作成は、それらの基本的な科学的および技術的重要性のために、多くの理論的および実験的調査の焦点となっています[40]。しかし、現在の実験技術を通じてこれらの刺激的な炭素相の構造を完全に明らかにすることは、それらの量が限られていること、および他の相の混合物のために、通常は非現実的です。理論的な予測が必要であり、大きな成功を収めています[31,32,33,34,35、40,41,42]。
この研究では、専ら六角形の構造を持たない2次元のディラックフェルミオンを持つグラフェンの新しい同素体を設計しました。新しい同素体は、織り交ぜられた炭素の六角形、八角形、および四角形で構築され、 HOT と名付けられました。 グラフェン。 ホット グラフェンナノチューブも HOT を巻き上げることによって構築されました さまざまな方向と一緒にグラフェンシート。電子特性、曲率効果、 k F HOT のシフト効果など グラフェンとナノチューブは、密度汎関数理論(DFT)に基づくabinitio計算を使用して計算されました。
計算方法
HOT に関する現在の計算 グラフェンと HOT グラフェンナノチューブは、密度汎関数理論(DFT)に基づく第一原理法と、Perdew-Burke-Ernzerh(PBE)交換相関汎関数[43]の形式の一般化勾配近似(GGA)を使用して実行されました。ウィーンAbinitioシミュレーションパッケージ(VASP)[44、45]に実装されています。波動関数は、520eVの平面波運動エネルギーのカットオフまで平面波で拡張されました。ブリュアンゾーン(BZ)積分は、 k を使用したMonkhorst-Pack [46]サンプリングスキームを使用して実行されました。 -2π×0.03Å − 1 のポイントメッシュ解像度 。ユニットセルの基底ベクトル(ユニットセルの形状とサイズを表す)と原子座標は、すべての原子にかかる力が0.01 eV /Åより小さくなるまで、各システムで完全に緩和されました。
結果と考察
HOT の幾何学的および電子的構造 グラフェン
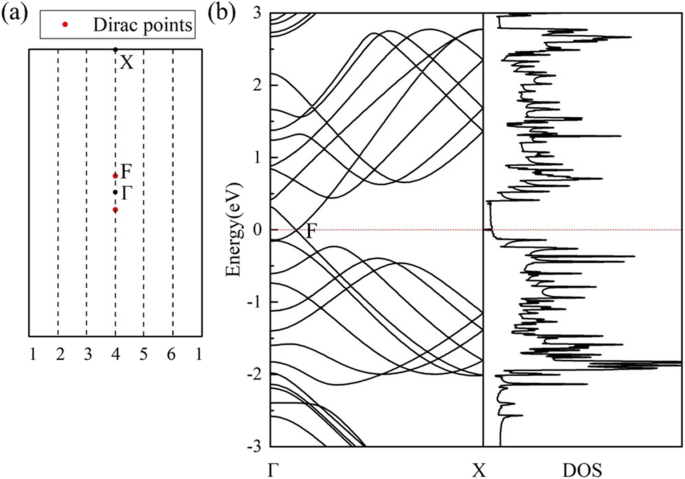
HOT の幾何学的構造 グラフェン(図1a)は、グラフェンよりも複雑な結合状況を示しています。 HOT のさまざまなカーボンポリゴン グラフェンは、さまざまな炭素結合特性をもたらします。 HOT のこれらのポリゴン グラフェンは互いに共通のエッジを共有しており、結合はそれらが属する2つのポリゴンによって区別できます。したがって、私たちの研究では、それらは6–8結合、4–8結合、4–6結合、6–6結合、および8–8結合と呼ばれています。 4–8結合と6–8結合には、2つの異なる結合長があります。4–8結合の場合は1.44Åと1.47Åです。 6〜8の結合の場合は1.41Åおよび1.48Å。 4–6結合、6–6結合、および8–8結合は、それぞれ1.44Å、1.46Å、および1.34Åの固有の結合長を持っています。図1bは、 HOT のバンド構造と状態密度(DOS)を示しています。 図1cに示されている対応するBZを持つグラフェン。フェルミ準位でのエネルギーバンドの交差点は、 HOT の半金属性を示しています グラフェン。これは、フェルミ準位でのDOSの消失によって確認されています。ディラック点は、Γに隣接する(0、0.0585、0)にあります。 3Dバンド構造(図2)は、フェルミ準位の近くのバンド表面を示しています。ここでは、上下の円錐面がフェルミ面の2つのディラック点で合流することによって形成されたディラック円錐を見ることができます。対応するフェルミ速度(v F )バンド構造の線形分散の勾配から評価されたディラックフェルミオンのは、6.27×10 5 です。 m / s、8.1×10 5 より少し低い グラフェンナノチューブの場合はm / s [22]、8.6×10 5 グラフェンの場合はm / s [47、48]。高いv F HOT でのキャリアの高い移動性を意味します グラフェン。
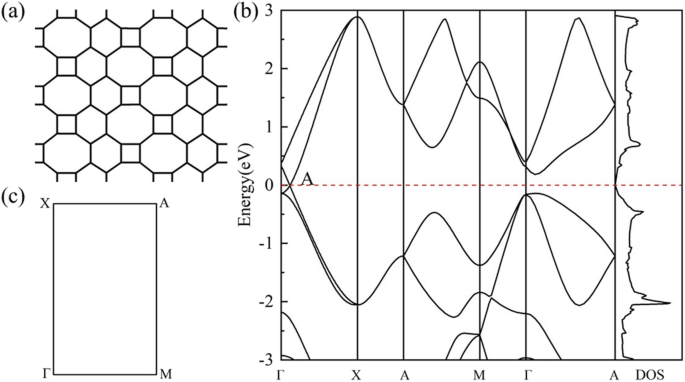
( a ) HOT のジオメトリ グラフェン; ( b ) HOT のバンド構造とDOS グラフェン; ( c ) HOT の対応するBZ グラフェン
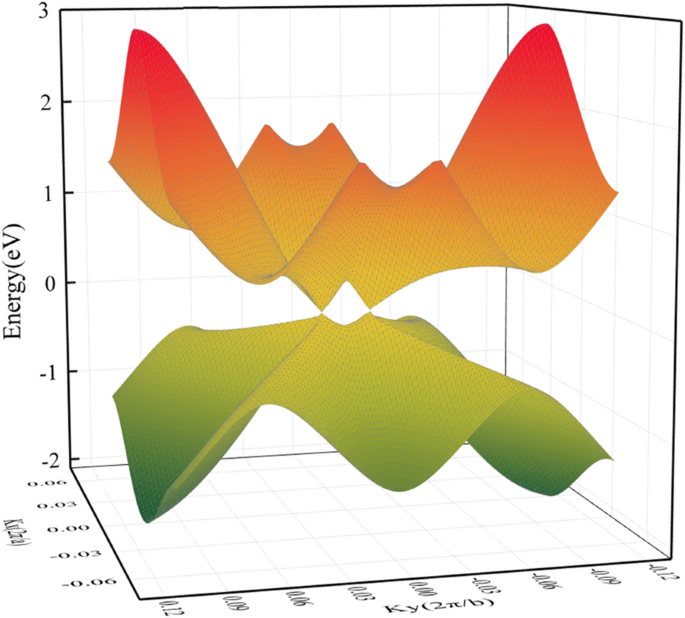
HOT の3Dバンド構造 グラフェン
HOT の幾何学的および電子的構造 グラフェンナノチューブ
HOT グラフェンチューブは HOT から巻き上げられます 2D HOT のインデックスで表されるさまざまな方向のグラフェンシート グラフェン格子(図3a)。このインデックスは( l、m ) n 2つの単位ベクトルに基づく a および b 。記号( l、m )[18、20、21]は、 HOT のさまざまな方向を表します グラフェンシート、 n は、チューブの巻き上げに使用される周囲単位の数(図3bおよびc)を表します。 HOT の空間反転対称性の下で グラフェンユニットセル、ナノチューブシンボルは0≤ l に制限されます および0≤ m 多対1の対応を避けるため。 HOT の可能な幾何学的構造の数 グラフェンナノチューブは、直径と圧延方向の両方に無限の選択肢があるため、無限です。このような多数のナノチューブの中で、私たちの研究では2つの方向(0,1、1,0)のみが選択されています。これは、他の方向への原子のらせん配列がほとんど周期的ではなく、チューブ軸に沿ってほぼ無限の長さのユニットセルを持っているためです。このような大きなユニットセルは、私たちの計算では非現実的です。 (1,0) n 間の異なるローリング方向 および(0,1) n チューブは、形状と結合状況に違いをもたらします。 2つのチューブ(1,0)6と(0,1)4を図3dとeに示し、2つの回転方向の幾何学的な違いを説明します。 (1,0)方向に沿ったポリゴンの配置は、次の2つのパターンに分けることができます。C 4 –c 6 –c 8 (オレンジ)とC 8 –c 6 –c 4 (青)正反対です。これらの2つの反対のパターンは、チューブの円周方向に沿って交互になります。方向(0,1)では、チューブ軸に沿って配置されたポリゴンにも2つのパターンがあります。C 4 –c 8 (青)とC 6 –c 6 (オレンジ)。 2つのC 4 –c 8 パターンは1つのC 6 と交互になります –c 6 円周方向に沿ったパターン。
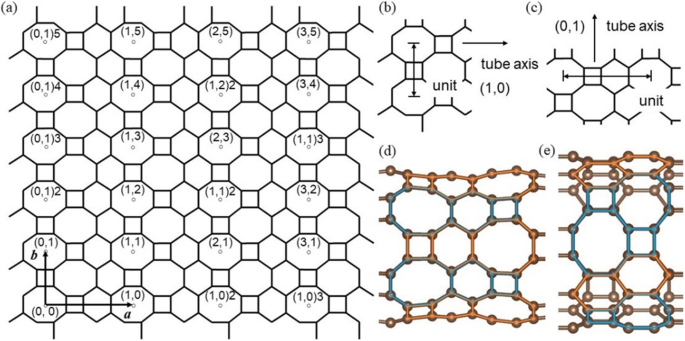
( a )異なるチューブは記号( l、m )で示されます ) n 、with( l、m )は、単位ベクトル a に基づくローリング方向を表します および b 、および n チューブ直径単位の数; ( b )(1,0)方向の直径単位。 ( c )(0,1)方向の直径単位。 ( d )(1,0)6 HOT の幾何学的構造 グラフェンナノチューブ; ( e )(0,1)4 HOT の幾何学的構造 グラフェンナノチューブ
シートをチューブに巻き上げる際のエネルギーコストを明らかにするために、曲率エネルギーを定義します(図4) E cur として:
$$ {E} _ {\ mathrm {cur}} ={E} _ {\ mathrm {tube}} ^ {\ mathrm {at}}-{E} _ {\ mathrm {sheet}} ^ {\ mathrm { at}} $$ここで、\({E} _ {\ mathrm {tube}} ^ {\ mathrm {at}} \)はナノチューブ内の原子の平均エネルギーであり、\({E} _ {\ mathrm {sheet}} ^ {\ mathrm {at}} \)は、2Dシート内の原子の平均エネルギーです。 (1,0) n チューブはグラフェンナノチューブよりもエネルギーコストが低く、(0,1) n チューブは、いくつかの超小型チューブを除いて、アームチェアグラフェンナノチューブとほぼ同じです。このような結果は、 HOT を合成できることも示唆しています。 実験におけるグラフェンナノチューブ。チューブ(1,0)1は、直径がカーボンの結合長よりもさらに短いため、小さすぎることに注意してください。
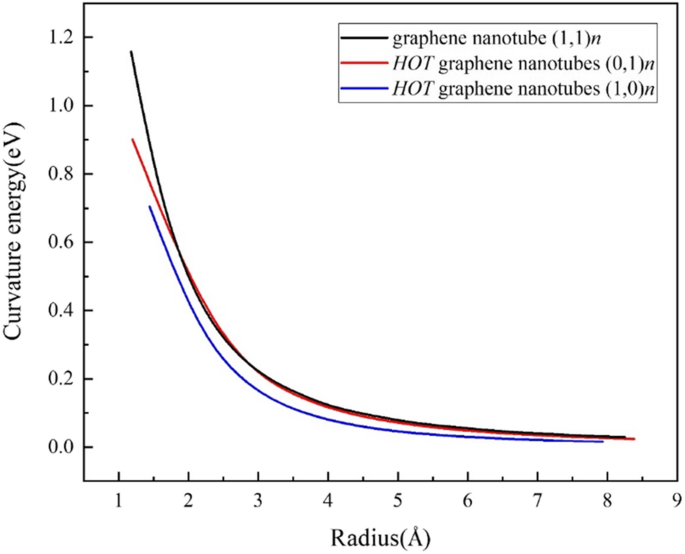
HOT の曲率エネルギー グラフェンナノチューブとグラフェンナノチューブ
計算されたナノチューブ(0,1)6の電子バンド構造とDOS(図5b)は、半金属の特性を示しています。 HOT のとき グラフェンシートはナノチューブに巻き上げられ、ナノチューブの新しい周期境界条件の結果として、その2DBZは1DBZに減少します。チューブの円周方向に沿った周期境界条件は、ナノチューブの円周の「周り」の波数ベクトルのみを許可し、これらのベクトルは量子化されます[49]。ナノチューブ軸に沿った周期境界条件は2Dシートと同じままであり、波数ベクトルはナノチューブ軸に沿って連続したままです。ゾーンフォールディングスキームによれば、特定のナノチューブの電子バンド構造は、特に許可された k に沿った対応する2Dシートの電子エネルギーバンドの重ね合わせによって与えられます。 行[50]。 HOT のBZの中央にある量子化された波数ベクトルとして グラフェンは常にディラック点(図5aの点F)、非縮退ディラック点(図5bの点F)を横切り、ディラックコーンは(0,1) n HOT <のバンド構造に現れます。 / i> グラフェンナノチューブ、すべての(0,1) n の半金属性をもたらします ナノチューブ。チューブ(0,1)6は、この(0,1) n のセットの半金属性を評価するために計算されます。 図5のナノチューブ。(0,1)6 HOT のバンド構造 グラフェンナノチューブはフェルミ準位でエネルギーバンドの交差点を示し、対応するDOSはフェルミ準位で状態を示さず、システムの半金属性を検証します。 (0,1) n のディラックコーンとして チューブは HOT に由来します グラフェンシート、(0,1)6ナノチューブのディラック点の計算された座標は HOT のそれと同じです (0、0.0585、0)であるグラフェンシート。 (0,1)6ナノチューブのディラック点で計算されたフェルミ速度は6.76×10 5 です。 m / s、6.27×10 5 に近い HOT のm / s グラフェンシート。
( a ) HOT の最初のBZ 許可された k のグラフェン (0,1)6ナノチューブの線(破線)。 Fはディラックポイントです。 ( b )(0,1)6ナノチューブの計算されたバンド構造とDOS
(0,1) n のバンド構造の進化 チューブの半径が異なるナノチューブ(図6a)は、 HOT グラフェンナノチューブ(0,1) n 半金属( n ≥3)そして金属に変換します( n =2)その後、半金属に戻ります( n =1)。小さな半径でのこのような変化は、いわゆる曲率効果[26]に起因します。超小型ナノチューブ(例えば、(0,1)2および(0,1)1)の状況では、曲率はゾーンフォールディングスキームに無視できない影響を及ぼします。結合長と結合角は、大きな曲率内で無視できない変化を起こし、電子バンド構造に影響を与えます。そのようなナノチューブのバンド構造は、もはや許可された波数ベクトル上のエネルギーバンドの単純な重ね合わせではありません。この結合の変更により、 k を定義する条件が変更されます。 占有バンドと非占有バンドが交差するポイント( k とラベル付けするポイント F )そして k をシフトします F k と呼ばれる元のディラックポイントから離れて F シフト効果[24、25]。その結果、(0,1) n HOT グラフェンナノチューブ、 k F 元の位置からシフトします( k HOT ) HOT で グラフェンシート(図5aのポイントF)。そして k のシフト方向 F は許容波数ベクトル(図5aの破線)に沿って計算されるため、半金属性は変化しません(図6a( n ) ≥3))。ディラックポイントの計算された調整によると、 k F シフト効果は、チューブ半径5.988Åの(0,1)5で無視できなくなり、そのディラック点( k F )元の点( k )から(0,0.0626,0)にシフトします HOT ) HOT の(0,0.0594,0)で グラフェンシート。チューブの半径が小さくなると、 k F シフトを続け、チューブ(0,1)3のポイント(0,0.0712,0)に到達します。チューブ(0,1)2では、 k F (0,0.0835,0)にシフトし、ディラック点がフェルミ準位より下に移動して、金属系になります。 (0,1)2の半金属性の消失は、 k からの逸脱を示しています。 F (0,1) n のシフト効果 ナノチューブ( n ≥3)。さらに、(0,1)1チューブは、そのバンド構造とDOSで再び半金属になります(図6b)。 (0,1) n HOT の電子状態分析 ナノチューブは、 n でオーバーラップするπ状態を示します ≥2、これは通常、グラフェンナノチューブの半金属性の起源と考えられています[18、24]。ただし、 HOT の対応する電子状態分析 グラフェンナノチューブ(0,1)1は、低位のσ*バンドがフェルミ準位と交差してディラックコーンに結合するσ-π混成軌道を示しています(図6aの青い線)。 (0,0.18345,0)であるディラックポイントの調整も、他の(0,1) n HOT との違いを示しています。 グラフェンナノチューブ。計算されたフェルミ速度は4.47×10 5 です。 m / s、6.27×10 5 未満 HOT のm / s グラフェンシートとその他の(0,1) n の値 ナノチューブ(〜6.76×10 5 MS)。バンド構造の明らかに異なる形状も図6aに示されています。これらすべての文字は、 HOT の半金属性を確認します グラフェンナノチューブ(0,1)1は、σ-π混成軌道に由来します。要約すると、曲率が大きくなるにつれて、 k F シフト効果は n で現れます =5、4≥ n でより効果的になります ≥2であり、最終的に n でσ-π混成効果に置き換えられます =1。
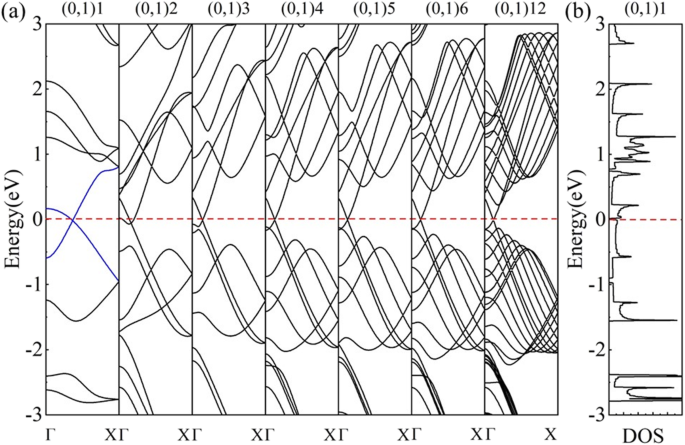
( a )(0,1) n のバンド進化 ナノチューブ( n =1、2、3、4、5、6、12); ( b )(0,1)1ナノチューブのDOS
別の圧延方向では、計算された(1,0)6のバンド構造(図7b)は半導体性を示しています。 6つの波数ベクトル(破線)はΓ-Mに平行で、 HOT のBZの中央にあるГポイントと交差しています。 グラフェン(図7a)、およびDOS(図7b)に示されているように0.46eVのバンドギャップを開きます。このローリング方向では、BZの中央で許可される波数ベクトルにディラック点が含まれることはありません。その結果、このナノチューブのセットにゼロ以外のバンドギャップが生じます。バンドの変化は、図8aの半径が異なるバンドギャップの変化を示しています。 (1,0) n HOT グラフェンナノチューブは半導体です( n ≥4)。価電子帯の最大値(VBM)と伝導帯の最小値(CBM)は、チューブ(1,0)6からチューブ(1,0)4に近づき、半径がチューブ(1,0)3で互いに交差します。 2.17Å。この交差点は、正確に(0.0791,0,0)にあるフェルミ準位にあります。計算されたDOS(図8b)は、フェルミ準位(1,0)3で0の状態を示し、半金属性を確認します。チューブの半径が(1,0)2に減少すると、0.848eVのギャップが再び開きます。 (1,0)2のCBMとVBMは、それぞれΓ点とM点にあり、間接バンドギャップを示しています。このVBMの変化は、(1,0)2の半導体性の起源が異なることを意味します。 (1,0) n HOT のバンドギャップ変化のさらなる研究 グラフェンナノチューブを図9に示します。 n の関数としてのバンドギャップの変化 (3≤ n ≤23)は、バンドギャップがチューブサイズで調整可能であることを示します。また、単調ではなく、チューブサイズがジグザグ形状であるため、バンドギャップの依存性があります(図9の黒い曲線)。 (1,0)15のグローバル最小値は、ゼロバンドギャップを示します。 (1,0)15の半金属性は、バンド構造とDOSによってさらに確認されます(図9g)。ゾーンフォールディングスキームから、ナノチューブのバンド構造は、対応する量子化された k に沿った2Dシートのバンド構造の重ね合わせであることがわかります。 行[50]。したがって、半金属性は、許可された k の少なくとも1つを示します。 線(図7aの破線)は、 n でディラックポイント(図7aの赤いポイント)と交差します =15.それ以外の場合、許可された k の場合 線はディラック点からの距離があります( k HOT )、ナノチューブにバンドギャップが現れます。さらに、 k 間のこの距離 F および k ディラックコーン付近のバンド分散は線形であるため、線はバンドギャップに比例します[25]。 Δk m k 間の最短距離を測定します F および k m 量子数の線 m 。この距離を計算しましたΔk m ディラックポイント間( k HOT )および許可された k HOT の行 グラフェンを作成し、図9のバンドギャップ(黒い線)と一緒にプロットします(赤い線)。まず、許可されているすべての k 線の量子数は m 。 n の場合 ≤7(例:図9a)、最短距離(Δk m )は k の間にあります HOT そして最初の k 行、 k 1 、は常にΓ点にあります(図9のグラフ(a)を挿入)。この状況では、Δk m 両方の k として一定です 1 および k HOT チューブサイズに関係なく一定です。ただし、許可されている k 大きなナノチューブでは線が密になります(7≤ n ≤17)、 k 2 k に最も近いものになります HOT (例:図9b)。この状況では、 k 2 チューブ半径を大きくして、外側のBZからディラックポイントに近づきます。したがって、Δkの低下を示しています m 図9(7≤ n ≤17)。 n =17は k のターニングポイントです 2 ディラック点とほぼ交差し、距離Δkの極小値になります。 m (図9c)。半径が上がり続けると、 k 2 k をトラバースします HOT ポイントし、それから離れてГポイントに移動し続けると、17≤ n で再び距離が増加します。 ≤24(例:図9d)。同時に、 k 3 ディラックポイントに近づいています。 k 3 k に近づく HOT k より 2 距離の新たな減少を開始しますΔk m n で ≥24。バンドギャップはこの距離に比例するためΔk m [25]、バンドギャップ曲線はΔkと同じ形状を示しています m プロット( n ≥7)。そして、バンドギャップが周期的に変化することが明らかになります: k m ディラックポイントに近づく( k HOT )バンドギャップの減少を引き起こし、次にディラック点を横切って極小値をもたらし、次にディラック点から遠ざかり、バンドギャップの上昇を引き起こし、最後に次の線に置き換えられます k m + 1 次のサイクルに入ります。要約すると、バンドギャップがチューブサイズ( n )によって変化する理由 ≥7)は、 k ラインはさまざまなチューブサイズで移動しているため、距離が変化しますΔk m k の間 HOT 許可された k バンドギャップに比例する線。
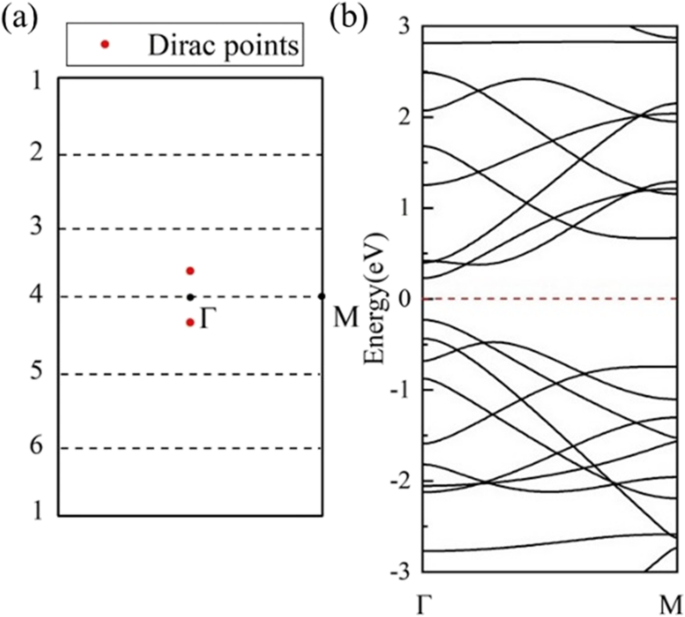
( a ) HOT の最初のBZ 許可された k のグラフェン (1,0)6ナノチューブの線(破線)。 ( b )(1,0)6ナノチューブのバンド構造
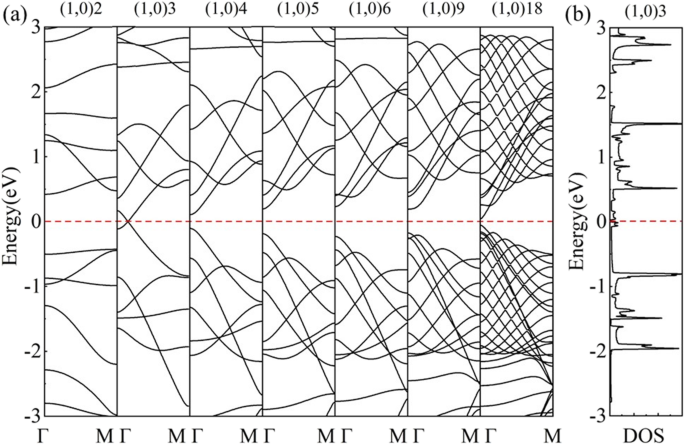
( a ) HOT のバンド進化 グラフェンナノチューブ(1,0) n ( n = 2、3、4、5、6、9、18); ( b )(1,0)3ナノチューブのDOS
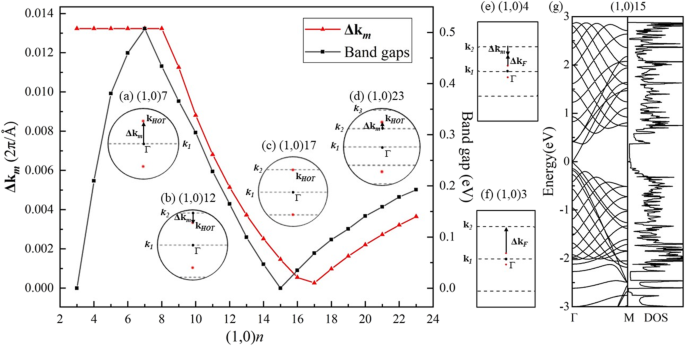
計算されたバンドギャップ(黒い線)と距離Δk m (赤い線) k の間 HOT および最も近い k (1,0) n の行 チューブ。挿入されたグラフは、許可された k のΓ点付近のBZです。 行 k m ( m =1、2、3)(破線)および HOT のフェルミポイント グラフェンナノチューブ k HOT (赤い点)チューブ内( a )(1,0)7、( b )(1,0)12、( c )(1,0)17、( d )(1,0)23、( e )(1,0)4、および( f )(1,0)3。 ( g )チューブのバンド構造とDOS(1,0)15
Δk m 曲線とバンドギャップ曲線の形状は類似しており、両者の違いも明らかです。つまり、Δk m プロットは、 n での変化の「遅延」を示しています ≥7であり、3≤ n でのバンドギャッププロットとは完全に異なります。 ≤7。理由は、 HOT のフェルミポイントが グラフェンナノチューブ( k F )は、 HOT の元のフェルミポイントと同じ座標であると想定されます。 グラフェン( k HOT )前のセクションでバンドギャップの変化について説明しました。ただし、フェルミポイント( k F )ナノチューブでは、原点のフェルミ点( k )から離れてシフトします HOT ) HOT 曲率効果のあるグラフェンシート。したがって、 k F シフト(Δ k F = k F – k HOT )効果は、距離Δk間の不一致に寄与します m とバンドギャップ。 (0,1) n で計算されます チューブ(図6)、 k F (1,0) n チューブはまた、曲率の下で対称点Xに向かって外側のBZにシフトします。したがって、最も近い k m k の間にあります HOT Γ点、距離Δk m バンドギャップを過小評価している(例:17≤ n 図9dの≤24)。それ以外の場合は、最も近い k m k の外側に座っている HOT ポイント、それはバンドギャップの過大評価をもたらします(例えば、7≤ n 図9bの≤17)。小さなナノチューブ(3≤ n ≤7)、 k F 曲率の大きな成長率の下でシフト効果が強化されます。その結果、それは劇的な k を引き起こします F シフトしてバンドギャップを変更します。半径が n より小さくなっているとき =8、 k 1 k に最も近くなります HOT 定数Δkを示します m 。ただし、 k F シフト効果が非常に強いため、 k を動かすことができます F k から遠い 1 しかし、 k に近い 2 (図9e)。 k F シフト効果は k との競争に勝ちます それ以降、線が移動し、バンドギャップの決定を開始します( n ≤7)。 k F k にシフトし続ける 2 k 間の距離が F および k 2 どんどん小さくなっていきます。したがって、(1,0)7から(1,0)3に向かって、バンドギャップは減少します(図9)。最後に、 k F k に追いつく 2 n で交差します =3(図9f)。この k の交差点 k と一致する F 前のセクションで説明したように、チューブ(1,0)3にディラックポイントが生じ、半金属性(図8)が発生します。半径をさらに n に減らします =2は、チューブ(1,0)2に0.848 eVのギャップを開きます(図8)。このギャップは非常に大きく、 k から外れていると見なされます F シフトスキームであるため、図9にはプロットされていません。要約すると、 k の間には競合メカニズムがあります。 ラインの移動と k F バンドギャップを決定する際のシフト。 k F シフト効果は小さなチューブにつながります(7≥ n ≥3)、 k 大きなチューブのライン移動リード( n ≥8)ここで、 k F シフト効果が薄れます。 k の量 F シフトは n で0.00152π/Åと推定されます =15および0.02382π/Å( n ) バンドギャップが0eVであるため=3ここでシフトされた k F ポイントは許可された k にあります 行。 k F シフトは、大きなチューブ(チューブ(1,0)15)よりも小さなチューブ(チューブ(1,0)3)の方が15.86倍大きくなります。
HOT グラフェン、炭素原子はすべて3重に配位しているため、4番目の価電子がその伝導率に重要な役割を果たします。 The calculated band decomposed charge density ± 0.15 eV around the Fermi level (Fig. 10) shows the distribution of the electrons in the Dirac cone. Only the electrons on the 8–8 bonds (Fig. 10a) have an overlapping and the side view (Fig. 10b) shows that the electrons distribute perpendicularly to the HOT graphene sheet, which indicates that the Dirac cone consists of π states. Therefore, the electron overlapping on the 8–8 bonds (enlarged side view in Fig. 10a) is considered to be localized π states. In big nanotubes such as (0,1)6 (Fig. 10c), the charge density is similar to the HOT graphene sheet showing localized π bonds on 8–8 bonds (enlarged side view in Fig. 10c). As the radius decreases to (0,1)2, whose conductivity transforms to metal (Fig. 6), the 8–8 bonds show several deformations (Fig. 10d). Firstly, these states are no longer symmetric with respect to the tube wall. The overlapping of the π state outside the tube wall breaks apart while the π states inside keep overlapping with each other. Besides the 8–8 π bonds, new π bonds form on 4–8 in (0,1)2. These bonds are similar to the deformed 8–8 bonds:separated π states outside the tube wall and overlapping π states inside the tube wall. Every 4–8 bond connects two 8–8 bonds adjacent to it, forming a delocalized π overlapping inside the tube along the tube axis direction. The enlarged side view in Fig. 10d shows the connection between 4 and 8 and 8–8 bonds as a segment of the whole delocalized bond. Therefore, the metallicity in tube (0,1)2 can be attributed to the delocalized π overlapping in the 4–8 and 8–8 bonds along the tube axis direction which provides a pathway for the electrons to travel along the tube. When the radius keeps decreasing, the conductivity disappears and the (0,1)1 tube becomes a semimetal again (Fig. 6). Different from all the other (0,1) n tubes, the 8–8 overlapping (Fig. 10e) in nanotube (0,1)1 is totally broken up; instead, 4–8 overlapping and 4–6 overlapping plays the major role in the Dirac cones. These two bonds belong to two opposite edges in the same carbon tetragons and are arranged parallel to the tube axis. Furthermore, they are no longer π states. Based on the electronic state analysis, a σ-π hybridization takes place at the Fermi level under such a strong curvature in nanotube (0,1)1. It is verified by the charge density which shows the electron states distribute closely to the bond axis (enlarged side view in Fig. 10e). Strongly modified low-lying σ states are introduced at the Fermi level as discussed in the preceding sections (blue line in Fig. 6). Therefore, the σ-π hybrid states in the 4–8 and 4–6 bonds are considered the reason for the semimetallicity in (0,1)1, which is essentially different from the other semimetallic tubes (0,1) n (n ≥ 3). In another set of HOT graphene nanotubes, the band gaps show adjustability with different tube radius (Fig. 9). The charge densities also present an evolution with the tube radii in Fig. 11. The band decomposed charge density of tube (1,0)9 in Fig. 11a and b shows the localized π states overlapping in both the VBM and CBM. The VBM is contributed by π states on 6–6 bonds and 8–8 bonds (Fig. 11a). The CBM is contributed by π states on part of 4–8 and 6–8 bonds (Fig. 11b). The 4–6 bonds have no states on both of the VBM and CBM. When the (1,0) n tubes become semimetallic at some specific radii, such as n = 15, the VBM and CBM meet with each other. Band decomposed charge density ± 0.15 eV around the Fermi level of (1,0)15 nanotube show the different distribution of electrons from the semiconductive tubes. More importantly, it exhibits a similar distribution to the semimetallic HOT graphene sheet and (0,1) n tubes. The localized π bond of (1,0)15 only locates on the 8–8 bonds. This redistribution of electron in (1,0) n tubes causes the conductivity change.
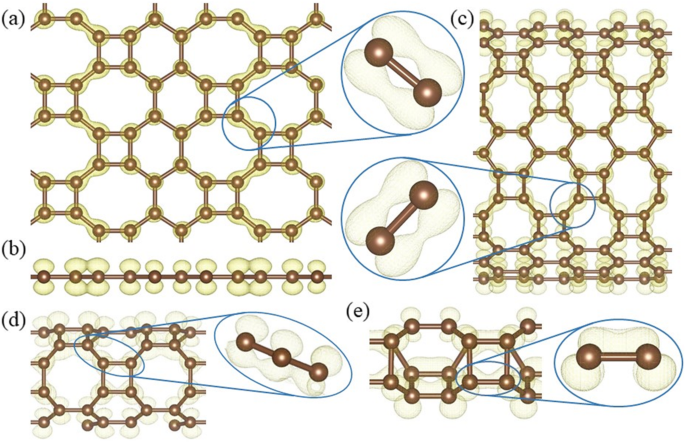
Band decomposed charge densities around the Fermi level of (a ) HOT graphene, (b ) the corresponding side view, and HOT graphene nanotubes (c ) (0,1)6, (d ) (0,1)2, and (e ) (0,1)1 with corresponding enlarged side views
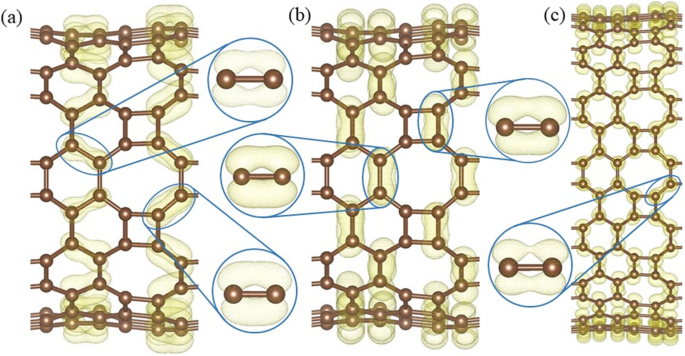
Band decomposed charge densities at (a ) VBM, and (b ) CBM of HOT graphene nanotube (1,0)9; ( c ) charge densities around the Fermi level of the HOT graphene nanotube (1,0)15 with the localized π bond in the enlarged side view
Conclusion
A new graphene allotrope named HOT graphene is constructed by carbon hexagons, octagons, and tetragons showing Dirac cone and high Fermi velocity, which implies that the honeycomb structure is not an indispensable condition for Dirac fermions to exist. The semiconductivity of HOT graphene is dependent on the localized π bonding. A corresponding series of nanotubes is rolled up from the HOT graphene sheet and shows distinctive electronic structures depending on the topology. The set of (0,1) n (n ≥ 3) HOT graphene nanotubes reveals a character of semimetallicity and Dirac cones that are composed by π states. A non-negligible k F shifting along the allowed k line arises under the curvature effect when the tube radius gets smaller (3 ≤ n ≤ 5). However, the ultra-small nanotube (0,1)2 begins to deviate from the π state-based k F shifting effect showing a transformation to metallicity. Finally, an σ-π hybridization takes the place of the π states at Fermi level in nanotube (0,1)1, where a low-lying σ* band intersection appears at the Fermi level and forms a semimetallicity again. Another set of tubes (1,0) n shows various band gaps (0~ 0.51 eV), which is continuously adjustable with the tube size. The band gaps of (1,0) n (n ≥ 3) nanotubes turn out to be determined by a competition mechanism between the k line moving and the k F shifting effect. The zone-folding approximation indicates a k line moving and results in the zigzag and periodical band gap changing curve in big tubes (n ≥ 8), while the k F shifting effect gets stronger and causes a dramatic decrease of band gaps in small tubes (7 ≥ n ≥ 3). Zero-gap semimetallic tubes appear periodically under the competition.
データと資料の可用性
Authors declare that the datasets used and/or analyzed during the current study are available to the readers and included in this article.
略語
- 1D:
-
One-dimensional
- 2D:
-
二次元
- 3D:
-
三次元
- BZ:
-
Brillouin zone
- CBM:
-
Conduction band minimum
- DFT:
-
密度汎関数理論
- DOS:
-
Density of states
- GGA:
-
Generalized-Gradient Approximation
- HOT :
-
Hexagons, octagons, and tetragons
- PBE:
-
Perdew–Burke–Ernzerh
- VASP:
-
Vienna Ab initio Simulation Package
- VBM:
-
Valence band maximum
ナノマテリアル



