簡略化のためのブール規則
ブール代数は、論理回路の単純化に最も実用的です。
論理回路の関数をシンボリック(ブール)形式に変換し、結果の方程式に特定の代数規則を適用して項や算術演算の数を減らすと、簡略化された方程式は、実行する論理回路の回路形式に変換されます。より少ないコンポーネントで同じ機能。
より少ないコンポーネントで同等の機能を実現できれば、信頼性が向上し、製造コストが削減されます。
この目的のために、このセクションでは、式を最も単純な形式に変換するために使用するブール代数の規則がいくつかあります。
この章ですでに確認した恒等式とプロパティは、ブール代数の単純化に非常に役立ち、ほとんどの場合、「通常の」代数の多くの恒等式とプロパティと類似しています。
ただし、このセクションに示されているルールはすべてブール数学に固有のものです。
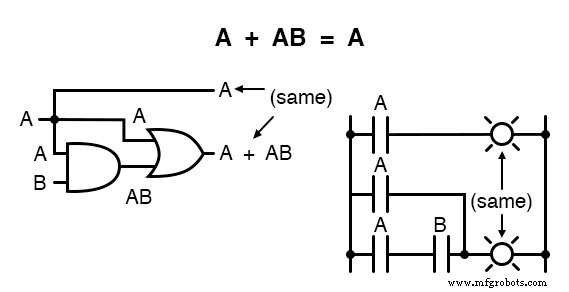
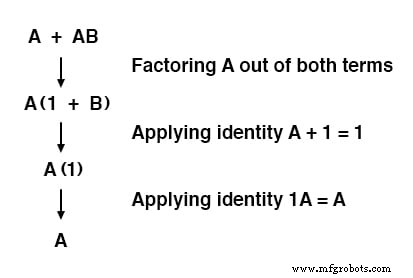
この規則は、2つの項から「A」を因数分解し、A + 1 =1および1A =Aの規則を適用して最終結果を達成することにより、象徴的に証明できます。
ルールA + 1 =1を使用して、(B + 1)項を1に減らす方法に注意してください。
「A + 1 =1」のようなルールが文字「A」を使用して表現されている場合、それが「A」を含む表現にのみ適用されることを意味するわけではありません。
A + 1 =1のようなルールで「A」が表すのは、ブール変数または変数のコレクションです。
これは、ブールの単純化を習得するための新入生にとっておそらく最も難しい概念です。標準化されたID、プロパティ、およびルールを、標準形式ではない式に適用します。
たとえば、ブール式ABC + 1も、「A + 1 =1」の恒等式によって1になります。
この場合、IDの標準形式の「A」用語は、元の表現の「ABC」用語全体を表すことができると認識しています。
次のルールは、このセクションに示されている最初のルールと似ていますが、実際にはまったく異なり、より巧妙な証明が必要です。
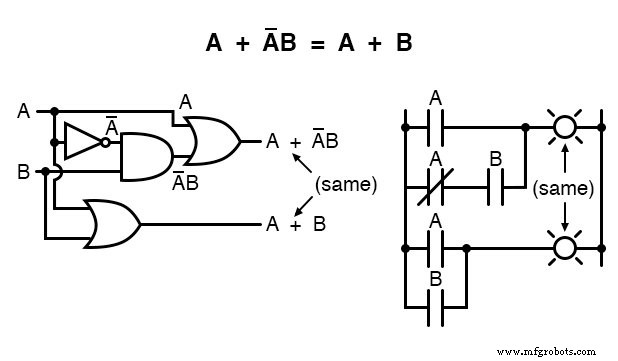
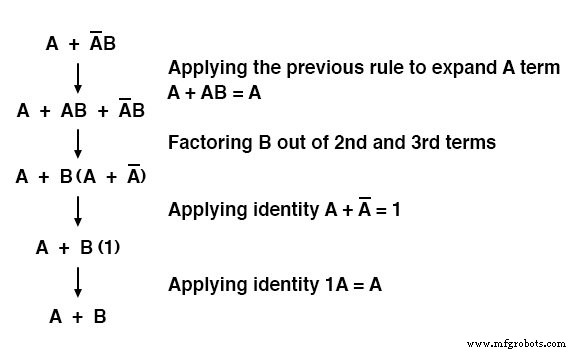
最後のルール(A + AB =A)を使用して、式の最初の「A」用語を「単純化解除」し、「A」を「A + AB」に変更する方法に注意してください。
これは後戻りのように思えるかもしれませんが、表現をより単純なものに減らすのに確かに役立ちました!
数学では、最も洗練されたソリューションを実現するために、「逆方向」の手順を踏まなければならない場合があります。
いつそのような一歩を踏み出すか、いつ踏み出さないかを知ることは、芸術形式の代数の一部であり、チェスのゲームでの勝利には、ほとんどの場合、計算された犠牲が必要です。
もう1つのルールには、和の積の式の簡略化が含まれます。
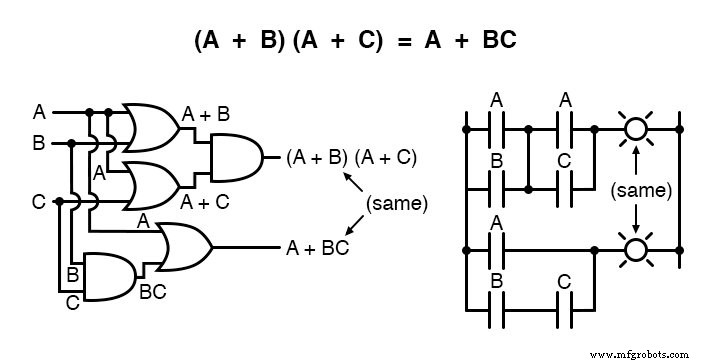
そして、対応する証拠:
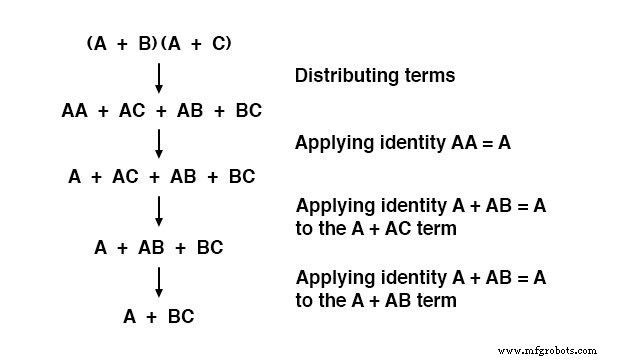
要約すると、このセクションで説明されているブール単純化の3つの新しいルールは次のとおりです。
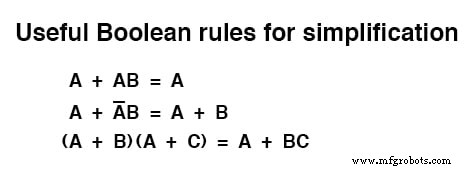
関連するワークシート:
- ブール代数ワークシート
産業技術



