回路の簡略化の例

簡略化が必要な半導体ゲート回路から始めましょう。

「A」、「B」、および「C」の入力信号は、スイッチ、センサー、またはおそらく他のゲート回路から提供されると想定されています。

これらの信号がどこで発生するかは、ゲート削減のタスクでは問題になりません。

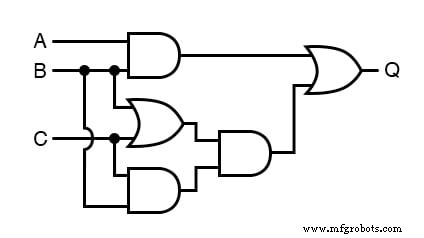
回路を単純化するブール式の書き方

単純化の最初のステップは、この回路のブール式を作成することである必要があります。

このタスクは、各ゲートのそれぞれの入力信号に対応するサブ式を各ゲートの出力に書き込むことから始めれば、段階的に簡単に実行できます。

ORゲートはブール加算に相当し、ANDゲートはブール乗算に相当することに注意してください。

たとえば、最初の3つのゲートの出力に部分式を記述します。

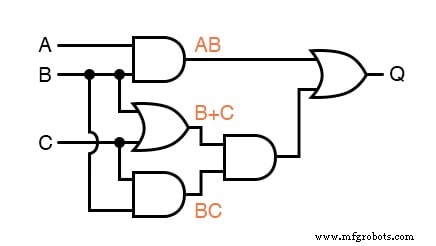
。 。 。次に、次のゲートの別の部分式：

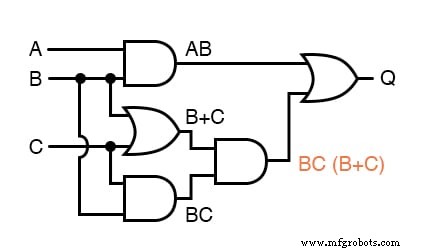
最後に、出力（ "Q"）は式AB + BC（B + C）に等しいように見えます：

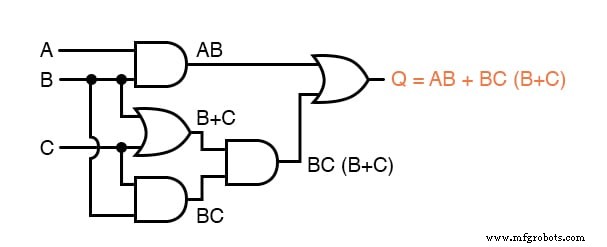
使用するブール式ができたので、ブール代数のルールを適用して、式を最も単純な形式（実装に必要なゲートが最も少ないと定義される最も単純な形式）に減らす必要があります。

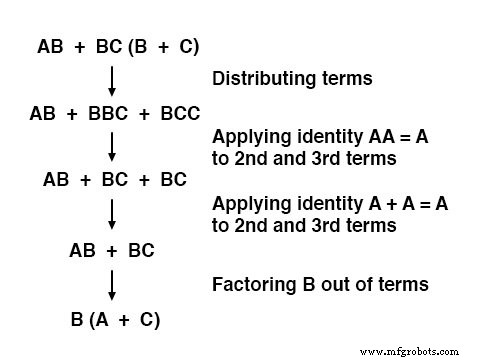
最終的な式B（A + C）は、元の式よりもはるかに単純ですが、同じ機能を実行します。

これを確認したい場合は、両方の式の真理値表を生成し、両方の回路のA、B、およびCの8つの論理状態の組み合わせすべてのQのステータス（回路の出力）を決定できます。 2つの真理値表は同一である必要があります。

ブール式からのスケマティックダイアグラムの生成

次に、このブール式から回路図を生成する必要があります。

これを行うには、演算の適切な数学的順序（加算前の乗算、他の何よりも前の括弧内の演算）に従って式を評価し、各ステップのゲートを描画します。

ORゲートはブール加算に相当し、ANDゲートはブール乗算に相当することを再度覚えておいてください。

この場合、ORゲートであるサブ式「A + C」から始めます。

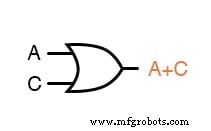
式「B（A + C）」を評価する次のステップは、信号Bに前のゲート（A + C）の出力を乗算（ANDゲート）することです。

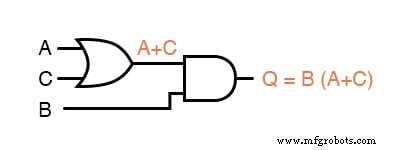
明らかに、この回路は元の回路よりもはるかに単純で、5つではなく2つの論理ゲートしかありません。

このようなコンポーネントの削減により、動作速度が向上し（入力信号遷移から出力信号遷移までの遅延時間が短縮）、消費電力が削減され、コストが削減され、信頼性が向上します。

電気機械式リレー回路にブール単純化を使用する方法

電気機械式リレー回路は、通常、動作するのに低速で、より多くの電力を消費し、より多くのコストがかかり、半導体の対応する回路よりも平均寿命が短いため、ブール単純化の恩恵を劇的に受けます。回路の例を考えてみましょう：

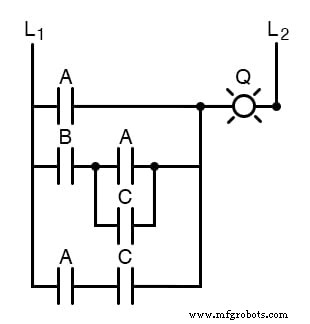
以前と同様に、この回路を最も単純な形式に縮小するための最初のステップは、回路図面からブール式を作成することである必要があります。

これを行うために私が見つけた最も簡単な方法は、通常に従うのと同じ手順に従って、直並列抵抗ネットワークを単一の総抵抗に減らすことです。

たとえば、前の回路のリレー接点と同じ接続パターンで抵抗が配置されている次の抵抗ネットワークと、対応する合計抵抗式を調べます。

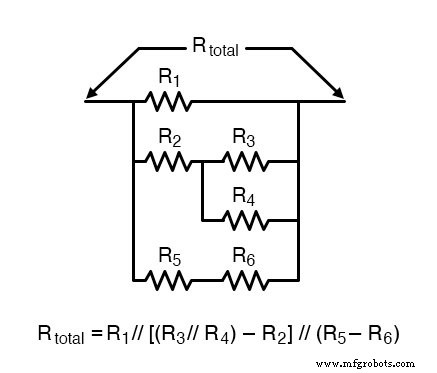
上の図では、抵抗器の直列接続を表すために長いダッシュ記号（—）が使用されています。

並列接点はブール加算に相当し、直列接点はブール乗算に相当することに注意してください。

直並列抵抗ネットワークを総抵抗に減らす場合と同じ優先順位に従って、このリレー接点回路のブール式を記述します。

各ラダー「ラング」の左側にブール部分式を記述して、式の記述を整理するのに役立つ場合があります。

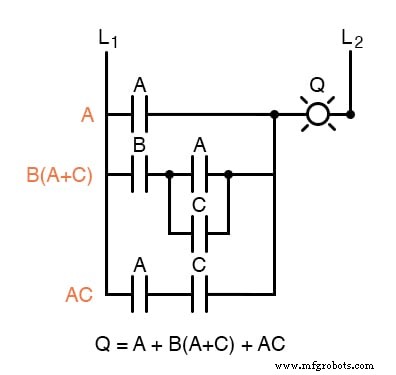
使用するブール式ができたので、ブール代数のルールを適用して、式を最も単純な形式（実装に必要なリレー接点が最も少ないと定義される最も単純な形式）に減らす必要があります。

より数学的に傾いている人は、ルール「A + AB =A」を使用する2つのステップを1つのステップに組み合わせることができ、ルールを「A + AB + AC + AD +」に拡張できることがわかります。 。 。 =A”

ご覧のとおり、縮小された回路は元の回路よりもはるかに単純ですが、同じ論理機能を実行します。

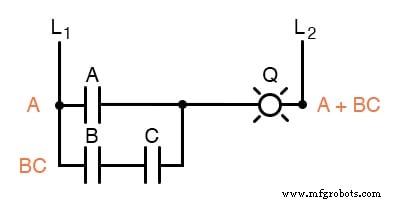
レビュー：

• ゲート回路をブール式に変換するには、最後のゲートで最終式に到達するまで、各ゲート出力にゲートの入力信号に対応するブール部分式のラベルを付けます。
• ブール式をゲート回路に変換するには、標準の演算順序（加算前の乗算、および他の何よりも前の括弧内の演算）を使用して式を評価します。
• ラダーロジック回路をブール式に変換するには、最後のコイルまたはライトで最終式に到達するまで、各ラングに接点の入力信号に対応するブール部分式のラベルを付けます。評価の適切な順序を決定するには、接点を抵抗器であるかのように扱い、それらによって形成される直並列ネットワークの総抵抗を決定しているように扱います。つまり、直接である連絡先を探します。 直列または直接 最初に互いに並行して、次にそれらを同等のブール部分式に「折りたたんで」から、他の連絡先に進みます。
• ブール式をラダーロジック回路に変換するには、標準の演算順序（加算前の乗算、および他の何よりも前の括弧内の演算）を使用して式を評価します。

関連するワークシート：

• Sum-of-ProductsおよびProduct-of-Sums式のワークシート
• ブール代数ワークシート