重ね合わせの原理

重ね合わせの原理は、複雑な主題を取り、それを完全に理にかなっている方法で単純化する天才のストロークの1つです。ミルマンのような定理は確かにうまく機能しますが、理由は明確ではありません。 それはとてもうまくいきます。一方、重ね合わせは明らかです。

シリーズ/並列分析

重ね合わせの原理で使用される戦略は、直列/並列分析を使用して、各電源の変更されたネットワーク内の電圧降下（および/または電流）を個別に決定することにより、ネットワーク内の1つを除くすべての電源を一度に排除することです。次に、別々に動作する各電源の電圧降下および/または電流が決定されると、値がすべて互いに「重ね合わされ」（代数的に加算）、すべての電源がアクティブな状態での実際の電圧降下/電流が検出されます。回路例をもう一度見て、重ね合わせの原理を適用してみましょう。

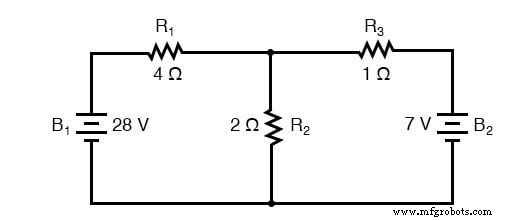
この回路には2つの電源があるため、電圧降下や電流の値を2セット計算する必要があります。1つは28ボルトのバッテリーのみが有効な回路の値です。 。 。

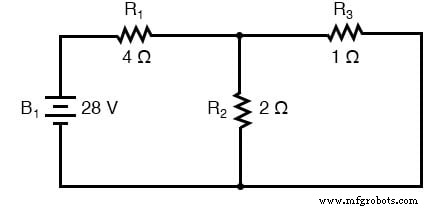
。 。 。 1つは7ボルトのバッテリーのみが有効な回路用です：

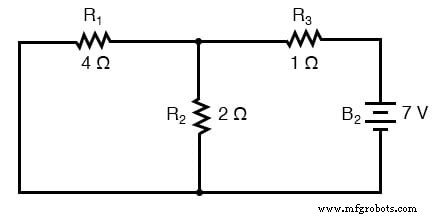
1つの電源で直列/並列解析のために回路を再描画する場合、他のすべての電圧源はワイヤ（短絡）に置き換えられ、すべての電流源は開回路（ブレーク）になります。この例の回路には電圧源（バッテリー）しかないため、分析中にすべての非アクティブな電源をワイヤーに置き換えます。

28ボルトのバッテリーのみで回路を分析すると、電圧と電流について次の値が得られます。

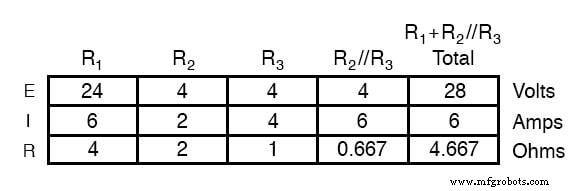
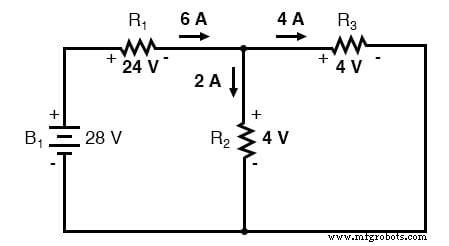
7ボルトのバッテリーのみを使用して回路を分析すると、電圧と電流の別の値のセットが得られます。

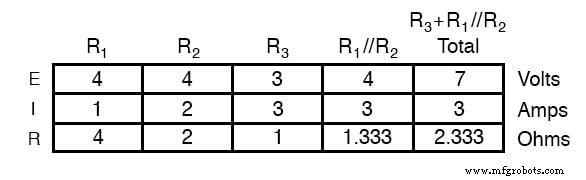
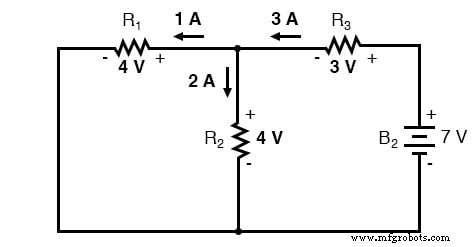
スーパーインポーズによる

これらの電圧と電流の値を重ね合わせるときは、値を代数的に加算する必要があるため、（電圧降下の）極性と（電流の流れの）方向を慎重に考慮する必要があります。 。

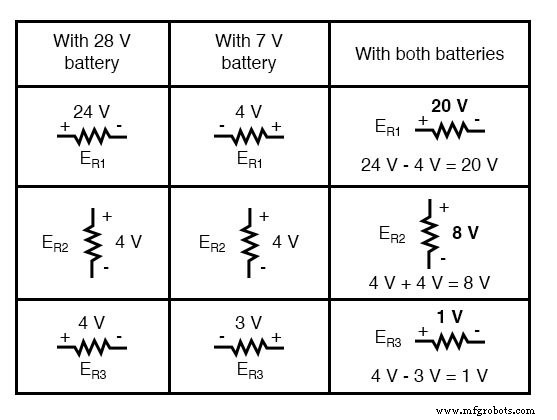
これらの重ね合わせた電圧の数値を回路に適用すると、最終結果は次のようになります。

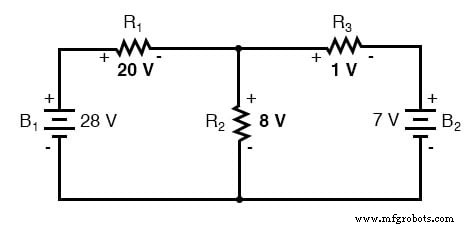
電流も代数的に加算され、抵抗器の電圧降下と同じように重ね合わせるか、最終的な電圧降下とそれぞれの抵抗から単純に計算することができます（I =E / R）。いずれにせよ、答えは同じになります。ここでは、currentに適用される重ね合わせの方法を示します：

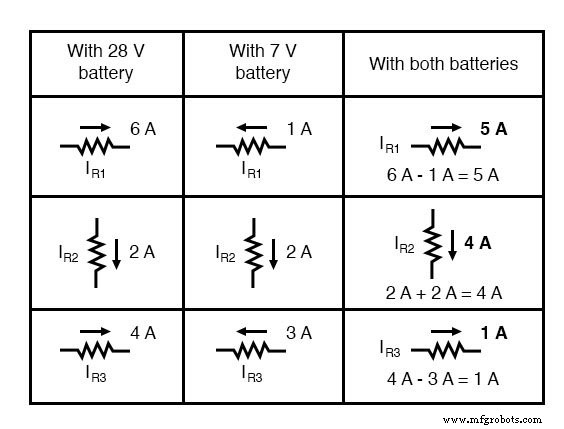
もう一度、これらの重ね合わせた図を回路に適用します：

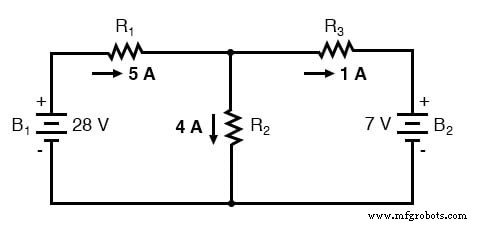
重ね合わせの原理の前提条件

とてもシンプルでエレガントですね。ただし、重ね合わせの定理は、一度に各電源の直列/並列の組み合わせに還元できる回路に対してのみ機能することに注意する必要があります（したがって、この定理は、不平衡ブリッジ回路の分析には役立ちません）。基礎となる方程式が線形である場合に機能します（数学的な累乗や根はありません）。線形性の必要条件は、重ね合わせの原理が電圧と電流の決定にのみ適用可能であり、電力ではない!!! ことを意味します。 非線形関数である消費電力は、一度に1つのソースのみが考慮される場合、代数的に正確な合計に追加されません。線形性の必要性は、コンポーネントの抵抗が電圧または電流によって変化する回路にはこの定理を適用できないことも意味します。したがって、ランプ（白熱灯またはガス放電）やバリスタなどのコンポーネントを含むネットワークは分析できませんでした。

重ね合わせの原理のもう1つの前提条件は、すべてのコンポーネントが「バイラテラル」でなければならないことです。つまり、電子がどちらの方向にも流れる場合でも同じように動作します。抵抗器には極性固有の動作がないため、これまで調査してきた回路はすべてこの基準を満たしています。

重ね合わせの原理は、交流（AC）回路、および半導体（増幅器）回路の研究で使用されます。半導体（増幅器）回路では、ACがDCと混合（重ね合わされる）されることがよくあります。 ACの電圧と電流の方程式（オームの法則）はDCと同じように線形であるため、重ね合わせを使用して、DC電源のみ、次にAC電源のみで回路を分析し、結果を組み合わせてACとACの両方で何が起こるかを知ることができます。有効なDCソース。ただし、今のところ、回路を分析するために連立方程式を実行する必要がないので、重ね合わせで十分です。

レビュー：

• 重ね合わせの原理によると、回路は一度に1つの電源のみで分析でき、対応するコンポーネントの電圧と電流を代数的に加算して、有効なすべての電源で何が行われるかを調べます。
• 分析のために1つを除くすべての電源を無効にするには、電圧源（バッテリー）をワイヤーに交換します。現在のソースをオープン（ブレーク）に置き換えます。

関連ワークシート：

• 重ね合わせの原理ワークシート