ミルマンの定理

ミルマンの定理では、回路は分岐の並列ネットワークとして再描画され、各分岐には抵抗器または直列バッテリ/抵抗器の組み合わせが含まれています。ミルマンの定理は、それに応じて再描画できる回路にのみ適用されます。ここでも、最後の2つの分析方法に使用した回路例を示します。

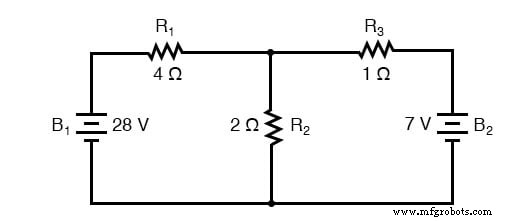
そして、これが同じ回路であり、ミルマンの定理を適用するために再描画されています。

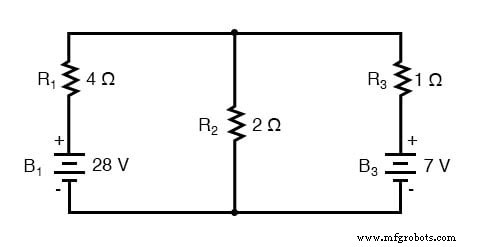
ミルマンの定理は、各分岐内の供給電圧と各分岐内の抵抗を考慮することにより、すべての分岐間の電圧を示します。右端のブランチのバッテリーに「B ₃ 」というラベルを付けていることに注意してください 」は、「B ₂ 」がない場合でも、3番目のブランチにあることを明確に示します。 」回路内！

ミルマンの定理方程式

ミルマンの定理は長い方程式にすぎず、並列接続された分岐のセットとして描かれた回路に適用されます。各分岐には、独自の電圧源と直列抵抗があります。

この式の可変項を回路例の実際の電圧と抵抗の数値に置き換えると、次の式が得られます。

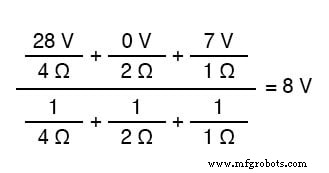
8ボルトの最終的な答えは、次のように、すべての並列ブランチで見られる電圧です。

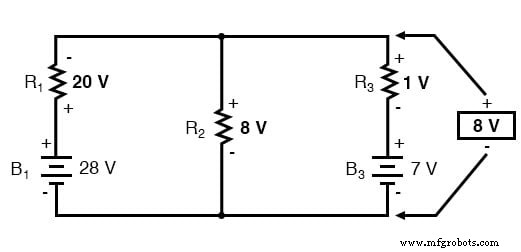
ミルマンの定理のすべての電圧の極性は、同じ点を基準にしています。上記の回路例では、並列回路の下部のワイヤを基準点として使用したため、各分岐内の電圧（R1分岐の場合は28、R2分岐の場合は0、R3分岐の場合は7）をに挿入しました。正の数としての方程式。同様に、答えが8ボルト（正）になったとき、これは回路の上のワイヤーが下のワイヤー（元の基準点）に対して正であることを意味しました。両方のバッテリーが逆方向に接続されていた場合（負の端が上に、正の端が下に）、ブランチ1の電圧は-28ボルト、ブランチ3の電圧は-7ボルトとして式に入力され、結果として-の答えが得られます。 8ボルトは、上部のワイヤが下部のワイヤ（最初の基準点）に対して負であることを示しています。

抵抗器の電圧降下の解決

抵抗器の電圧降下を解決するには、（並列ネットワーク全体の）ミルマン電圧を各分岐内の電圧源と比較する必要があります。直列に追加する電圧の原理を使用して、各抵抗器の両端の電圧の大きさと極性を決定します。

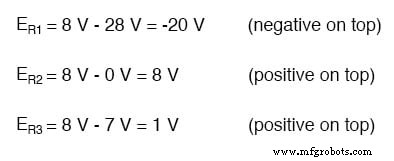
分岐電流の解決

分岐電流を解決するために、各抵抗器の電圧降下をそれぞれの抵抗器で割ることができます（I =E / R）：

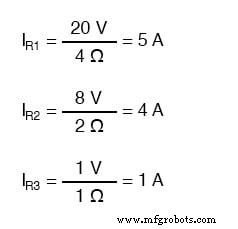
電流の方向を決定する

各抵抗器を流れる電流の方向は、各抵抗器の極性によって決まります。 B ₃ の場合のように、電流をバッテリーに強制的に戻すことができるため、各バッテリーの極性によって異なります。 例の回路では。ミルマンの定理は、分岐電流またはメッシュ電流の方法ほど「間違った」電流方向を直接示すものではないため、これを覚えておくことが重要です。キルヒホッフの電圧法則によって与えられる抵抗器の電圧降下の極性に細心の注意を払い、そこからの電流の方向を決定する必要があります。

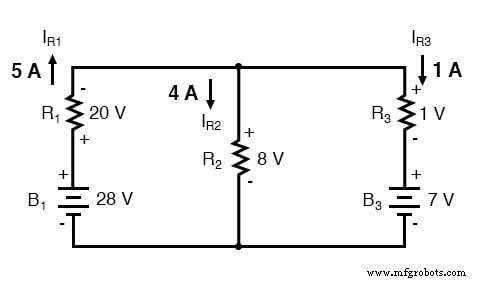
ミルマンの定理は、一連の並列分岐の両端の電圧を決定するのに非常に便利です。ここでは、通常の直並列還元法による解決を妨げるのに十分な電圧源が存在します。また、連立方程式を使用する必要がないという意味でも簡単です。ただし、この形式に合わせて再描画できる回路にのみ適用されるという制限があります。たとえば、不平衡ブリッジ回路を解決するために使用することはできません。また、ミルマンの定理を適用できる場合でも、個々の抵抗器の電圧降下の解法は、一部の人にとっては少し気が遠くなる可能性があります。ミルマンの定理の式は、分岐電圧の1つの数値しか提供しません。

ご覧のとおり、各ネットワーク分析方法にはそれぞれ長所と短所があります。それぞれの方法はツールであり、すべての仕事に最適なツールはありません。ただし、熟練した技術者は、整備士がツールボックスに一連のツールを持っているように、これらの方法を頭の中で持っています。装備しているツールが多ければ多いほど、万が一の事態に備えることができます。

レビュー：

• ミルマンの定理は、回路を直列コンポーネントブランチの並列セットとして扱います。
• ミルマンの定理に入力されて解かれるすべての電圧は、回路の同じポイント（通常は並列ネットワークの下部のワイヤ）で極性が参照されます。

関連ワークシート：

• ミルマンの定理ワークシート