補償定理–証明、説明、および解決例
回路解析の補償定理の証明、説明、実験、および解決された例
補償定理
ネットワーク理論の同じ時期に、そのブランチの1つでインピーダンスの変化の影響を知るか研究することが重要です。これは、ネットワークまたは回路の対応する電圧と電流に影響を与えます。補償定理は、ネットワークの変化に関する情報を提供します。
補償定理は、オームの法則の基本概念に基づいて機能します。オームの法則によれば、電流が抵抗器を通過すると、抵抗器の両端である程度の電圧降下が発生します。この電圧降下は、ソース電圧に対抗します。
したがって、追加の電圧源をソース電圧とは反対の極性で接続し、大きさは電圧降下に等しくなります。補償定理はこの概念に基づいて機能します。
補償定理は次のように述べています。
- 関連記事:テブナンの定理。解決例を含むステップバイステップガイド
補償定理の説明
報酬の定理を理解するには、次の図を検討してください。
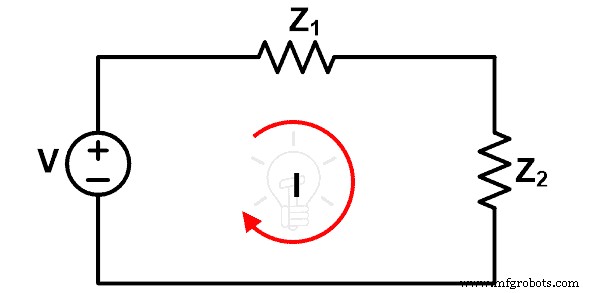
この図では、電圧源Vは独立した電圧源であり、2つのインピーダンスZ 1 およびZ2 線形または両側の要素です。したがって、このネットワークに補償定理を適用できます。ループを通過する電流はIです。
ここで、インピーダンスZ 2を想定します。 ∆Z増加しました。この変更により、ループを通過する電流が変更され、私です。新しい回路図を次の図に示します。
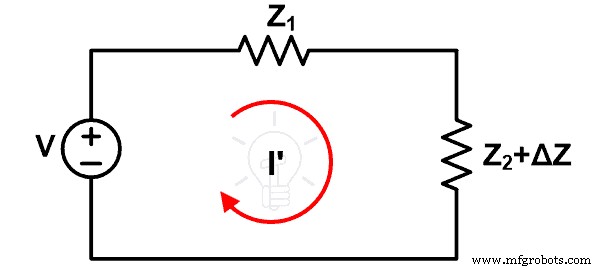
インピーダンスの変化により、ΔIによって与えられる電流の変化。
Δ私 =私 –私
補償定理のステートメントによれば、現在の∆Iの変化を直接計算できます。そのためには、回路を変更する必要があります。
最初の変更は、インピーダンスが変更されたブランチに値IΔZの電圧源を接続することです。そして、この電圧源の極性は主電源と反対です。新しく追加された電圧源VC 補償ソースとして知られています。
V C =私 ΔZ
2番目の変更は、内部インピーダンスによって古い電圧源を削除する必要があることです。理想的な電圧源を考えると、この状態では、端子を短絡することでこの電圧源を取り除くことができます。これらの変更後、残りの回路は次の図のようになります。
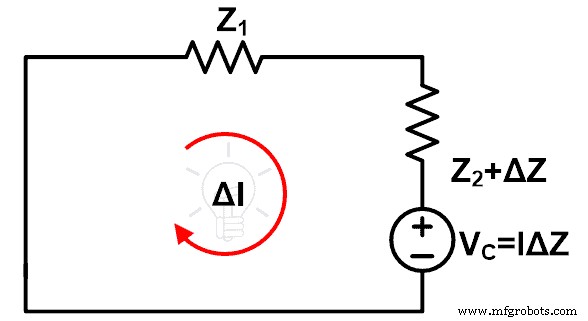
上記の回路を解くことにより、インピーダンスの変化後の電流の変化を簡単に見つけることができます。
- 関連記事:ノートンの定理。解決例を含むステップバイステップガイド
補償定理の証明
図1に示す回路を検討してください。ループを通過する電流(I)を計算します。
KVLをfigure-1に適用します;
ここで、インピーダンスZ 2 ∆Zによって変更されます。また、変更した回路は図2のようになります。図2のループを流れる電流(I’)を計算する必要があります。
図2にKVLを適用します;
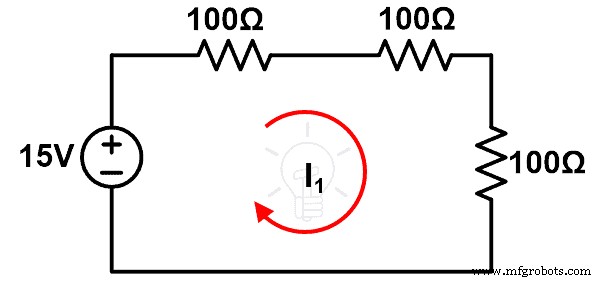
インピーダンスの変化によるループ電流の変化は、ΔIで表されます。そして、ΔIは古い電流Iと新しい電流Iの差に等しくなります。
Δ私 =私 –私
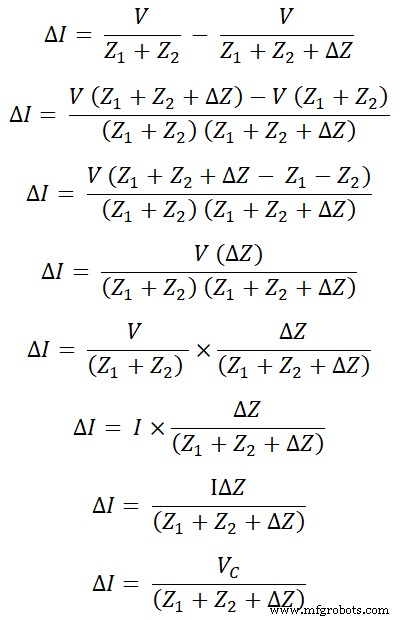
次に、下の図を検討してください。
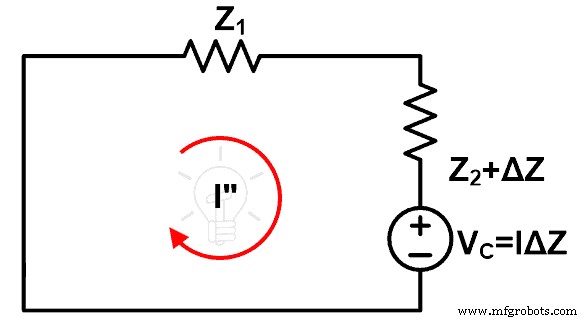
この図は、補償定理の実装後の回路を表しています。ここでは、元の電圧源が短絡によって除去されています(理想的な電圧源を想定しています)。
電流がこのループを通過するのはIです」。そして、この電流を上記で計算された電流と比較します。
ループを通過する電流を計算するには、上の図にKVLを適用します。
V C = Z 1 私」 +( Z 2 +ΔZ ) I”
V C = I” ( Z 1 + Z 2 +ΔZ )
I” =V C /( Z 1 + Z 2 +ΔZ )
I” =ΔI
したがって、修正後の電流の変化(ΔI)は、補償定理によって計算された電流と同じであることが証明されています。
そして、補償定理のステートメントを証明しました。
- 関連記事:重ね合わせの原理–解決された例を使用した回路解析
補償定理の実験
目的: 補償定理を証明し、電流の変化を見つけます。
装置: 電圧計、電流計、抵抗器、接続線、ブレッドボード、
回路図:
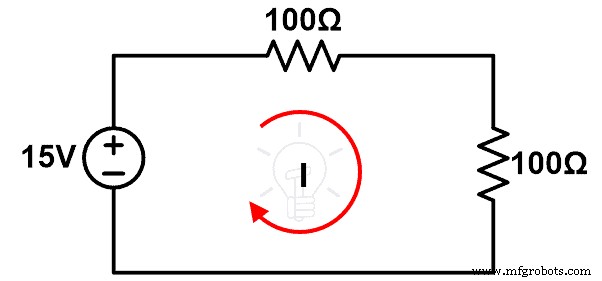

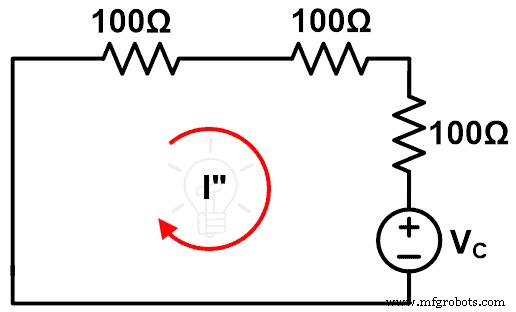
手順:
ステップ-1ブレッドボードの接続ワイヤを使用して、図5に示すようにコンポーネントを接続します。
ステップ2現在のIを測定します。
ステップ-3図-6に示すようにコンポーネントを接続します。ここでは、追加の抵抗を接続しました。
ステップ-4現在のI1を測定します。
ステップ-5 IとI1の値から電流の変化(ΔI)を計算します。
ステップ-6図7に示すようにコンポーネントを接続します。この回路は補償回路です。
ステップ7現在のIを測定する」。
ステップ-8電流の変化(ΔI)をIと比較します。
実験テーブル:
| Sr。いいえ。 | 私 | 私 1 | ∆ I | I” |
| 1 |
結果:
現在のI’’の値を∆Iと比較することで、補償定理を証明できます。
- 関連記事:ミルマンの定理– ACおよびDC回路の分析–例
補償定理の例
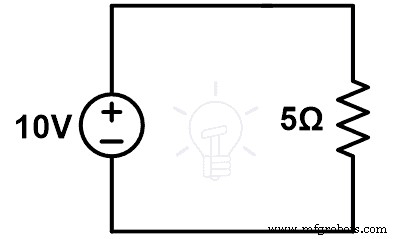
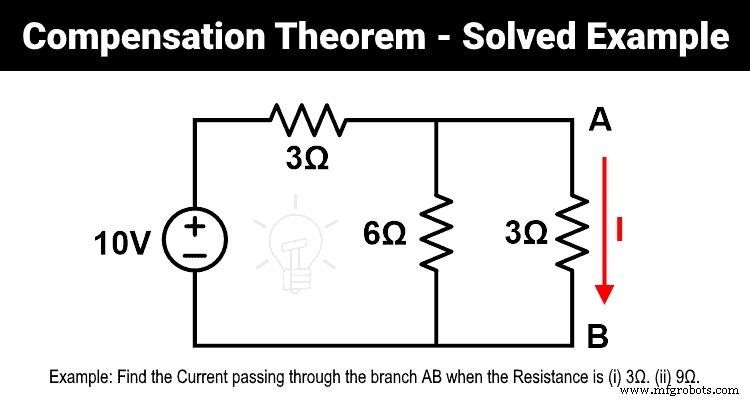
例-1
- 1)抵抗が3ΩのときにブランチABを流れる電流を見つけます。
- 2)3Ωの抵抗が9Ωに変更されたときに、補償定理を使用してブランチABを通過する電流を見つけます。
- 3)補償定理を証明します。
回答-1
図に示すように、6Ωと3Ωの抵抗は並列になっています。そして、この並列の組み合わせは、3Ωの抵抗器と直列に接続されています。したがって、等価抵抗は次のようになります。
R Eq =6 | | 3 + 3
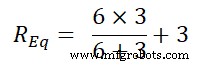
R Eq =2 + 3
R Eq =5Ω

オームの法則によると;
10=私 (5)
私 =10÷5
私 =2 A
次に、ブランチABを通過する現在のパスを見つける必要があります。したがって、現在の分流の法則によれば、
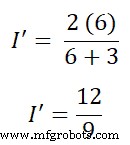
私 =1.333 A(または3/4 A)
- 関連記事:置換定理–解決された例を使用したステップバイステップガイド
回答-2
3Ωの抵抗を9Ωの抵抗に交換する必要があります。補償定理によれば、9Ω抵抗と直列に新しい電圧源を追加する必要があります。そして、この電圧源の値は;
V C =私 ΔZ
場所
ΔZ =9 – 3=6ΩおよびI’ =4/3 A(または1.333 A)
V C =(4 / 3A) x 6Ω
V C =8 V
変更された回路図または補正された回路図は次の図のようになります。
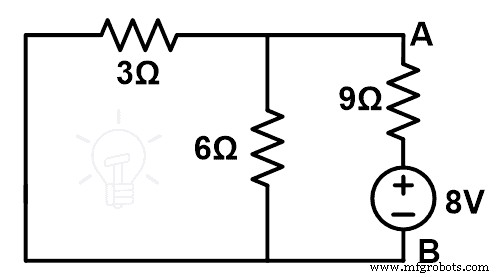
これで、等価抵抗が見つかります。ここでは、3Ωと6Ωの抵抗が並列に接続されています。そして、この並列の組み合わせは、9Ωの抵抗器と直列に接続されています。
R Eq =3 | | 6 + 9
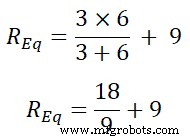
R Eq =2 + 9
R Eq =11Ω
オームの法則に従って、
V =ΔIR
8=ΔI (11Ω)
Δ私 =8÷11
Δ私 =0.7272 A
つまり、補償定理によれば、電流の変化は0.7272Aです。
- 関連記事:テレゲンの定理–解決された例とMATLABシミュレーション
回答-3
補償定理を証明したいと思います。したがって、9Ωの抵抗を使用して、与えられた例の電流を計算します。
変更された回路図を次の図に示します。
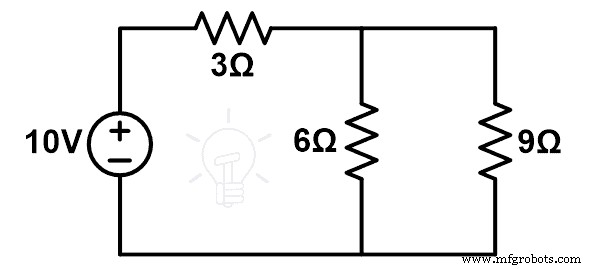
ここでは、9Ωと6Ωの抵抗が並列に接続されており、この並列の組み合わせが3Ωの抵抗と直列に接続されています。
等価抵抗は次のようになります;
R Eq =9 | | 6 + 3
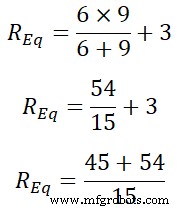
R Eq =99÷15
R Eq =6.66Ω
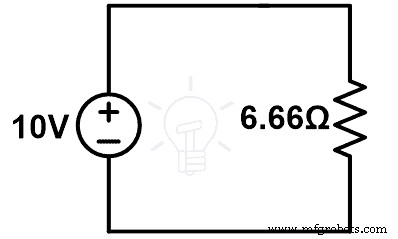
上の図から;
10=私 (6.66)
私 =10÷6.66
私 =1.5151 A
現在の分流の法則による;

I” =0.6060A
Δ私 =私 –私"
Δ私 =(4 / 3A)– 0.6060
Δ私 =1.333A – 0.6060
Δ私 =0.7273 A
したがって、補償定理から計算された電流の変化は、元の回路から計算された電流の変化と同じであることが証明されています。
- 関連記事: ACおよびDC回路の最大電力伝達定理
例-2
以下の回路で、補償定理を使用して3Ω抵抗を7Ω抵抗に置き換えた場合の電流の変化を求めます。そして、補償定理を証明します。
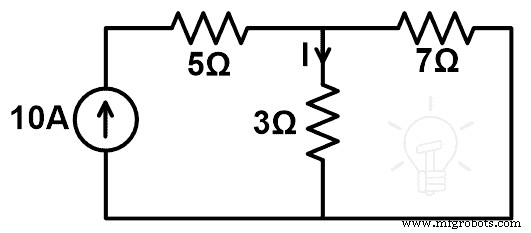
上記のネットワークは、抵抗と独立した電流源のみで構成されています。したがって、このネットワークに補償定理を適用できます。
この図では、ネットワークは現在のソースから供給されています。ここで、3Ωの抵抗分岐を流れる電流を見つける必要があります。この電流は、KCLまたはKVLを使用して見つけることができます。しかし、ここでは、この電流は分流の法則によって簡単に見つけることができます。
したがって、現在の分流の法則に従って;
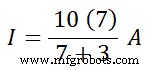
私 =70÷10A
私 =7 A
3Ωの抵抗を備えた元のネットワークでは、その分岐を通過する電流は3Aです。次に、この抵抗を3Ωから7Ωに変更する必要があります。この変更により、そのブランチを通過する電流が変更されます。そして、補償定理によってこの電流の変化を見つけます。
そのためには、補償ネットワークを構築する必要があります。補償ネットワークを作成するには、電圧源を短絡し、電流源を開放することによって、ネットワークで利用可能なすべての独立したソースを削除する必要があります。
このネットワークでは、現在使用できるソースは1つだけです。電流源は理想的な電流源であると想定しています。したがって、内部抵抗を追加する必要はありません。
補償回路で行う必要のある2番目の変更は、追加の電圧源を追加することです。そして、この電圧の値は次のとおりです。
V C =私 ΔZ
V C =7×(7 – 3)
V C =7×4
V C =28 V
報酬ネットワークは次の図のようになります。
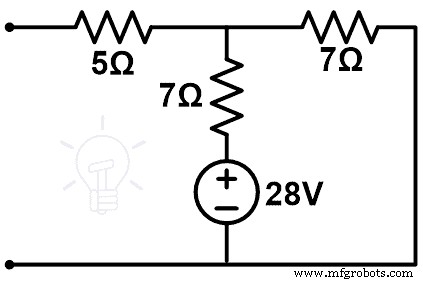
この図にはループが1つだけあります。そして、7Ωの分岐を通過する電流は、電流の変化(ΔI)を与えます。
Δ私 = V C ÷(7 + 7)
Δ私 =28÷14
Δ私 =2 A
補償定理を証明するために、7Ωの抵抗が接続された回路の電流を求めます。変更された回路図を次の図に示します。
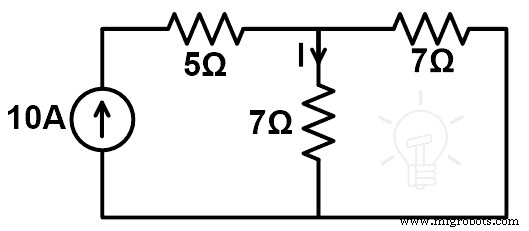
I” =(10(7))÷(7 + 7)
I” =70÷14
I” =5 A
現在の分流の法則を適用することによって;
電流の変化を見つけるには、元のネットワークを通過する電流からこの電流を差し引く必要があります。
Δ私 =私 –私"
Δ私 =7 – 5
Δ私 =2 A
したがって、補償定理を証明しました。
関連する電気回路解析チュートリアル:
- SUPERNODE回路解析–解決例を使用したステップバイステップ
- SUPERMESH回路解析–解決例を使用したステップバイステップ
- キルヒホッフの電流および電圧法(KCLおよびKVL)|解決した例
- クラメルの公式計算機–電気回路用の2および3方程式システム
- 電気電子工学計算機
- 5000以上の電気電子工学の公式と方程式
産業技術



