AC相

互いにずれている2つ以上のAC電圧または電流を関連付ける必要がある場合、事態は複雑になり始めます。 「脱調」とは、2つの波形が同期していないことを意味します。つまり、それらのピークとゼロ点が同じ時点で一致していません。下の図のグラフは、この例を示しています。

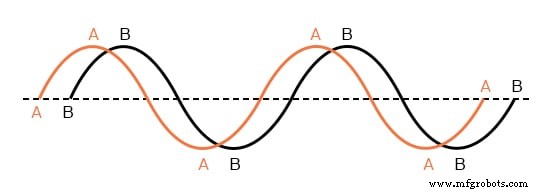
位相がずれた波形。

上に示した2つの波（A対B）は同じ振幅と周波数ですが、互いにずれています。技術用語では、これは位相シフトと呼ばれます 。以前、0〜360度の範囲の角度、完全な円の三角関数の正弦関数を計算することにより、「正弦波」をプロットする方法を説明しました。

正弦波の開始点は、0度で振幅がゼロで、90度で完全な正の振幅に進み、180度でゼロになり、270度で完全に負になり、360度でゼロの開始点に戻りました。

波形プロットの水平軸に沿ったこの角度スケールを使用して、ある波が別の波とどれだけ離れているかを表すことができます。下の図

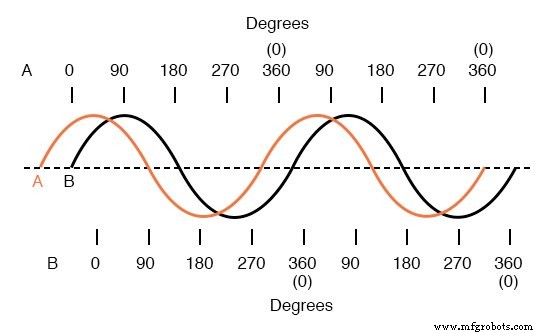
波Aは波Bより45°進んでいます

これら2つの波形間のシフトは約45度で、「A」波が「B」波よりも進んでいます。この概念をよりよく説明するために、さまざまな位相シフトのサンプルを次のグラフに示します。下の図

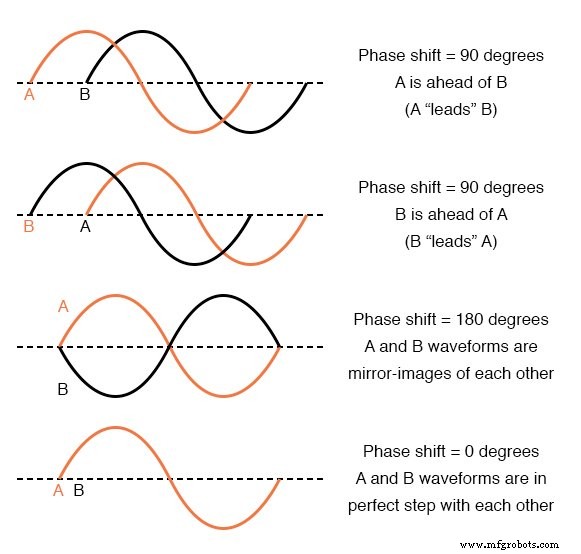
位相シフトの例。

上記の例の波形は同じ周波数であるため、すべての時点で同じ角度量だけずれます。このため、同じ周波数の2つ以上の波形の位相シフトを、波に沿った2つの特定のポイント間のシフトの表現だけでなく、波全体の一定量として表現できます。

つまり、「電圧「A」は電圧「B」と45度位相がずれている」などと言っても差し支えありません。どちらの波形がその進化の先を進んでいるかは、主要なと言われています。 後ろにあるのは遅れていると言われています 。

電圧と同様に、位相シフトは常に2つのものの間の相対的な測定値です。 絶対の波形のようなものは実際にはありません 位相の既知の普遍的な参照がないため、位相測定。

通常、AC回路の分析では、電源の電圧波形が位相の基準として使用され、その電圧は「0度でxxxボルト」と示されます。その回路内の他のAC電圧または電流は、そのソース電圧を基準にして位相シフトが表されます。

これが、AC回路の計算をDCよりも複雑にしている理由です。オームの法則とキルヒホッフの法則を適用する場合、AC電圧と電流の量は、振幅だけでなく位相シフトも反映する必要があります。加算、減算、乗算、除算の数学演算は、振幅だけでなく、これらの量の位相シフトにも作用する必要があります。

幸いなことに、複素数と呼ばれる量の数学的システムがあります。 振幅と位相を表すこのタスクに最適です。

複素数の主題はAC回路を理解するために非常に重要であるため、次の章ではその主題だけに専念します。

レビュー：

• 位相シフト 2つ以上の波形が互いにずれている場所です。
• 2つの波の間の位相シフトの量は、三角関数の正弦関数のプロットに使用される波形グラフの水平軸上の度単位で定義されるように、度で表すことができます。
• 一流 波形は、その進化において別の波形よりも進んでいる1つの波形として定義されます。 遅れ 波形は後ろにあるものです。例：

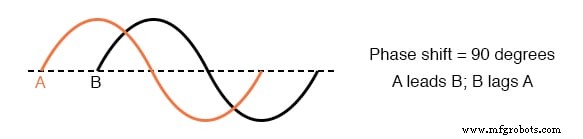
• AC回路解析の計算では、電圧波形と電流波形の振幅と位相シフトの両方を考慮して、完全に正確にする必要があります。これには、複素数と呼ばれる数学システムを使用する必要があります。 。

関連するワークシート：

• AC回路ワークシートの三角法