複素数演算
複素数はスカラー数と同じように正当な数学的実体であるため、他の種類の数と同じように、加算、減算、乗算、除算、二乗、反転などを行うことができます。
関数電卓の中には、2つ以上の複素数に対してこれらの操作を直接実行するようにプログラムされているものもありますが、これらの操作は「手動」で実行することもできます。このセクションでは、基本的な操作がどのように実行されるかを示します。
非常に 複素数に対して簡単に算術関数を実行できる関数電卓を装備することをお勧めします。これにより、すべての計算を長時間行う必要がある場合よりも、AC回路の研究がはるかに快適になります。
長方形形式の複素数の加算と減算
長方形の複素数での足し算と引き算は簡単です。さらに、複素数の実数成分を合計して合計の実数成分を決定し、複素数の虚数成分を合計して合計の虚数成分を決定します。
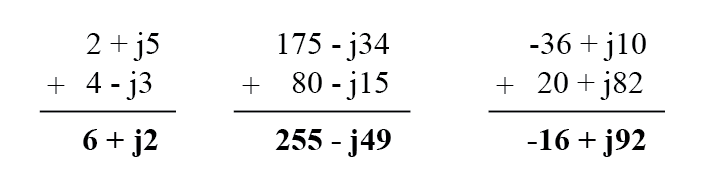
複素数を長方形で減算する場合は、最初の複素数の実数成分から2番目の複素数の実数成分を減算して、差の実数成分に到達し、の虚数成分から2番目の複素数の虚数成分を減算します。違いの架空の要素に最初に到達したもの:
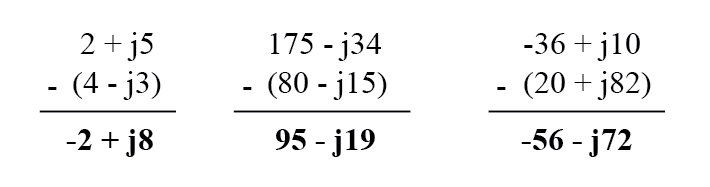
極形式の複素数の乗算と除算
長い乗算と除算の場合、極性は使用するのに適した表記法です。複素数を極形式で乗算する場合は、単に乗算します。 複素数の極の大きさを決定して積の極の大きさを決定し、追加 製品の角度を決定するための複素数の角度:
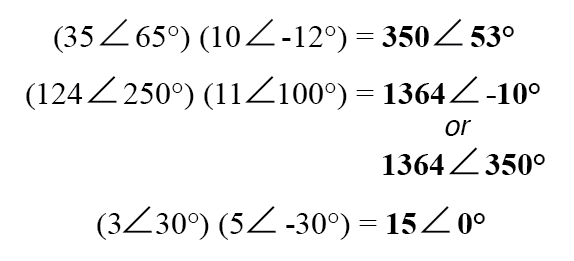
極形式の複素数の除算も簡単です。最初の複素数の極の大きさを2番目の複素数の極の大きさで割って、商の極の大きさに到達し、から2番目の複素数の角度を引くだけです。商の角度に到達する最初の複素数の角度:
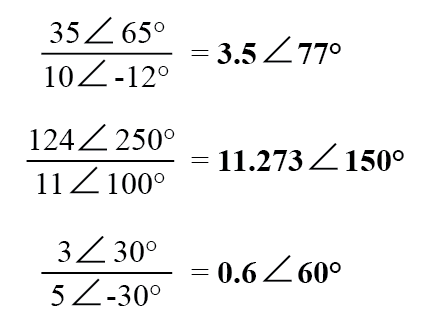
複素数の逆数または「反転」(1 / x)を取得するには、数値(極形式)をスカラー値1に分割します。これは、虚数成分のない複素数にすぎません(角度=0):
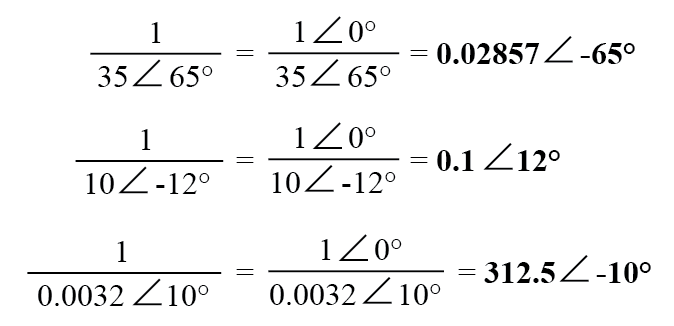
これらは、AC回路の分析で複素数を操作するために知っておく必要のある基本的な操作です。ただし、複素数の演算は、加算、減算、乗算、除算、および反転だけに限定されるわけではありません。
スカラー数で実行できる事実上すべての算術演算は、累乗、根、複素係数を使用した同時方程式の解法、さらには三角関数を含む複素数で実行できます(ただし、これには、双曲線関数と呼ばれる三角関数のまったく新しい視点が含まれます) これは、この説明の範囲をはるかに超えています。
加算、減算、乗算、除算、反転の基本的な算術演算に精通していることを確認してください。AC回路解析にほとんど問題はありません。
レビュー:
- 長方形の形式で複素数を追加するには、実数成分と虚数成分を追加します。減算も同様です。
- 極形式の複素数を乗算するには、大きさを乗算し、角度を加算します。除算するには、大きさを除算し、一方の角度をもう一方の角度から減算します。
関連ワークシート:
- ACフェーズワークシート
産業技術



