数字と記号

数値の表現は当たり前のことです。これは、電子工学の研究において良いことでも悪いことでもあります。

電子回路の分析に使用される多くの計算で数値を使用および操作することに慣れているという点で、これは良いことです。

一方、小学校以降に教えられてきた特定の表記法は ではありません。 最新の電子コンピューティングデバイスで内部的に使用されているシステムであり、さまざまな表記法を学習するには、深く根付いた仮定を再検討する必要があります。

数字

まず、数字と数字を表すために使用する記号の違いを区別する必要があります。 番号 は数学的な量であり、通常、電子機器では電圧、電流、抵抗などの物理量と相関関係があります。数字にはさまざまな種類があります。たとえば、いくつかのタイプを次に示します。

整数：
1、2、3、4、5、6、7、8、9。 。 。

整数：
-4、-3、-2、-1、0、1、2、3、4。 。 。

無理数：
π（約3.1415927）、
e（約2.718281828）、
任意の素数の平方根

実数：
（すべての1次元数値、負および正、
ゼロ、整数、無理数を含む）

複素数：
3-j4、34.5∠20 ^o

さまざまな種類の数字は、現実の世界でさまざまな用途を見つけます。整数は、回路内の抵抗の数など、個別のオブジェクトをカウントするのに適しています。整数の負の等価物が必要な場合は整数が必要です。

無理数は、2つの整数の比率として正確に表現できない数であり、完全な円の円周とその直径（π）の比率は、この良い物理的な例です。 DC回路で処理するのに慣れている非整数の電圧、電流、抵抗は、分数または小数の実数で表すことができます。

ただし、AC回路解析では、実数は大きさと位相角の二重の本質を捉えることができないため、長方形または極形式の複素数の使用に目を向けます。

記号

数字を使用して現実世界のプロセスを理解したり、科学的な予測を行ったり、小切手帳のバランスをとったりする場合は、それらを象徴的に示す方法が必要です。

言い換えれば、当座預金口座にいくらのお金があるかはわかっているかもしれませんが、それを記録するには、紙にその量を象徴するシステム、または記録を保持するための他の種類の形式を作成する必要があります。追跡。

アナログとデジタル

これを行うには、アナログとデジタルの2つの基本的な方法があります。アナログ表現では、量は無限に割り切れる方法で象徴されます。デジタル表現では、数量は個別にパッケージ化された方法でシンボル化されます。

アナログ表現

あなたはおそらくすでにお金のアナログ表現に精通していて、それが何であるかを理解していませんでした。赤い柱の高さが原因のために集められた金額を示している、温度計の写真が描かれた募金ポスターを見たことがありますか？集めたお金が多ければ多いほど、ポスターの赤いインクの柱は高くなります。

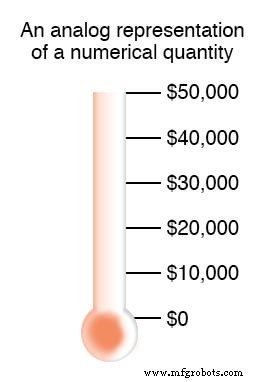
これは、数値のアナログ表現の例です。アカウントの金額を表すために、その列の高さをどれだけ細かく分割できるかについて、実際の制限はありません。その柱の高さを変更することは、それが何であるかという本質的な性質を変えることなく行うことができるものです。

長さは、実際的な制限なしに、必要に応じて分割できる物理量です。計算尺は、まったく同じ物理量（長さ）を使用して数値を表し、一度に2つ以上の数値で算術演算を実行するのに役立つ機械装置です。それもアナログデバイスです。

デジタル表現

一方、デジタル 標準の記号（暗号と呼ばれることもあります）で書かれた同じ金額の表現は、次のようになります。

35,955.38ドル

赤い列のある「温度計」ポスターとは異なり、上記の記号文字を細かく分割することはできません。暗号の特定の組み合わせは、1つの量と1つの量のみを表します。

アカウントにさらにお金が追加された場合（+ $ 40.12）、新しい残高（$ 35,995.50）を表すために異なる記号を使用するか、少なくとも同じ記号を異なるパターンで配置する必要があります。これはデジタル表現の例です。

計算尺（アナログ）に対応するものもデジタルデバイスです。そろばんは、数を象徴するためにロッド上を前後に移動するビーズを備えています。

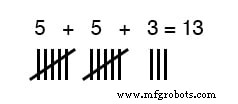
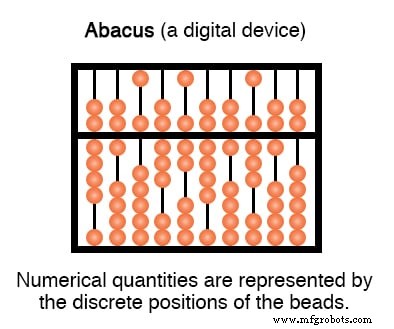
アナログ表現とデジタル表現の対比

数値表現のこれら2つの方法を対比してみましょう：

アナログデジタル
---------------------------------------------- --------------------
直感的に理解-----------解釈するにはトレーニングが必要です
無限に分割可能--- -----------離散
精度のエラーが発生しやすい------絶対精度

数字記号の解釈は、長年教えられてきたため、当たり前のことと思われがちです。しかし、10進数を知らない人に何かの量を伝えようとしても、その人は簡単な体温計チャートを理解することができます！

無限に分割可能な対離散的で正確な比較は、実際には同じコインの裏返しです。デジタル表現が個々の個別の記号（10進数とそろばんビーズ）で構成されているという事実は、必然的に、正確なステップで量を象徴できることを意味します。

一方、アナログ表現（計算尺の長さなど）は、個々のステップではなく、連続した可動域で構成されます。計算尺が数値を無限の解像度に特徴づける能力は、不正確さのトレードオフです。

計算尺がぶつかると、計算尺に「入力」された数値の表現にエラーが発生します。ただし、そろばんは、ビーズがその場所から完全に外れる前に、はるかに強くぶつけなければなりません（別の数を表すのに十分です）。

デジタル表現はアナログよりも必然的に正確であると考えて、この精度の違いを誤解しないでください。時計がデジタルであるからといって、それが常にアナログ時計よりも正確に時刻を読み取ることを意味するわけではありません。それは、解釈を意味するだけです。 表示のあいまいさが少なくなります。

アナログ表現とデジタル表現の分割可能性は、無理数の表現について話すことでさらに明らかになります。 πなどの数値は、整数の分数または整数として正確に表現できないため、無理数と呼ばれます。

過去に分数22/7を計算のπに使用できることを学んだかもしれませんが、これは単なる近似値です。実際の数「円周率」は、有限または制限された小数点以下の桁数で正確に表すことはできません。円周率の桁は永遠に続きます：

3.1415926535897932384。 。 。 。 。

アナログ記号には増減できる程度の最小制限がないため、少なくとも理論的には、計算尺（または温度計の列）を計算尺（または温度計の列）を設定して、数πを完全に表すことができます。

>

計算尺が3.141592654ではなく3.141593の数字を示している場合は、スライドをもう少し（または少なく）バンプして、さらに近づけることができます。ただし、そろばんなどのデジタル表現では、πをさらに正確に表現するために追加のロッド（プレースホルダーまたは数字）が必要になります。

10本の棒のそろばんは、ビーズをどのようにセットしても、10桁以上の数πを表すことはできません。 πを完全に表現するには、そろばんには無限の数のビーズとロッドが必要です。もちろん、トレードオフは、アナログ記号の調整と読み取りに対する実際的な制限です。

実際には、計算尺の目盛りは粗すぎて人間の視覚が制限されているため、計算尺の目盛りを10桁の精度で読み取ることはできません。一方、そろばんは、解釈エラーなしで設定および読み取りが可能です。

さらに、アナログ記号には、正確な解釈のために比較できるある種の標準が必要です。計算尺には、長さを標準的な量に変換するために、スライドの長さに沿って印刷されたマーキングがあります。

体温計のチャートでさえ、高さに沿って数字が書かれており、特定の高さに対して赤い列が表す金額（ドル）を示しています。さまざまな距離で手を離して、単純な数字を互いに伝えようとした場合を想像してみてください。

数字の1は、手を1インチ離して、数字の2を2インチ離して、というように表すことができます。誰かが17インチ離れて数字を表すために手を握った場合、周囲の誰もがその距離を17として即座に正確に解釈できるでしょうか。おそらくそうではありません。

短いと推測する人もいれば（15または16）、長いと推測する人もいます（18または19）。もちろん、漁獲量を自慢する漁師は、量の過大評価を気にしません！

おそらくこれが、人々が一般的に数字、特に整数や整数を表すためのデジタル記号に落ち着いた理由です。これらは日常生活で最も多くの用途があります。

手の指を使って、0から10までの整数を記号化する準備ができています。紙、木、石にハッシュマークを付けて、同じ量を非常に簡単に表すことができます。

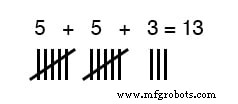
ただし、多数の場合、「ハッシュマーク」の記数法は非効率的です。