複素数の極形式と長方形形式の表記

ベクトルを描画せずに複素数を処理するには、最初にある種の標準的な数学表記が必要です。複素数表記には、次の2つの基本的な形式があります。極 および長方形 。

複素数の極形式

極形式では、複素数は長さで表されます。 （別名マグニチュード 、絶対値 、またはモジュラス ）と角度 そのベクトルの（通常は次のような角度記号で示されます：∠）。

マップの例えを使用すると、ニューヨーク市からサンディエゴまでのベクトルの極座標表記は、「南西2400マイル」のようになります。ベクトルとその極性表記の2つの例を次に示します。

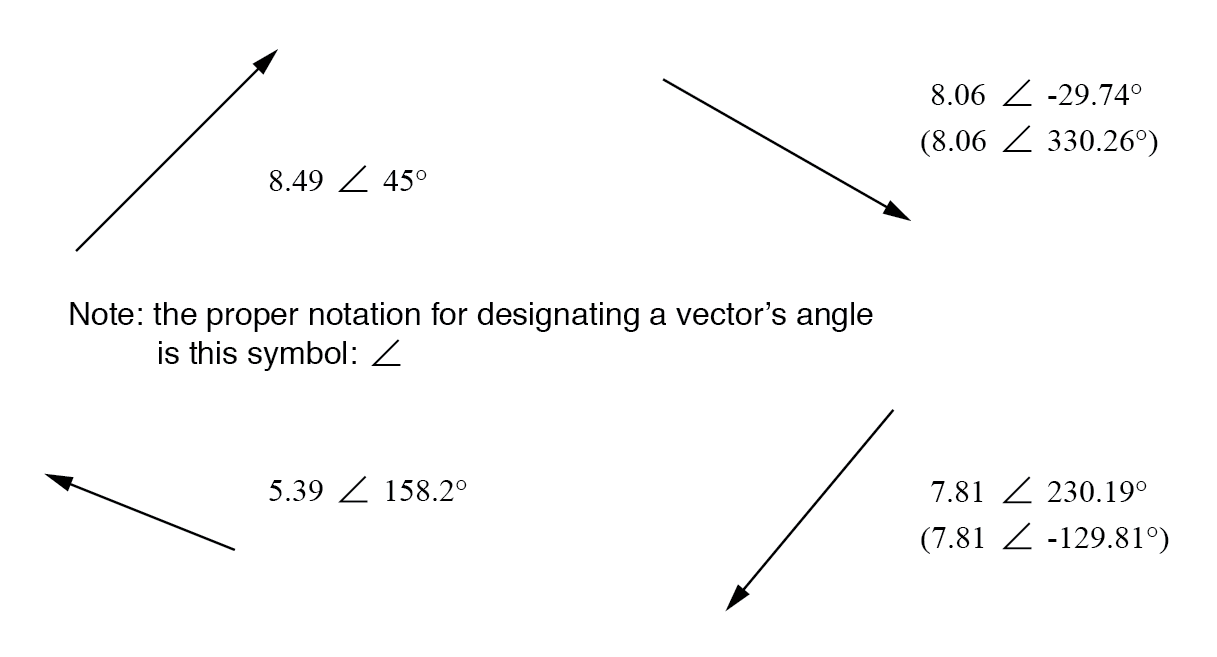
極性表記のベクトル。

AC回路計算でのベクトル角度の標準的な向きは、0°を右（水平）であると定義し、90°を真上に、180°を左に、270°を真下に向けます。 「下向き」の角度のベクトルは、180を超える正の数、または180未満の負の数として極形式で表される角度を持つ可能性があることに注意してください。

たとえば、∠270°（真っ直ぐ下）の角度のベクトルは、-90°の角度を持っているとも言えます。 （下の図）上記の右側のベクトル（7.81∠230.19°）は、7.81∠-129.81°と表すこともできます。

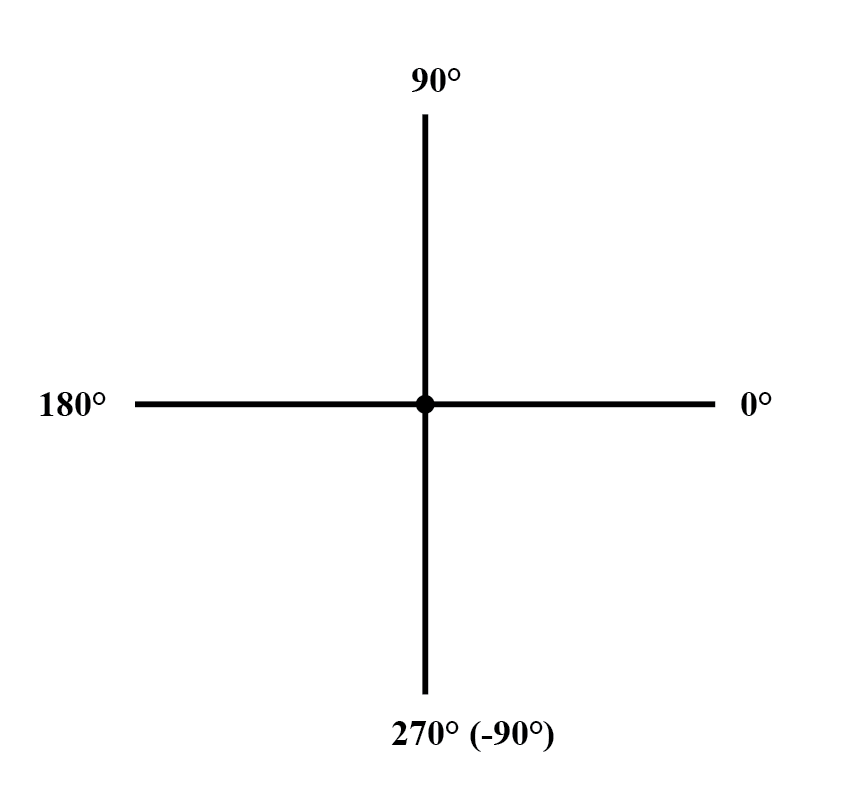
ベクトルコンパス。

複素数の長方形

一方、長方形の形式では、複素数はそれぞれの水平成分と垂直成分で表されます。本質的に、角度の付いたベクトルは、隣接する辺と反対側の辺の長さで表される直角三角形の斜辺と見なされます。

ベクトルの長さと方向を大きさと角度で表すのではなく、「左/右の距離」と「上下の距離」で表します。

これらの2次元の図形（水平および垂直）は、2つの数字で表されます。水平方向と垂直方向の寸法を互いに区別するために、垂直方向には小文字の「i」（純粋数学の場合）または「j」（電子機器の場合）が接頭辞として付けられます。

これらの小文字は、物理変数（瞬時電流など、小文字の「i」で表される）を表すのではなく、数学的な演算子です。 ベクトルの垂直成分と水平成分を区別するために使用されます。完全な複素数として、水平方向と垂直方向の量は合計として書き込まれます:(下の図）

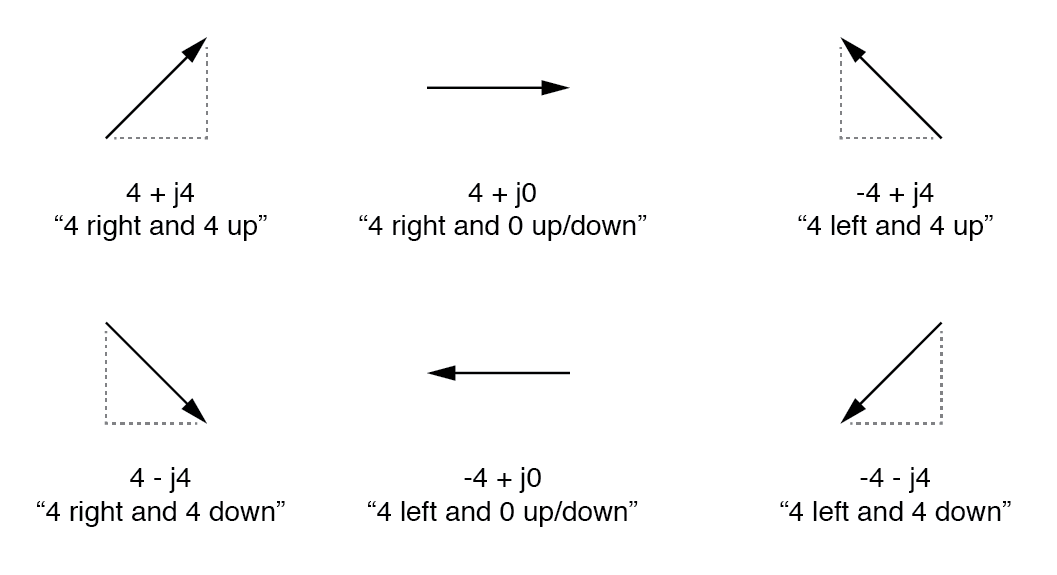
「長方形」の形式では、ベクトルの長さと方向は水平方向と垂直方向のスパンで表され、最初の数字は水平（「実数」）を表し、2番目の数字は水平（「実数」）を表します。垂直（「架空」）の寸法を表す数値（「j」の接頭辞付き）。

水平成分はレアルと呼ばれます その次元は通常のスカラー（「実数」）数と互換性があるため、コンポーネント。垂直成分は架空と呼ばれます その次元は別の方向にあり、実数のスケールとは完全に異質であるため、コンポーネント。 （下の図）

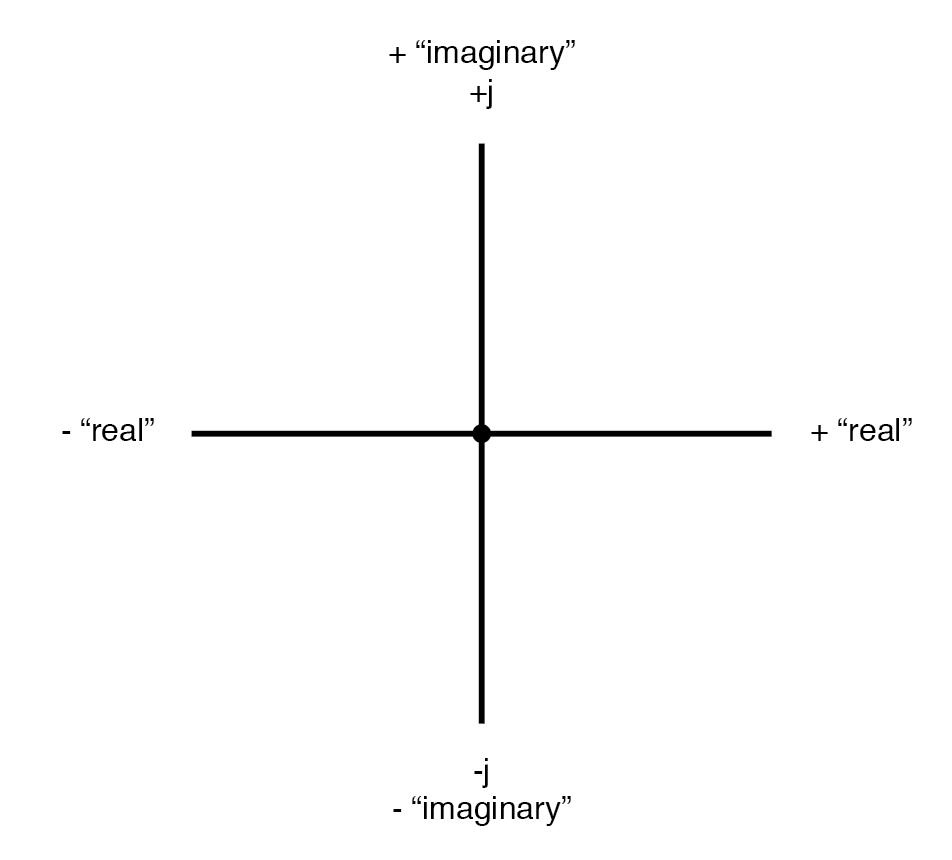
実軸と虚軸を示すベクトルコンパス。

グラフの「実際の」軸は、前に見たおなじみの数直線に対応しています。正と負の両方の値が付いているものです。グラフの「虚数」軸は、「実数直線」に対して90°の位置にある別の数直線に対応しています。

ベクトルは2次元のものであるため、ベクトルを表現するための2次元の「マップ」が必要です。したがって、2本の数直線は互いに垂直です:(下の図）

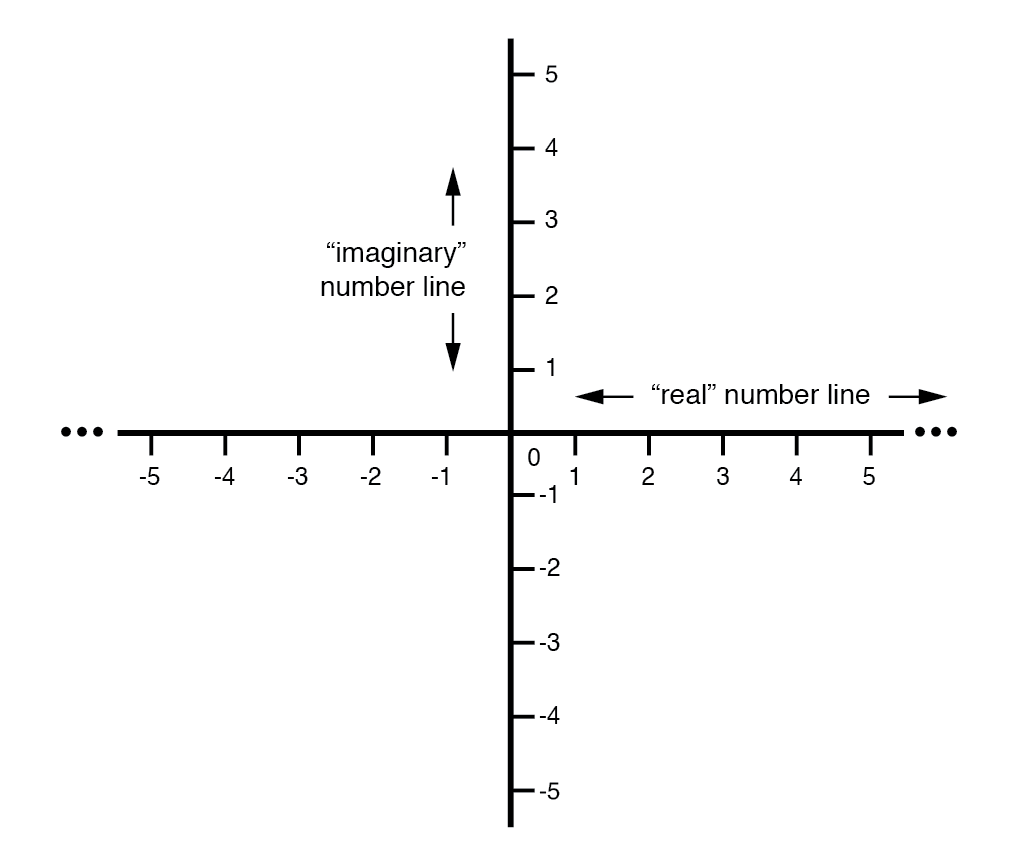
実数直線と虚数直線（ "j"）のベクトルコンパス。

極形式から長方形形式への変換

どちらの表記方法も複素数に有効です。 2つの表記方法がある主な理由は、長い計算を簡単にするためです。長方形の形式は加算と減算に役立ち、極形式は乗算と除算に役立ちます。

2つの表記形式間の変換には、単純な三角法が含まれます。極座標から直交座標に変換するには、極座標の大きさに角度の正弦を掛けて実数成分を見つけ、極座標の大きさに角度の正弦を掛けて虚数成分を求めます。

これは、直角三角形の辺として量を描くことでより簡単に理解できます。三角形のハイポテヌスはベクトル自体（極形を構成する水平に対する長さと角度）を表し、水平と垂直の辺は「それぞれ「実数」および「虚数」の長方形コンポーネント:(下の図）

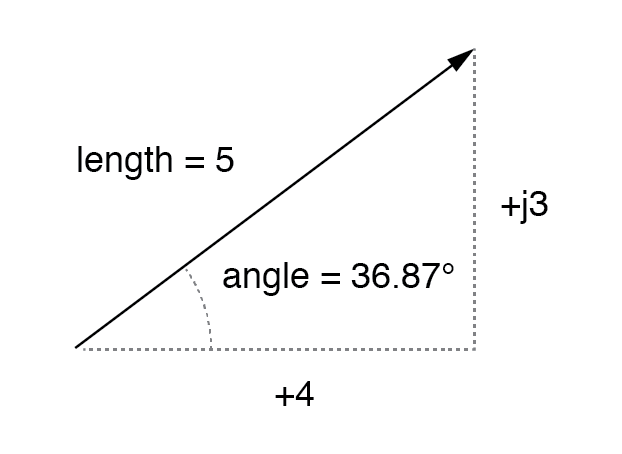
実数（4）および虚数（j3）の成分に関する大きさのベクトル。

長方形形式から極形式への変換

直交から極に変換するには、ピタゴラスの定理を使用して極の大きさを求めます（極の大きさは直角三角形の斜辺であり、実数成分と虚数成分はそれぞれ隣接する辺と反対側です）。虚数成分の弧を実数成分で割ったものを取ります：

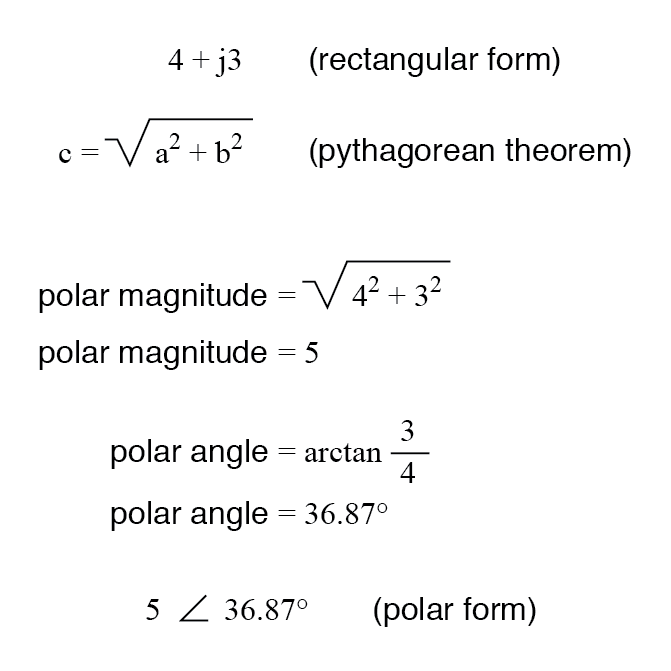
レビュー：

• ポーラー 表記は、ベクトルの長さと開始点からの角度方向に関する複素数を示します。例：45マイル∠203°（西から南西）を飛行します。
• 長方形 表記は、水平方向と垂直方向の寸法に関して複素数を示します。例：西に41マイル運転し、次に曲がって南に18マイル運転します。
• 長方形表記では、最初の量は「実数」成分（ベクトルの水平方向の次元）であり、2番目の量は「虚数」成分（ベクトルの垂直方向の次元）です。虚数成分の前には小文字の「j」が付いており、 j演算子と呼ばれることもあります。 。
• 複素数の表記の極形式と長方形形式の両方を直角三角形の形式でグラフィカルに関連付けることができます。斜辺はベクトル自体を表します（極形式：斜辺の長さ=大きさ、水平辺に対する角度=角度） ）、水平側は長方形の「実」コンポーネントを表し、垂直側は長方形の「仮想」コンポーネントを表します。

関連ワークシート：

• ACフェーズワークシート