ノートンの定理。例を使用した簡単なステップバイステップの手順

DC回路解析におけるノートンの定理

ノートンの定理は、テブナンの定理を使用するなど、電気回路を分析するためのもう1つの便利な手法です。これにより、線形のアクティブな回路や複雑なネットワークが単純な等価回路になります。テブナンの定理とノートンの定理の主な違い つまり、テブナンの定理は等価電圧源と等価直列抵抗を提供し、ノートンの定理は等価電流源と等価並列抵抗を提供します。

ノートンの定理 述べている：

簡単に言うと、線形回路は特定の端子の実際の独立した電流源に相当します。

関連記事：テブナンの定理。例を使用した簡単なステップバイステップの手順（図解）

ノートンの定理を使用して電気回路を分析する手順

1. 負荷抵抗を短くします。
2. 短絡電流を計算/測定します。これはノートン電流（I _N 。
3. オープン電流源、ショート電圧源、およびオープン負荷抵抗。
4. 開回路抵抗を計算/測定します。これはノートン抵抗（R _N 。
5. ここで、測定された短絡電流（I _N ）を使用して回路を再描画します。 ）ステップ（2）で電流源として測定された開回路抵抗（R _N ）手順（4）で並列抵抗として接続し、手順（3）で取り外した負荷抵抗を接続します。これは、その線形電気ネットワークまたは複雑な回路の同等のノートン回路であり、単純化して分析する必要がありました。完了しました。
6. ここで、分流の法則を使用して、負荷抵抗を流れる負荷電流と負荷抵抗の両端の負荷電圧を見つけます。 I _L =I _N /（R _N /（R _N + R _L ）） （（明確な説明については…以下の解決された例を確認してください。）

解決された例 ノートンの 定理：

例：

R _Nを検索 、I _N 、ノートンの定理を使用して、図（1）の負荷抵抗に流れる電流と負荷電圧。

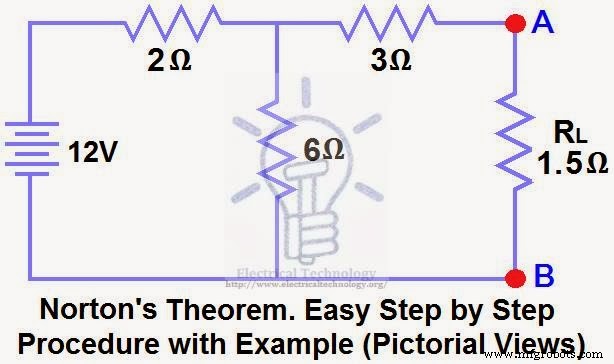
解決策：-

ステップ1。

（図2）に示すように、1.5Ωの負荷抵抗を短くします。

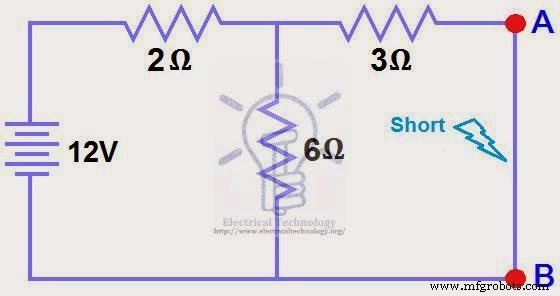
ステップ 2.

短絡電流を計算/測定します。これはノートン電流（I _N 。

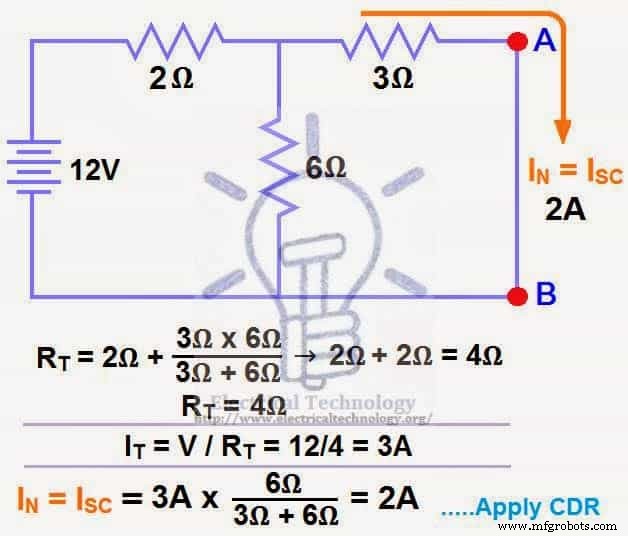
ノートン電流I_{Nを決定するためにAB端子を短絡しました。} 次に、6Ωと3Ωが並列になり、6Ωと3Ωのこの並列の組み合わせが2Ωと直列になります。

したがって、ソースに対する回路の合計抵抗は次のようになります。-

2Ω+（6Ω||3Ω）…..（|| =並列）

R _T =2Ω+[（3Ωx6Ω）/（3Ω+6Ω）]→I _T =2Ω+2Ω=4Ω。

R _T =4Ω

I _T =V÷R_T

I _T =12V÷4Ω

I _T =3A ..

ここで、I _SCを見つける必要があります。 =I _N …CDRを適用する…（現在の分流の法則）…

I _SC =I _N =3A x [（6Ω÷（3Ω+6Ω）]=2A。

I _SC =I _N =2A。

ステップ 3.

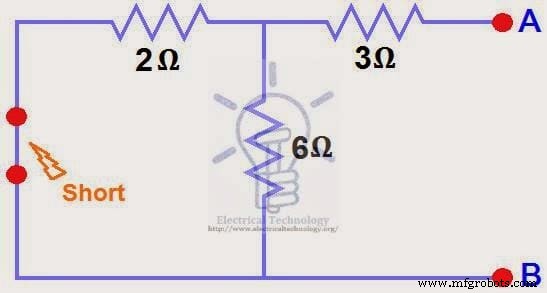
オープン電流源、ショート電圧源、およびオープン負荷抵抗。図（4）

ステップ 4.

開回路抵抗を計算/測定します。これはノートン抵抗（R _N ）

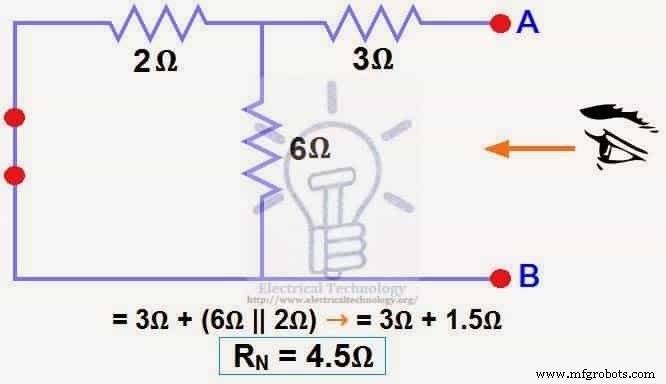
12V DCソースをゼロに減らしました。これは、図（4）に示すように、ステップ（3）でショートに置き換えるのと同じです。3Ωの抵抗が6Ω抵抗と2Ω抵抗の並列組み合わせと直列に接続します。つまり：

3Ω+（6Ω||2Ω）…..（|| =並列）

R _N =3Ω+[（6Ωx2Ω）÷（6Ω+2Ω）]

R _N =3Ω+1.5Ω

R _N =4.5Ω

ステップ 5.

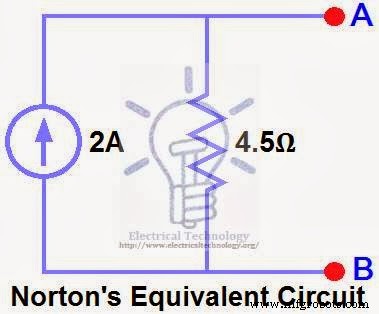
R _Nを接続します 電流源と並行してI_N 負荷抵抗を再接続します。これを図（6）に示します。つまり、負荷抵抗を備えたノートン等価回路です。

ステップ 6.

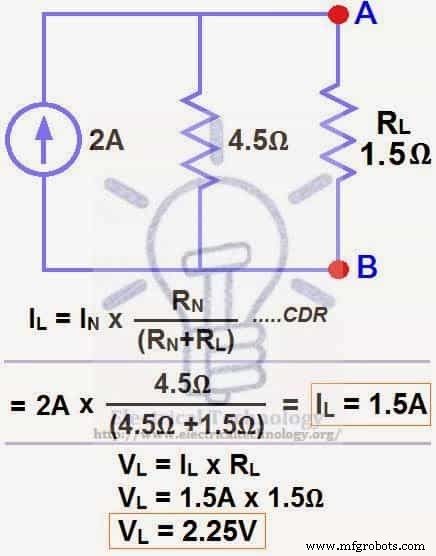
最後のステップを適用します。つまり、図7に示すように、オームの法則に従って、負荷抵抗を流れる負荷電流と負荷抵抗の負荷電圧を計算します。

負荷抵抗を流れる負荷電流…

I _L =I _N x [R _N ÷（R _N + R _L ）]

=2A x（4.5Ω÷4.5Ω+1.5Ω）→=1.5A

I _L =1.5A

そして

負荷抵抗の両端の負荷電圧…

V _L =I _L x R _L

V _L =1.5Ax1.5Ω

V _L =2.25V

次に、この単純な回路を、指定された元の回路と比較します。図1で、ノートンの定理を介して、はるかに複雑な回路でも、さまざまな負荷抵抗の負荷電流と負荷電圧を測定/計算することがどれほど簡単になるかを理解できますか？唯一そしてそうです。

知っておきたいこと： ノートンとテブナンの両方の定理は、抵抗、インダクタ、コンデンサなどの異なるコンポーネントを含むAC回路とDC回路の両方に適用できます。ノートンの電流「I _N AC回路の」は複素数（極形式）で表されますが、ノートンの抵抗「R _N 」は長方形で表されます。

関連記事：

• ACおよびDC回路の最大電力伝達定理
• キルヒホッフの電流および電圧法（KCLおよびKVL）|解決した例
• 補償定理–証明、説明、および解決された例
• 置換定理–解決された例を使用したステップバイステップガイド
• ミルマンの定理– ACおよびDC回路の分析–例
• 重ね合わせの原理–解決例を用いた回路解析
• テレゲンの定理–解決された例とMATLABシミュレーション
• SUPERNODE回路解析|解決された例を使用したステップバイステップ
• SUPERMESH回路解析|解決された例を使用したステップバイステップ
• 分圧器ルール（VDR）– R、L、C回路の解決例
• 現在の分流の法則（CDR）–ACおよびDC回路の解決例
スターからデルタおよびデルタからスターへの変換。 Y-Δ変換