テブナンの定理。解決された例を使用したステップバイステップの手順

DC回路解析におけるテブナンの定理

フランスのエンジニア、M.Lテブナン 、1893年にこれらの飛躍的な進歩の1つを成し遂げました。テブナンの定理 （ヘルムホルツ-テブナンの定理とも呼ばれます ）それ自体は分析ツールではありませんが、アクティブな回路や複雑なネットワークを簡素化する非常に便利な方法の基礎となります。この定理は、複雑な線形回路やネットワーク、特に電気回路や電子ネットワークをすばやく簡単に解くのに役立ちます。

テブナンの定理 以下に記載される場合があります：

• V _TH =テブナンの定理
• R _TH =テブナンの 抵抗

関連記事：ノートンの定理。例を使用した簡単なステップバイステップの手順（図解）

テブナンの定理を使用して電気回路を分析する手順

1. 負荷抵抗を開きます。
2. 開回路電圧を計算/測定します。これはテブナン電圧（V _TH ） 。
3. オープン電流源とショート電圧源。
4. 開回路抵抗を計算/測定します。これはテブナン抵抗（R _TH ） 。
5. 次に、測定された開回路電圧（V _TH ）を使用して回路を再描画します。 ） ステップ（2）で電圧源として測定され、開回路抵抗（R _TH > ） 手順（4）で直列抵抗として接続し、手順（1）で取り外した負荷抵抗を接続します。これは同等のテブナン回路です その線形電気ネットワークの または複雑な回路 テブナンの定理によって簡略化および分析する必要がありました 。あなたはそれをしました。
6. オームの法則を使用して、負荷抵抗を流れる総電流を求めます。 I _T =V _TH /（R _TH + R _L 。
   

関連記事：SUPERMESH回路解析|解決された例を使用したステップバイステップ

テブナンの定理による解決例：

例：

V_THを検索 、R _TH および負荷電流I _L テブナンの定理を使用して、図（1）の負荷抵抗を流れる負荷電圧 。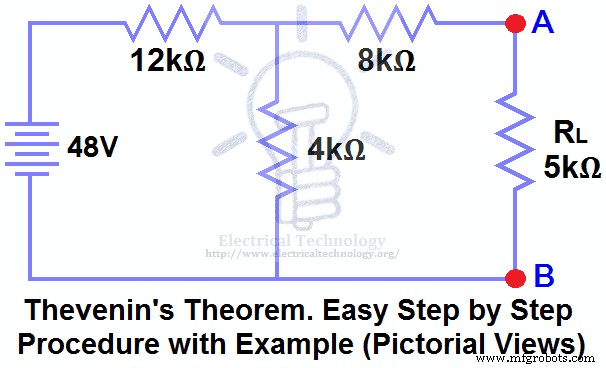

解決策：-

ステップ 1.

5kΩ負荷抵抗を開きます （図2）。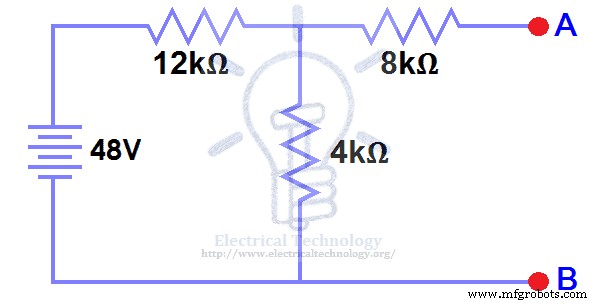

ステップ 2.

開回路電圧を計算/測定します。これはテブナン電圧（V _TH ） 。図（3）。

図1ではすでに負荷抵抗を取り外しているため、回路は開回路になりました。 図2に示すように、テブナンの電圧を計算する必要があります。 3mA以降 電流は両方の12kΩに流れます および4kΩ 抵抗器 これは直列回路であり、電流は8kΩに流れないため 開いたままの抵抗器。

このように、 12V （3mAx4kΩ） 4kΩ抵抗の両端に表示されます 。また、8kΩ抵抗は開回路であるため電流が流れていないこともわかっていますが、8kΩ抵抗は4k抵抗と並列になっています。 。したがって、同じ電圧、つまり12Vが8kΩ抵抗の両端に現れます 同様に4kΩ抵抗。したがって、AB端子間に12Vが現れます。つまり、

V _TH =12V

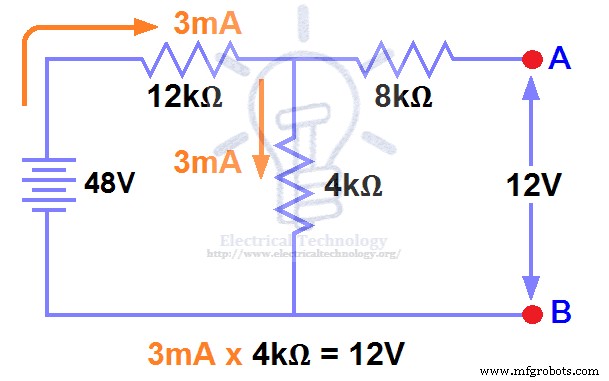
ステップ 3.

現在のソースを開く および短い電圧源 以下に示すように。図（4）

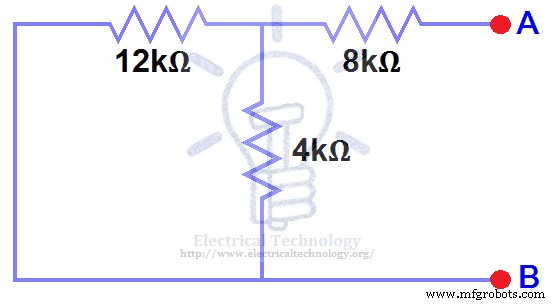
ステップ 4.

計算/開回路抵抗の測定 。これがテブナン耐性（R _TH ）

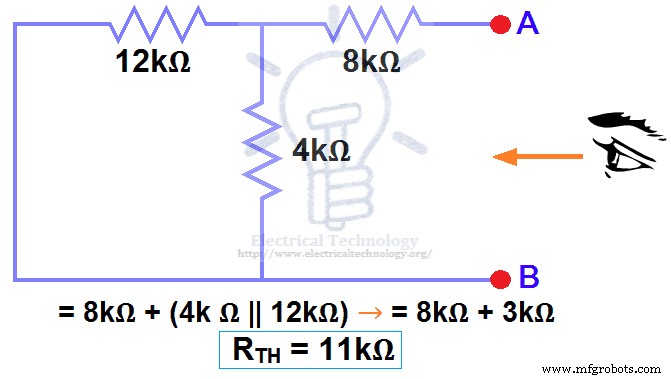
48VDCソースを削除しました ゼロ 同等のものとして、つまり、48V DC電源はステップ3で短絡に置き換えられました（図3を参照）。 8kΩの抵抗が4kΩの抵抗と12kΩの抵抗の並列接続と直列に接続されていることがわかります。つまり：

8kΩ+（4kΩ||12kΩ）…..（|| =並列）

R _TH =8kΩ+[（4kΩx12kΩ）/（4kΩ+12kΩ）]

R _TH =8kΩ+3kΩ

R _TH =11kΩ

ステップ 5.

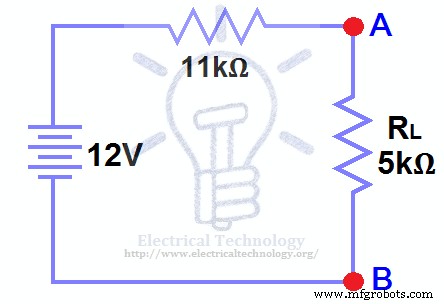
R_THを接続 電圧源V_THと直列 負荷抵抗を再接続します。これを図（6）に示します。つまり、負荷抵抗を備えたテブナン回路です。これはテブナンの等価回路 。

ステップ> 6.

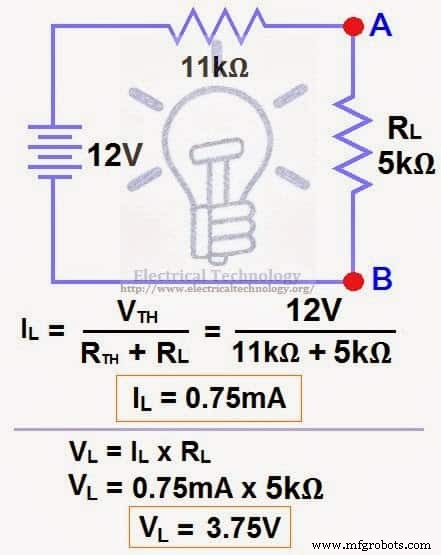
最後のステップ、つまりオームの法則を適用します。 総負荷電流と負荷電圧を計算します 図6に示すように。

I _L =V _TH /（R _TH + R _L ）

I _L =12V /（11kΩ+5kΩ）→=12/16kΩ

I _L =0.75mA

そして

V _L =I _L x R _L

V _L =0.75mAx5kΩ

V _L =3.75V

次に、この単純な回路を図1に示す元の回路と比較します。複雑な回路とネットワークの負荷電流の測定と計算がどれほど簡単になるかわかりますか。 テブナンの定理による負荷抵抗 ？はい、はいのみ。

知っておきたいこと： テブナンの定理とノートンの定理はどちらも、抵抗、インダクタ、コンデンサなどの異なるコンポーネントを含むAC回路とDC回路の両方に適用できます。テブナンの電圧「V _TH」に注意してください。 AC回路の」は複素数（極形式）で表されますが、テブナンの抵抗「R _TH 」は長方形で表されます。

関連記事：

• ACおよびDC回路の最大電力伝達定理
• キルヒホッフの電流および電圧法（KCLおよびKVL）|解決した例
• 補償定理–証明、説明、および解決された例
• 置換定理–解決された例を使用したステップバイステップガイド
• ミルマンの定理– ACおよびDC回路の分析–例
• 重ね合わせの原理–解決例を用いた回路解析
• テレゲンの定理–解決された例とMATLABシミュレーション
• SUPERNODE回路解析|解決された例を使用したステップバイステップ
• SUPERMESH回路解析|解決された例を使用したステップバイステップ
• 分圧器ルール（VDR）– R、L、C回路の解決例
• 現在の分流の法則（CDR）–ACおよびDC回路の解決例
スターからデルタおよびデルタからスターへの変換。 Y-Δ変換