ノートンの定理

ノートンの定理とは何ですか？

ノートンの定理は、どんなに複雑な線形回路でも、単一の電流源と負荷に接続された並列抵抗を備えた等価回路に単純化することが可能であると述べています。テブナンの定理と同様に、「線形」の資格は重ね合わせの定理に見られるものと同じです。基礎となるすべての方程式は線形でなければなりません（指数や根はありません）。

線形回路の簡素化

ノートンの同等の回路と元の回路例を比較すると、次のようになります。

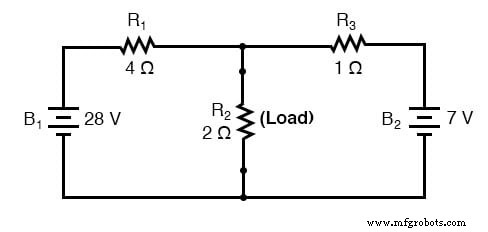
。 。 。ノートン変換後。 。 。

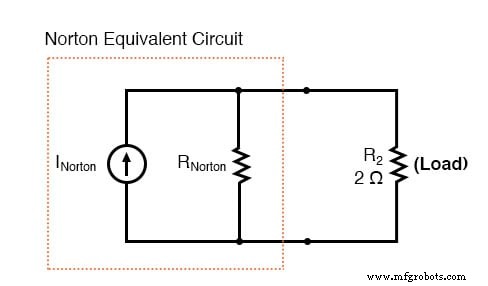
現在のソースを覚えておいてください は、一定量の電流を供給し、その定電流を維持するために必要な電圧を出力することを目的としたコンポーネントです。

テブナンの定理とノートンの定理

テブナンの定理と同様に、負荷抵抗を除く元の回路のすべてが、分析がより簡単な等価回路に削減されました。また、テブナンの定理と同様に、ノートンの定理でノートンのソース電流を計算するために使用される手順があります（I _ノートン ）およびノー​​トン抵抗（R _ノートン 。

負荷抵抗を特定する

前と同じように、最初のステップは負荷抵抗を特定し、それを元の回路から削除することです。

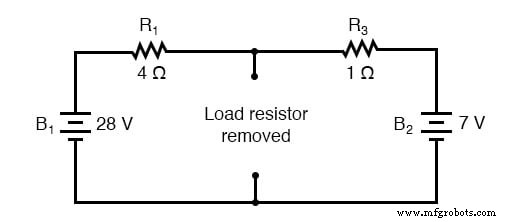
ノートンの定理を見つける

次に、ノートン電流（ノートン等価回路の電流源の場合）を見つけるために、負荷ポイント間に直接ワイヤ（短絡）接続を配置し、結果として生じる電流を決定します。このステップは、負荷抵抗をブレーク（開回路）に置き換えたテブナンの定理のそれぞれのステップとは正反対であることに注意してください。

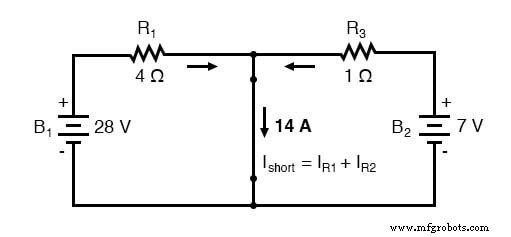
負荷抵抗の接続ポイント間で電圧降下がゼロの場合、R ₁ を流れる電流 厳密にはB1の電圧とR ₁ の関数です の抵抗：7アンペア（I =E / R）。同様に、R ₃ を流れる電流 厳密にはB ₂ の関数になりました の電圧とR ₃ の抵抗：7アンペア（I =E / R）。負荷接続ポイント間の短絡を流れる合計電流は、これら2つの電流の合計です：7アンペア+7アンペア=14アンペア。この14アンペアの数字は、ノートンのソース電流（I _ノートン）になります。 ）等価回路内：

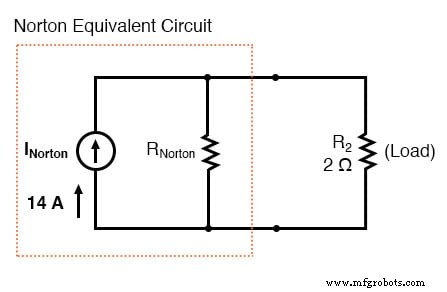
ノートンの抵抗を見つける

電流源の矢印表記は、従来の電流の流れの方向を指していることを忘れないでください。 ノートン抵抗を計算するには（R _ノートン ）、テブナン抵抗を計算するために行ったのとまったく同じことを行います（R _Thevenin ）：元の回路（負荷抵抗を取り外したまま）を取り、電源を取り外し（重ね合わせの原理で行ったのと同じスタイル：電圧源をワイヤーに置き換え、電流源をブレークに置き換え）、一方の負荷接続ポイントからもう一方へ：

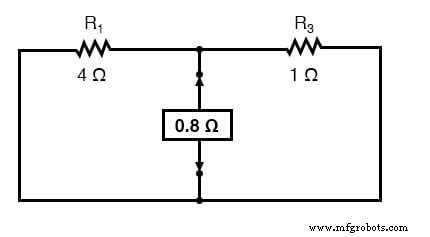
これで、ノートンの等価回路は次のようになります。

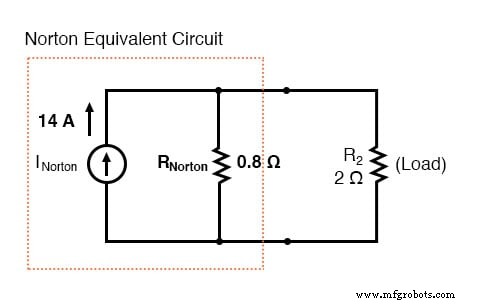
負荷抵抗の両端の電圧を決定する

2Ωの元の負荷抵抗を再接続すると、ノートン回路を単純な並列配置として分析できます。

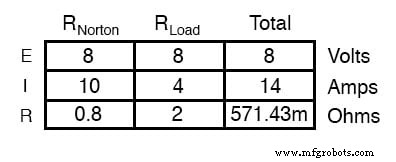
テブナン等価回路と同様に、この分析から得られる唯一の有用な情報は、R ₂ の電圧と電流の値です。;残りの情報は、元の回路とは無関係です。ただし、テブナンの定理で見られるのと同じ利点がノートンの定理にも当てはまります。負荷抵抗のいくつかの異なる値で負荷抵抗の電圧と電流を分析する場合は、ノートンの等価回路を何度も使用できます。各試行負荷で何が起こっているかを判断するための単純な並列回路分析。

レビュー：

• ノートンの定理は、ネットワークを、単一の電流源、並列抵抗、および並列負荷で構成される等価回路に縮小する方法です。
• ノートンの定理に従うための手順：
  • 元の回路から負荷抵抗を削除し、負荷抵抗があった開いている接続ポイントを飛び越える短い（ワイヤ）を流れる電流を計算して、ノートンのソース電流を見つけます。
  • 元の回路のすべての電源を削除し（電圧源が短絡し、電流源が開いている）、開いている接続ポイント間の合計抵抗を計算して、ノートンの抵抗を見つけます。
  • ノートンの電流源をノートンの抵抗と並列にして、ノートンの等価回路を描きます。負荷抵抗は、等価回路の2つのオープンポイントの間に再接続します。
  • 並列回路の規則に従って、負荷抵抗の電圧と電流を分析します。

関連ワークシート：

• テブナン、ノートン、および最大電力伝達定理ワークシート