キルヒホッフの電流および電圧法(KCLおよびKVL)|解決した例
KCL&KVL –キルヒホッフの第1法則と第2法則と解決例
ドイツの物理学者「ロバートキルヒホフ」は、1847年に2つの重要な電気法則を導入しました。これにより、複雑なネットワークの等価抵抗とさまざまな導体の電流を簡単に見つけることができます。キルヒホッフの電流法則(KCL)およびキルヒホッフの電圧法則(KVL)として知られているこれらの単純な法則を使用することにより、AC回路とDC回路の両方を解決および簡略化できます。
また、KCLは電磁気学の電荷連続方程式から導出され、KVLは静磁場のマクスウェル-ファラデー方程式から導出されることに注意してください(時間に関するBの導関数は0です)。 。
キルヒホッフの現行法(KCL):
KCLによると:
どの電気ネットワークでも、あるポイントへの入力電流とそのポイントからの出力電流の代数和はゼロです。または、あるポイントへの流入電流は、そのポイントの離脱電流と同じです。
言い換えると、あるポイントに向かって流れる電流の合計は、あるポイントから離れて流れる電流の合計に等しくなります。または、ノードに入る電流の代数和は、ノードから出る電流の代数和に等しくなります。
KCLの説明:
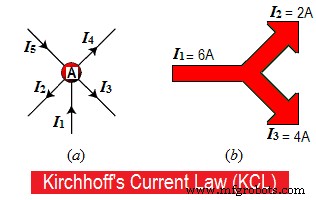
図1.aに示すように、いくつかの指揮者がポイント「A」で合流しているとします。一部の導体では、電流は点「A」に流入しますが、他の導体では、電流は点「A」から流出または流出します。
ポイント「A」からの流出または流出電流が「負(-)」であるのに対し、流入または流入電流は「ポイント「A」に向かって正(+)」と見なします。
次に:
私 1 +(–私 2 )+(–私 3 )+(–私 4 )+私 5 =0
または
私 1 +私 5 –私 2 –私 3 –私 4 =0
または
私 1 +私 5 =私 2 +私 3 +私 4 =0
つまり
電流の入力または入力=電流の出力または出力
または
Σ私 入力=ΣI 離れる
たとえば、図1.bでは、8Aがポイントに近づき、5Aと3Aがそのポイントを離れます。
8A =5A + 3A
8A=8A。
キルヒホッフの電圧法則(KVL):
キルヒホッフの第二法則またはKVLは次のように述べています;
つまり、閉ループ(メッシュとも呼ばれます)では、適用されるEMFの代数和は、要素の電圧降下の代数和に等しくなります。 。キルヒホッフの第2法則は、電圧法則またはメッシュ法則とも呼ばれます。
ΣIR=ΣE
KVLの説明:
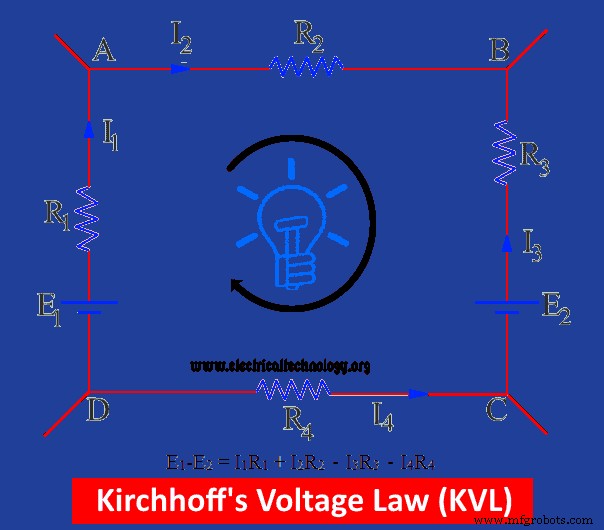
図に、バッテリーE 1の2つの接続を含む閉回路を示します。 およびE2 。バッテリーのE.M.Fの全体の合計は、E 1で示されます。 -E 2 。電流の想像上の方向も図に示されています。
E 1 E 2 の間、正と思われる方向に電流を駆動します 電流の方向に干渉する(つまり、想定される電流の方向と反対の方向にある)ため、負の値と見なされます。この閉回路での電圧降下は、電圧と電流の積に依存します。
想定される電流の方向で発生する電圧降下は正の電圧降下と呼ばれ、もう1つは負の電圧降下です。
上の図では、I 1 R 1 およびI2 R 2 は正の電圧降下であり、I 3 R 3 およびI4 R 4 負のV.D.
閉回路(または各メッシュ)を回って、導体の抵抗とその中を流れる電流を乗算すると、IRの合計は回路に接続されている適用されたEMFソースの合計。
上記の回路の全体的な式は次のとおりです。
E 1 – e 2 = i 1 R 1 + i 2 R 2 – i 3 R 3 – i 4 R 4
図に示すように電流の想定方向に進むと、IRの積は正と見なされ、それ以外の場合は負と見なされます。
知っておきたいこと:
現在の方向:
キルヒホッフの法則を介して回路を解くときは常に、電流の方向を決定することが非常に重要です。選挙の流れと従来の流れの場合と同じです。
電流の方向は、時計回りまたは反時計回りの方向であると見なすことができます。電流のカスタム方向を選択したら、回路の最終的な解決まで、回路全体に同じ方向を適用して維持する必要があります。
最終的な値が正の値である場合、それは現在の想定される方向が正しいことを意味します。負の値の場合、その方向の電流は、想定されている方向とは逆になります。
キルヒホッフの法則による回路解析
KCLとKVL(キルヒホッフの法則)に関する解決例
例:
R1の抵抗 =10Ω、R 2 =4ΩおよびR3 =8Ωは、示されているように(抵抗が無視できる)最大2つのバッテリーに接続されています。各抵抗器を流れる電流を見つけます。 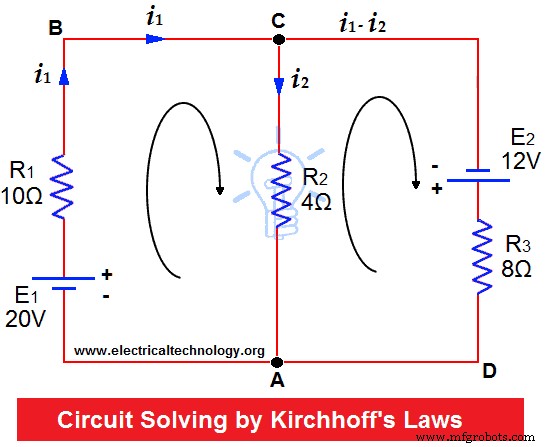
解決策:
電流が矢印で示された方向に流れると仮定します。
ジャンクションCとAにKCLを適用します。
したがって、現在のメッシュABC = i 1
現在のメッシュCA = i 2
次に、メッシュCDAの現在= i 1 – i 2
ここで、メッシュABCにKVLを適用すると、20Vが時計回りに作用します。 IR製品の合計を等しくすると、次のようになります。
10 i 1 + 4 i 2 =20…(1)
メッシュACDでは、12ボルトが時計回りに作用し、次のようになります。
8( i 1 – i 2 )– 4 i 2 =12
8 i 1 – 8 i 2 – 4 i 2 =12
8 i 1 – 12 i 2 =12…(2)
式(1)に3を掛けます;
30 i 1 + 12 i 2 =60
iの解決 1
30 i 1 + 12 i 2 =60
8 i 1 – 12 i 2 =12
___________
38 i 1 =72
上記の方程式は、EliminationまたはCramer’sRuleによって簡略化することもできます。
i 1 =72÷38=1.895アンペア =10オームの抵抗器の電流
(1)にこの値を代入すると、次のようになります。
10(1.895)+ 4 i 2 =20
4 i 2 =20 – 18.95
i 2 =0.263アンペア =4オームの抵抗器の電流。
今、
i 1 – i 2 =1.895 – 0.263 = 1.632 アンペア
キルヒホッフの法則の適用
- キルヒホッフの法則を使用して、電流や電圧などの未知の値の値、および回路内のこれらのクインテットの流れる値の方向を決定できます。
- これらの法則はどの回路にも適用できます*(記事の最後にあるキルヒホッフの法則の制限を参照)が、複雑な回路やネットワークで未知の値を見つけるのに役立ちます。
- 電流と電圧の値を見つけるためにノードとメッシュの分析でも使用されます。
- 各独立ループを流れる電流は、KVL(各ループ)を適用することによって運ばれ、すべての電流をカウントすることによって回路の任意の要素に電流を流します(ループ電流法に適用可能)。
- 各分岐を流れる電流は、回路の各ループにKCL(各ジャンクション)KVLを適用することによって運ばれます(ループ電流法に適用可能)。
- キルヒホッフの法則は、電気回路を介したエネルギーの伝達を理解するのに役立ちます。
知っておきたいこと:
キルヒホッフの法則によって電気回路を単純化および分析する際には、これらの経験則を考慮に入れる必要があります。
- 時計回りの電流によるループ内の電圧降下は、正(+)の電圧降下と見なされます。
- 反時計回りの電流によるループ内の電圧降下は、負(-)の電圧降下と見なされます。
- バッテリーから時計回りに流れる電流は正(+)と見なされます。
- バッテリーから反時計回りに流れる電流は、正(-)と見なされます。
キルヒホッフの法則の制限:
- KCLは、電流が導体とワイヤにのみ流れるという仮定に基づいて適用されます。の高周波回路では、寄生容量を無視できなくなります。このような場合、導体またはワイヤが伝送ラインとして機能しているため、電流が開回路に流れる可能性があります。
- KVLは、閉ループをリンクする変動磁場がないことを前提として適用されます。一方、高周波であるが短波長のAC回路で変化する磁場が存在する場合、電場は保存的なベクトル場ではありません。したがって、電界を電位の勾配にすることはできず、ループの周りの電界の線積分はゼロではなく、KVLと直接矛盾します。そのため、このような状況ではKVLは適用されません。
- 磁場から電場へのエネルギーの伝達中に、回路の周りのP.d(電位差)を0に等しくするためにファッジをKVLに導入する必要があります。
電気回路分析の定理に関する関連記事:
- テブナンの定理。解決された例を使用したステップバイステップの手順
- ノートンの定理。例を使用した簡単なステップバイステップの手順(図解)
- SUPERNODE回路解析|解決された例を使用したステップバイステップ
- SUPERMESH回路解析|解決された例を使用したステップバイステップ
- ACおよびDC回路の最大電力伝達定理
- 補償定理–証明、説明、および解決された例
- 置換定理–解決された例を使用したステップバイステップガイド
- ミルマンの定理– ACおよびDC回路の分析–例
- 重ね合わせの原理–解決された例を使用した回路解析
- テレゲンの定理–解決された例とMATLABシミュレーション
- 分圧器ルール(VDR)– R、L、C回路の解決例
- 現在の分流の法則(CDR)–ACおよびDC回路の解決例
- オームの法則:ステートメントと数式を使用した簡単な説明
- スターからデルタおよびデルタからスターへの変換。 Y-Δ変換
産業技術



