テレゲンの定理–解決された例とMATLABシミュレーション
テレゲンの定理–解決された例を含むステップバイステップガイド
テレゲンの定理とは何ですか?
テレゲンの定理 オランダの電気技師兼発明家BernardD.H. Tellegenによって出版されました この定理は、ネットワーク分析における他の定理の中で最も重要で基本的な定理です。他のほとんどの定理は、この定理から派生しています。
テレゲンの定理は、キルヒホッフの法則に依存しています。したがって、この定理は、キルヒホッフの法則に従うネットワークに適用できます。この定理は、線形または非線形、時変または非変、パッシブまたはアクティブ要素を持つネットワークの広い範囲に適用できます。
テレゲンの定理は次のように述べています;
テレゲンの定理は、エネルギー保存の法則の原理に基づいて機能します。この定理は、物理ネットワークの動的な動作を見つけるために、化学的および生物学的アプリケーションで使用されます。信号処理では、この定理を使用してフィルターを設計します。
- 関連記事:テブナンの定理。解決例を含むステップバイステップガイド
数式
定理の一般的な分析では、ネットワーク内に「n」個の要素が与えられていると見なします。エレメントを流れる瞬時電流はi1 、i 2 、i 3 、…。、i n 。そして、この分岐の瞬時電圧はv 1です。 、v 2 、v 3 、…。、v n 。
したがって、要素1の瞬間的な電流と電圧はi 1です。 およびv1 。瞬時電力(p 1 )この要素によって消費されるのはv 1です i 1 。
p 1 =v 1 i 1
要素2の瞬間的な力は( p 2 );
p 2 =v 2 i 2
同様に、n th の瞬時電力 要素は( p n );
p n =v n i n
テレゲンの定理によると、すべての瞬時電力の合計はゼロです。これは、すべての瞬時電力p 1を合計する必要があることを意味します 、p 2 、p 3 、…。、p n 。
p 1 + p 2 + p 3 +…+p n = 0
v 1 i 1 + v 2 i 2 + v 3 i 3 +…+v n i n = 0
一般的な形式では、k th に対して上記の式を記述できます。 ブランチ;
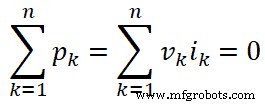
場所
- n =ネットワーク内のブランチの総数
- v k =k th の瞬時電圧 ブランチ
- i k =k th の瞬時電流 ブランチ
- p k =k th の瞬時電力 ブランチ
ここで、ブランチABはブランチkと等しいため、次の図を検討してください。

したがって、瞬時電圧 v k ;
v k =v a – v b
そして、ブランチ(aからb)を通過する瞬間電流は i kです。 ;
i k =i ab
つまり、瞬時電力 p k です;
p k =v k i k =(v a – v b )i ab …..(1)
ここで、瞬間電流の反対方向(bからa)を検討します。
i ab =– i ab
瞬時電圧;
v k =v b – v a
瞬時電力 p k です;
p k =v k i k =(v b – v a )i ba …..(2)
方程式1と2の合計;
2 v k i k =( v a – v b ) i ab +(v b – v a ) i ba
v k i k =1/2 [( v a – v b ) i ab +(v b – v a ) i ba ]…..(3)
この式は、n分岐に対して次のように記述できます;
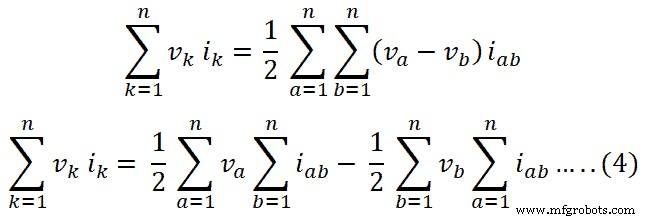
キルヒホッフの現在の法則によれば、回路のノードでは電流の代数的合計はゼロです。
したがって、
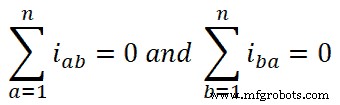
この値を式-4に入れると、次のようになります;
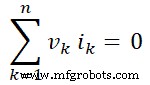
したがって、ネットワークに供給される電力の合計がゼロであることが証明されます。したがって、それはテレゲンの定理であることが証明されています。また、ネットワークの要素によって吸収される電力の合計は、ソースによって供給される電力の合計に等しいと説明されています。
- 関連記事:ノートンの定理。解決例を含むステップバイステップガイド
テレゲンの定理に従うための手順
テレゲンの定理によって電気回路網を解決するには、以下の手順に従う必要があります。
ステップ1: 与えられた電気ネットワークでいくつかのブランチを見つける必要があります。次に、各ブランチで電力が消費されることを確認します。電力を見つけるには、従来の分析方法を使用して、その分岐の電圧または電流を見つける必要があります。
ステップ2: 各ブランチの瞬時電力を見つけます。
ステップ3: 電力供給ブランチと見なされるエネルギー源を持つブランチ。そして、ブランチには他の要素があり、電力吸収ブランチと見なされます。次に、電力供給ブランチと電力吸収ブランチを特定します。
ステップ4: 電力供給ブランチで正の符号があり、電力吸収ブランチで負の電圧降下があると仮定します。逆符号も想定できます。ただし、例全体で変更することはできません。
ステップ5: テレゲンの定理を正当化するには、すべてのブランチから計算されたすべてのパワーを追加する必要があります。そして、この合計は常にゼロです。
- 関連記事:SUPERMESH回路解析–解決された例を使用したステップバイステップ
例を挙げて理解しましょう。
テレゲンの定理の解決例
例1
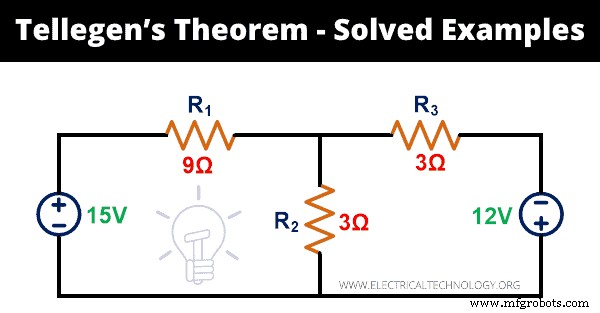
以下のネットワークに対するテレゲンの定理を正当化します。
解決策:
ステップ1: 特定の回線ネットワークには5つのブランチがあります。瞬時電力を計算するには、各分岐を流れる電流を見つける必要があります。そのために、KVLをネットワークに適用します。
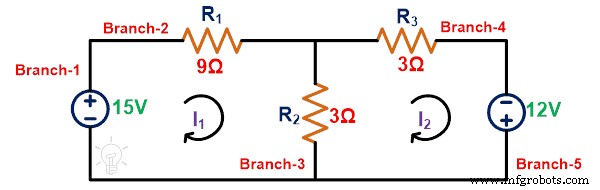
ループ1にKVLを適用します;
15 =12 I 1 –3私 2
ループ2にKVLを適用します;
12 =–3私 2 +6私 2
上記の方程式を解くことにより、ループ電流I 1の値を見つけることができます。 およびI2 。そして、これらの値は次のとおりです。
私 1 =2A
私 2 =3A
ステップ2: ブランチ3を通過する電流は;
私 1 2 =私 2 –私 1 =3 – 2 =1A
すべてのブランチに電流が流れています。次に、各ブランチのパワーを見つけます。
P 1 = V I 1 =15 x 2 =30W
P 2 = R 1 私 1 2 =9 x 4 =36W
P 3 = R 1 私 12 2 =3 x 1 =3W
P 4 = R 3 私 2 2 =3 x 9 =27W
P 5 = V I 2 =12 x 3 =36W
ステップ3: ソースを持つ2つのブランチがあります。これらのブランチは電力供給ブランチであり、他の3つのブランチは電力吸収ブランチです。
ここでは、この例では、電力供給ブランチの符号が正で、電力吸収ブランチの符号が負であると想定しています。したがって、ブランチ1と5は電力供給ブランチであり、他のブランチは電力吸収ブランチです。
ステップ4: 力のしるしP1 およびP5 正(電力供給ブランチ)であり、P 2の符号 、P 3 、およびP 4 負です(電力吸収ブランチ)。
ステップ5: ここで、すべてのブランチによって消費される電力の合計を見つける必要があります。
P 1 – P 2 – P 3 – P 4 + P 5 =30W – 36W – 3W – 27W + 36W =0W
したがって、瞬時電力の合計はゼロです。したがって、この定理が証明されます。
- 関連記事:SUPERNODE回路分析–解決された例を使用したステップバイステップ
例2
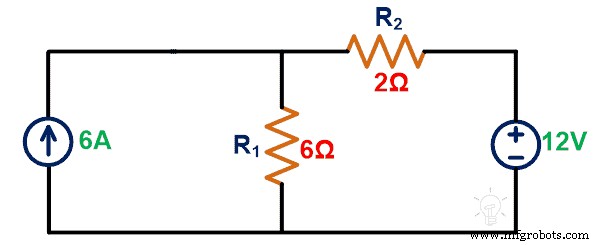
テレゲンの定理を使用して、6Aの電流源の両端の電圧を求めます。
解決策:
ステップ1: 要素を通過する電圧または電流を計算する必要があります。そのために、特定のネットワークにKCLまたはKVLを適用します。
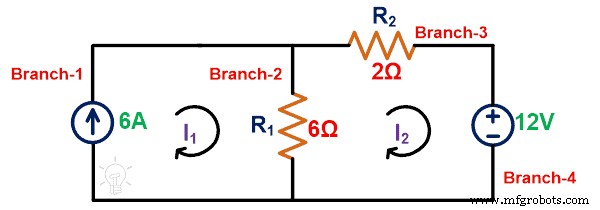
ループ2にKVLを適用します;
-12 =8私 2 –6私 1
現在のソースを持つブランチを通過する現在のパスは I 1 ;
私 1 =6A
この値を上記の式に入れます;
-12 =8私 2 – 6(6)
-12 =8私 2 – 36
36 – 12 =8私 2
24 =8私 2
私 2 =3A
ステップ2: 電流はブランチを通過します-2は;
私 12 =私 1 –私 2 =6 – 3 =3A
次に、各ブランチの力を見つけます;
P 1 = V I 1 = V x 6 =6 x V
P 2 = R 1 私 12 2 =6 x 9 =54W
P 4 = R 2 私 2 2 =2 x 9 =18W
P 4 = V I 2 =-12 x 3 =-36W
ステップ3: ここでは、エネルギー源を持つ2つのブランチがあります。したがって、これらのブランチを電力供給ブランチと見なす必要があります。そして、正の符号を瞬時電力に設定します。
他の2つのブランチには抵抗のみがあります。したがって、これらの分岐は電力吸収分岐であり、瞬時電力に負の符号を設定します。
ステップ4: パワーP1 およびP4 正の符号とパワーP2 およびP3には負の符号があります。
ステップ5: ここで、すべての瞬時電力を合計する必要があります。
P 1 – P 2 – P 3 + P 4 =0W
P 1 – 54 – 18 + 36 =108W
6A電流源から供給される電力は108Wです。したがって、電流源の両端の電圧は次のように計算されます。
P 1 = V I
108W =V x 6A
V =18V
したがって、電流源の両端の電圧は18Vです。
- 関連記事: ACおよびDC回路の最大電力伝達定理
MATLABを使用したテレゲンの定理の分析とシミュレーション
目的:
上記の例で示した回路図のテレゲンの定理を証明します。
要件: MATLAB
理論:
テレゲンの定理によると、すべての分岐の瞬時電力の合計はゼロに等しくなります。この定理を証明するには、すべてのブランチの瞬時電力を計算する必要があります。
瞬時電力を見つけるには、すべての分岐の電圧または電流を計算する必要があります。そのために、KCLまたはKVLの定理を使用できます。ただし、ここでは、MATLABSimulinkモデルを使用して電流と電圧を見つけます。
multisim、psimなどの他のソフトウェアも使用できます。Simulinkモデルで回路図を作成します。 Simulinkモデルにより、各ブランチの電圧と電流を見つけることができます。
その後、電圧と電流から瞬時電力を見つけることができます。一部のソフトウェアから瞬時電力を直接見つけることができます。
MATLABSimulinkモデル
次の図は、上記の例の回路図を示しています。
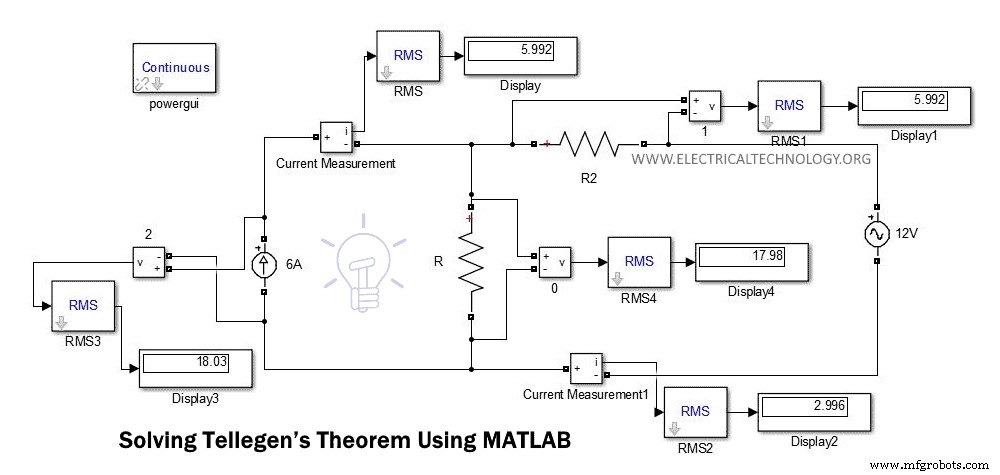
この図では、ディスプレイから電圧と電流を直接見つけることができます。 KCLまたはKVLを使用して電圧と電流を計算することにより、これらの値を比較できます。
計算
電圧または電流を計算した後、瞬時電力を見つけることができます。または、ソフトウェアから瞬時電力を直接見つけることができます。必要なのは瞬時の電力だけです。その後、すべての力を追加する必要があります。
パワーの合計は常にゼロです。この例では、Simulinkから検出された電圧と電流の値と、KVLとKCLを使用して前の例で計算された同じ値を比較します。これらの値は同じです。
これらの値は、ブレッドボード上の接続抵抗とソースによっても計算されます。また、電圧計と電流計を使用して、すべての分岐を通過する電圧と電流を測定できます。
したがって、テレゲンの定理が証明されています。
- 関連記事:キルヒホッフの電流および電圧法(KCLおよびKVL)|解決した例
テレゲンの定理の適用
この定理は非常に基本的であり、回路解析で広く使用されています。この定理には多くの応用があります。いくつかのアプリケーションを以下に示します。
- フィルターを設計する場合、この定理はデジタル信号処理のアプリケーションで非常に役立ちます。
- 化学プラントの安定性を判断するために、この定理は化学工学で使用されます。
- この定理は、線形-非線形、アクティブ-パッシブ、時変/時不変の要素を持つ一括システムに適用されます。
- この定理は生物学的プロセスで使用されます。
- トポロジと構造反応の分析に使用されます。
- これは、物理ネットワークの動的な動作を見つけるためにも使用されます。
関連する電気回路解析チュートリアル:
- 重ね合わせの原理–解決例を用いた回路解析
- クラメルの公式計算機–電気回路用の2および3方程式システム
- 電気電子工学計算機
- 5000以上の電気電子工学の公式と方程式
産業技術



