MATLAB-統合
統合は、本質的に異なる 2 つのタイプの問題を扱います。
- <リ>
最初のタイプでは、関数の微分が与えられ、関数を見つけたいと考えています。したがって、基本的に微分のプロセスを逆にします。この逆のプロセスは、反微分、原始関数の発見、または不定積分の発見として知られています。 .
<リ>2 番目のタイプの問題は、非常に多数の非常に小さな量を合計し、項の数が無限になる傾向がある一方で、量のサイズがゼロに近づくにつれて極限を取ることを伴います。このプロセスは、定積分の定義につながります .
定積分は、面積、体積、重心、慣性モーメント、力によって行われる仕事、および他の多くの用途を見つけるために使用されます。
MATLAB を使用した不定積分の検出
定義により、関数 f(x) の導関数が f'(x) である場合、x に関する f'(x) の不定積分は f(x) であると言います。たとえば、x 2 の (x に関する) 導関数は は 2x です。2x の不定積分は x 2 であると言えます。 .
記号で −
f'(x 2 ) =2x したがって、
∫ 2xdx =x 2 .
x 2 の導関数のため、不定積分は一意ではありません。 + c (定数 c の任意の値) も 2x になります。
これを記号で表すと −
∫ 2xdx =x 2 +c .
ここで、c は「任意定数」と呼ばれます。
MATLAB は int を提供します。 式の積分を計算するコマンド。関数の不定積分の式を導出するには、次のように記述します −
int(f);
たとえば、前の例から −
syms x int(2*x)
MATLAB は上記のステートメントを実行し、次の結果を返します −
ans = x^2
例 1
この例では、一般的に使用されるいくつかの式の積分を見つけてみましょう。スクリプト ファイルを作成し、その中に次のコードを入力します −
syms x n int(sym(x^n)) f = 'sin(n*t)' int(sym(f)) syms a t int(a*cos(pi*t)) int(a^x)
ファイルを実行すると、次の結果が表示されます-
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a)
例 2
スクリプト ファイルを作成し、その中に次のコードを入力します −
syms x n int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))
かなり 関数は、より読みやすい形式で式を返します。
ファイルを実行すると、次の結果が表示されます-
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2
MATLAB を使用した定積分の検出
定義上、定積分は基本的に和の極限です。定積分を使用して、曲線と x 軸の間の領域や 2 つの曲線の間の領域などの領域を見つけます。定積分は、必要な量を合計の極限として表すことができる他の状況でも使用できます。
整数 関数は、積分を計算したい範囲を超えることにより、定積分に使用できます。
計算する
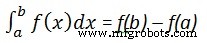
int(x, a, b)
たとえば、次の値を計算するには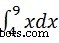 
書き込みます −
int(x, 4, 9)
MATLAB は上記のステートメントを実行し、次の結果を返します −
ans = 65/2
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));
Octave はコードを実行し、次の結果を返します −
Area: 32.500
次のように、Octave が提供する quad() 関数を使用して、別の解決策を与えることができます −
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));
Octave はコードを実行し、次の結果を返します −
Area: 32.500
例 1
x 軸と曲線 y =x 3 で囲まれた面積を計算してみましょう。 −2x+5 と縦座標 x =1 と x =2.
必要な面積は −
で与えられます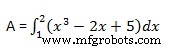
スクリプト ファイルを作成し、次のコードを入力します −
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));
ファイルを実行すると、次の結果が表示されます-
a = 23/4 Area: 5.7500
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));
Octave はコードを実行し、次の結果を返します −
Area: 5.7500
次のように、Octave が提供する quad() 関数を使用して、別の解決策を与えることができます −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));
Octave はコードを実行し、次の結果を返します −
Area: 5.7500
例 2
曲線の下の面積を求めます:f(x) =x 2 −4 ≤ x ≤ 9 の cos(x)。
スクリプト ファイルを作成し、次のコードを記述します −
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
ファイルを実行すると、MATLAB はグラフをプロットします −
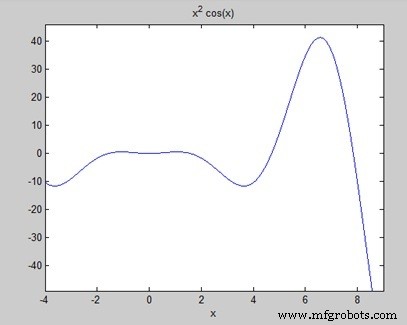
出力は以下のとおりです −
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));
MATLAB