MATLAB-微積分

MATLAB は、微分および積分計算の問題を解くためのさまざまな方法を提供し、任意の次数の微分方程式を解き、極限を計算します。何よりも、元の関数とその導関数を解くことで、複雑な関数のグラフを簡単にプロットし、グラフ上の最大値、最小値、およびその他の定常点を確認できます。

この章では、微積分の問題を扱います。この章では、計算前の概念、つまり関数の極限の計算と極限の特性の検証について説明します。

次の章では差分、式の導関数を計算し、グラフの極大値と極小値を見つけます。微分方程式の解法についても説明します。

最後に、統合での章では、積分計算について説明します。

制限の計算

MATLAB は制限を提供します制限を計算する関数。最も基本的な形式では、制限関数は式を引数として取り、独立変数がゼロになるときの式の極限を見つけます。

たとえば、関数 f(x) =(x³ の極限を計算してみましょう。 + 5)/(x⁴ + 7)、x がゼロになる傾向があるため。

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB は上記のステートメントを実行し、次の結果を返します −

ans =
   5/7

limit 関数は、シンボリックコンピューティングの領域に入ります。 syms を使用する必要があります関数を使用して、使用しているシンボリック変数を MATLAB に伝えます。変数はゼロ以外の数値になる傾向があるため、関数の制限を計算することもできます。 lim _x->a を計算するには (f(x))、引数を指定して limit コマンドを使用します。 1 つ目は式で、2 つ目は x という数値です。近づいてきました。ここは a です .

たとえば、関数 f(x) =(x-3)/(x-1) の極限を計算してみましょう。x は 1 になる傾向があるためです。

limit((x - 3)/(x-1),1)

MATLAB は上記のステートメントを実行し、次の結果を返します −

ans =
   NaN

別の例を見てみましょう。

limit(x^2 + 5, 3)

MATLAB は上記のステートメントを実行し、次の結果を返します −

ans =
   14

Octave を使用した制限の計算

以下は、symbolic を使用した上記の例の Octave バージョンです。パッケージ、実行して結果を比較してみてください −

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave は上記のステートメントを実行し、次の結果を返します −

ans =
   0.7142857142857142857

極限の基本特性の検証

代数極限定理は、極限のいくつかの基本的な性質を提供します。これらは次のとおりです-

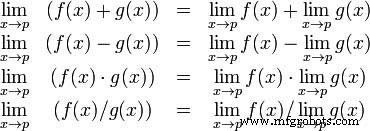
2 つの関数を考えてみましょう −

f(x) =(3x + 5)/(x - 3)
g(x) =x² + 1.

x が 5 になる関数の極限を両方の関数で計算し、これら 2 つの関数と MATLAB を使用して極限の基本的な特性を検証してみましょう。

例

スクリプトファイルを作成し、次のコードを入力します −

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

ファイルを実行すると、表示されます-

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Octave を使用した極限の基本特性の検証

以下は、symbolic を使用した上記の例の Octave バージョンです。パッケージ、実行して結果を比較してみてください −

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave は上記のステートメントを実行し、次の結果を返します −

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

左右の制限

関数が変数の特定の値に対して不連続性を持つ場合、その時点では極限は存在しません。言い換えると、関数 f(x) の極限は x =a で不連続になります。x が左側から x に近づくときの極限の値が、x が右側から近づくときの極限の値と等しくない場合です。

これは、左利きと右利きの制限の概念につながります。左手極限は、左から x -> a の極限として定義されます。つまり、x a の値に対して、右から x -> a の極限として定義されます。つまり、x が a に近づきます。左利きの極限と右利きの極限が等しくない場合、極限は存在しません。

関数を考えてみましょう−

f(x) =(x - 3)/|x - 3|

その lim_x->3 を示します f(x) は存在しません。 MATLAB は、この事実を 2 つの方法で確立するのに役立ちます −

関数のグラフをプロットし、不連続性を示す
限界を計算し、両者が異なることを示す

左側と右側の制限は、文字列 'left' と 'right' を最後の引数として limit コマンドに渡すことによって計算されます。

例

スクリプトファイルを作成し、次のコードを入力します −

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

ファイルを実行すると、MATLAB は次のプロットを描画します

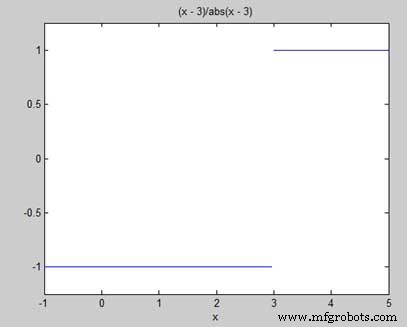
この次の出力が表示された後-

l =
   -1
  
r =
   1

MATLAB-代数 MATLAB-微分

MATLAB