MATLAB-微分
MATLAB は diff を提供します 記号導関数を計算するコマンド。最も単純な形式では、微分したい関数を引数として diff コマンドに渡します。
たとえば、関数 f(t) =3t 2 の導関数を計算してみましょう。 + 2t -2
例
スクリプト ファイルを作成し、次のコードを入力します −
syms t f = 3*t^2 + 2*t^(-2); diff(f)
上記のコードをコンパイルして実行すると、次の結果が生成されます −
ans = 6*t - 4/t^3
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave はコードを実行し、次の結果を返します −
ans = -(4.0)*t^(-3.0)+(6.0)*t
初等微分規則の検証
関数を微分するためのさまざまな方程式またはルールを簡単に述べ、これらのルールを検証しましょう。この目的のために、一次微分を f'(x) と書き、二次微分を f"(x) と書きます。
以下は差別化のルールです −
ルール 1
任意の関数 f と g および任意の実数 a と b について、関数の導関数です −
h(x) =af(x) + bg(x) x に関しては −
で与えられるh'(x) =af'(x) + bg'(x)
ルール 2
合計 と引き算 規則では、f と g が 2 つの関数である場合、f' と g' はそれぞれその導関数であると述べられています。
(f + g)' =f' + g'
(f - g)' =f' - g'
ルール 3
製品 ルールは、f と g が 2 つの関数である場合、f' と g' はそれぞれそれらの導関数であると述べています。
(f.g)' =f'.g + g'.f
ルール 4
商 ルールは、f と g が 2 つの関数である場合、f' と g' はそれぞれそれらの導関数であると述べています。
(f/g)' =(f'.g - g'.f)/g 2
ルール 5
多項式 または初等べき乗則は、y =f(x) =x n の場合、 の場合、f' =n です。 x (n-1)
この規則の直接的な結果は、定数の導関数がゼロになることです。つまり、y =k の場合です。 、任意の定数、その後
f' =0
ルール 6
チェーン ルールは、関数 h(x) =f(g(x)) の関数の導関数を示しています xに関しては、
h'(x)=f'(g(x)).g'(x)
例
スクリプト ファイルを作成し、次のコードを入力します −
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
ファイルを実行すると、MATLAB は次の結果を表示します −
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave はコードを実行し、次の結果を返します −
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
指数関数、対数関数、三角関数の導関数
次の表は、一般的に使用される指数関数、対数関数、三角関数の導関数を示しています −
| 機能 | 派生物 |
|---|---|
| c a.x | c a.x .ln c.a (ln は自然対数) |
| e x | e x |
| ln x | 1/x |
| lnc × | 1/x.ln c |
| x x | x x .(1 + ln x) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | 秒 2 (x)、または 1/cos 2 (x)、または 1 + tan 2 (x) |
| ベビーベッド(x) | -csc 2 (x)、または -1/sin 2 (x)、または -(1 + ベビーベッド 2 (x)) |
| 秒(x) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
例
スクリプト ファイルを作成し、次のコードを入力します −
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
ファイルを実行すると、MATLAB は次の結果を表示します −
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave はコードを実行し、次の結果を返します −
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
高次導関数の計算
関数 f の高次導関数を計算するには、構文 diff(f,n) を使用します .
関数 y =f(x) =x .e -3x の 2 次導関数を計算してみましょう。
f = x*exp(-3*x); diff(f, 2)
MATLAB はコードを実行し、次の結果を返します −
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave はコードを実行し、次の結果を返します −
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
例
この例では、問題を解いてみましょう。関数 y =f(x) =3 sin(x) + 7 cos(5x) .方程式 f" + f =-5cos(2x) かどうかを調べる必要があります。
スクリプト ファイルを作成し、次のコードを入力します −
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
ファイルを実行すると、次の結果が表示されます-
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave はコードを実行し、次の結果を返します −
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
曲線の最大値と最小値を見つける
グラフの極大値と極小値を検索する場合、基本的には、特定の場所での関数のグラフ上の最高点または最低点、またはシンボリック変数の値の特定の範囲を探しています。
関数 y =f(x) の場合、グラフの傾きがゼロであるグラフ上の点は 静止点 と呼ばれます .つまり、静止点は f'(x) =0 の場所です。
微分した関数の定常点を見つけるには、導関数をゼロに設定して方程式を解く必要があります。
例
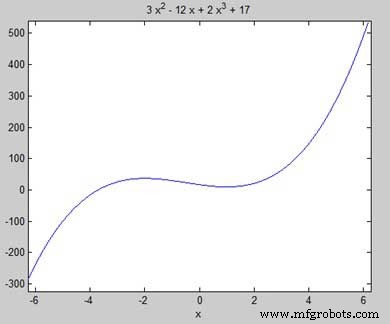
関数 f(x) =2x 3 の停留点を見つけてみましょう。 + 3x 2 − 12x + 17
次の手順を実行します −
まず、関数を入力してそのグラフをプロットしましょう。
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB はコードを実行し、次のプロットを返します −
上記の例と同等の Octave コードを次に示します −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
私たちの目的は、グラフ上で局所的な最大値と最小値を見つけることなので、グラフ上の区間 [-2, 2] の局所的な最大値と最小値を見つけてみましょう。
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB はコードを実行し、次のプロットを返します −
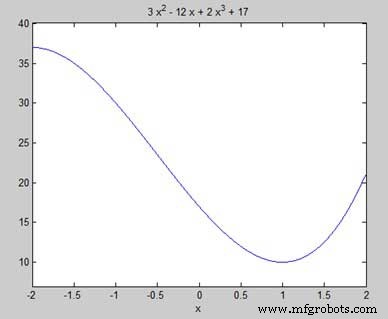
上記の例と同等の Octave コードを次に示します −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
次に導関数を計算しましょう
g = diff(y)
MATLAB はコードを実行し、次の結果を返します −
g = 6*x^2 + 6*x - 12
上記の計算に相当するオクターブは次のとおりです-
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave はコードを実行し、次の結果を返します −
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
微分関数 g を解いて、ゼロになる値を求めましょう。
s = solve(g)
MATLAB はコードを実行し、次の結果を返します −
s = 1 -2
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave はコードを実行し、次の結果を返します −
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
これは私たちの筋書きと一致しています。それでは、臨界点 x =1, -2 で関数 f を評価してみましょう。 subs を使用して、シンボリック関数の値を置き換えることができます コマンド。
subs(y, 1), subs(y, -2)
MATLAB はコードを実行し、次の結果を返します −
ans = 10 ans = 37
以下は、上記の計算に相当するオクターブです-
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
したがって、関数 f(x) の最小値と最大値 =2x 3 + 3x 2 − 12x + 17、区間 [-2,2] は 10 と 37 です。
微分方程式を解く
MATLAB は dsolve を提供します。 微分方程式をシンボリックに解くためのコマンド。
dsolve の最も基本的な形式 単一の方程式の解を求めるコマンドは
dsolve('eqn')
ここで eqn 方程式を入力するために使用されるテキスト文字列です。
これは、MATLAB が C1、C2 などのラベルを付ける一連の任意の定数をもつシンボリック ソリューションを返します。
問題の初期条件と境界条件を指定することもできます。式に続くコンマ区切りのリストとして、-
dsolve('eqn','cond1', 'cond2',…)
dsolve コマンドを使用する目的で、導関数は D で示されます .たとえば、f'(t) =-2*f + cost(t) のような式は −
と入力されます。'Df =-2*f + cos(t)'
高次の導関数は、導関数の順序で D に続くことで示されます。
たとえば、式 f"(x) + 2f'(x) =5sin3x は −
として入力する必要があります。'D2y + 2Dy =5*sin(3*x)'
一階微分方程式の簡単な例を取り上げましょう:y' =5y.
s = dsolve('Dy = 5*y')
MATLAB はコードを実行し、次の結果を返します −
s = C2*exp(5*t)
二階微分方程式の別の例を取り上げましょう:y" - y =0, y(0) =-1, y'(0) =2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB はコードを実行し、次の結果を返します −
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB



