第一原理からの窒素ドープ単分子層MoS2における光ガルバニック効果

はじめに

新しい材料を探し、それらのエキゾチックな特性を探求することは、現代物理学の主要なテーマを構成します。現在、単層二硫化モリブデン（MoS ₂ ）に大きな関心が寄せられています。 ）、これはグラフェンと同様に、機械的に剥離することができます[1、2]。バルクMoS ₂ とは対照的 これは、間接バンドギャップ半導体である単分子層MoS ₂ に属します。 は、大きなバンドギャップを持つ直接バンドギャップ半導体[3]です。単層MoS ₂ 強力な光吸収[5–8]や高いキャリア移動度などの優れた光学的および電気的特性[4]を備えており、トランジスタ[9]や超高感度光検出器[10]での重要なアプリケーションを約束します。さらに、最近のab initio研究は、単分子層MoS ₂ の電子的および磁気的特性を調整する可能性を示しています[11–19] ドーピングにより、潜熱容量の大きいスピントロニクスデバイスへの道を開く[20]。

材料が光で照らされたときに電流が誘導される光ガルバニック効果（PGE）は、空間反転対称性が壊れた半導体で発生する可能性があります。 PGEは、円形または線形偏光のいずれかによって誘導できます。これらの光は、それぞれ円形光起電力効果（CPGE）および線形光起電力効果（LPGE）として造られています。最近、PGEはいくつかの新しい材料で観察されています[21–26]。たとえば、GaAs / AlGaAs（二次元電子ガスの一種）は、LPGEとCPGEの両方を示すことがわかっています[27]。 CPGEは、HgTe量子井戸やSb ₂ などのトポロジカル絶縁体[28–30]にも見られます。 Te ₃ 。注目すべきことに、CPGEはいくつかのワイル半金属で報告されています[31–33]。さらに、グラフェンPN接合およびSドープ単分子層黒リン[34–36]の光応答が、Guoのチームによって分析されました。興味深いことに、LPGEとCPGEの両方が、光電流が消失するゼロ点を示す可能性があります。ただし、これらのゼロ点につながるメカニズムについては、未解決の問題が残っています。

単層MoS ₂ でのドーピング 実験[37–40]と理論[11、41、42]によって、特に窒素をドープした単分子層MoS ₂ について分析されています。 [38、43]。この作業では、窒素をドープした単分子層MoS ₂ のPGEの第一原理研究を実施します。 。材料はCPGEとLPGEの両方を示し、これらは空間的に異方性であり、ゼロ点を示します。結合状態密度（JDOS）とバンド構造を組み合わせた分析により、光電流の振る舞いに関する詳細な調査を提供します。特に、LPGEとCPGEのゼロ点は異なるメカニズムから生じることがわかります。前者は前者の禁制遷移によって引き起こされますが、後者はラシュバとドレスルハウスのスピン軌道相互作用の存在下での全スピンスリットのゼロによるものです。 。

モデルとメソッド

まず、CASTEPパッケージ[44、45]で最適な形状が実行されます。窒素ドープ単層MoS ₂ のユニットセル用 、一般化勾配近似（GGA）およびPerdew-Burke-Ernzerhof（PBE）パラメーター化が交換および相関ポテンシャルに採用されました。高精度の構造を得るために、平面波のエネルギーカットオフを500eVとした。逆格子空間では、6×12×1のk点が考慮されました。総エネルギーは10 ^-6 に収束します e V また、各原子の残留力は0.01 \（eV / \ mathop A \ Limits ^ \ circ \）未満です。

次に、量子トランスポートパッケージ Nanodcal [46、47]は、JDOSとバンド構造のセルフコンシステント計算に使用され、 G で補完されています。 G A _ P B E 交換相関汎関数の場合は96。ここでは、二重ゼータ分極（DZP）原子軌道基底を使用して、すべての物理量を拡張しました。最後に、デバイスの光電流は、グリーン関数形式と密度汎関数理論（NEGF-DFT）の範囲内で計算されました。

2プローブデバイスのアーキテクチャを図1に示します。そこでは、硫黄原子に窒素原子がドープされており、それらの比率は16：1であるため、空間反転対称性が壊れています。図1aは、散乱領域に39個の原子を含む鏡面対称性を示すデバイスを示しています。構造最適化後に得られた緩和された構成であるその側面図[図1bを参照]は、窒素をドープした単分子層MoS ₂ のサンドイッチ構造を示しています。 。

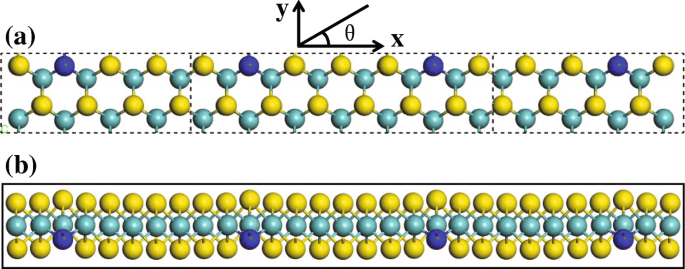
a 窒素をドープしたMoS ₂ の光電流を計算するための2プローブデバイス構造 。 b a のリラックスした構成の側面図 。 S、Mo、およびN原子は、それぞれ黄色、水色、および濃い青で表されます。バイアス電圧がない場合、散乱領域は偏光によって垂直に照射されます。直線偏光の場合、偏光角θ 輸送方向に関して測定されます

窒素ドープ単分子層MoS ₂ の散乱領域の原子 光を垂直に照射しました。この偏光ベクトルは、一般的に次のように記述できます。

ここで、θ 直線偏光の偏光角 ϕ にラベルを付けます は楕円偏光のヘリシティを表す位相角であり、 e _α （α =1,2）は単位ベクトルを示します。 ϕ に注意してください =±45 ^∘ 右/左の円偏光に対応し、 ϕ =0は直線偏光に対応します。検討対象のサンプルでは空間反転対称性が破られているため、PGEを生成できます。 1つのリード線から中央領域への電流を< I で表します 〉 ^{（ p h ）} 、< I を計算します 〉 ^{（ p h ）} 量子トランスポートパッケージ Nanodcal でNEGF-DFTを使用 [46、47]。対応する正規化された光電流は次の式で与えられます

ここで、私 _ω は、単位面積あたりの単位時間あたりの光子の数、つまり光子束です[参考文献を参照してください。 [34–36、48]]。 Nanodcal 、左電極の光電流\（I_ {L} ^ {（ph）} \）は[34]

ここで G ^{<（ p h ）} および G ^{>（ p h ）} はそれぞれグリーン関数が小さく、グリーン関数が大きい（電子-光子相互作用がある）。 Γ _L 散乱領域と左電極の結合を示します。直線偏光の場合、光電流は次の式で与えることができます

円偏光の場合は、

両方とも、\（G_ {1} ^ {^ {> / <\ left（{ph} \ right）}} \）と\（G_ {2} ^ {^ {> / <\ left（{ph} \ right）}} \）は次のように同じ表現になります

ここで、\（G_ {0} ^ {a} \）と\（G_ {0} ^ {r} \）は、それぞれ高度なグリーン関数と遅延したグリーン関数です（フォトンなし）。 p _{α / β} 電子運動量のデカルト成分を表します。 e _{1/2 β} 単位ベクトルのデカルト成分を示します。 N はフォトンの数です。 \（{C_ {0}} ={I _ {\ omega}} {\ left（{e / {m_ {0}}} \ right）^ {2}} \ hbar \ sqrt {{\ mu _ {r} } {\ varepsilon _ {r}}} / 2N \ omega \ varepsilon c \）、ここで c は速度であり、ω 光の周波数です。 ε およびε _r それぞれ誘電率と比誘電率です。 μ _r 相対磁化率を示します。 m ₀ 裸の電子質量を表します。直線偏光の場合

円偏光の場合

その後のPGEの分析における重要な要素は、占有価電子帯と非占有伝導帯の電子状態間の許容光学遷移の数を測定するJDOSです[49–53]。周波数ωの光子による励起に対応するJDOS によって与えられます

ここで E _c （ k ）および E _v （ k ）運動量 k での電子状態のエネルギーを示します それぞれ伝導帯と価電子帯で。非縮退バンドを持つ2次元システムの場合、JDOSは次のように書き直されます

結果と考察

図2は、単分子層MoS ₂ のバンド構造を示しています。 および窒素ドープ単分子層MoS ₂ 。以前の文献では、単層MoS ₂ は、バンドギャップが1.90 eVのダイレクトギャップ半導体です[3、4]。ドーピング前とドーピング後のバンド構造を比較するために、ブリルアンゾーンで同じパスを選択します。窒素ドープ単分子層MoS ₂ の場合 、フェルミ準位を横切る不純物誘起バンドが観察され、これは価電子帯の上部に近い[図2bを参照]。したがって、窒素をドープした単分子層MoS ₂ p型半導体です。重要なのは、空間反転対称性が壊れているため、元の単分子層MoS ₂ のエネルギーバンドです。 外部電圧がなくても、ドーピングの存在下でさらに分割されます。知られているように、そのようなエネルギーバンドの分割は、円偏光による照射下でのスピン軌道相互作用を可能にし、CPGEに重要なメカニズムを提供します。

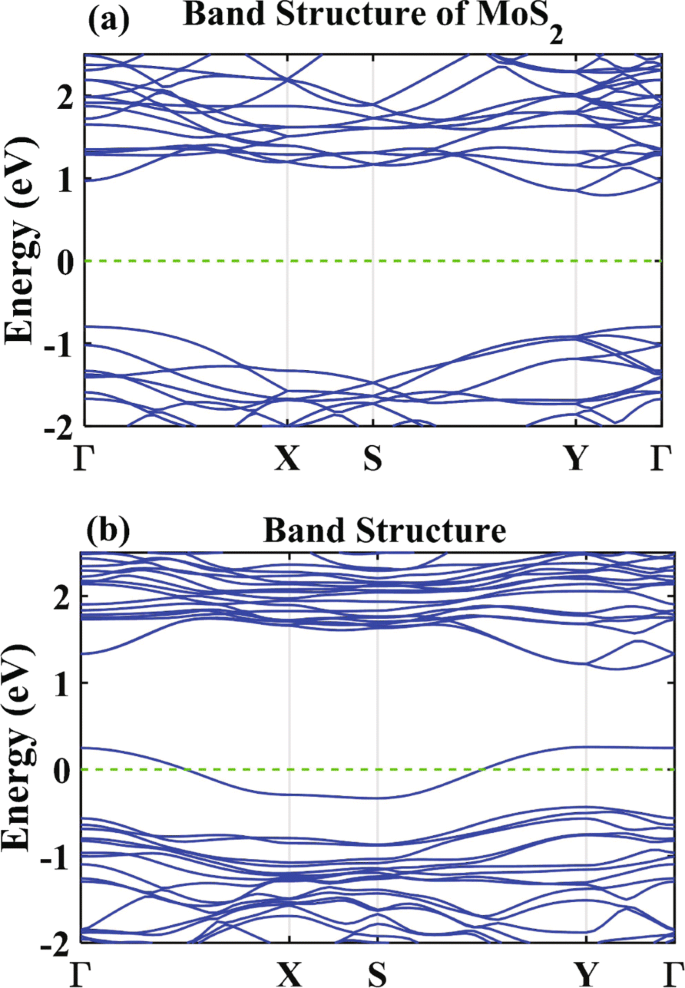
a のバンド構造 単層MoS ₂ および b 窒素ドープ単分子層MoS ₂

ここで、窒素をドープした単分子層MoS ₂ の光応答を研究します。 NEGF-DFT計算によって得られた光による垂直照射下。図3にLPGEとCPGEの光応答関数を示します。 LPGEの場合、θ =π / 4および ϕ =0 ^∘ 。 CPGEの場合、θ =0 ^∘ および ϕ =π / 4。光子エネルギーの範囲は0〜2.3 eV（0.1 eVの間隔）です。図3では、窒素をドープした単分子層MoS ₂ におけるCPGEの光応答 LPGEより2桁強力です。 LPGEの光応答は、レジーム全体で非常に小さいままです。これは、デバイス構造の対称性の直接的な結果です。対照的に、CPGEは0.7 eVの後に発生します。これは、高対称点Yでの不純物バンドと伝導帯の間のエネルギーギャップに近くなります[図2bを参照]。これは、電子遷移が直接であることを意味します。さらに、CPGEは、光子エネルギーが1.7eVを超えると重要になります。光子エネルギーがさらに増加すると、光応答の大きさは非線形に変化し、その方向は正から負に切り替わります。

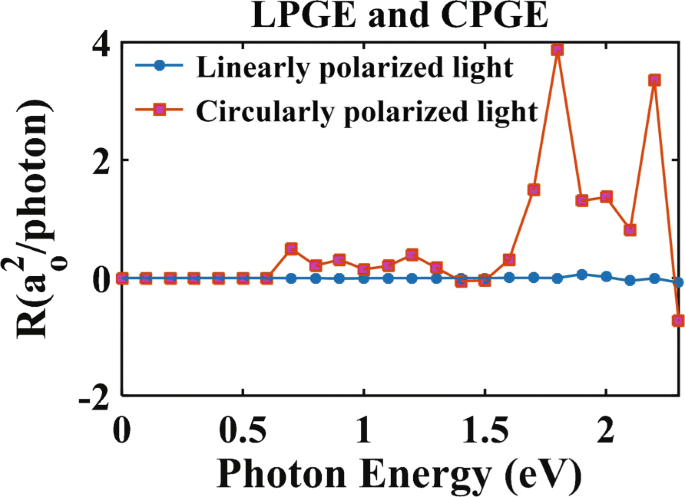
それぞれ直線偏光と円偏光のエネルギーによる光応答関数の変化。 LPGEの場合、θ =π / 4および ϕ =0 ^∘ 。 CPGEの場合、θ =0 ^∘ および ϕ =π / 4。光子エネルギーの範囲は0〜2.3 eVで、間隔は0.1eVです

上記の現象を直感的に理解するために、光電流は光吸収係数αと密接に関連していることに注意してください。 によって定義される

ここでは、 n は屈折率、 c ₀ は真空中の光速を示し、 m _e 電子の質量にラベルを付けます。さらに、 s 電磁波のベクトルポテンシャルの単位ベクトルを示します。マトリックス要素 M _cv 運動量 p に対応します 〈 c の形式です 、 k | p | v 、 k 〉、| v （ c ）、 k 〉準運動量 k での電子状態 価電子帯（伝導帯）で。光電流の発生にはαが必要であることに注意してください> 0。式（12）は、光電流が両方の量に決定的に依存することを意味します。マトリックス要素 M _cv とJDOS。

図4に、サンプルのJDOSを示します。 JDOSは、0.5 eV未満の光子エネルギーではほとんど消滅します。これは、電子がほとんど励起されないことを示しています。ただし、光子エネルギーが0.5 eVを超えると、JDOSに一連のピークが発生します。図4では、光子エネルギー0.69 eVと0.76eVで2つのピークが発生します（緑色の点線を参照）。これは、対称性の高い点YとΓで価電子帯から不純物帯に電子を励起するための最小エネルギーに対応します。 それぞれ[図2bを参照]。さらに、光子エネルギーが0.94 eV、1.03 eV、および1.925eVの値をとるときにもピークが観察されます。それらは、高対称点Y、Γでの不純物バンドから伝導帯への電子の光励起に対応します。 、およびSそれぞれ。さらに、1.65eVと1.89eVのピーク（黒い点線）は、対称性の高い点YとΓでの価電子帯から伝導帯への電子遷移に対応します。 それぞれ。 1.89 eV以降、JDOSは指数関数のように急激に増加し、その傾向は光吸収率の実験と一致しています[40]。その上、我々の結果は、窒素をドープした単分子層MoS ₂ 可視光の範囲で強い光吸収があり、これも実験結果と一致しています。

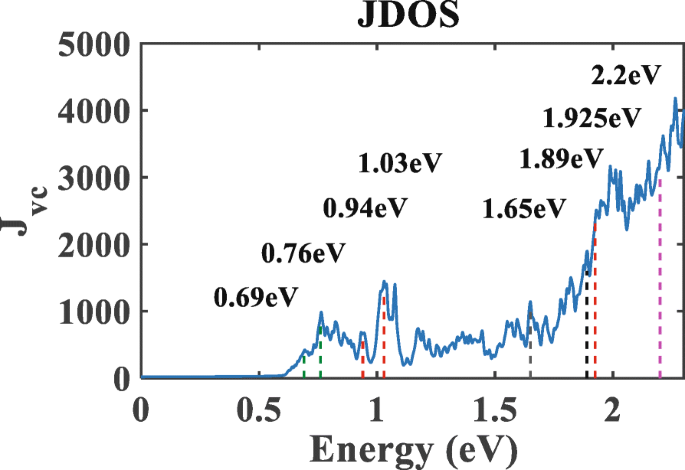
窒素ドープ単分子層MoS ₂ の結合状態密度 。点線はエネルギーの臨界点を示しています

図4と図3を対比すると、JDOSと光応答の間の密接な関係が示されます。そこでは、JDOSと光応答の両方が0.5 eV未満の光子エネルギーでほぼゼロになり、0.6〜1.7 eVの領域ではゼロではなくなりますが、小さいままです。その後、1.7〜2.3 eVの領域で大きく変動し、大きく変動します。特に、光子エネルギーが1.7 eVの場合、CPGEの光応答は顕著なピークを示します。図2bと組み合わせると、価電子帯から伝導帯への1.7 eVの光子エネルギーで励起される電子が制限されているため、不純物バンドを使用して電子が2つの遷移を持つ可能性があることがわかります。ただし、電子が価電子帯から不純物帯に移動し、次に不純物帯から伝導帯に移動する可能性があるため、光応答が最大振幅を持ちます。

光電流の振る舞いをさらに理解するために、次に、偏光角θの関数としてLPGEの光応答をプロットします。 [図5aを参照]。光応答の振幅は〜sin（2 θ）として動作することがわかります。 ）。これは、 C を持つ材料のLPGEの現象論的理論と一致しています。 _s 法線入射下での対称性、ここで\（{R_ {x}} {\ propto} E_ {0} ^ {2} {\ chi _ {xxy}} \ sin \ left（{2 \ theta} \ right）\）[ 21、26、54–56] E ₀ 光の電界強度とχ _xxy テンソルであること。興味深いことに、光応答関数はsin（2 θとして動作しますが ）光子エネルギーが2.0 eVの場合、代わりに− sin（2 θ ）光子エネルギーが2.1eVの場合。したがって、2.0eVと2.1eVの間に、光電流が消失する点、つまりLPGEのゼロ点が必然的に存在します。ゼロ点を特定するために、二分法に基づく方法を使用し、直線偏光のエネルギーに対する光応答の変化をプロットします。 θの図5bに示すように =π / 4度、2.012eVの光子エネルギーでゼロ点が発生します。式に従って先に指摘したように。 （12）、光電流はJDOSと運動量の行列要素の両方に依存します。 JDOSは計算で常に有限であることがわかっているため、ゼロ点の発生は電子遷移がないことにのみ起因する可能性があります。つまり、この場合のゼロ点の存在は禁制線によるものです。

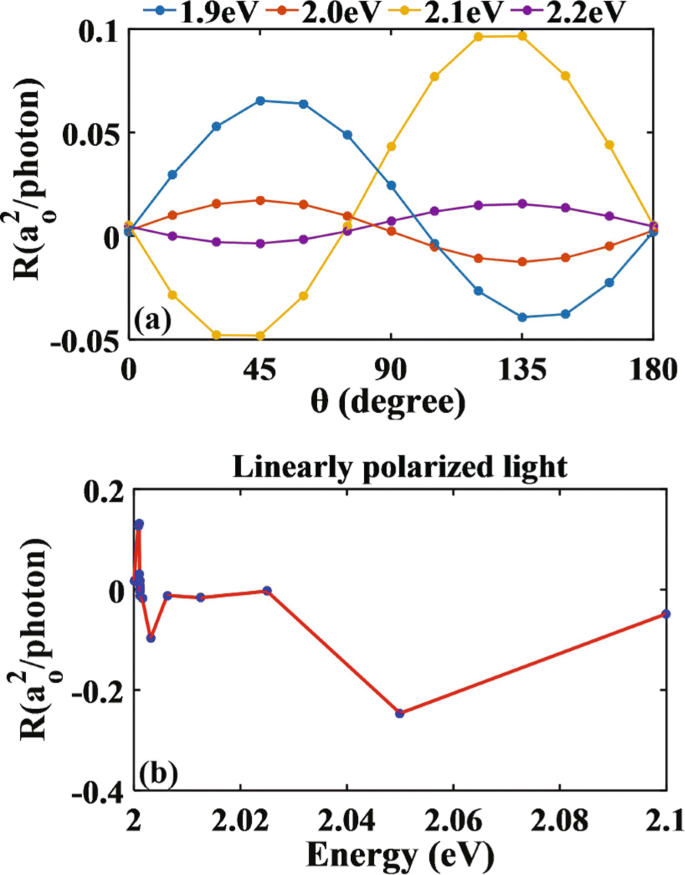
窒素ドープ単分子層MoS ₂ の光応答関数の振る舞い 直線偏光を垂直に照射します。 a による光応答関数のバリエーション 偏光角と b θの直線偏光のエネルギー =π / 4

比較のために、位相角 ϕ の関数としてのCPGEの光応答 図6に要約されています。 R が見つかります _x 〜sin（2 ϕ ）、再び\（{R_ {x}} {\ propto} E_ {0} ^ {2} {\ gamma _ {xz}} \ sin \ left（{2 \ phi} \右）\）γ _xz テンソルであること。 LPGEと同様に、CPGEもゼロ点を示します。これは図6bの2.2560eVで発生します。そこでは、遷移行列は常に有限であるため、LPGEの場合のように、このゼロ点を禁制遷移の観点から説明することはできません。代わりに、CPGEがRashbaSOCとDresslhausSOCの両方と深く関連しているという事実を呼び出します。これらはそれぞれ、異なる強度の価電子帯と伝導帯の分割に影響を与えます。 2つのバンドの分割が同一である特定のケースでは、伝導帯の励起された電子は、± k で反対の運動量を持ちます。 _x 。その結果、伝導帯の正味の電子電流はゼロになり、CPGEのゼロ点の存在を説明します。

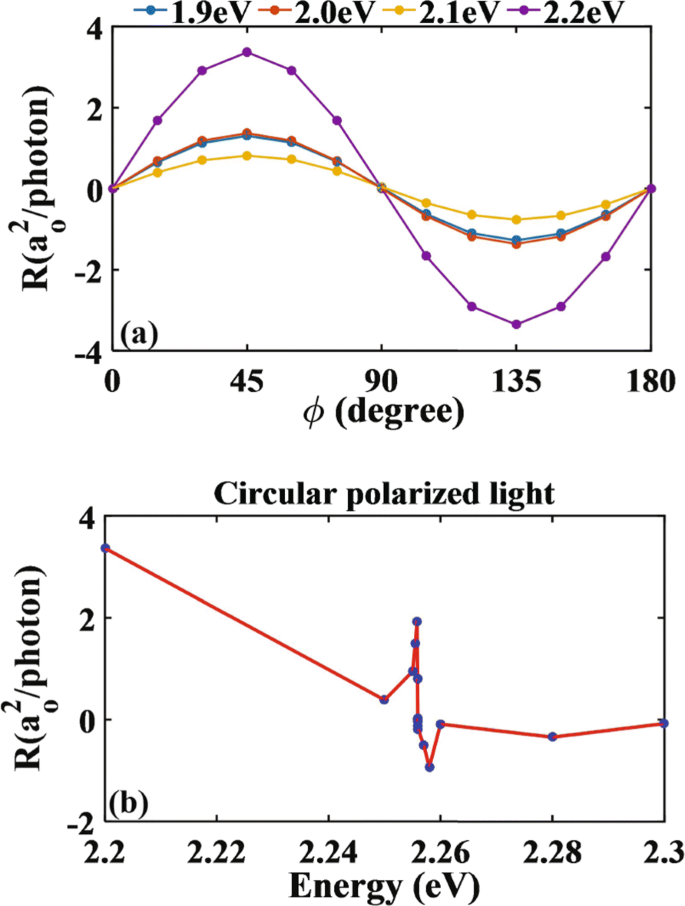
窒素ドープ単分子層MoS ₂ 楕円偏光が垂直に照射されます。 a 、 b ϕ の円偏光の位相角とエネルギーによる光応答関数の変化 =45 ^o 、それぞれ

興味深いことに、窒素をドープした単分子層MoS ₂ におけるCPGEの光応答 図1および2に示すように、LPGEよりも2桁強力です。 3、5、6。これは次のように理解できます。 LPGEの場合、光電流はキャリアの非対称散乱によって誘導されます。対照的に、CPGEは、材料が照射されると、伝導帯の電子がラシュバSOCとドレスルハウスSOCの下で不均衡な占有を示すために発生します。照射前は、窒素ドープ単分子層MoS _{2 <の空間逆対称性が壊れているためです。 / sub> 、元のサンプルのエネルギーバンドの縮退は、DresslhausSOCで解除されます。次に、材料が円偏光の照射を受けると、光子の角運動量がラシュバSOCによって電子のスピン角運動量に伝達されます。全体的な結果として、光学選択規則\（\ Delta {m_ {s}} =0、\ begin {array} {* {20} {c}} \ end {array} \ pm 1 \）を満たす電子は次のことができます。伝導帯に励起されます。これは、電子のスピン角運動量が線形偏光、つまりΔの下で不変のままであるLPGEとは異なります。 m s LPGEの場合は=0。したがって、ラシュバSOCとCPGEの\（\ Delta {m_ {s}} \ begin {array} {* {20} {c}} \ end {array} \ pm 1 \）により、電子の遷移確率はCPGEで劇的に増加し、より強力な光応答に貢献します。}

最後に、計算からわかるように、光子エネルギーは外部バイアスなしでシステム内で電気に変換され、可視光の吸収は窒素ドープ単分子層MoS ₂ で強力です。 特に、1.6〜2.3 eV [図3を参照]、つまり、赤色光から緑色光へ。したがって、2D光起電力デバイス[57]、rgb 1.00、0.00、0.00レーザー[58]、および単一光子エミッター[59]に適した材料です。さらに、光応答は、 R として与えられた光子エネルギーの偏光と位相角によって規則的に変化します。 〜sin（2 θ ）。したがって、偏光と位相角を制御して光電流を支配することが有用です。ただし、LPGEはわずかであるため、実験家は大きな光電流を得るために円偏光を使用する必要があります。さらに、バンド構造を持つJDOSの分析は、光電流の合理的な説明を提供し、光電子実験の結果の理論的基礎を提供します。

結論

要約すると、窒素をドープした単分子層MoS ₂ のPGEの第一原理研究を紹介しました。 NEGF-DFTに基づく垂直照射下。バンド構造と結合状態密度の分析を組み合わせて達成される光応答の振る舞いについて、満足のいく説明を提供します。 LPGEとCPGEの両方の光電流にゼロ点が存在することがわかりますが、根本的なメカニズムは異なります。 LPGEの場合、ゼロ点は2.0012 eVの光子エネルギーで発生し、価電子帯から伝導帯への電子励起に関連する遷移行列要素が消滅します。つまり、禁制遷移です。一方、CPGEの場合、光子エネルギーが2.2560 eVの場合、光電流はゼロになります。関連する遷移は常に許可されますが、ラシュバSOCとドレスルハウスSOCの両方が存在すると、正味のゼロ電流になります。さらに、窒素ドープ単分子層MoS ₂ におけるCPGEの光応答 LPGEより2桁強力です。一般に、光子エネルギー、偏光の種類、偏光角を変更して、2D光起電力デバイスの光電流を効果的に制御できます。現在の理論的研究は、ナノ材料の光ガルバニック効果の進行中の調査に光を当てる可能性があり、単層MoS ₂ を含むオプトエレクトロニクスおよび光起電アプリケーションへの新しい道を開くことができます。 。

データと資料の可用性

この調査中に生成または分析されたすべてのデータは、記事に含まれています。

略語

CPGE：

円形の光ガルバニック効果

LPGE：

線形光起電力効果

JDOS：

共同状態密度

GGA：

一般化された勾配近似

PBE：

Perdew-Burke-Ernzerhof

DZP：

ダブルゼータ偏光

DFT：

密度汎関数理論

NEGF：

非平衡グリーン関数法