ナノインデンテーションを介した材料の転位の進展と機械的性質に及ぼす機械加工によって誘発された表面下欠陥の影響

背景

ナノメートルスケールでの超精密製造は、サブミクロンの寸法精度とナノスケールの表面品質を備えたナノコンポーネントを取得するための効果的な方法であると広く考えられています[1]。製造後、ワークピースの内部に安定した表面下の欠陥がいくつか残っています[2、3、4、5]。表面下の欠陥は、処理精度と表面品質に影響を与えるだけでなく、ナノコンポーネントの機械的特性と耐用年数にも重大な影響を及ぼします。表面下欠陥に関する多くの研究は、分子動力学（MD）法によって行われ、主に表面下欠陥s [6、7]、表面下欠陥（SSD）層の厚さ[8、9]、および表面の完全性に対する表面下の欠陥の影響[10、11]。ただし、ワークピース材料の機械的特性に及ぼす表面下欠陥の影響はあまり研究されていません。ナノ構造の機械的特性は、そのサービス性能と寿命にとって重要です。したがって、材料の機械的特性に対する表面下の欠陥の影響は、調査すべき重要な問題になっています。

ナノカッティングプロセスの分子動力学シミュレーションによってSSD層を検討するために多くの研究が行われてきました。 Narayanan [12]は、単結晶金における積層欠陥四面体（SFT）の形成を研究し、SFTの変形誘起メカニズムを導入しました。稲村[13]は、ナノカッティングプロセス中の切りくず形成と材料すべり変形を調査し、切りくず形成は主にせん断すべり変形によって引き起こされることを指摘しました。 Pei [14]は、転位の進展とナノ切削プロセス中に強制される切削に対する切削パラメータの影響を研究し、ワークピースが40 nmより大きい場合、サイズの影響は重要ではないことを発見しました。 Dai [15]とLiu [16]は、それぞれMDシミュレーションと実験方法を採用して、ワークピースの表面下欠陥の進展に対するダイヤモンド工具の構造とサイズの影響を研究しました。以前の研究は、ナノ切削後のワークピースに安定した表面下欠陥が存在することを示しています。切削パラメータと工具形状パラメータは、表面下の損傷層の厚さと進展、さらには加工精度にも大きな影響を及ぼします。ただし、ナノカッティングで得られた関連データを分析して、被削材の機械的性質を計算することはできません。

ナノインデンテーションは、硬度や弾性率などの機械的特性を特徴付ける効果的な手法です[17]。実験的および理論的モデルによって機械的特性の性能を評価するために、ナノインデンテーションに関する多くの研究が行われてきました。 Zimmerman [18]は、すべりベクトルによるナノインデンテーションプロセスでの転位放出を分析しました。 Ruestes [19]は、MDシミュレーションによって単結晶Feのナノインデンテーションを研究し、インデンテーションゾーンから材料を除去するために表面下での転位生成が必要であることを発見しました。 Huang [20]は、単結晶ダイヤモンドマトリックス上でナノインデンテーションのMDシミュレーションを実行し、インデンテーション下のダイヤモンド材料の変形は、<110> {111}転位ループの核形成と伝播によって支配されることを発見しました。 Sharma [21]は、銅マトリックスで人工的に硬質粒子モデルを構築し、機械加工プロセスにおける表面下の欠陥の進展に対する硬質粒子の影響を分析しました。 Peng [22]は、ナノインデンテーションによるCu基板上のグラフェンコーティングの強化メカニズムを調査しました。これは、界面によって生成される応力均質化効果に起因します。上記の分析から、表面下欠陥の影響に関するこれまでの研究は、主に完全結晶材料または実際の表面下欠陥から遠く離れた人工的な構築仮想欠陥に基づいていることがわかります。したがって、表面下の欠陥がワークピースの機械的特性に与える影響を分析するには、表面下の欠陥を含むワークピースモデルを現実的に構築することが不可欠です。

本論文では、ナノカッティング法を採用して、実用的な特性に一致する表面下欠陥を有するワークピースモデルを得た。これに基づいて、ナノインデンテーションシミュレーションを実行して、単結晶銅の機械的特性に対する表面下の欠陥の影響を研究しました。まず、ナノカッティングプロセス中の表面下欠陥の形成と進展のメカニズムについて説明し、ナノカッティング後のワークピースの表面下の典型的な欠陥構造を分析します。第二に、機械加工によって誘発された表面下欠陥と圧痕中の転位核形成との間の相互作用メカニズムを分析します。第三に、ナノインデンテーションによって得られた荷重-変位データに基づいて、単結晶銅試料の硬度とヤング率が計算されます。最後に、いくつかの新しい結論を要約します。

メソッド

シミュレーションモデル

ナノマシニングにおける材料の機械的特性に対する表面下欠陥の影響を調査するために、表面下欠陥のある試験片モデルを構築する必要があります。本研究では、ナノカッティングプロセスのMDシミュレーションにより実現しました。まず、MDシミュレーションモデルを確立し、ナノカッティングプロセスシミュレーションを実行します。 次に、MDシミュレーション中に試験片と切削工具を十分な時間リラックスさせます 。最後に、いくつかの安定した欠陥が地下に残っていました ワークピースの。三次元MDシミュレーションモデルの概略図を図1に示します。ここで、ナノカッティングモデルを図1aに示し、表面下欠陥のあるナノインデンテーションモデルを図1bに示します。図1では、ワークピースと試験片の材料は単結晶銅であり、工具と圧子はダイヤモンド材料です。アークブレードダイヤモンド工具はナノカッティングプロセスで使用され、工具のエッジ半径は3nmです。圧子はナノインデンテーションプロセスで半球形であり、直径は6nmです。ワークピースと試験片は、それぞれニュートン層、温度層、境界層の3つの部分に分かれています。サイズ効果と境界効果を低減するために、シミュレーションシステムの[010]方向に周期境界条件（PBC）が採用されています。ツールとワークピース間の最初の相互作用を回避するために、切削ツールはワークピースの右上3 nmに配置され、圧子は試験片の6nm上に配置されます。詳細なシミュレーションパラメータを表1に示します。

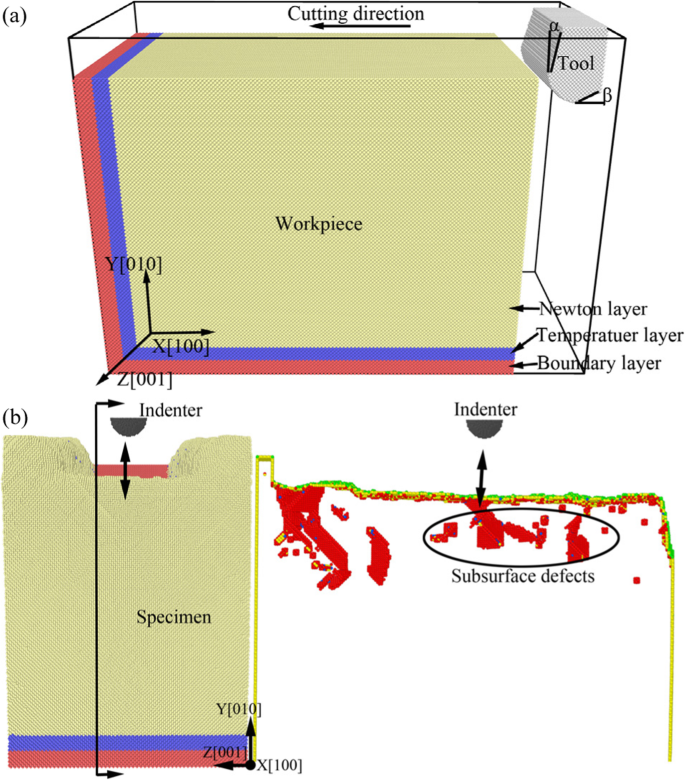
ナノカッティングおよびナノインデンテーション用の単結晶銅の3DMDシミュレーションモデルの概略図。 a ナノカッティングプロセスのモデル。 b 表面下の欠陥を伴うナノインデンテーションプロセスのモデル

原子間ポテンシャル関数

この研究では、3次元MDシミュレーションは、大規模な原子/分子の大規模並列シミュレーター（LAMMPS）によって実行されました。並列計算は、メッセージパッシングインターフェイスライブラリの助けを借りて実現されました。シミュレーションでは、LAMMPSソフトウェアパッケージから呼び出されるモースポテンシャル、EAM（Embedded-atom Method）ポテンシャル、およびTersoffポテンシャルが使用されます。ワークピース内のCu原子とツール内のC原子の間の相互作用は、式（1）に示されているモースポテンシャルによって計算されます。 1 [23]。

ここで r ₀ 、α 、および D それぞれ、原子間隔、弾性率、および結合エネルギーです。値を表2に示します。

ワークピース内のCu原子間の原子間関数は、式（1）に示されているEAMポテンシャルによって記述されます。 2、3 [24、25]。

ダイヤモンドツール内の炭素原子間の相互作用は、式（1）に示されているTersoffポテンシャルによって計算されます。 4、5 [26]。

ここで f _c （ r _ij ）は原子間の切り捨て関数、 V _A （ r _ij ）は吸収項の二重ポテンシャル V _R （ r _ij ）は反発項の二重ポテンシャルであり、 r _ij は原子間の原子距離 i およびアトム j 。

欠陥分析方法

単結晶銅のナノカッティングでは、ワークの表面下で変形や転位が発生します。この論文では、中心対称パラメータ（CSP）を導入して、ワークピースの転位核形成と欠陥進展を分析します。面心立方（FCC）材料の場合、CSP値は式（1）で計算できます。 6 [27]。

ここで R _i は同じ長さの隣接する原子であり、 R _{i + 6} 反対方向の隣接原子です。 FCC結晶、部分転位、積層欠陥、および表面原子のCSP値は、それぞれ0、2.1、8.3、および24.9です[27]。

CSP法では、千鳥状の原子を特定することはできますが、ワークピースの局所的な原子結晶構造の状態を認識することはできません。したがって、局所的な結晶構造の欠陥を特定するために、Common Neighbor Analysis（CNA）が導入されています。 Honeycutt and Andersen [28]によって提案された元のCNA法では、さまざまな構造が図で表されます。現在、OVITOには5種類のCNAパターンがあり[29]、局所的な結晶構造は面心立方（FCC）、最密六角形（HCP）、体心立方（BCC）、イコソヘドラル（ICO）、それぞれ不明。この論文では、転位抽出アルゴリズム（DXA）[30]も、転位欠陥の進展を分析するために導入されています。 DXAにより、ワークピースのさまざまな結晶構造がさまざまな色でマークされ、ワー​​クピースの転位欠陥がさまざまな色の線で表されます。

結果と考察

ナノ切削プロセスにおける表面下の欠陥の進展

ナノカッティング工程では、切削工具のワークへの押し出し・せん断作用により、切削深さの厚みのあるワーク表面材を除去し、一定のサイズ精度と表面品質を備えた新たな加工面を形成します。エネルギー変換と応力集中に伴い、ワークの表面と表面下に応力変形と熱変形を含む複雑な弾塑性変形が発生します。したがって、表面下の損傷層が形成され、チップが除去されます。図2は、単結晶銅のナノカッティングプロセス中の表面下の欠陥の進展と材料の除去の瞬間図を示しています。図2では、CSPおよびCNAの分析結果の値によって原子が色分けされています。図2aおよびcでは、黄色、緑色、赤色、および青色の原子は、表面原子、表面欠陥原子、表面下欠陥原子、およびFCC原子です。図2から、ナノカッティングプロセス中に、点欠陥、空孔欠陥、積層欠陥、クラスター欠陥、角柱状転位、らせん転位ループなど、多くの典型的な欠陥構造がワークピースの表面下に形成されることがわかります。

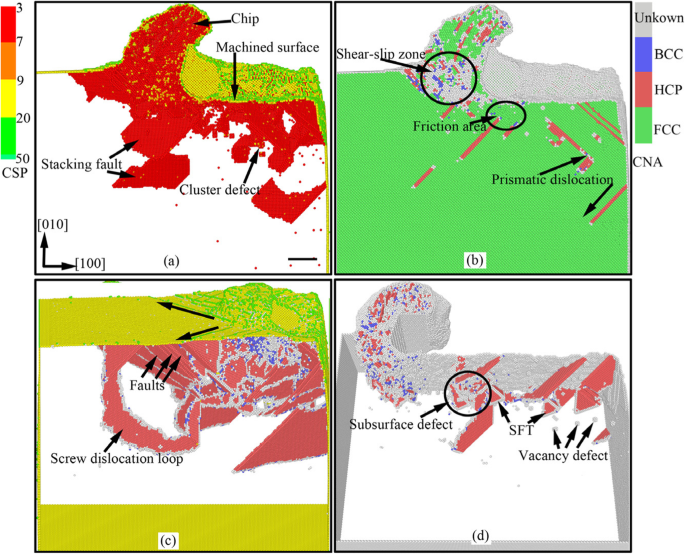
単結晶銅のナノカッティングプロセス中の表面下欠陥の進展のインスタントビュー（オンラインカラー、スケールバー5 nm）。 a の切断距離 、 b 、 c 、および d それぞれ18nm、18 nm、6 nm、32 nm

切削工具の圧搾とせん断効果により、すくい面の前の原子にせん断すべり変形が発生し、図に示すように、ナノ切断プロセス中にワークピースに一次せん断すべりゾーンが形成されます。 。2b。これらの原子の一部はすくい面に沿って滑り上がり、図2aに示すようにカッティングチップが形成されます。図2bに示すように、一部が下向きに移動し、工具側面の圧搾摩擦によって加工面が形成されます。他のものは内側に移動し、図2aおよびbに示すように、積層欠陥、クラスター欠陥、および角柱状転位などの表面下欠陥が形成されます。

工具逃げ面の摩擦と押し出しにより、逃げ面付近の原子にエネルギーが蓄積し、高エネルギー原子になります。原子エネルギーが一定のレベルを超えると、高エネルギー原子によって運ばれたエネルギーが放出され、高エネルギー原子が駆動する下で転位が形成されます。そのため、図2dに示すように、側面摩擦領域に多くの転位が形成されます。機械加工された表面が形成されると、転位は表面下で核形成、伸長、および消滅します。最後に、図2dに示すように、積層欠陥、SFT、空孔欠陥などの欠陥構造が地下に残されます。積層欠陥は、切削工具の下のせん断滑りゾーンで核形成され、次にワークピース内に拡張され、最後にワークピースの自由表面で消滅します。最終的に、転位線がワークピース表面に形成されます。そして、転位線は\（\ left [\ overline {1} 0 \ overline {1} \ right] \）、\（\ left [\ overline {1} 01 \ right] \）、および[101]に沿って延長されます。方向。せん断すべり帯の端に位置するらせん転位ループは、いくつかの積層欠陥と一連のらせん転位で構成されています。螺旋転位は、せん断すべり帯の圧縮応力状態の駆動下で形成されます[11]。

ナノカッティングプロセスでは、転位は、カッティングツールの作用下で核形成および伸長されます。エネルギーの凝集と放出に伴い、切削距離の増加に伴って切削抵抗が変動します。これを図3に3次元で示します。図3では、黒、赤、青の曲線はそれぞれ、送り力（Fx）、逆力（Fy）、接線力（Fz）です。図3から、切断工程は初期切断段階と安定切断段階の2つの期間に分かれていることがわかります。初期切削段階では、送り力と後力が直線的に急激に増加します。送り力の最大値は1100nNを超えていますが、逆力は600nN付近に到達しています。ツールチップがワークピースに完全に切り込むと、図3に加工面として署名された最初の小さなグラフとして示される加工面が形成されます。次に、ナノ切削プロセスが安定した切削段階に移行します。安定した切削段階では、3つの力すべてが平衡位置で変動しています。平均送り力は約1000nNで、平均逆力は約500nNです。図3から、切削距離20nmで送り力が急激に低下していることがわかります。これは、図3の2番目の小さなグラフに示すように、エネルギーの蓄積が臨界格子ひずみエネルギーである特定のレベルに到達するためです。その間、切削工具に大きな抵抗が作用し、切削力がピーク値。その後、エネルギーが放出されて転位が放出され、切削抵抗が減少します（図3の3番目の小さなグラフ）。したがって、安定した切削段階では切削抵抗が変動します。転位の核形成、伸長、消滅により切削抵抗が変動し、最終的にはワークに表面下欠陥が存在します。

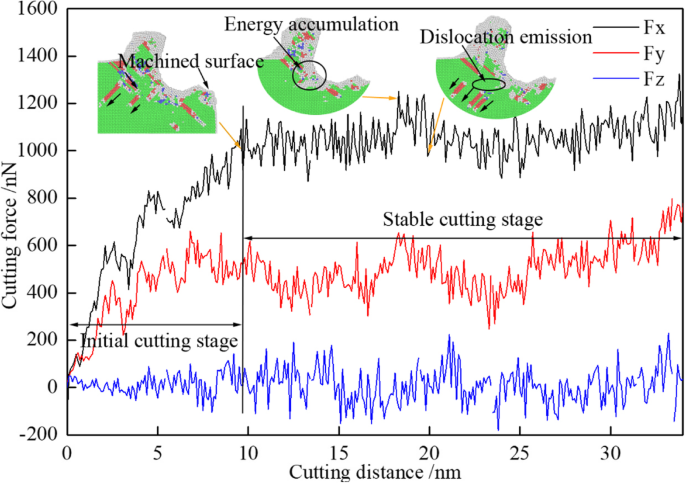
切削距離による切削抵抗の変化曲線（オンラインカラー）。黒、赤、青の曲線はそれぞれ、送り力（Fx）、逆力（Fy）、接線力（Fz）です。

ナノカッティングプロセス中のワークピースの表面下の転位欠陥の進展と感情を詳細に調査するために、転位分布とそのカッティング距離による変化をCNA法によって詳細に分析します。図4a、b、c、d、e、fの切削距離がそれぞれ8 nm、10 nm、12 nm、20 nmである、特定の領域でのワークピースの表面下欠陥の進展を図4に示します。 、24 nm、および32nm。図4aから、切削工程の予備段階での切削工具の押し出しせん断作用により、せん断すべり帯に多くの転位欠陥が発生していることがわかります。特に、図4bに示すように、せん断すべり帯では、原子応力とエネルギーの駆動作用により、V字型の転位と断層が形成されます。後続の処理プロセスでは、せん断スリップゾーンが前方に移動し、切削工具が動き続けます。変形エネルギーが減少するため、断層は徐々に消滅します。切削工具が前進し続ける間、逃げ面摩擦ゾーンは断層の近くに移動します。そして、粗加工面は逃げ面の押し出しと摩擦の下に形成されます。次に、図4dに示すように、障害は消滅し続け、ワークピースの表面から徐々に切り離されます。最後に、断層は、ワークピースの地下に着実に存在するクラスター欠陥に変換されます。同様に、形成されたV字型転位は、2つの積層欠陥と転位ロックの相互作用の下で徐々にSFTに進化します。これらの安定した欠陥は、図4eおよび図4fに示すように、表面下の変形層で構成されています。

ワークピースの表面下欠陥の進展（オンラインカラー）。 a の切断距離 、 b 、 c 、 d 、 e 、および f それぞれ8nm、10 nm、12 nm、20 nm、24 nm、32 nm

ご存知のように、残留応力の解放と内部欠陥の回復が発生します 時効処理後のワークに。実際のナノファブリケーションでは、加工中に形成された表面下の欠陥の一部は、機械加工プロセス後に消失します。時効処理後のワークの状態をシミュレートするために、分子動力学緩和が切断システムで長時間実行されます。長時間のMD緩和後のワークの表面下の残留欠陥の分布図を図5に示します。ここでは、CSPおよびCNA法による分析結果に従って原子が着色されています。図5から、緩和後に一次転位が消滅していることがわかります。図5に示すように、空孔欠陥、積層欠陥、原子クラスター、角柱転位、らせん転位、SFT、および階段状転位がワークピースの表面下に存在します。上記の分析によると、これらの欠陥は複雑な内部応力の誘導と転位欠陥の相互作用は、ナノ処理後のワークピースのサイズ精度と表面品質に影響を与えます。

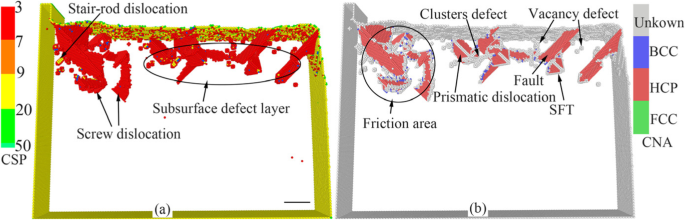
ナノメートル切断後のワークピースの表面下の残留欠陥の分布（オンラインカラー、スケールバー5 nm）。 a 黄色、緑色、赤色、青色の原子は、表面原子、表面欠陥原子、表面下欠陥原子、およびFCC原子です。 b 緑、赤、灰色、および青の原子は、FCC、HCP、不明、およびBCC構造です

機械加工によって誘発された表面下の欠陥がある銅試験片のナノインデンテーションテスト

機械加工によって引き起こされる表面下の残留欠陥は、表面の機械的特性、特に硬度とヤング率を左右します。したがって、ナノインデンテーション中の転位の核形成と相互作用の調査が強く必要であるように思われます。単結晶銅の機械的性質に及ぼす機械加工による表面下欠陥の影響を調査するために、ナノカッティングシミュレーションと同じパラメータを使用して、ナノカッティング後の試験片のナノインデンテーションプロセスを実施しました。シミュレーション結果を図1、2に示します。 6、7、8、9、10。ナノインデンテーションの初期状態での表面下欠陥分布の瞬間原子像を図6に示します。この図から、V字型のSFTがいくつかあることがわかります。転位、いくつかの角柱状転位、および圧子の下のいくつかのクラスター欠陥。これらの表面下の欠陥は、ナノインデンテーションプロセス中のワークピースの転位核形成と膨張に影響を与える可能性があります。そして、被削材の機械的性質が変化します。

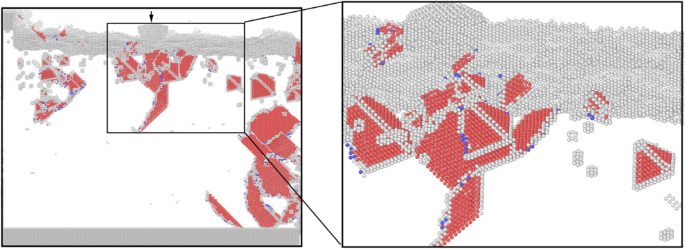
初期押し込み状態（オンラインカラー）でのワークピースの表面下欠陥分布。赤、灰色、および青の原子は、HCP、不明、およびBCC構造です

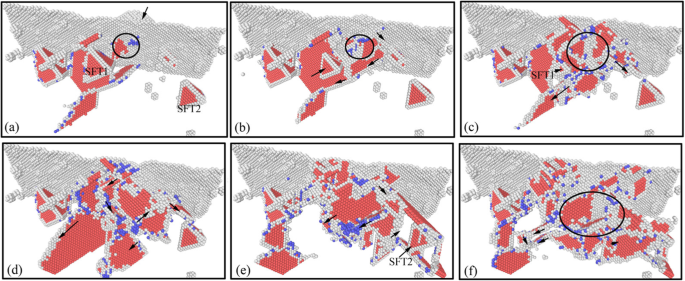
ナノインデンテーションのローディングプロセスにおける表面下転位欠陥の進展（オンラインカラー）。 a の対応するインデントの深さ – f それぞれ0nm、0.5 nm、1 nm、2 nm、3 nm、4nmです

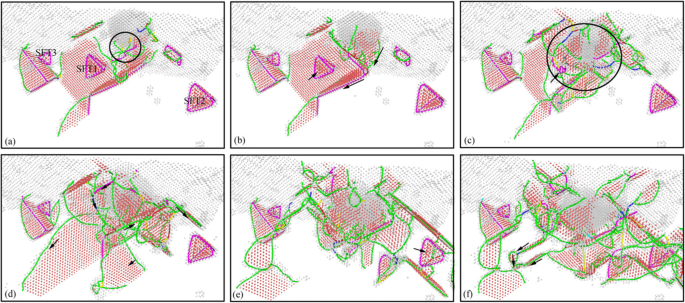
ナノインデンテーションのローディングプロセスにおける地下転位の分布（オンラインカラー）。 a の対応するインデントの深さ – f それぞれ0nm、0.5 nm、1 nm、2 nm、3 nm、4nmです。配色：完全な転位の場合は濃い青、ショックリー転位の場合は緑、ステアロッド転位の場合はピンク、ハース転位の場合は黄色、フランク転位の場合は水色、未確認の転位の場合は赤

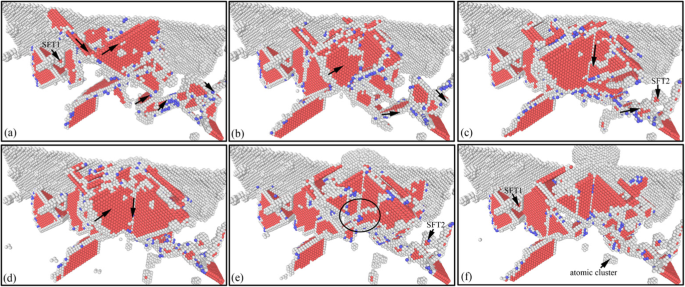
ナノインデンテーションのアンロードプロセスにおける表面下欠陥の進展（オンラインカラー）。 a の対応するインデントの深さ –fは、それぞれ4 nm、3 nm、2 nm、1 nm、0 nm、および-1nmです

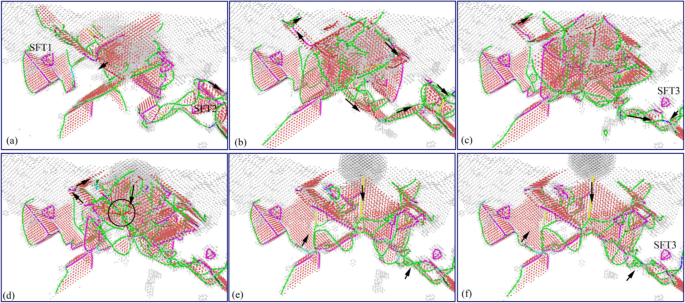
ナノインデンテーションのアンロードプロセスにおける地下転位の分布（オンラインカラー）。 a の対応するインデントの深さ – f それぞれ4nm、3 nm、2 nm、1 nm、0 nm、および-1nmです。配色：完全な転位の場合は濃い青、ショックリー転位の場合は緑、ステアロッド転位の場合はピンク、ハース転位の場合は黄色、フランク転位の場合は水色、未確認の転位の場合は赤

ナノインデンテーションローディングプロセス中の表面下転位の原子進化画像を図7に示します。図7aから、圧子が試料の表面に接触すると、転位の初期核形成が試料の表面で発生することがわかります。検体。圧子の下向きの圧力で、有核転位は徐々に膨張します。一方、圧子による応力の影響下で、図7bに示すように、多数の転位が核形成し、スリップシステムに沿って移動しました。新たに形成された転位と元の表面下の欠陥との相互作用の下で、いくつかの単純な欠陥は徐々に消え、V字型の転位は徐々に進化し、消滅し続けます。図7cに示すように、圧子の下のSFTは徐々に減少します。圧痕プロセスが進むにつれて、新しい有核転位欠陥の規模が大きくなり、圧子の下のV字型転位とSFT1が徐々に消えます。同時に、押し込み中に形成された転位欠陥は、図7dに示すように、積層欠陥が徐々に消える角柱状転位ループに徐々に進化します。新しく形成された角柱状転位ループは、圧子の右下にあるSFT2まで伸び続けています。その安定した構造のために、SFT2は、図7eに示すように、角柱状転位ループの拡張中に変形しないままです。圧子が押し下げられると、角柱状転位ループは下向きに拡大し続け、地下領域の転位欠陥の規模は徐々に大きくなります。図7fに示すように、SFT2構造は試料の表面下に安定して存在し、転位欠陥の移動や干渉の際に変化はありません。

圧痕プロセス中の表面下欠陥の進展と分布をより明確に示すために、DXA法を使用して圧痕後の試験片を分析します。図7に対応する各時間の地下転位分布の画像は、図8に示すようにDXA分析によって得られます。転位は次のスキームに基づいて色付けされます：完全な転位の場合は濃い青、ショックリー転位の場合は緑、ステアロッドの場合はピンク転位、Hirth転位の場合は黄色、Frank転位の場合は水色、未確認の転位の場合は赤。

図8から、ワークの表面下は主にショックリー転位と初期くぼみ状態のステアロッド転位で構成されていることがわかります。地下に存在するSFTは、6つの階段状転位からなる規則的な四面体構造です。圧子がワークピースに接触すると、図8aに示すように、ワークピース表面の転位核生成は黄色のハーシュ転位になります。圧子が押し下げられると、多数の転位が核形成され、スリップシステムに沿って移動します。図8bに示すように、黄色のHirsh転位は徐々に緑色のShockley転位に変化します。図8cに示すように、新しく形成された転位と元のSFT1との相互作用の下で、いくつかの単純な転位が徐々に消えていきます。圧子が落下するにつれて地下転位の規模が大きくなり、新しく形成された転位は主に緑色のシャックリー転位です。図8dに示すように、Shockley転位とSFT1の間の相互作用により、SFT1のサイズが徐々に減少し、最終的にSFT1が消失します。欠陥のスケールが大きくなると、試料の表面下の転位の数と種類が増えます。図8eに示すように、表面下に形成された赤い未知のタイプの転位があり、いくつかのショックリー転位がプリズム転位ループを構成していました。ショックリー転位とステアロッド転位の相互作用の下で、図8fに示すように、圧子の押し出しが弱いため、圧痕領域から遠く離れたSFT2とSFT3は最終的に消えませんでした。

ナノインデンテーションアンロードプロセス中の表面下転位の進展画像を図9に示します。図10は、図9に対応する表面下転位の分布画像を示しています。2つのグラフから、表面下欠陥のスケールが増加していることがわかります。最初は、圧子が上に移動する過程で徐々に減少します。これは、材料の変形エネルギーの連続放出と圧子が試験片に及ぼす付着力との間の包括的な機能によって引き起こされます。除荷プロセスの初期段階では、圧子が試料に及ぼす上向きの吸着力は重要ではありません。表面下欠陥の進展は、主に材料の変形エネルギーによって引き起こされ、その結果、表面下欠陥の規模が大きくなります。そして、ステージ内の転位の主なタイプは、図1および2に示すように、緑色のショックリー転位とピンクのはしご転位です。 9a、bおよび10a、b。 SFT2と近くのShockley転位との相互作用により、ピンク色の階段状転位が、圧子作用から遠く離れた領域で緑色のShackley転位に変わります。 Meanwhile, the SFT2 is transformed into a smaller defect which is SFT3, as shown in Figs. 9c and 10c. With the continuous lifting of the indenter, the bonding and adsorbing effect exerted by the indenter on the specimen increases gradually. Accompany with the deformation energy release, the size and types of dislocations in subsurface increase. And more perfect dislocations, Hirh dislocations, and unknown dislocations are formed, as shown in Figs. 9d and 10d. In later stage of unloading process, the material deformation energy is basically released, and the evolution of subsurface defects is dominated by the adsorption from the indenter. Therefore, the subsurface defects are annihilated rapidly, and the scale of subsurface defects decreases rapidly. And a typical Hirsch dislocation is formed in the direction of the indenter upward, which is shown in Figs. 9e, f and 10e, f. Finally, the scale of subsurface defects decreases considerably, and some typical subsurface defects, such as SFT and atomic clusters, are gradually disappeared. From the above analysis, it can be seen that secondary processing (nano-indentation) can restore the typical internal defects formed in nano-cutting, and the subsurface damage becomes more serious in the secondary processing area. These characteristics of subsurface defects will affect the mechanical properties of materials. Hence, it is necessary to study the effect of subsurface defects on the mechanical properties of material.

Mechanical properties of materials can be calculated by load-displacement curve, such as hardness, elastic modulus, and yield strength. In this study, hardness and Young’s modulus of single crystal copper were investigated. The variation of load on the indenter was monitored during the nano-indentation process, and the load-displacement curve of the nano-indentation process was drawn, as shown in Fig. 11. The max indentation depth of the red and black curves respectively is 2 nm and 3 nm, in which both loading and unloading processes are included. The upward direction of load is defined as positive direction, so the load-displacement curves are all above the zero line in the process of loading, while the load on the indenter changes from positive to negative during unloading. The elasticity restore of deformed matrix material exerts an upward force on the indenter. Therefore, in order to keep the indenter raising in uniform speed, a downward force (positive) is required. With the gradual recovery of deformation, the force gradually decreases until it disappears. Then the force applied on the indenter becomes negative, and the absolute value of the force first increases and then decreases. From the graph, it can be seen that the specimen is in the stage of elastic deformation during loading process, and the load increases in proportion to the displacement. When the displacement of the indenter is 1 nm, the load on the indenter is fluctuated dramatically, as indicated by the arrow on the left side of Fig. 11. This is because that the indenter is pressed down to the SFT1 shown in Fig. 7, which results in the greater impediment to the indenter. When the indenter displacement is in the range of 2 to 3 nm, the fluctuation amplitude of the load increases. This is because the indenter is pressed down to the SSD layer, and the impediment of the indenter to the subsurface defect in the specimen is more significant, so the fluctuation amplitude of the load increases significantly.

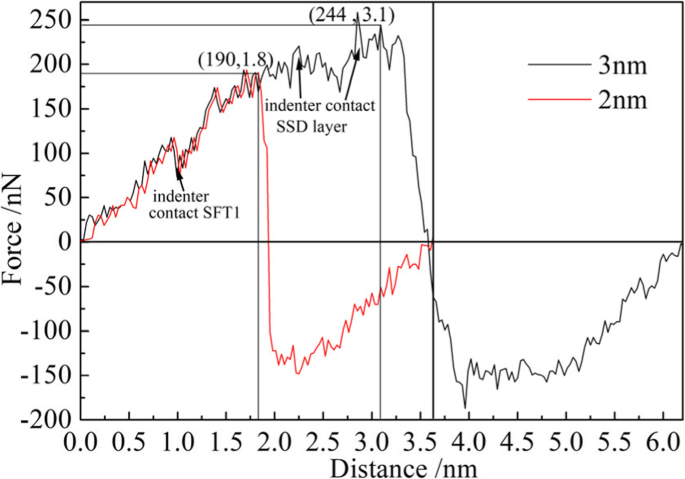
Load-displacement curve of nano-indentation on the machining-induced specimen (color online). The maximum indentation depth of the black curve and the red curve respectively is 3 nm and 2 nm

According to Oliver-Pharr Method [31], nano-indentation hardness can be defined as indentation load divided by the contact area between indenter and specimen, which is calculated by Eq. 7.

In which, F _max is the peak value of the load. A _c is projected contact area for indenter and specimen, which can be obtained by

ここで r is contact radius for indenter. Because the indenter is hemispherical in shape, r is approximately equal to indentation depth.

The elastic deformation of single crystal copper material is caused by the load exerted from indenter. Based on the previous load-displacement curve, Young’s modulus (E ) of single crystal copper can be calculated by Eq. 9.

ここで F is applied load, S is contact area, r is projection radius of indenter, DL is material deformation along loading direction, which is equal to indentation depth, and L is the total length of material along loading direction. In this study, L is equal to 30 nm.

According to the Oliver-Pharr method and load-displacement data, nano-indentation hardness and Young’s elastic modulus of single crystal copper materials with subsurface defects can be calculated based on Eqs. 7, 8, 9. Table 3 shows the applied load acting on the specimens by indenter with different indentation depths.

The nano-indentation hardness of single crystal copper can be calculated by Eqs. 7 and 8 combining the data in Table 3. When the maximum depth is 2 nm, F _max =190.67 nN and from Fig. 11 r =2.75 nm. The calculated value of nano-indentation hardness H2 is 8.029 GPa. When the maximum depth is 3 nm, F _max =244.66 nN and r =3 nm. The calculated value of nano-indentation hardness H3 is 8.675 GPa, which is slightly larger than it obtained at indentation depth of 2 nm. It is because the indenter is pressed down to the subsurface defects area at indentation depth of 3 nm, and the deformation resistance of the subsurface defects increases. Therefore, the hardness of the single crystal copper increased. It can be concluded from the result that the subsurface defects make the machined surface much harder, which is work-hardening phenomenon.

The Young’s modulus E of single crystal copper can be calculated by Eq. 9 combining the data in the Table 3. The calculation results are shown in Table 4. It can be noted that the Young’s modulus becomes distinctly higher when the indentation depth is smaller than 1.5 nm. In the initial stage of nano-indentation, the indenter does not contact the defects residual area in subsurface. However, the work-hardening effect makes the specimen material not easily be occurred elastic deformation; therefore, the Young’s modulus of single crystal copper is larger in the initial stage of indentation. The value of Young’s modulus is 119.4 GPa when indentation depth is 2 nm, which is almost the same with Zhang’s research (120.4 GPa) [14]. With the increase of indentation depth, the Young’s elastic modulus of single crystal copper specimens decreases gradually, and the ability of materials to resist elastic deformation is weakened. It is due to the permanent elastic deformation is derived from the dislocation motion and its interaction with subsurface defects. It has been revealed that the nano-cutting-induced subsurface defects will affect the physical and mechanical properties of single crystal copper materials, which is also applicable to other FCC materials. The existence of subsurface defects will enhance the hardness of machined surface and weaken the ability of material to resist elastic deformation, in which the mutual evolution between dislocations and subsurface defects plays an important role. Therefore, it is very important to predict the thickness of subsurface deformation layer and study the surface properties for nano-fabrication.

結論

The subsurface defects stable exist in workpiece after nano-cutting can affect the mechanical properties, which is critical to the service performance and life of nano-structures. The previous studies are mainly based on perfect crystal materials or artificial constructing hypothetical defects, which is far from the actual subsurface defects. In this paper, molecular dynamics simulation of nano-cutting is performed to construct the specimen model with subsurface defects. Based on the built MD model, nano-indentation simulation is carried out to study the influence of machining-induced subsurface defects on the physical and mechanical properties of single crystal copper materials. The interaction mechanism between dislocation and complex defects during nano-indentation is studied. The nano-indentation hardness and Young’s elastic modulus of single crystal copper materials are calculated. Based on the above analysis, some interesting conclusions can be drawn as follows.

1. 1.

   The dislocation nucleation and expansion in workpiece subsurface are driven by the extrusion and shearing action of cutting tool during the nano-cutting process, which results in the fluctuation of cutting force. After nano-cutting, there are stable defect structure residues in the subsurface of workpiece, such as vacancy defects, stacking faults, atomic clusters, SFT, and stair-rod dislocations, which together constitute the subsurface defect layer of workpiece.

2. 2.

   The existence of subsurface defects affects the nucleation and expansion of dislocations during nano-indentation process. Some stable defects directly below the indenter, such as V-shaped dislocation and SFT1, are annihilated after indentation. And SFT2 far from the indentation region is transformed into a smaller one. Secondary processing of nano-indentation can restore typical internal defects of the workpiece, but the subsurface defects in the secondary processing area are aggravated.

3. 3.

   The nano-indentation hardness of specimens increases with the introduction of subsurface defects, which results in the formation of work-hardening effect. The Young’s modulus of single crystal copper is larger in the initial stage of indentation and gradually decreases with the increase of indentation depth. The existence of subsurface defects can weaken the ability of material to resist elastic deformation, in which the mutual evolution between dislocations and subsurface defects plays an important role.

データと資料の可用性

この原稿でなされた結論は、この論文で提示され示されているすべてのデータに基づいています。

略語

MD：

分子動力学

SSD：

Subsurface defects

SFT:

Stacking fault tetrahedral

PBC：

周期境界条件

LAMMPS:

Large-scale atomic/molecular massively parallel simulator

EAM：

埋め込み原子法

CSP：

中心対称性パラメーター

FCC：

面心立方

CNA：

一般的なネイバー分析

HCP：

密集した六角形

BCC：

体心立方

ICO：

Icosohedral

DXA：

転位抽出アルゴリズム