隠れ層ニューラルネットワークの精度を上げる方法

この記事では、いくつかの分類実験を実行し、隠れ層の次元とネットワークパフォーマンスの関係に関するデータを収集します。

この記事では、Pythonの実装と問題の例を使用して、ニューラルネットワークの精度を向上させるために隠れ層を変更する方法を学習します。

ただし、そのテーマに移る前に、ニューラルネットワークに関するこのシリーズの以前のエントリに追いつくことを検討してください。

1. ニューラルネットワークを使用して分類を実行する方法：パーセプトロンとは何ですか？
2. 単純なパーセプトロンニューラルネットワークの例を使用してデータを分類する方法
3. 基本的なパーセプトロンニューラルネットワークをトレーニングする方法
4. 単純なニューラルネットワークトレーニングを理解する
5. ニューラルネットワークのトレーニング理論の概要
6. ニューラルネットワークの学習率を理解する
7. 多層パーセプトロンを使用した高度な機械学習
8. シグモイド活性化関数：多層パーセプトロンニューラルネットワークでの活性化
9. 多層パーセプトロンニューラルネットワークをトレーニングする方法
10. 多層パーセプトロンのトレーニング式とバックプロパゲーションを理解する
11. Python実装のためのニューラルネットワークアーキテクチャ
12. Pythonで多層パーセプトロンニューラルネットワークを作成する方法
13. ニューラルネットワークを使用した信号処理：ニューラルネットワーク設計での検証
14. ニューラルネットワークのデータセットのトレーニング：Pythonニューラルネットワークをトレーニングおよび検証する方法
15. ニューラルネットワークにはいくつの隠しレイヤーと隠しノードが必要ですか？
16. 隠れ層ニューラルネットワークの精度を高める方法

隠れ層に含まれるノードの数は、パーセプトロンニューラルネットワークの分類能力と速度に影響を与えます。適度な時間内にトレーニングし、許容可能なレイテンシで出力値を生成し、精度要件を満たすネットワークを設計する試みに、隠れ層の次元がどのように適合するかについて、いくつかの初期の直感を定式化するのに役立つ実験を実行します。 。

Pythonでのベンチマーク

パート12で紹介されているニューラルネットワークのPythonコードには、トレーニング済みのネットワークを使用して検証データセットからサンプルを分類することで精度を計算するセクションがすでに含まれています。したがって、必要なのは、トレーニング（フィードフォワード操作とバックプロパゲーションを含む）および実際の分類機能（フィードフォワード操作のみを含む）の実行時間を報告するコードを追加することだけです。 time.perf_counter（）を使用します このための機能。

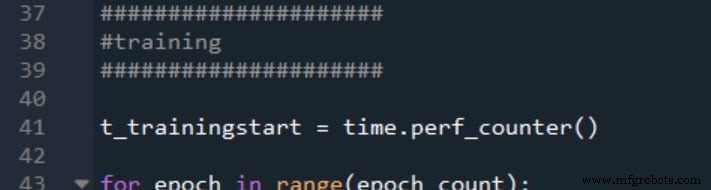
これが私がトレーニングの開始と終了をマークする方法です：

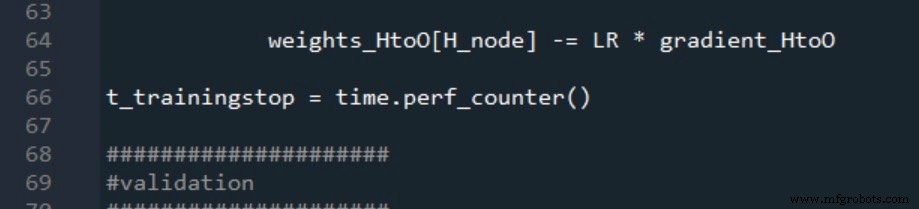
検証の開始時間と停止時間は同じ方法で生成されます：

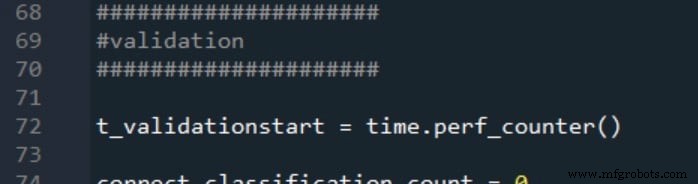
2つの処理時間の測定値は、次のように報告されます。

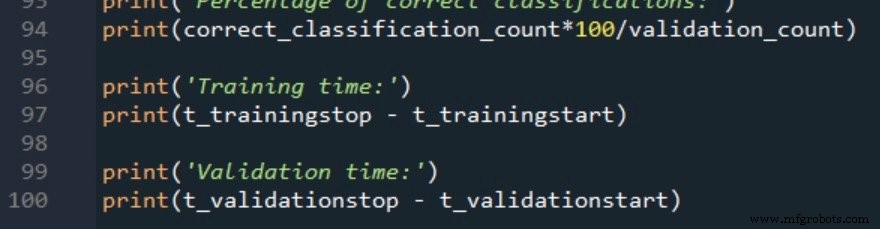
トレーニングデータと測定手順

ニューラルネットワークは、–20〜 +20の4つの数値で構成される入力サンプルに対して真/偽の分類を実行します。

したがって、4つの入力ノードと1つの出力ノードがあり、入力値は次のExcelの式で生成されます。

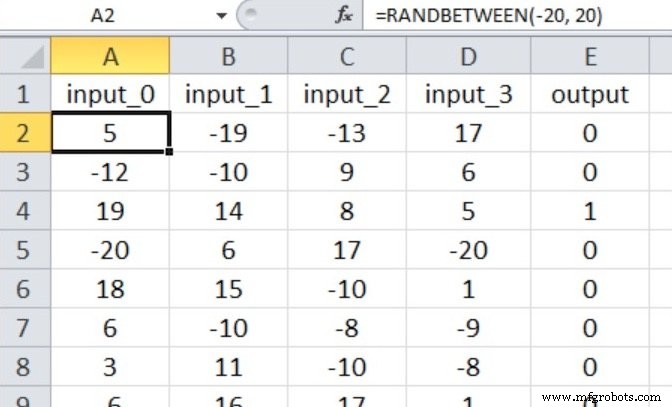
私のトレーニングデータセットは40,000サンプルで構成され、検証セットには5000サンプルが含まれています。学習率は0.1で、トレーニングエポックを1つだけ実行しています。

複雑さの程度が異なる入出力関係を表す3つの実験を実行します。 np.random.seed（1） ステートメントはコメント化されているため、初期の重み値は変化し、したがって分類の精度も変化します。

各実験では、プログラムは各隠れ層の次元に対して5回（同じトレーニングおよび検証データを使用して）実行され、精度と処理時間の最終測定値は、5回の別々の実行によって生成された結果の算術平均になります。 。

実験1：複雑度の低い問題

この実験では、以下のExcelスクリーンショットに示すように、最初の3つの入力がゼロより大きい場合にのみ出力が真になります（4番目の入力は出力値に影響を与えないことに注意してください）。

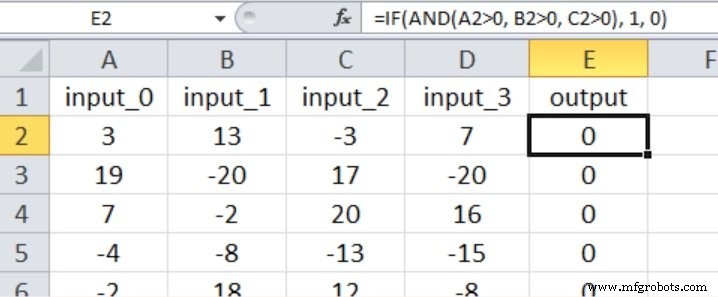
これは、多層パーセプトロンのかなり単純な入出力関係と見なされると思います。

ニューラルネットワークに必要なレイヤーとノードの数に関してパート15で提供した推奨事項に基づいて、入力次元の3分の2に等しい隠れ層の次元から始めます。

ノードの一部で非表示のレイヤーを作成することはできないため、 H_dim =2 から始めます。 。次の表に結果を示します。

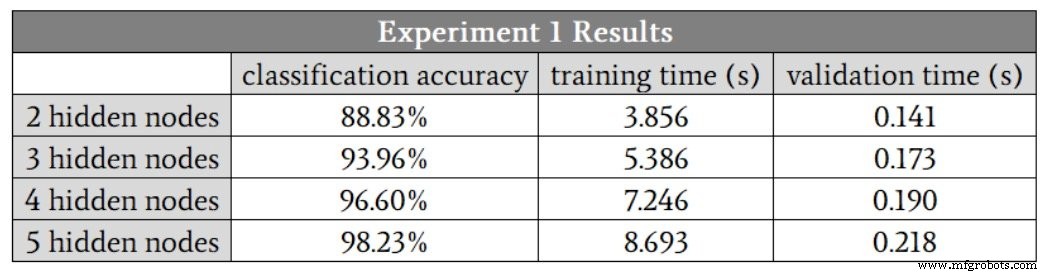
5つの隠れノードに至るまで分類の改善が見られます。ただし、4つの隠れノード実行の1つの精度が88.6％であり、これが平均を引き下げたため、これらの数値は4ノードから5ノードに増やすことの利点を誇張していると思います。

その低精度の実行を排除すると、4つの非表示ノードの平均精度は、実際には5つの非表示ノードの平均よりもわずかに高くなります。この場合、4つの隠れノードが精度と速度の最適なバランスを提供すると思います。

これらの結果で注目すべきもう1つの重要な点は、隠れ層の次元がトレーニング時間と処理時間にどのように影響するかという違いです。 2つから4つの非表示ノードに移動すると、検証時間が1.3倍になりますが、トレーニング時間が1.9倍になります。

トレーニングはフィードフォワード処理よりもはるかに計算量が多いため、ネットワーク構成が妥当な時間内にネットワークをトレーニングする能力にどのように影響するかについて特に注意する必要があります。

実験2：中程度の複雑さの問題

Excelのスクリーンショットは、この実験の入出力関係を示しています。 4つの入力すべてが出力値に影響を与えるようになり、比較は実験1の場合よりも簡単ではなくなりました。

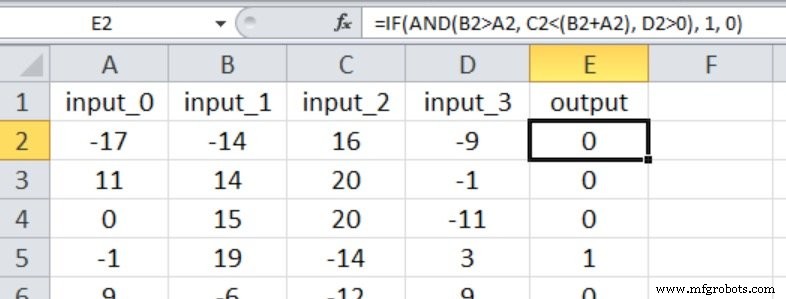
私は3つの隠しノードから始めました。結果は次のとおりです。

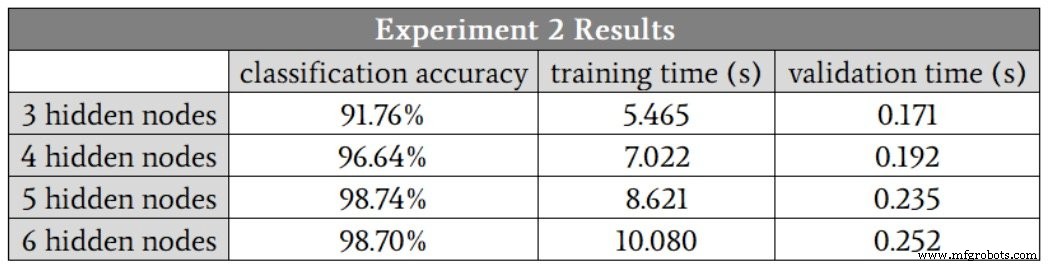
この場合、5つの隠れノードが精度と速度の最良の組み合わせを提供すると思いますが、4つの隠れノードの実行では、他のノードよりも大幅に低い1つの精度値が生成されました。この外れ値を無視すると、4つの非表示ノード、5つの非表示ノード、および6つの非表示ノードの結果は非常によく似ています。

5つの隠れノードと6つの隠れノードの実行で外れ値が生成されなかったという事実は、興味深い可能性のある発見につながります。おそらく、隠れ層の次元を増やすと、何らかの理由でトレーニングが発生する条件に対してネットワークがより堅牢になります。特に難しい。

実験3：複雑性の高い問題

以下に示すように、新しい入出力関係には4つの入力値すべてが含まれ、入力の1つを二乗し、別の入力の平方根を取ることによって非線形性を導入しました。

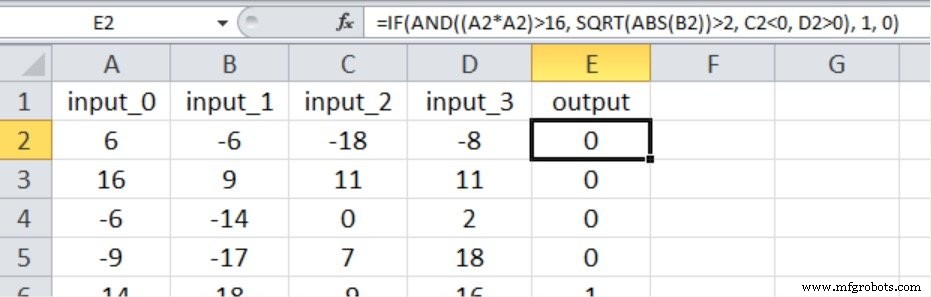
結果は次のとおりです。

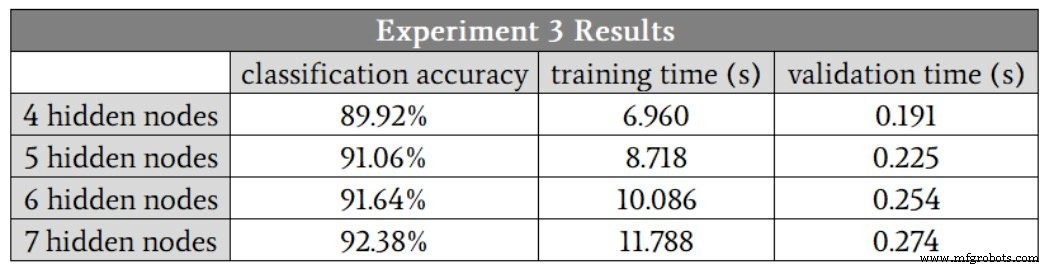
ネットワークは、このより複雑な数学的関係で間違いなくより困難でした。隠れノードが7つある場合でも、複雑度の低い問題で隠れノードが3つしかない場合よりも精度が低くなりました。バイアス（パート11を参照）や学習率のアニーリング（パート6を参照）など、ネットワークの他の側面を変更することで、複雑度の高いパフォーマンスを改善できると確信しています。

それでも、他の拡張機能によってネットワークがより小さな隠れ層で適切なパフォーマンスを維持できると完全に確信するまで、隠れ層の次元を7に保ちます。

結論

隠れ層の次元とパーセプトロンのパフォーマンスとの関係をかなり明確に描く興味深い測定値をいくつか見てきました。確かに、調査できる詳細は他にもたくさんありますが、これにより、ニューラルネットワークの設計とトレーニングを実験するときに利用できる確かな基礎情報が得られると思います。