二重界面スピン伝達トルク磁気トンネル接合におけるDzyaloshinskii-Moriya相互作用によって変調された磁化ダイナミクス

はじめに

磁気ランダムアクセスメモリ（MRAM）は、低消費電力、高密度、高速アクセス速度、ほぼ無限の耐久性、およびCMOSテクノロジとの優れた互換性により、次世代の不揮発性メモリの最も有望な候補の1つです[1 2]。 MRAMの基本的なデバイスは、磁気トンネル接合（MTJ）です。これは、2つの強磁性層（ピン層と自由層と呼ばれる）の間に挟まれたトンネルバリアで構成されています。垂直異方性の進歩の恩恵を受けて、MTJのフィーチャサイズは40nmまたは1×nm未満にスケーリングされました[3,4,5]。ただし、サブ40 nm MTJの課題は、適切な熱安定性バリア E を維持することです。 =μ ₀ M _s H _k V / 2。 （μを使用 ₀ 真空透磁率、 M _s 飽和磁化、 H _k 異方性フィールド、 V 自由層の体積）。この式で示されるように、 E MTJのスケーリングに伴って減少し、その結果、データ保持時間が短縮されます。この課題を克服するために、十分に高い E を達成するためにダブルインターフェースMTJが提案されました。 サブ40nmテクノロジーノード[6,7,8,9,10]。複合自由層として2つの結合された強磁性層を使用することにより、等価体積（ V ）二重界面では、熱安定性バリアを強化するためにMTJが増加します。その間、低いスイッチング電流を維持するためにダンピング定数が減少します。

ダブルインターフェースMTJでは、強磁性体/重金属（FM / HM）構造が性能の最適化に重要な役割を果たします。一方では、FM / HM構造により、スピン軌道相互作用（SOC）が増加し、垂直異方性が誘導されます。一方、重金属は、複合自由層の2つの強磁性層の間のスペーサーとして機能し、Ruderman-Kittel-Kasuya-Yosida（RKKY）相互作用[11]を提供します。これにより、2つの強磁性層の磁化がそれらが同一のレイヤーのように動作するように順序付けます。さらに、最近の研究は、強磁性体の原子スピンと結合する重金属の強いSOCが、Dzyaloshinskii-Moriya相互作用（DMI）と呼ばれる非対称交換結合を形成する可能性があることを示しています[12、13]。したがって、DMIはFM / HM構造を持つダブルインターフェースMTJで自然に誘導されます。最近の研究[14,15,16,17,18,19,20,21]で検証されているように、DMIはキラル磁気テクスチャ（スピンスパイラル、スキルミオン、ニール型磁壁など）を優先し、磁化ダイナミクスに劇的な影響を与えます。 、22、23、24、25]。 2つのFM / HMインターフェースを追加のRKKY相互作用とともに考慮する必要があるため、ダブルインターフェースMTJではDMIの役割がより複雑になることに注意することが重要です。したがって、ダブルインターフェイスMTJに対するDMIの影響を明らかにすることは重要です。

この手紙では、初めて、DMIとRKKY相互作用の作用下でのダブルインターフェースMTJのスイッチングプロセスを研究します。ダブルインターフェースMTJは、MRAMのデータ書き込みの主流のアプローチであるスピン転送トルク（STT）によって切り替えられます。最近、DMIがSTTスイッチングに悪影響を与えることが報告されました[21、22]。ここで、我々の結果は、ダブルインターフェースMTJでは、DMIの有害な影響がRKKY相互作用によって抑制され、高速スイッチングとより均一なダイナミクスをもたらす可能性があることを示しています。私たちの仕事は、負の界面効果に対するダブルインターフェースSTT-MTJの堅牢性を証明しています。

メソッド

この研究で研究された装置は、複合自由層としてFM / HM / FM構造を備えた図1aに示されています。 HM層の厚さは、誘導されたRKKY相互作用が2つのFM層を強磁性的に結合するように、適切な値に調整されます。 FM層の1つは磁気的に柔らかく、FL1（自由層1）として示され、もう1つは磁気的に硬く、FL2（自由層2）として示されます。複合自由層の磁化を切り替えるために、電流が二重界面MTJに印加され、STTを生成します。この作業では、参照層からFL1に送信されたSTTのみを考慮し、FL1とFL2の間の他のトルクは無視します。この簡略化されたモデルは、以前に報告された研究[26,27,28]と一致しています。 DMIはFM / HMとHM / FMの両方のインターフェースで誘導され、キラリティーが異なるために反対の符号を持ちます[29]。

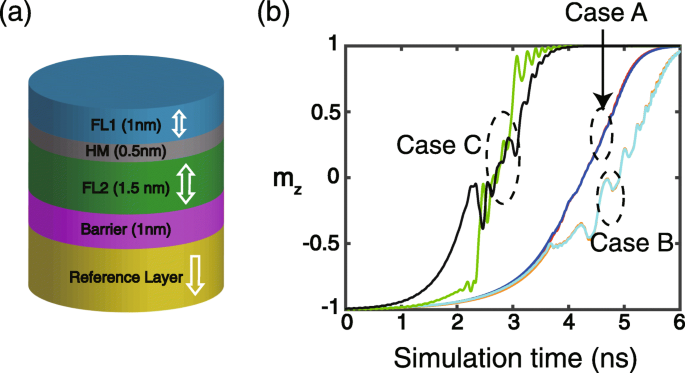
a この研究で研究されたデバイスの概略構造。わかりやすくするために、他のレイヤーは表示されていません。 b 時間依存の m の典型的な結果 _z （単位磁化の垂直成分）。ケースA：σ=1×10 ⁻³ J / m ² 、 D ₁ = D ₂ =0（FL1の場合は赤、FL2の場合は青）。ケースB：σ=1×10 ⁻³ J / m ² 、 D ₁ =1 mJ / m ² 、 D ₂ =-1 mJ / m ² （FL1の場合はオレンジ、FL2の場合はシアン）。ケースC：σ=1×10 ⁻⁴ J / m ² 、 D ₁ = D ₂ =0（FL1の場合は緑、FL2の場合は黒）

二重界面MTJにおけるFL1とFL2の磁化ダイナミクスをマイクロマグネティックシミュレーションによって研究します。単位磁化ベクトルの時間発展は、次のランダウ-リフシッツ-ギルバート（LLG）方程式によって支配されます。オープンソースのマイクロマグネティックシミュレーションツールであるOOMMFパッケージ[30]を選択して、デバイス構造をモデル化し、磁化ダイナミクスを分析するためのLLG方程式を解きます。

ここで、γ は磁気回転比、 m は磁化に沿った単位ベクトル z は厚さ方向に沿った単位ベクトル H _eff は、一軸垂直異方性、6近傍交換エネルギー、DMIフィールド、RKKY相互作用、減磁フィールド、双極子相互作用、およびSTTを含む有効場です。特に明記されていない限り、その他のパラメーターとそのデフォルト値を表1に示します。これらのパラメータ値は、最先端のテクノロジーに準拠しています。 DMIの大きさについては、ダブルインターフェイスMTJのCoFeB / W / CoFeB複合自由層を検討します[10、31、32、33]。報告されているW / CoFeBの実験的DMI結果は、0.12 mJ / m ² とは異なります。 〜0.73 mJ / m ² [34,35,36]。シミュレーションでは、DMIの大きさの範囲を±2mJ / m ² に拡張します。 一般的な研究のために。

一対の磁気モーメント間のRKKYエネルギー m _i および m _j E として定義されます _ij =σ [1 − m _i ∙ m _j ] / ∆ _ij 、ここで m _i および m _j それぞれFL1とFL2の磁気モーメントです。 σ は、2つのサーフェス間の双線形サーフェス交換係数です。 ∆ _ij は、セル i からの方向の任意のセルサイズです。 セル j に向かって 。この作業では、FL1とFL2が強磁性的に結合され、次にσ> 0は、RKKY相互作用が m になる傾向があることを意味します _i m に平行 _j 。 DMIは隣接するアトミックスピン S に作用します ₁ および S ₂ 大きなSOCを持つ3番目の原子を介して。対応するDMIハミルトニアンは H として表されます _DM =− D ₁₂ ∙（ S ₁ × S ₂ ）、ここで D ₁₂ DMIベクトルです[37]。したがって、DMIは S 間の均一性を低下させます ₁ および S ₂ 、RKKY相互作用と競合します。

結果と考察

まず、時間依存の m の典型的なシミュレーション結果 _z （単位磁化の垂直成分）を図1bに示します。 RKKY相互作用が十分に強い場合（例：σ=1×10 ^-3 J / m ² ケースAとケースB）の場合、FL1とFL2は結合されているため、DMIが考慮されているかどうかに関係なく、それらの磁化ダイナミクスはほぼ同じです。また、DMIの導入により、磁化スイッチングのプロセスが歪むことがわかります（ケースBを参照）。これは、報告された結果[21、22、23]と一致しており、DMIの非対称交換に起因する可能性があります。 RKKY相互作用が十分に強くないと、FL1とFL2の磁化ダイナミクスを理想的に結合できなくなるため、それらの間に有意差が観察されます（ケースCを参照）。以下では、特に明記しない限り、シミュレーション結果は十分に強いRKKY相互作用の下で得られます。

その後、さまざまなRKKY相互作用の下でのスイッチング速度を調べます。スイッチング速度は、 m の時間に反映されます。 _z 0（スイッチング時間として定義）に達します。 D ₁ および D ₂ それぞれ正の値と負の値に設定されます[29]。対応する結果を図2に示します。DMIがない場合、他の報告された結果と一致して、RKKY相互作用の強化に伴ってスイッチング時間が増加します[26、27、28、38]。その理由は、RKKY相互作用が強いと、FL1とFL2の磁化ダイナミクスがよりコヒーレントになり、複合自由層の異方性が同等に増加するためです。ただし、DMIが存在する場合、スイッチング時間のRKKY強度への依存性はより混沌とします。このカオスは、主にFL1とFL2の間の異方性の不一致に起因します。詳細については、後で説明します。これらの結果は、ダブルインターフェイスMTJのスイッチング動作に対するDMIの無視できない影響を示しています。

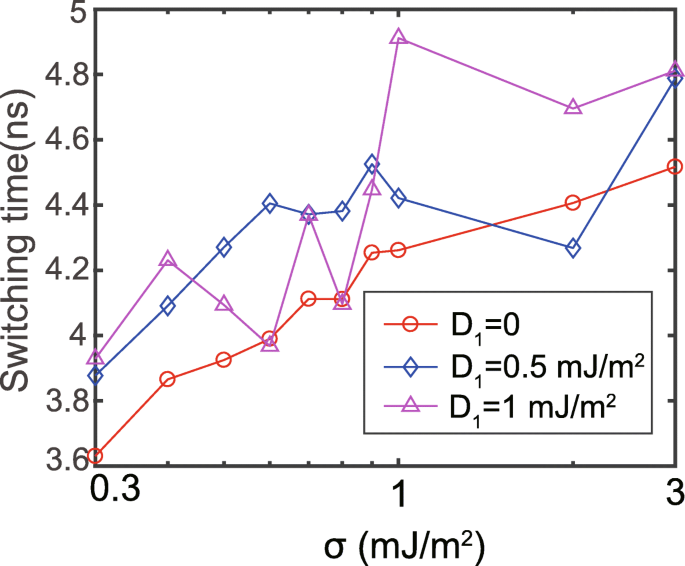
RKKY強度の関数としてのスイッチング時間。σは対数目盛で示されます。 D ₁ および D ₂ 同じ値に設定されていますが、符号が逆になっています

次に、DMIの効果をさらに詳しく調べます。図3は、DMI強度の関数としてのスイッチング時間を示しています。 D ₁ および D ₂ 実際には反対の符号を持っていますが、図3aでは意図的に同じ正の値に設定されています。言い換えれば、図3aは、シミュレーションモデルを検証するために調査する仮想ケースに対応します。物理理論の観点から、2つの正のDMIの有害な影響は、強磁性結合したRKKY相互作用の作用の下で累積されます。したがって、 D の増加に伴い、スイッチング時間は長くなると予想されます。 ₁ および D ₂ 、以前の作品で報告されているように[21、22]。この分析は、図3aに示す結果とよく一致しています。したがって、シミュレーションモデルの合理性が検証されます。図3aとは対照的に、 D を使用すると、DMIの悪影響を軽減できます。 ₁ および D ₂ 図3bに示すように、反対の符号があり、スイッチング時間の変動は図3aと比較してはるかに小さくなっています。図3bでは、曲線は正確に単調ではないことに注意してください。局所的な変動については後で説明します。注目すべきことに、2つのインターフェースでのDMIの影響は、 D の大きさを適切に調整することで相殺できます。 ₁ および D ₂ 、図3cに示すように。これらの結果は、キラリティー理論の観点から次のように説明できます。

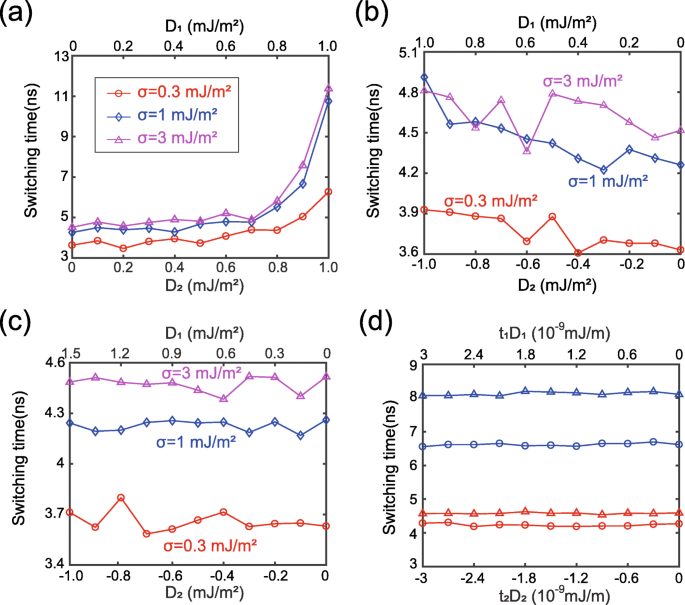
DMI強度の関数としてのスイッチング時間。 a D ₁ および D ₂ 同じ正の値に設定されます。 b D ₁ および D ₂ 同じ値に設定されますが、符号が逆になります。 c D ₁ および D ₂ t を満たすように構成されている ₁ D ₁ + t ₂ D ₂ =0。 d t を維持しながら、厚さまたは異方性定数を変更しながら追加の結果 ₁ D ₁ + t ₂ D ₂ =0.青い線： t ₁ 2nmに変更されます。赤い線： t ₁ 1.5nmに変更されます。三角形のデータ：σ=3×10 ⁻³ J / m ² 。サークルデータ：σ=1×10 ⁻³ J / m ²

DMIエネルギーは E として表されます _DM = t ∬ D [ m _x （∂m _z / ∂x ）− m _z （∂m _x / ∂x ）+ m _y （∂m _z / ∂y ）− m _z （∂m _y / ∂y ）] d ² r =tDε _DM [39]、ここで D は連続DMI定数、 t は強磁性層の厚さです。上記のように、FL1とFL2の磁化ダイナミクスは、十分に強いRKKY相互作用の下でほぼ同じです。この場合、同じε _DM FL1とFL2で取得されます。次に、FL1とFL2の合計DMIエネルギーは、 E によって計算できます。 _tot =（ t ₁ D ₁ + t ₂ D ₂ ）ε _DM 。したがって、 D を設定することにより ₁ / D ₂ =− t ₂ / t ₁ 、図3cと一致して、十分に大きいσの場合、FL1とFL2のDMI効果は完全に相殺される可能性があります。この結論は、図3dに示す追加の結果によってさらに検証されます。ここでは、 D を維持しながら、他のパラメーターを意図的に変更しています。 ₁ / D ₂ =− t ₂ / t ₁ 。

同等のDMIの大きさ（ D _eq ）複合自由層のは D として表すことができます _eq =（ t ₁ D ₁ + t ₂ D ₂ ）/（ t ₁ + t ₂ ）、これは、ダブルインターフェイスMTJに対するDMIの影響を定量的に分析するために使用できます。この方程式の有効性を検証するために、2つのグループのシミュレーション結果を図4aに示します。ここでは、2つの曲線が同じ D の下で取得されています。 _eq ただし、2組の異なる{ D ₁ 、 D ₂ それぞれ}値。 2つの曲線には少し違いがありますが、全体的な傾向は類似しており、STTスイッチングに対するDMIの悪影響を検証しています。ここで、2つの曲線の違いは次のように説明できます。 FL1とFL2は異方性定数が異なり、図4cに示すように、磁化ダイナミクスの局所的な不確実な振動を引き起こします。同じ現象が図2と図3bでも観察されます。代わりに、理想的なケースを図4b、dに示します。ここでは、FL1とFL2の異方性定数が同じ値に設定されています。明らかに、2つの曲線の間に良好な一致が見られ、上記の D の式が示されています。 _eq ダブルインターフェースMTJの同等のDMI効果を十分に説明できます。

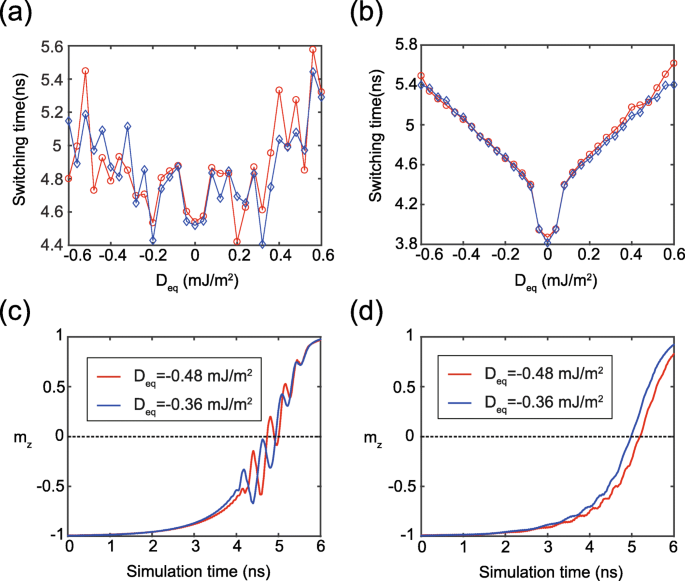
a 、 b D の関数としての切り替え時間 _eq 。各 D _eq 異なる{ D の2つのペアで取得されます ₁ 、 D ₂ D に従った}値 _eq =（ t ₁ D ₁ + t ₂ D ₂ ）/（ t ₁ + t ₂ ）。赤い曲線： D ₁ その間に変化する D ₂ 1 mJ / m ² に固定されています 。青い曲線： D ₁ および D ₂ 常に同じ値に設定されます。ここで、σ=1×10 ⁻² J / m ² 。 a で 、その他のパラメータは表1のように構成されています。 b 、 K _{u 1} = K _{u 2} =0.7mJ / m ³ 理想的な場合。 c 、 d 時間依存の m の典型的な結果 _z a に対応 および b 、それぞれ

最後に、磁化ダイナミクスの時間発展をより詳細に分析します。図5は、磁化スイッチング中の時間依存エネルギーを示しています。 FL1とFL2のDMIエネルギーは、 D の符号と大きさに応じて、累積またはキャンセルされます。 ₁ および D ₂ 。この傾向は、上記の理論モデルとよく一致しています。さらに、RKKYエネルギーは低い値に保たれ、FL1とFL2の磁気モーメントが同期して駆動されることを検証します。 RKKYフィールドとDMIフィールドの分布を図6に示します。ここで、RKKYフィールドはさまざまなケースで異なる役割を果たします。まず、非ゼロDMIの場合（ケース2およびケース3を参照）、RKKYフィールドはゼロDMIの場合（ケース1を参照）と比較してはるかに強力です。 ＲＫＫＹ場は、ＤＭＩの存在下での磁気テクスチャの追加の不均一性を克服しなければならないことが理解できた。次に、 D の場合 ₁ および D ₂ は反対の符号であり、RKKYフィールドはFL1とFL2の両方のDMIフィールドに抵抗します（ケース2を参照）。その結果、DMIが弱くなり、磁化ダイナミクスがより均一になります。対照的に、一度 D ₁ および D ₂ 同じ符号を持つRKKYフィールドは、一方の強磁性層ではDMIフィールドに抵抗しますが、もう一方の強磁性層ではそれを支援します（ケース3を参照）。したがって、全体的なDMIフィールドは、磁化ダイナミクスに一定の影響を及ぼします。これは、 D の場合、DMIをキャンセルできないことを検証します。 ₁ および D ₂ 同じ記号です。

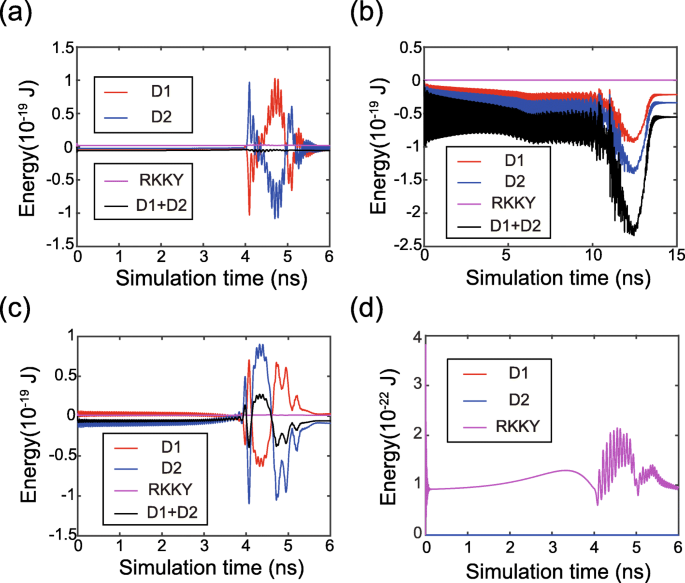
DMIおよびRKKYエネルギーの時間発展。 a D ₁ =1.5mJ / m ² 、 D ₂ =− 1 mJ / m ² つまり、DMI効果はキャンセルされます。 b D ₁ = D ₂ =1mJ / m ² つまり、DMI効果が蓄積されます。 c D ₁ =1mJ / m ² 、 D ₂ =− 1 mJ / m ² つまり、DMIの影響は軽減されますが、キャンセルされません。 d D ₁ = D ₂ =0

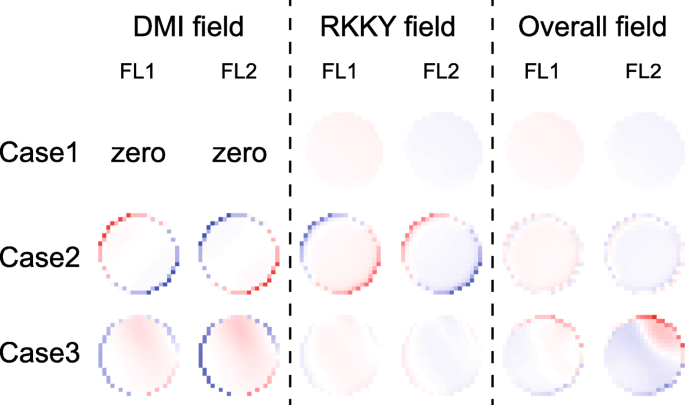
DMIおよびRKKYフィールドの空間分布。ここでは、それぞれの場合のある時点での典型的な結果が示されています。結論は他の時点では変更されていません。ケース1： D ₁ = D ₂ =0.ケース2： D ₁ =1.5mJ / m ² 、 D ₂ =− 1 mJ / m ² つまり、DMI効果はキャンセルされます。ケース3： D ₁ = D ₂ =1mJ / m ² 、つまり、DMI効果が蓄積されます

図7は、磁化スイッチング中のFL1とFL2のマイクロマグネティック構成を示しています。磁壁はすべての場合に現れますが、ある時点で異なる特徴が観察される可能性があります。 DMIが不均一な磁気テクスチャを優先することはよく知られています。それにもかかわらず、図7では、DMIが存在する場合でも均一な磁化が形成されます（ m _z =− 0.5（ケース2）の場合、DMI効果がキャンセルされている限り。この場合も、この結果は上記の理論モデルを検証します。さらに、 D の場合、磁化ダイナミクスがより不均一になることもわかります。 ₁ および D ₂ 上記の分析と一致して、同じ符号（磁壁が常に表示されるケース3を参照）です。また、より小さなMTJでシミュレートされたいくつかの結果を示します（図7の最後の2行を参照）。ケース2（DMIがキャンセルされていない）とケース3（DMIがキャンセルされていない）のマイクロマグネティック構成の違いはより顕著です。

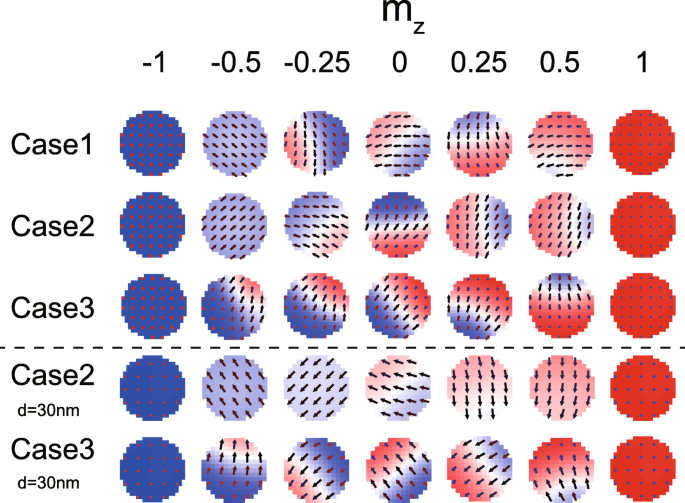
磁化スイッチング中のマイクロマグネティック構成。ここで、ケース1〜3は図6と同じパラメータで構成されています

結論

ダブルインターフェイスSTT-MTJに対するDMIの影響を包括的に調査しました。よく知られているように、二重界面MTJは、熱安定性バリアを強化するために開発されました。この作業では、私たちの結果は、ダブルインターフェイスMTJの別の利点、つまりDMIの悪影響を抑制することを証明しています。 2つの強磁性層のDMIは、適切な値と反対の符号で構成されている場合、抑制またはキャンセルされる可能性があります。これは、ダブルインターフェイスSTT-MTJ構造によって自然に満たされます。結論を説明するために理論モデルが提案された。磁化ダイナミクスにおいてDMIが果たした役割を明らかにするために、マイクロマグネティックシミュレーションの結果が議論されました。私たちの仕事は、ダブルインターフェースSTT-MTJのDMIを最小化するための実行可能なアプローチを提供します。

データと資料の可用性

すべてのデータは制限なしで完全に利用可能です。

略語

DMI：

DzyaloshinskiiとMoriyaの相互作用

FL：

フリーレイヤー

FM / HM：

強磁性体/重金属

MRAM：

磁気ランダムアクセスメモリ

MTJ：

磁気トンネル接合

RKKY：

Ruderman–Kittel–Kasuya–Yosida

SOC：

スピン軌道相互作用

STT：

スピン伝達トルク