合計と積の表記

参考までに、このセクションでは、カルノー図に割り当てられたmintermsとmaxtermsを説明するために一部のテキストで使用されている用語を紹介します。それ以外の場合、ここに新しい資料はありません。

Σ（シグマ）は合計を示し、小文字の「m」は最小項を示します。 Σmは最小項の合計を示します。次の例は、私たちのポイントを説明するために再検討されています。単純化されていないロジックのブール方程式の説明の代わりに、mintermsをリストします。

 f（A、B、C、D）=Σm（1、2、3、4、5、7、8、9、11、12、13、15） また f（A、B、C、D）=Σ（m ₁ 、m ₂ 、m ₃ 、m ₄ 、m ₅ 、m ₇ 、m ₈ 、m ₉ 、m ₁₁ 、m ₁₂ 、m ₁₃ 、m ₁₅ ）。

数字は、右下に示すように、カルノー図内のセルの位置またはアドレスを示します。これは確かに、Kマップ内の最小項またはセルのリストを記述するためのコンパクトな手段です。

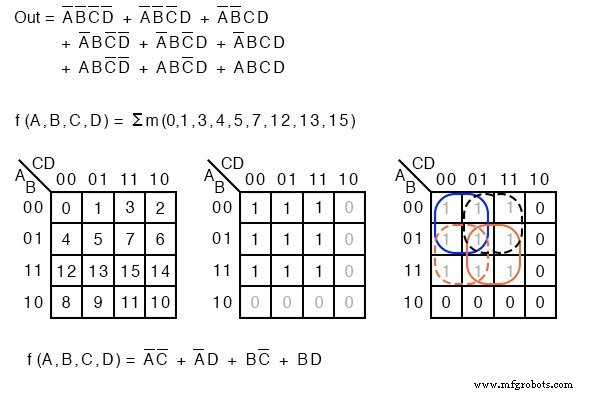
Sum-Of-Productsソリューションは、新しい用語の影響を受けません。ミンターム、 1 s、マップでは通常どおりグループ化され、Sum-OF-Productsソリューションが作成されています。

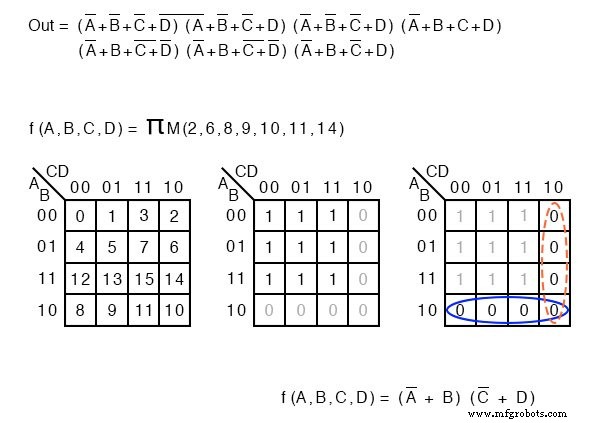
以下に、maxtermsのリストを説明するための用語を示します。製品はギリシャ語のΠ（pi）で示され、大文字の「M」はmaxtermsを示します。 ΠMはmaxtermsの積を示します。同じ例が私たちのポイントを示しています。

簡略化されていないロジックのブール方程式の説明は、maxtermsのリストに置き換えられます。

 f（A、B、C、D）=ΠM（2、6、8、9、10、11、14） また f（A、B、C、D）=Π（M ₂ 、M ₆ 、M ₈ 、M ₉ 、M ₁₀ 、M ₁₁ 、M ₁₄ ）。

繰り返しになりますが、数字はKマップセルのアドレス位置を示しています。 maxtermsの場合、これは 0 の場所です。 s、以下に示すように。 Product-OF-Sumsソリューションは通常の方法で完了します。

$$ Out =（A + B + \ bar {C} + D）（A + \ bar {B} + \ bar {C} + D）+（\ bar {A} + B + C + \ bar {D }）+（\ bar {A} + B + \ bar {C} + D）$$

$$（\ bar {A} + B + \ bar {C} + \ bar {D}）（\ bar {A} + \ bar {B} + \ bar {C} + D）$$

関連するワークシート：

産業技術