ミルマンの定理の再考
各分岐に直列抵抗と電圧源が含まれている回路の並列分岐全体の「ミルマン電圧」を決定するための奇妙な方程式がどこで得られたのか疑問に思われるかもしれません。

この方程式の一部は、これまでに見た方程式に馴染みがあるようです。たとえば、大部分の分母は、並列抵抗方程式の分母に非常によく似ています。そしてもちろん、大部分の分子のE / R項は、現在の数値を示す必要があります。オームの法則はそれが何であるか(I =E / R)です。
テブナンとノートンのソースの同等性について説明したので、ミルマンの方程式を理解するために必要なツールがあります。ミルマンの定理が実際に行っているのは、各分岐(直列の電圧源と抵抗を含む)をテブナンの等価回路として扱い、それぞれを等価のノートン回路に変換することです。
テブナン等価回路
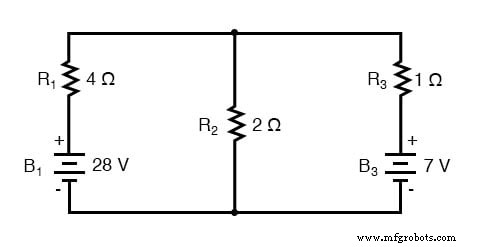
したがって、上記の回路では、バッテリーB1と抵抗R1は、4Ωの抵抗と並列に7アンペア(28ボルト/4Ω)のノートンソースに変換されるテブナンソースと見なされます。右端の分岐は、7アンペアの電流源(7ボルト/1Ω)と1Ωの抵抗に並列に変換されます。電圧源をまったく含まない中央の分岐は、2Ωの抵抗と並列に0アンペアのノートンソースに変換されます。
ノートンの定理
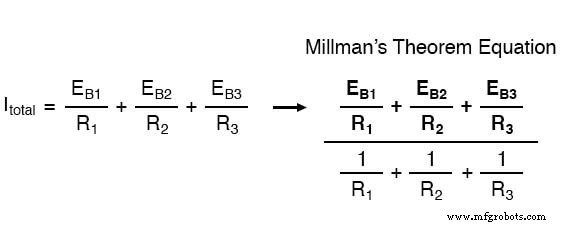
電流源はそれぞれの電流を直接並列に追加するため、合計回路電流は7 + 0 + 7、つまり14アンペアになります。ノートンソース電流のこの追加は、ミルマン方程式の分子で表されているものです:
ミルマン方程式

ノートンの抵抗はすべて、等価回路でも互いに並列であるため、減少して全体の抵抗が生成されます。このソース抵抗の減少は、ミルマンの方程式の分母に表されているものです。
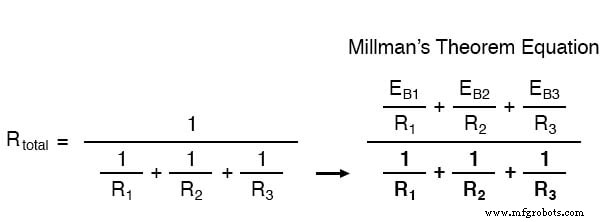
この場合、抵抗の合計は571.43ミリオーム(571.43mΩ)に等しくなります。これで、単一のノートン電流源とノートン抵抗を備えた等価回路を再描画できます。
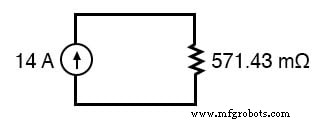
オームの法則により、これら2つのコンポーネント間の電圧がわかります(E =IR):
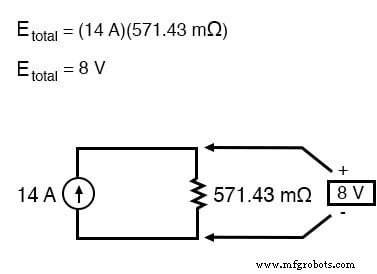
これまでの回路について私たちが知っていることを要約しましょう。この回路の総電流は、すべての分岐電圧の合計をそれぞれの抵抗で割ったものであることがわかっています。また、すべての分岐抵抗の逆数の逆数を取ることによって、総抵抗が求められることもわかっています。さらに、全電流に全抵抗(E =IR)を掛けることにより、すべての分岐の全電圧を求めることができるという事実を十分に認識しておく必要があります。私たちがする必要があるのは、総回路電流と総抵抗について以前に持っていた2つの方程式をまとめ、それらを乗算して総電圧を求めることです。
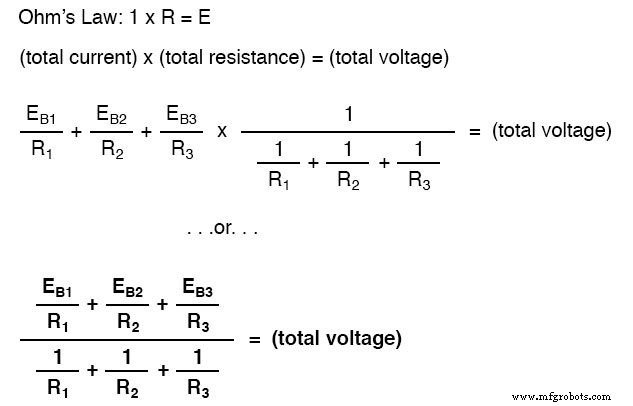
ミルマンの式は、テブナンからノートンへの変換を並列抵抗の式と組み合わせて、回路のすべての分岐にわたる合計電圧を求めることにすぎません。だから、うまくいけば、謎のいくつかは今なくなっています!
関連ワークシート:
- ミルマンの定理ワークシート
産業技術



