直列抵抗-インダクタ回路
前のセクションでは、単純な抵抗のみおよびインダクタのみのAC回路で何が起こるかを調べました。次に、2つのコンポーネントを直列に混合し、効果を調査します。
直列抵抗インダクタ回路の例
使用する例としてこの回路を取り上げます:
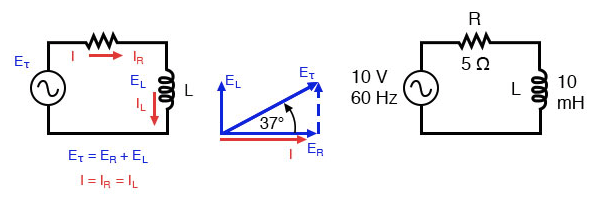
直列抵抗インダクタ回路:電流は印加電圧より0oから90o遅れます。
抵抗は周波数に関係なくAC電流に対して5Ωの抵抗を提供し、インダクタは60HzでAC電流に対して3.7699Ωのリアクタンスを提供します。
抵抗器の抵抗は実数(5Ω∠0°、または5 +j0Ω)であり、インダクタのリアクタンスは虚数(3.7699Ω∠90°、または0 +j3.7699Ω)であるため、 2つの成分は、2つの数値の複素数の合計に等しい電流に対抗します。
この組み合わされた反対は、抵抗とリアクタンスのベクトルの組み合わせになります。この反対を簡潔に表現するには、抵抗またはリアクタンスだけの場合よりも、電流に対する反対のより包括的な用語が必要です。
この用語はインピーダンスと呼ばれます 、その記号はZであり、抵抗やリアクタンスと同様に、オームの単位でも表されます。上記の例では、合計回路インピーダンスは次のとおりです。

オームの法則への抵抗
インピーダンスは、オームの法則の抵抗と同じように、予想どおりに電圧と電流に関連しています。

実際、インピーダンスが抵抗よりもはるかに包括的な電流の流れに対する反対の表現であるように、これはDCエレクトロニクス(E =IR)で教えられたものよりもはるかに包括的なオームの法則です。 任意 抵抗とリアクタンスは、個別にまたは組み合わせて(直列/並列)、AC回路で単一のインピーダンスとして表すことができます。
上記の回路の電流を計算するには、最初に電圧源の位相角基準を与える必要があります。これは一般にゼロと見なされます。 (抵抗性インピーダンスと誘導性インピーダンスの位相角は常に 電圧または電流の特定の位相角に関係なく、それぞれ0°および+ 90°)。
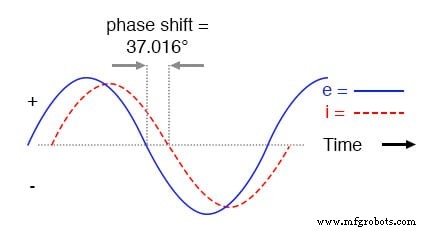
純粋な誘導回路と同様に、電流波は(ソースの)電圧波より遅れますが、今回の遅れはそれほど大きくありません。純粋な誘導回路の場合のように完全な90°ではなく、37.016°だけです。 。

直列L-R回路の電流は電圧より遅れます。
抵抗器とインダクターについては、電圧と電流の位相関係は変化していません。抵抗器の両端の電圧は、抵抗器を流れる電流と同相(0°シフト)であり、インダクターの両端の電圧は、抵抗器を流れる電流と+ 90°位相がずれています。これは数学的に検証できます:

抵抗器の両端の電圧は、抵抗器を流れる電流とまったく同じ位相角を持ち、EとIが同相であることを示しています(抵抗器の場合のみ)。

インダクタの両端の電圧の位相角は52.984°ですが、インダクタを流れる電流の位相角は-37.016°で、2つの間に正確に90°の差があります。これは、EとIがまだ90°位相がずれていることを示しています(インダクターの場合のみ)。
キルヒホッフの電圧法則を使用する
キルヒホッフの電圧法則が予測するように、これらの複素数値が加算されて合計電圧になることを数学的に証明することもできます。

SPICEを使用して計算する
SPICEを使用して計算の妥当性を確認しましょう:
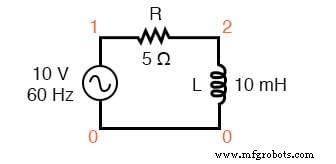
スパイス回路:R-L。
v1 1 0 ac 10 sin r1 1 2 5 l1 2 0 10m .ac lin 1 60 60 .print ac v(1,2)v(2,0)i(v1) .print ac vp(1,2)vp(2,0)ip(v1) 。終わり
freq v(1,2)v(2)i(v1) 6.000E + 01 7.985E + 00 6.020E + 00 1.597E + 00 freq vp(1,2)vp(2)ip(v1) 6.000E + 01 -3.702E + 01 5.298E + 01 1.430E + 0

DC回路の場合と同様に、SPICEは、供給電圧に対して負(180°位相がずれている)であるかのように電流値を出力することに注意してください。 -37.016°の位相角の代わりに、143°(-37°+ 180°)の現在の位相角が得られます。
これは単にSPICEの特異性であり、回路シミュレーション自体に重要なことを表すものではありません。抵抗器とインダクターの電圧位相の読み取り値が、予想どおりに計算値(それぞれ、-37.02°と52.98°)と一致していることに注意してください。
このような単純な回路でも追跡するこれらすべての数値を使用すると、「テーブル」方式を使用することが有益になります。この単純な直列抵抗-インダクタ回路にテーブルを適用すると、そのまま続行されます。
まず、E / I / Zの数値の表を作成し、これらの用語のすべてのコンポーネント値を挿入します(つまり、実際の抵抗値またはインダクタンス値をそれぞれオームとヘンリーで表に挿入するのではなく、変換します。インピーダンスの複雑な数値に変換し、それらを書き込みます):
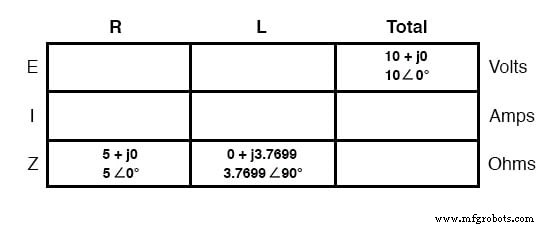
必須ではありませんが、両方と書くと便利です。 表の各量の長方形と極形式。長方形と極形式の間の変換を必要とせずに複雑な算術を実行する機能を備えた計算機を使用している場合、この追加のドキュメントは完全に不要です。
ただし、複雑な算術「ロングハンド」(長方形形式での加算と減算、極形式での乗算と除算)を実行する必要がある場合は、両方の形式で各量を書き込むと便利です。
「与えられた」数値が表のそれぞれの位置に挿入されたので、DCの場合と同じように進めることができます。つまり、個々のインピーダンスから合計インピーダンスを決定します。これは直列回路であるため、電流の流れに逆らうことがわかります(抵抗または インピーダンス)を追加して、完全な反対を形成します:
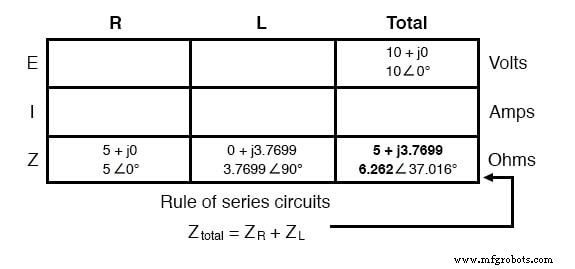
総電圧と総インピーダンスがわかったので、オームの法則(I =E / Z)を適用して総電流を決定できます。
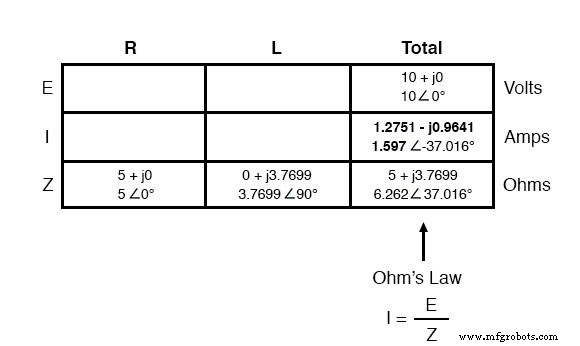
DCの場合と同様に、直列AC回路の合計電流はすべてのコンポーネントで均等に共有されます。直列回路には電流が流れる経路が1つしかないため、これは依然として当てはまります。したがって、それらの流れの速度は全体にわたって均一でなければなりません。したがって、電流の数値を抵抗とインダクタの列に同様に転送できます。
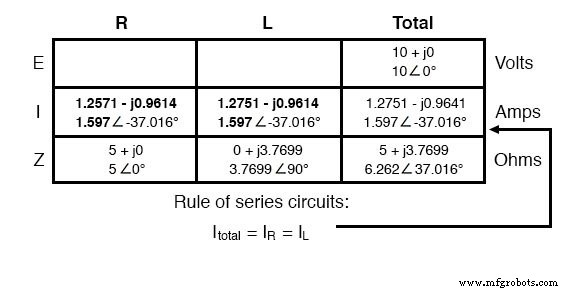
あとは、抵抗とインダクタのそれぞれの両端の電圧降下だけです。これは、表の各列に垂直に適用されるオームの法則(E =IZ)を使用して行われます:
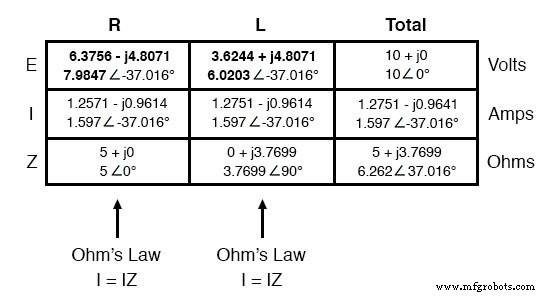
これで、テーブルが完成しました。 DC回路の分析で適用したのとまったく同じ規則がAC回路にも適用されますが、すべての量はスカラー形式ではなく複雑な形式で表現および計算する必要があることに注意してください。
位相シフトが計算で適切に表現されている限り、基本的なAC回路解析とDCのアプローチに基本的な違いはありません。
今こそ、これらの計算された数値と、実際の機器による電圧と電流の測定値との関係を確認する良い機会です。
ここで実際の測定値に直接関連する数値は、極座標表記の数値です。 、長方形ではありません!つまり、この回路の抵抗の両端に電圧計を接続すると、 7.9847 を示します。 6.3756(実際の長方形)または4.8071(想像上の長方形)ボルトではなく、ボルト。
これをグラフで説明すると、測定器は、その特定の量(電圧または電流)に対するベクトルの長さを単純に示します。
長方形の表記法は、算術的な加算と減算には便利ですが、実際の測定値に関しては、極座標よりも抽象的な形式の表記法です。前に述べたように、数学的な計算の便宜のために、AC回路テーブルに各量の極形と長方形の両方を示します。
これは絶対に必要というわけではありませんが、高度な計算機を利用せずにフォローしている人には役立つ場合があります。 1つの表記法のみの使用に制限する場合、実際の測定値に直接相関させることができるのは極性であるため、最良の選択は極性になります。
直列R-L回路のインピーダンス(Z)は、抵抗(R)と誘導性リアクタンス(XL)が与えられた場合に計算できます。 E =IR、E =IXL、およびE =IZであるため、抵抗、リアクタンス、およびインピーダンスは、それぞれ電圧に比例します。したがって、電圧フェーザ図は、同様のインピーダンス図に置き換えることができます。
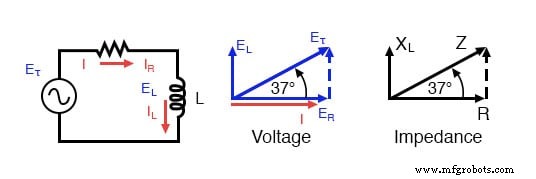
シリーズ:R-L回路のインピーダンスフェーザ図。
例: 与えられたもの:79.58ミリヘンリーインダクタと直列の40Ω抵抗。 60ヘルツでのインピーダンスを求めます。
XL =2πfL XL =2π・60・79.58×10-3 XL =30Ω Z =R + jXL Z =40 + j30 | Z | =sqrt(402 + 302)=50Ω ∠Z=アークタンジェント(30/40)=36.87° Z =40 + j30 =50∠36.87°
レビュー:
- インピーダンス は電流に対する反対の合計であり、(「実数」)抵抗と(「虚数」)リアクタンスの複素数(ベクトル)の合計です。抵抗(R)やリアクタンス(X)と同じように、文字「Z」で表され、オームで測定されます。
- インピーダンス(Z)は、直列回路解析の抵抗(R)と同じように管理されます。直列インピーダンスが加算されて、合計インピーダンスが形成されます。すべての計算は、必ず複雑な(スカラーではない)形式で実行してください。 Z 合計 =Z 1 + Z 2 +。 。 。 Z n
- 純粋な抵抗性インピーダンスの位相角は常に正確に0°です(ZR =RΩ∠0°)。
- 純粋な誘導インピーダンスは、常に正確に+ 90°の位相角を持ちます(ZL =XLΩ∠90°)。
- AC回路のオームの法則:E =IZ; I =E / Z; Z =E / I
- 回路内で抵抗とインダクタが混在している場合、合計インピーダンスの位相角は0°から+ 90°の間のどこかになります。回路電流の位相角は0°から-90°の間です。
- 直列AC回路は、直列DC回路と同じ基本特性を示します。電流は回路全体で均一であり、電圧降下が加算されて総電圧が形成され、インピーダンスが加算されて総インピーダンスが形成されます。
関連するワークシート:
- インダクタワークシート
- 抵抗、リアクタンス、およびインピーダンスのワークシート
- 誘導性リアクタンスワークシート
産業技術



