定在波と共振

伝送線路と負荷の間にインピーダンスの不一致があるときはいつでも、反射が起こります。入射信号が連続AC波形の場合、これらの反射は、より多くの対向入射波形と混合して、定在波と呼ばれる定常波形を生成します。 。

次の図は、三角形の入射波形が、ラインの終端されていない端に到達すると、どのように鏡像反射に変わるかを示しています。この例示的なシーケンスの伝送ラインは、簡単にするために、一対のワイヤではなく、単一の太いラインとして示されています。

入射波は左から右に移動し、反射波は右から左に移動します:(下の図）

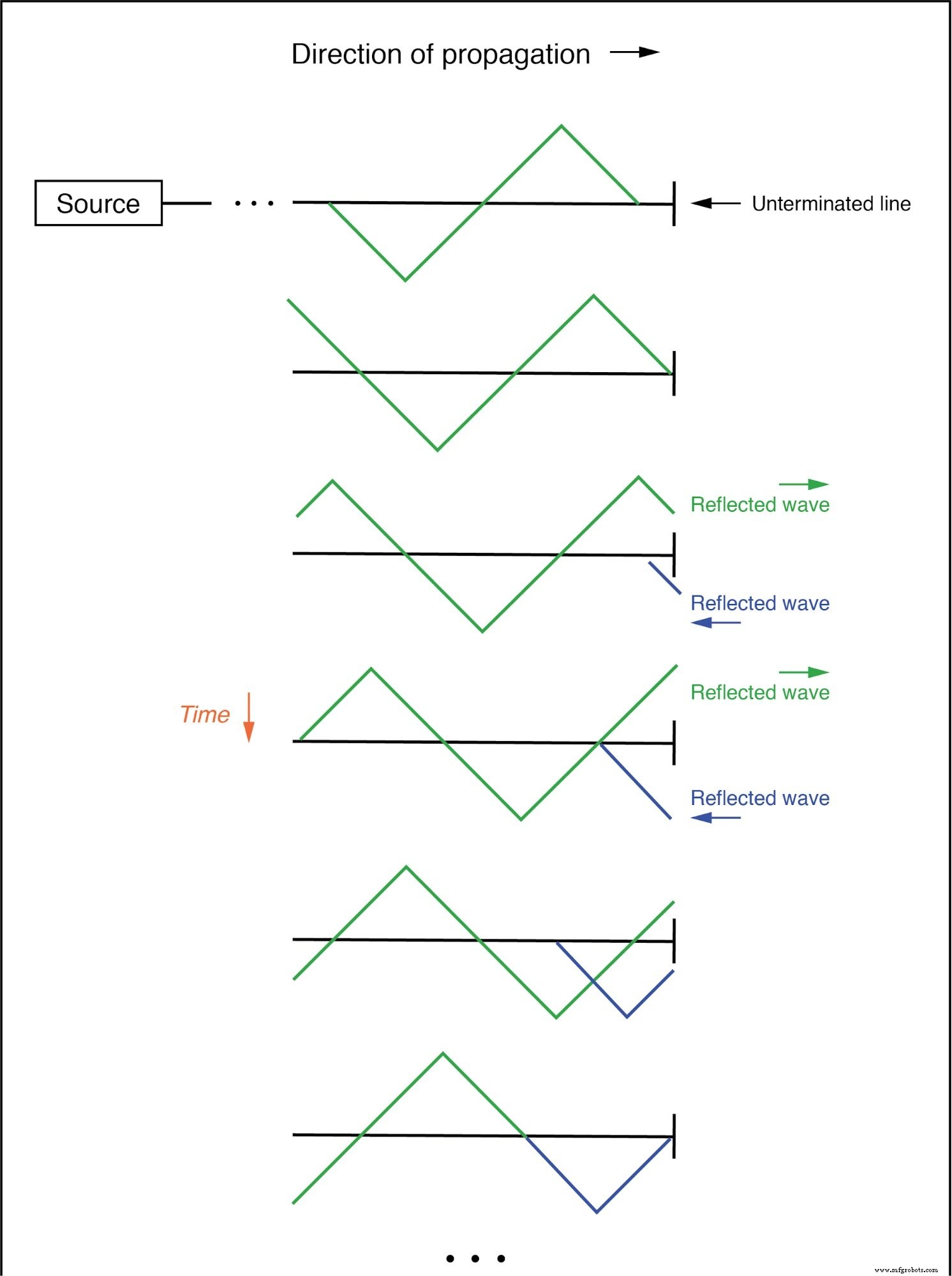
入射波は終端されていない伝送線路の端で反射します。

2つの波形を足し合わせると、線の長さに沿って3番目の定常波形が作成されることがわかります:(下の図）

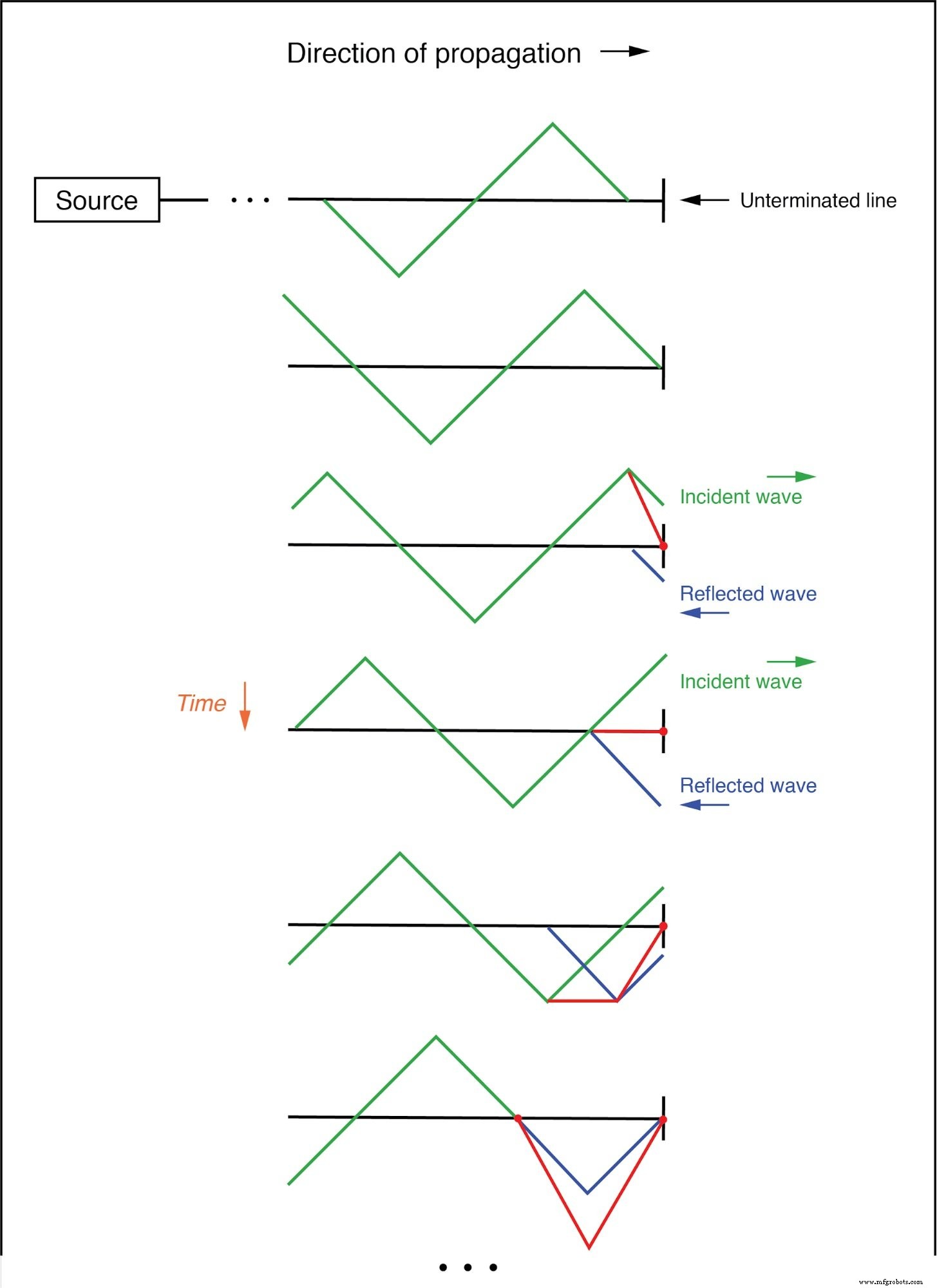
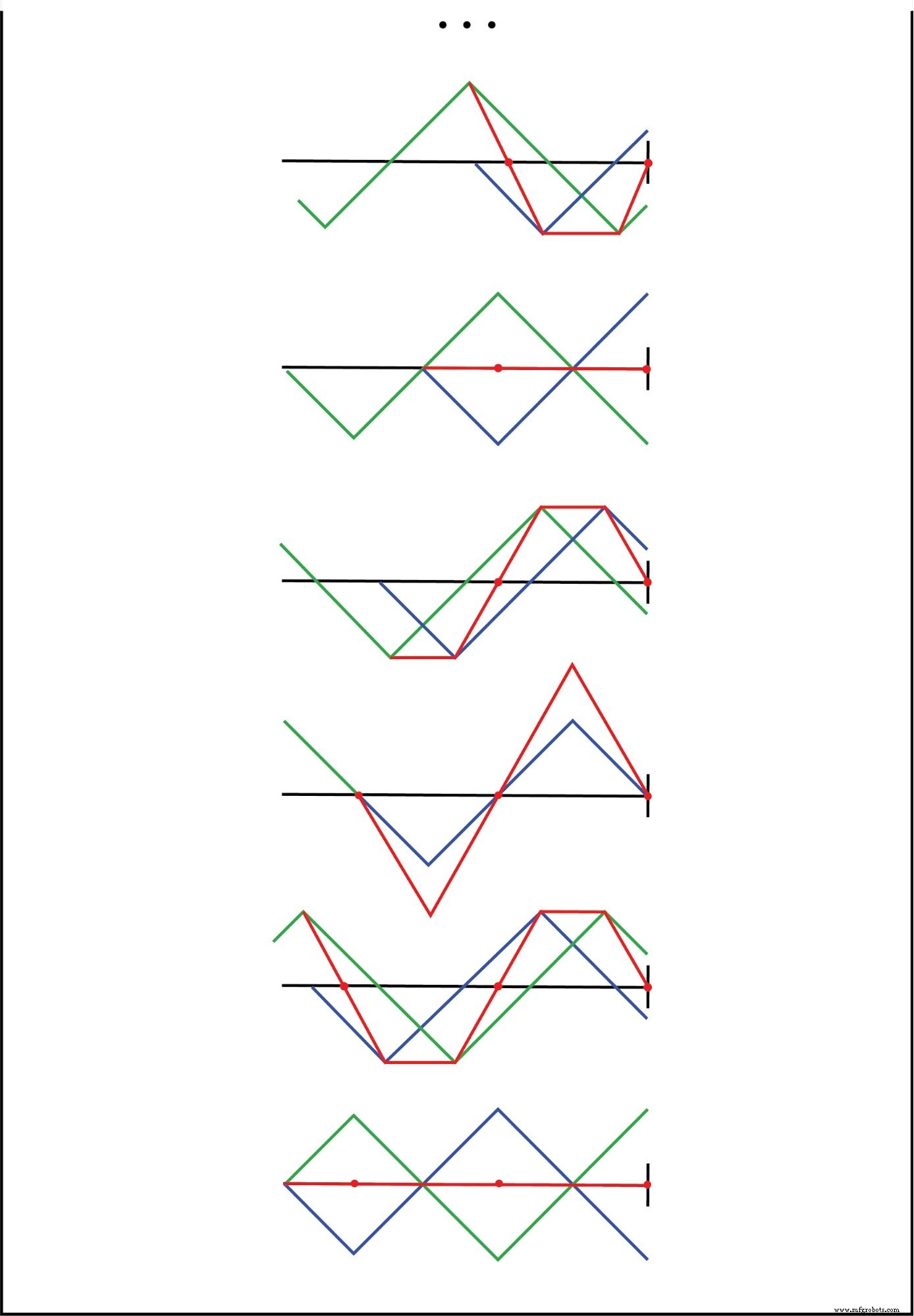
入射波と反射波の合計は定在波です。

実際、この3番目の「定在」波は、線に沿った唯一の電圧を表しており、入射電圧波と反射電圧波の代表的な合計です。それは瞬間的な大きさで振動しますが、それを引き起こす入射波形や反射波形のようにケーブルの長さ方向に伝播することはありません。

定在波の「ゼロ」ポイント（入射波と反射波が互いに打ち消し合う）を示す線の長さに沿った点と、それらのポイントが決して位置を変えないことに注意してください:(下の図）

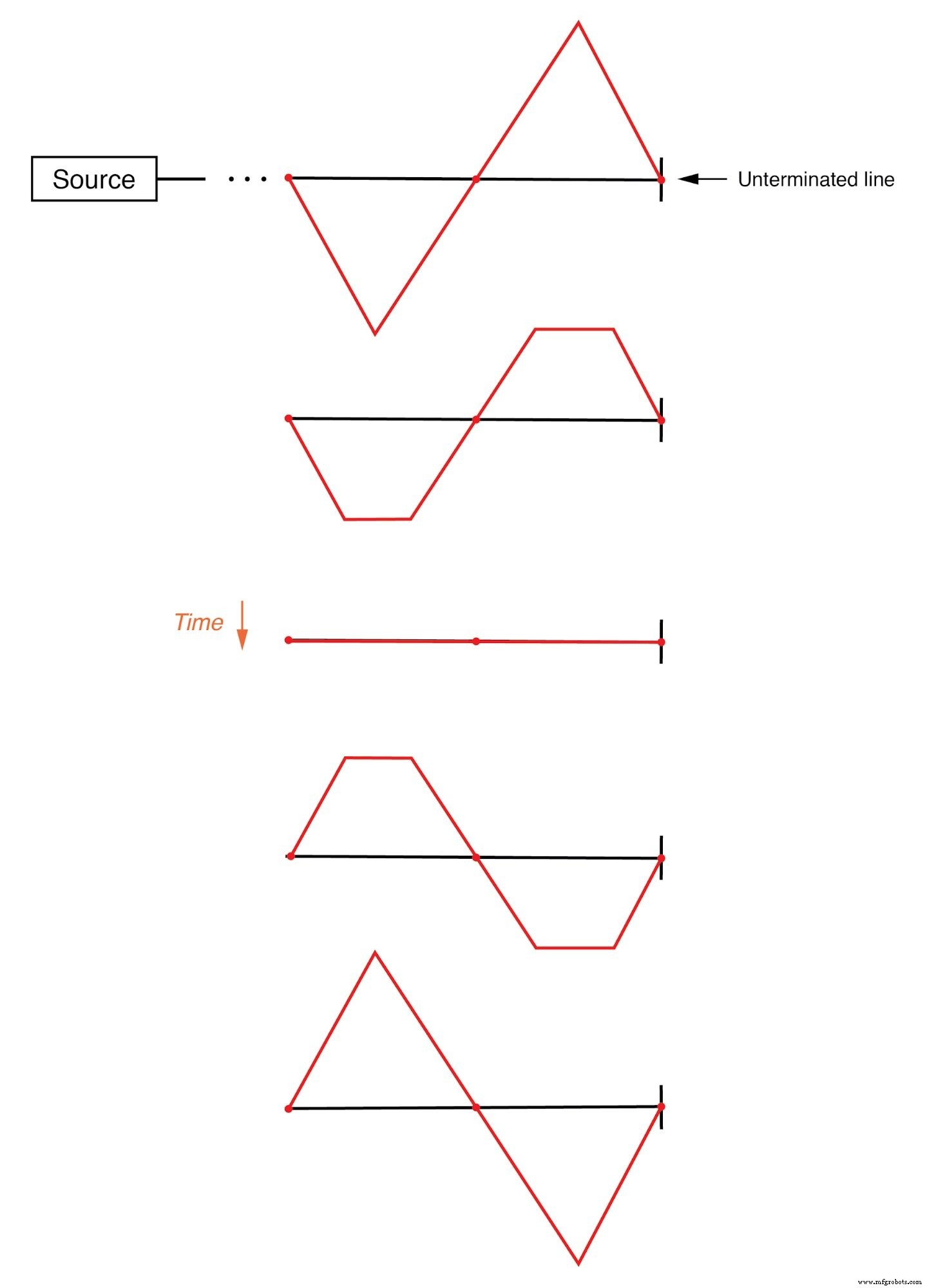
定在波は伝送線路に沿って伝播しません。

定在波が発生する場合

実世界では定在波が非常に豊富です。ひもまたはロープを考えてみましょう。一方の端を振って、もう一方の端を縛ります（手の動きの半サイクルだけが示され、下に移動します）:(下の図）

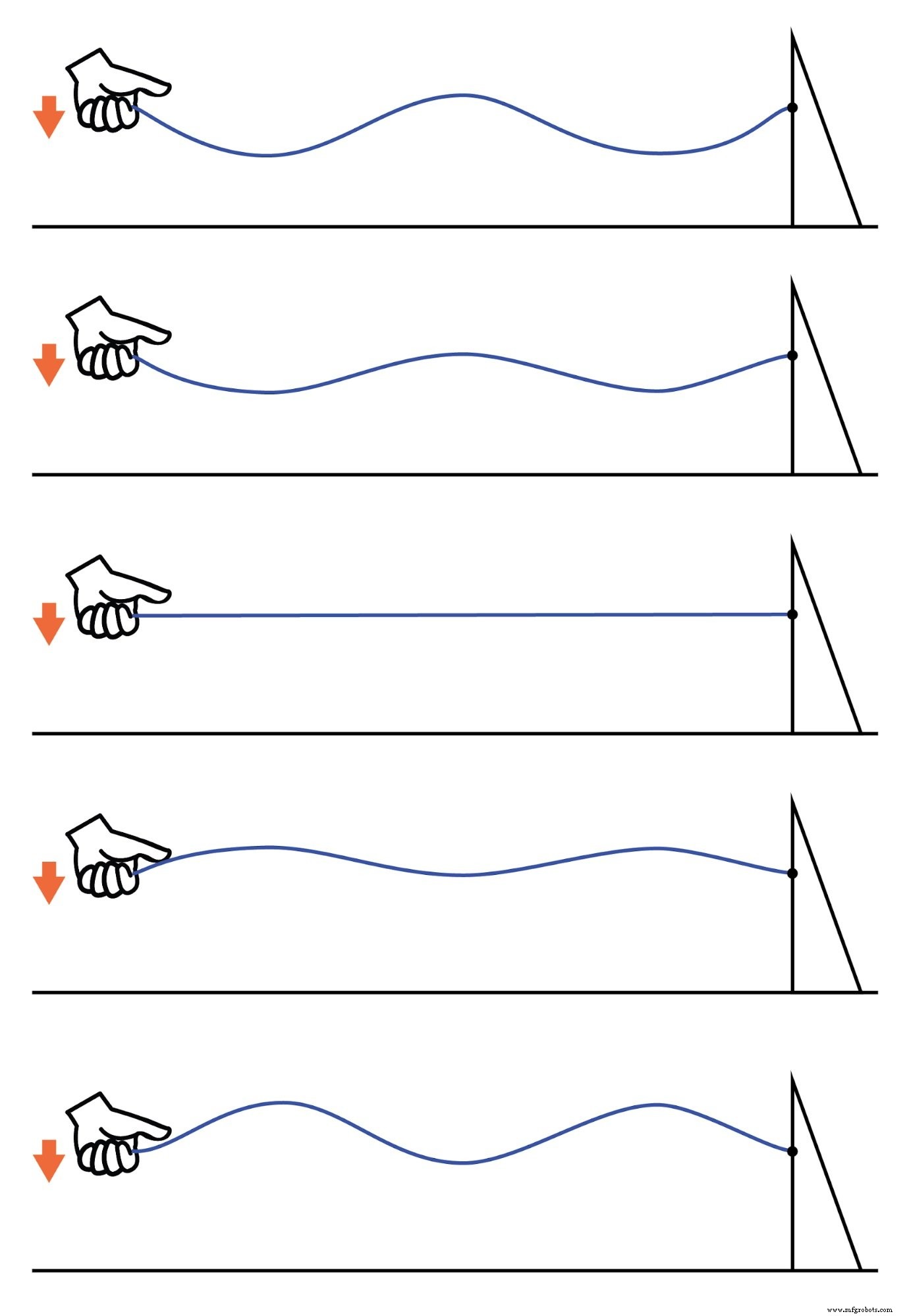
ロープに定在波。

節（振動がほとんどまたはまったくない点）と波腹（最大振動の点）の両方が、弦またはロープの長さに沿って固定されたままです。

この効果は、自由端を適切な周波数で振ったときに最も顕著になります。撥弦楽器は同じ「定在波」の振る舞いを示し、その長さに沿って最大および最小の振動の「ノード」があります。

撥弦楽器と撥弦楽器の主な違いは、撥弦楽器が独自の「正しい」振動周波数を供給して、定在波効果を最大化することです。（下の図）

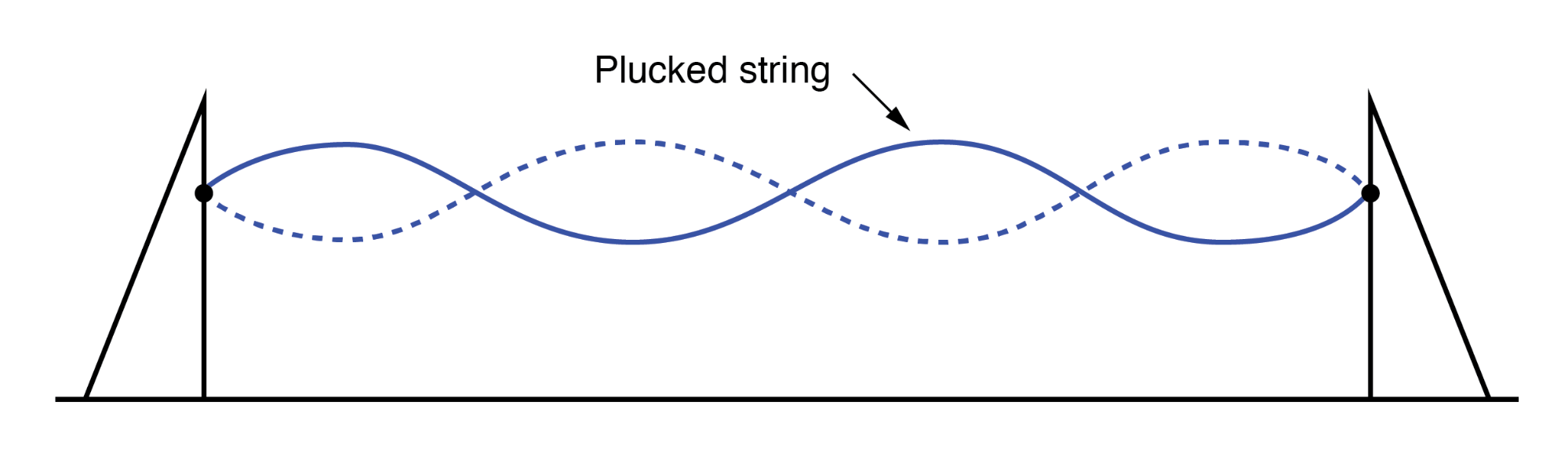
撥弦楽器の定在波。

オープンエンドのチューブを横切って吹く風も定在波を生成します。今回の波は、固体の振動ではなく、管内の空気分子（音）の振動です。定在波がノード（最小振幅）で終了するか、波腹（最大振幅）で終了するかは、チューブのもう一方の端が開いているか閉じているかによって異なります:(下の図）

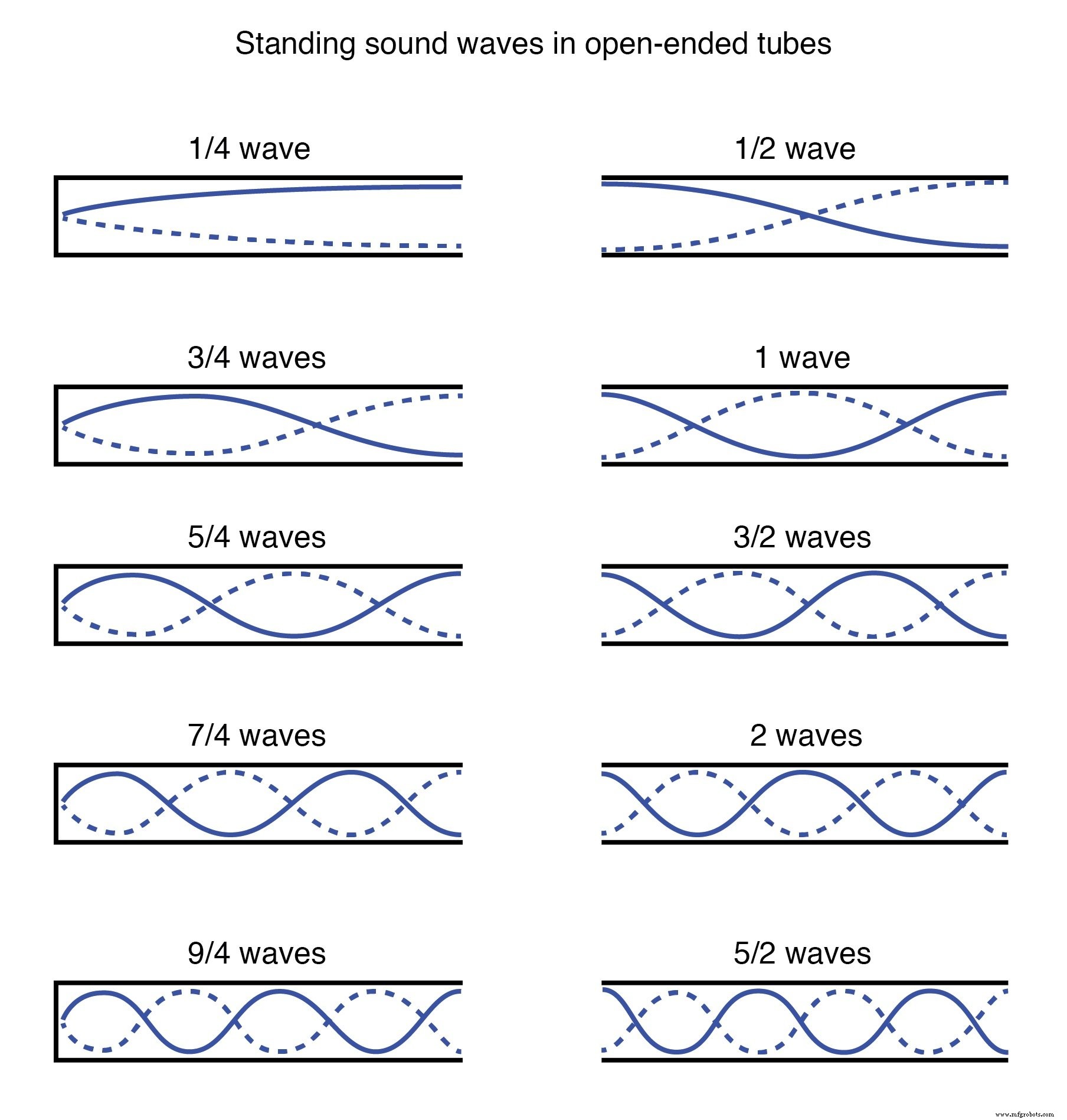
オープンエンドのチューブに音波を立てます。

閉じたチューブの端は波の節である必要があり、開いたチューブの端は波の節である必要があります。類推すると、振動する弦の固定された端は節である必要があり、自由端（存在する場合）は波腹である必要があります。

共振周波数の高調波の進行

チューブの終点に正確に一致する、チューブ内の振動する空気の定在波を生成するのに適した波長が複数あることに注意してください。

これは、すべての定在波システムに当てはまります。定在波は、システムのノード/波腹点に相関する任意の周波数（波長）でシステムと共振します。別の言い方をすれば、定在波をサポートするシステムには複数の共振周波数があるということです。

すべてのより高い周波数は、システムの最低（基本）周波数の整数倍です。ある共振周波数から次の共振周波数への高調波の連続的な進行により、倍音が定義されます。 システムの周波数:(下の図）

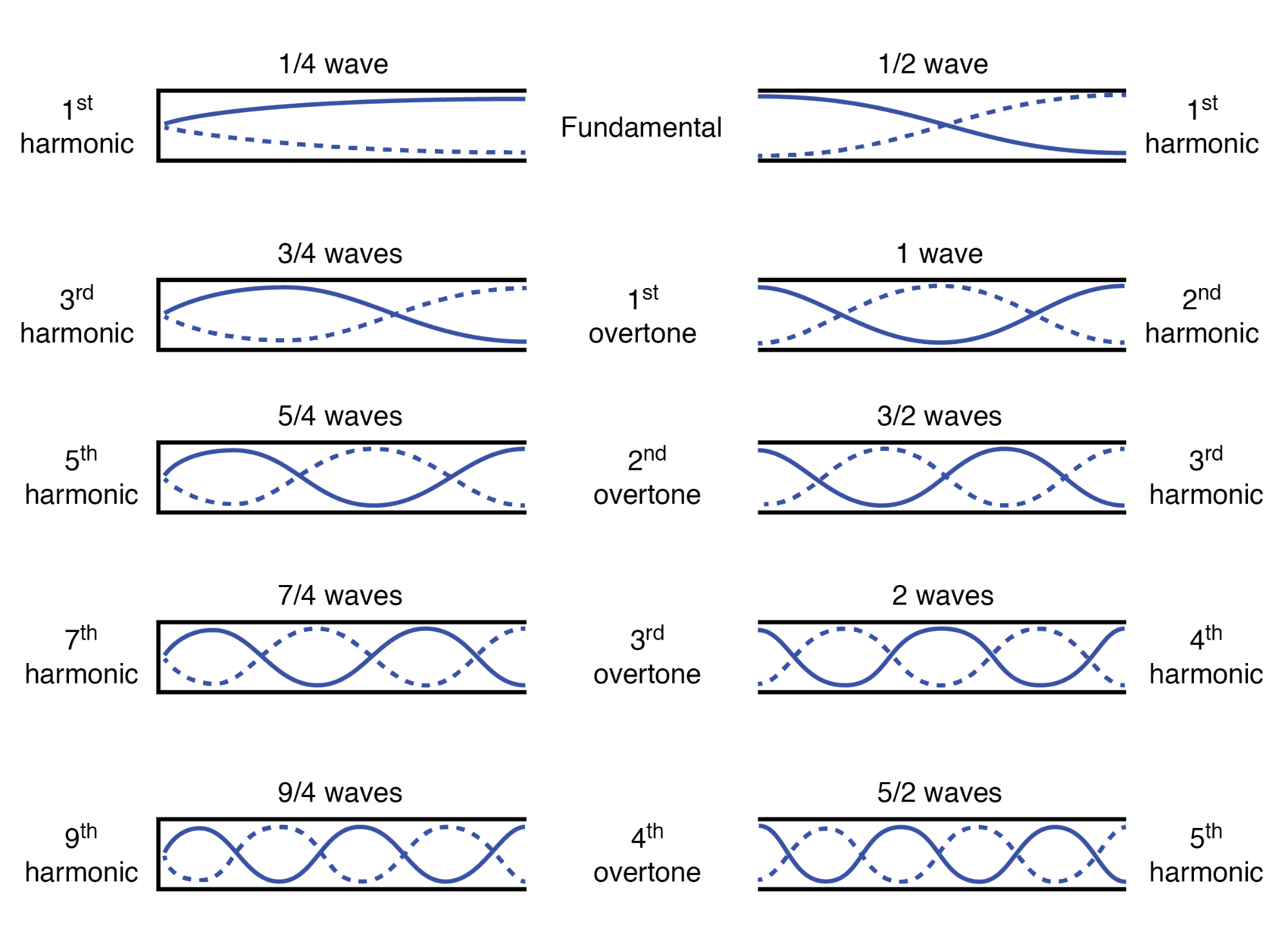
オープンエンドパイプのハーモニクス（倍音）

これらの倍音または倍音の実際の周波数（ヘルツで測定）は、チューブの物理的な長さと、空気中の音速である波の伝播速度によって異なります。

SPICEを使用した伝送線路共振のシミュレーション

伝送線路は定在波をサポートし、これらの波に負荷端の終端インピーダンスのタイプに応じてノードと波腹を持たせるため、物理的な長さと伝搬速度によって決定される周波数でも共振を示します。

ただし、伝送線路の共振は、電圧波と電流波の両方を考慮する必要があるため、ストリングやチューブ内の空気の共振よりも少し複雑です。

この複雑さは、コンピューターシミュレーションによって理解しやすくなります。まず、完全に一致するソース、伝送ライン、および負荷を調べてみましょう。すべてのコンポーネントのインピーダンスは75Ωです:(下の図）

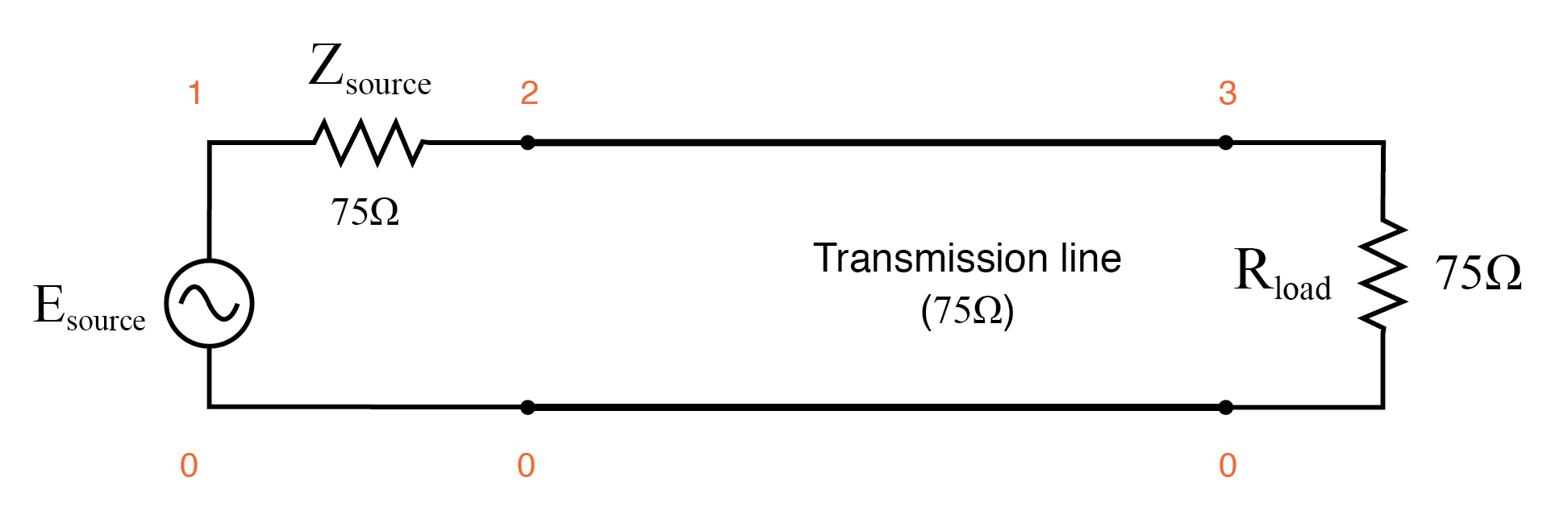
完全に一致する伝送線路。

SPICEを使用して回路をシミュレートし、伝送線路（ t1 ）を指定します ）75Ωの特性インピーダンス（ z0 =75 ）および1マイクロ秒の伝搬遅延（ td =1u ）。これは、伝送線路の物理的な長さ、つまり波がその全長を伝播するのにかかる時間を表すための便利な方法です。

これが実際の75Ωケーブル（おそらくケーブルテレビ配信に一般的に使用されるタイプの「RG-59B / U」同軸ケーブル）で、速度係数が0.66の場合、長さは約648フィートになります。

1 µsは1 MHz信号の周期であるため、AC電源の周波数を（ほぼ）ゼロからその数値までスイープして、DCから1波長の範囲の信号にさらされたときにシステムがどのように反応するかを確認します。

上記の回路のSPICEネットリストは次のとおりです。

送電線 v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 =75 td =1u rload 3 0 75 .ac lin 101 1m 1meg *「ナツメグ」プログラムを使用して分析をプロットする 。終わり 

このシミュレーションを実行し、ソースインピーダンスドロップ（電流の指標として）、ソース電圧、ラインのソースエンド電圧、および負荷電圧をプロットすると、ソース電圧がvm（1）（電圧の大きさグラフィックプロット上のノード1とノード0の暗黙の接地点-安定した1ボルトを記録し、他のすべての電圧は安定した0.5ボルトを記録します:(下の図）

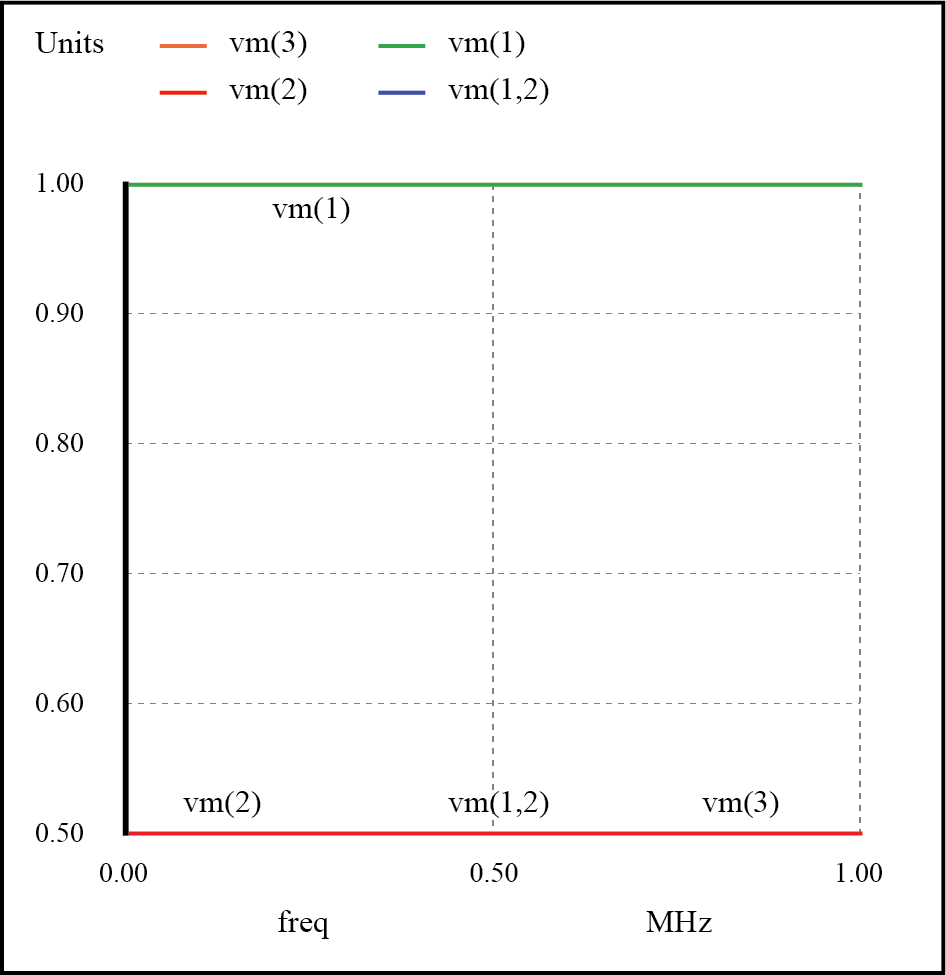
一致した伝送ラインに共振はありません。

すべてのインピーダンスが完全に一致しているシステムでは、定在波が存在しない可能性があるため、ボード線図に共振する「ピーク」または「谷」はありません。

次に、負荷インピーダンスを999MΩに変更して、オープンエンドの伝送ラインをシミュレートしましょう。 （下の図）周波数が1mHzから1MHzに掃引されると、ライン上にいくつかの反射が確実に見られるはずです:(下の図）

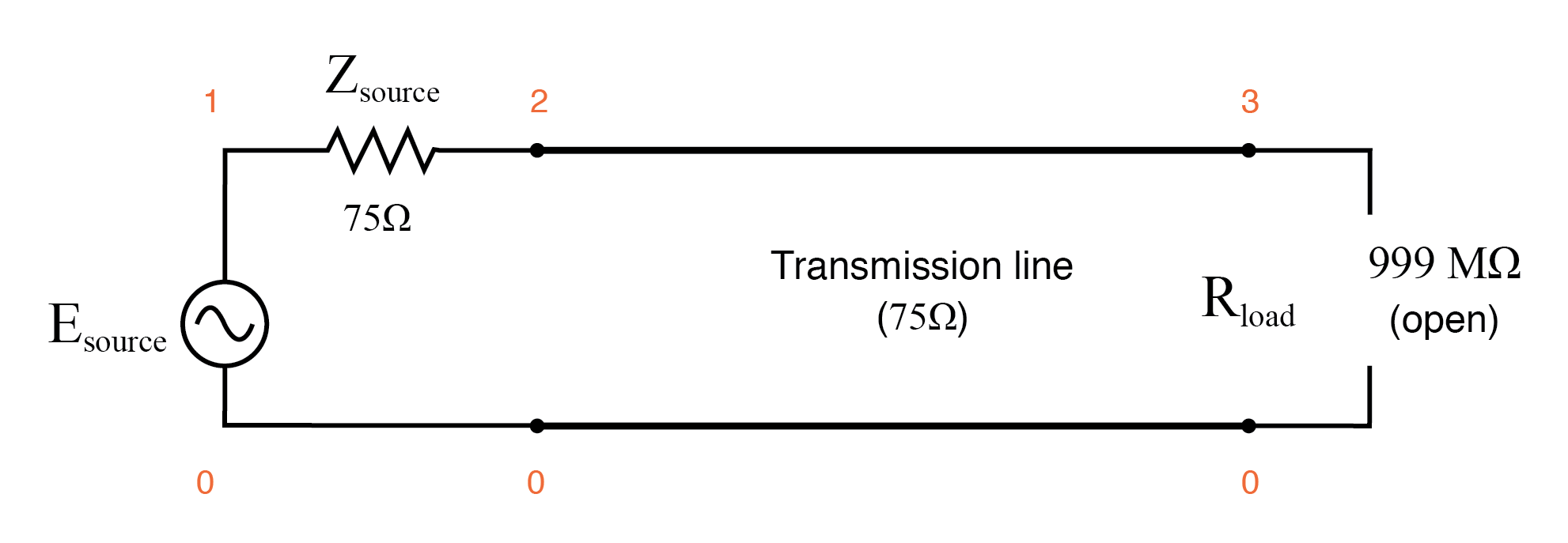
オープンエンドの伝送ライン。

送電線 v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 =75 td =1u rload 3 0 999meg .ac lin 101 1m 1meg *「ナツメグ」プログラムを使用して分析をプロットする 。終わり 

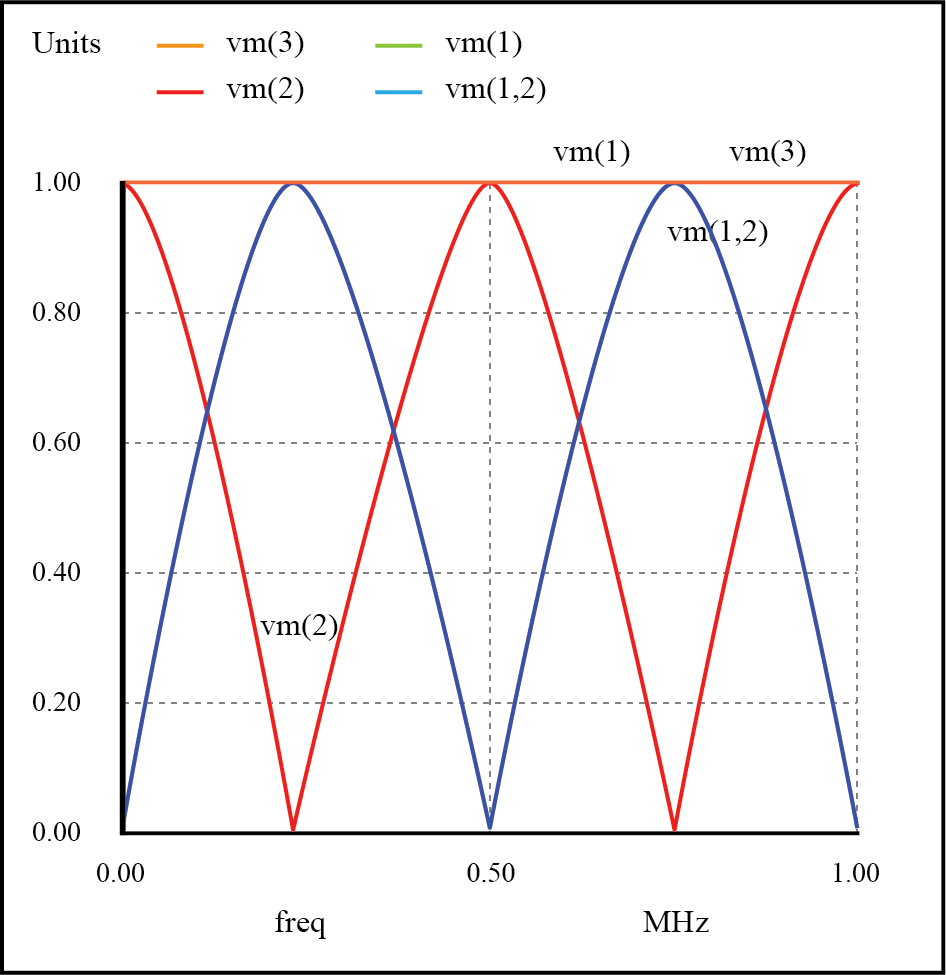
開いている伝送線路の共振。

ここでは、両方の供給電圧 vm（1） およびラインの負荷端電圧 vm（3） 1ボルトで安定したままです。他の電圧は、1 mHz〜1MHzの掃引範囲に沿ってさまざまな周波数でディップおよびピークになります。

分析の横軸に沿って、0 Hz、250 kHz、500 kHz、750 kHz、および1MHzの5つの注目点があります。回路のさまざまなポイントでの電圧と電流に関して、それぞれを調査します。

0 Hz（実際には1 mHz）では、信号は実質的にDCであり、回路は1ボルトのDCバッテリーソースを使用した場合とほぼ同じように動作します。

ソースインピーダンス（Z _ソース）でのゼロ電圧降下によって示されるように、回路電流はありません。 ： vm（1,2） ）、および伝送ラインのソース端に存在する完全なソース電圧（ノード2とノード0の間で測定された電圧： vm（2） ）。 （下の図）

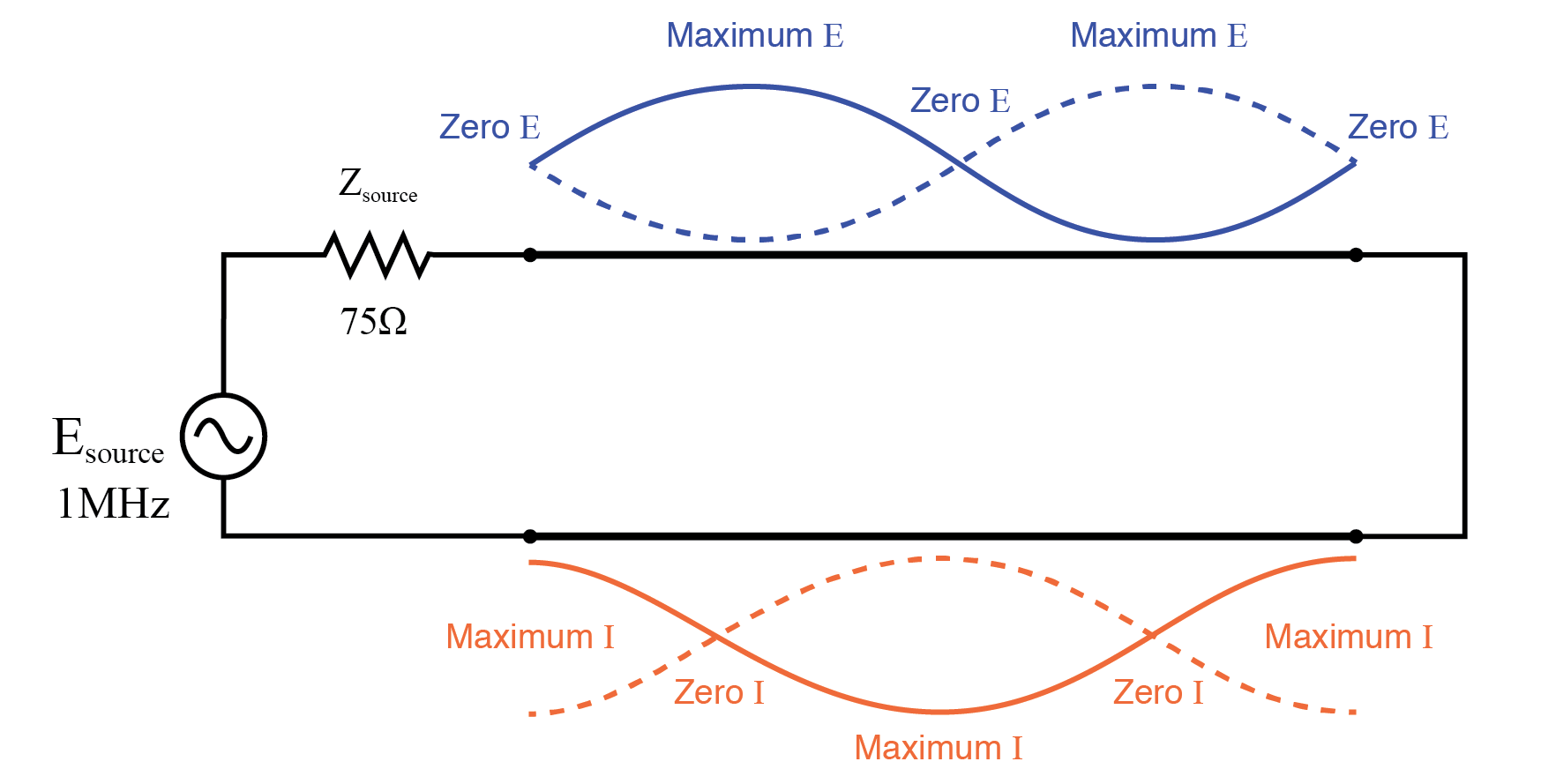
f =0の場合：入力：V =1、I =0;終了：V =1、I =0。

250 kHzでは、送電線のソース側でゼロ電圧と最大電流が見られますが、負荷側ではまだフル電圧です:(下の図）

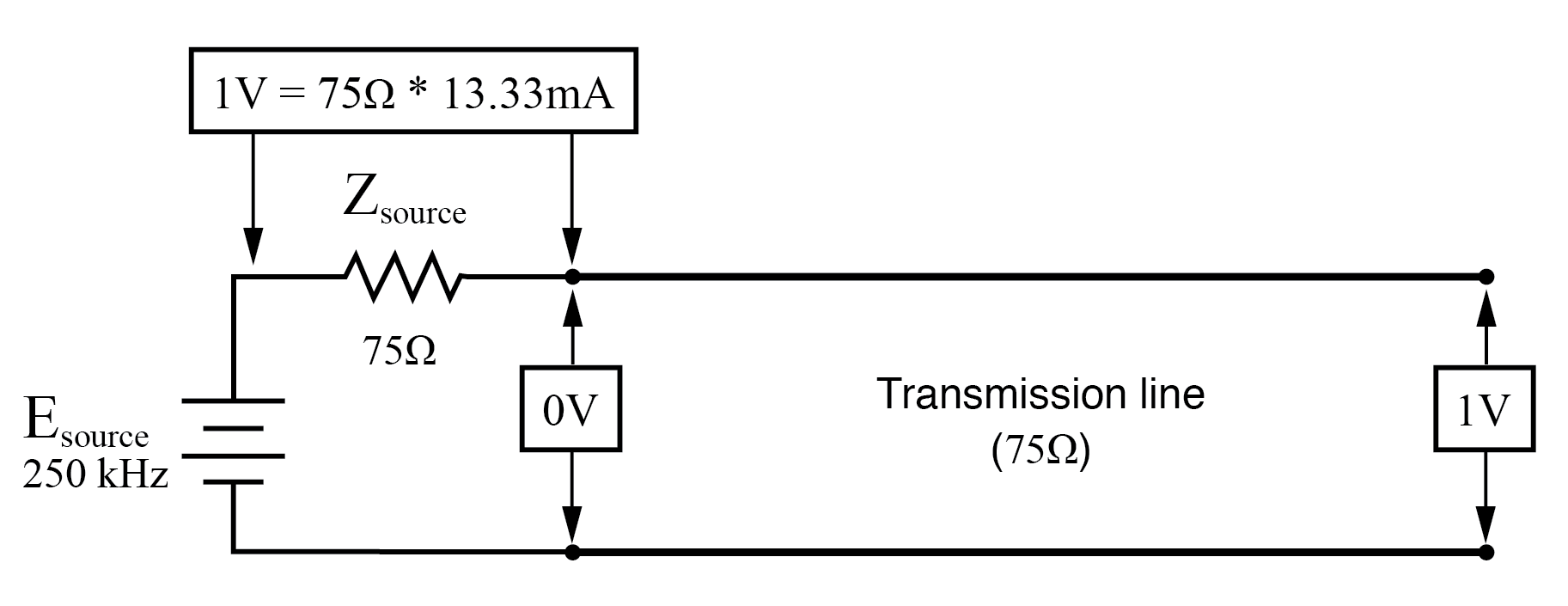
f =250 KHzの場合：入力：V =0、I =13.33 mA;終了：V =1 I =0。

あなたは疑問に思うかもしれません、これはどうしてですか？入口に電圧がゼロのときに、ラインの開放端で完全な電源電圧を取得するにはどうすればよいですか？

その答えは、定在波のパラドックスにあります。ソース周波数が250kHzの場合、ラインの長さは1/4波長が端から端までぴったり合うように正確に調整されます。ラインの負荷端が開いていると、電流は流れませんが、電圧は流れます。

したがって、開回路送電線の負荷端は、電流ノード（ゼロ点）と電圧波腹（最大振幅）です:(下の図）

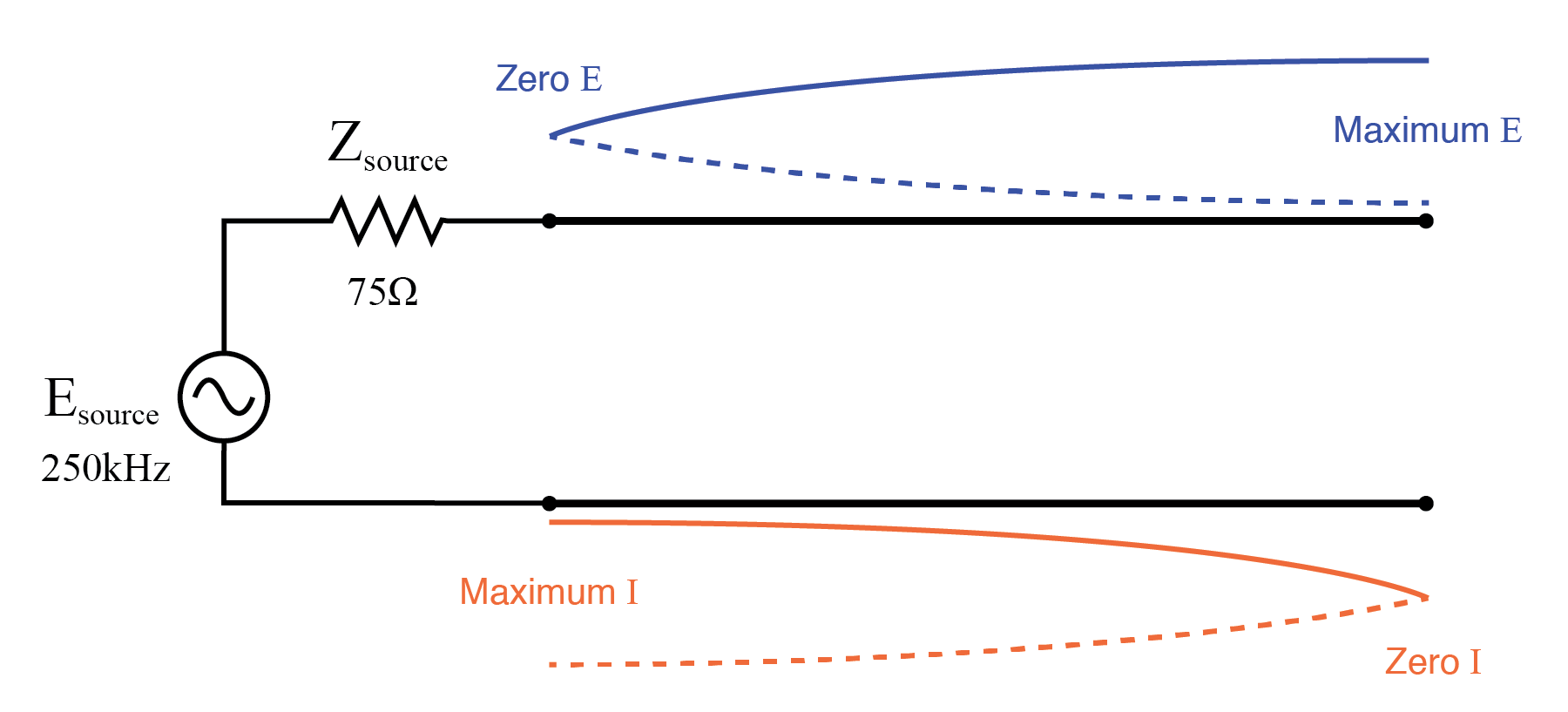
送電線の開放端には、現在のノード、開放端の電圧波腹が表示されます。

500 kHzでは、定在波のちょうど半分が伝送線路上にあります。ここで、ソース電流がゼロに低下し、伝送線路のソース端電圧が再び最大電圧に上昇する分析の別のポイントがわかります。 ：(下の図）

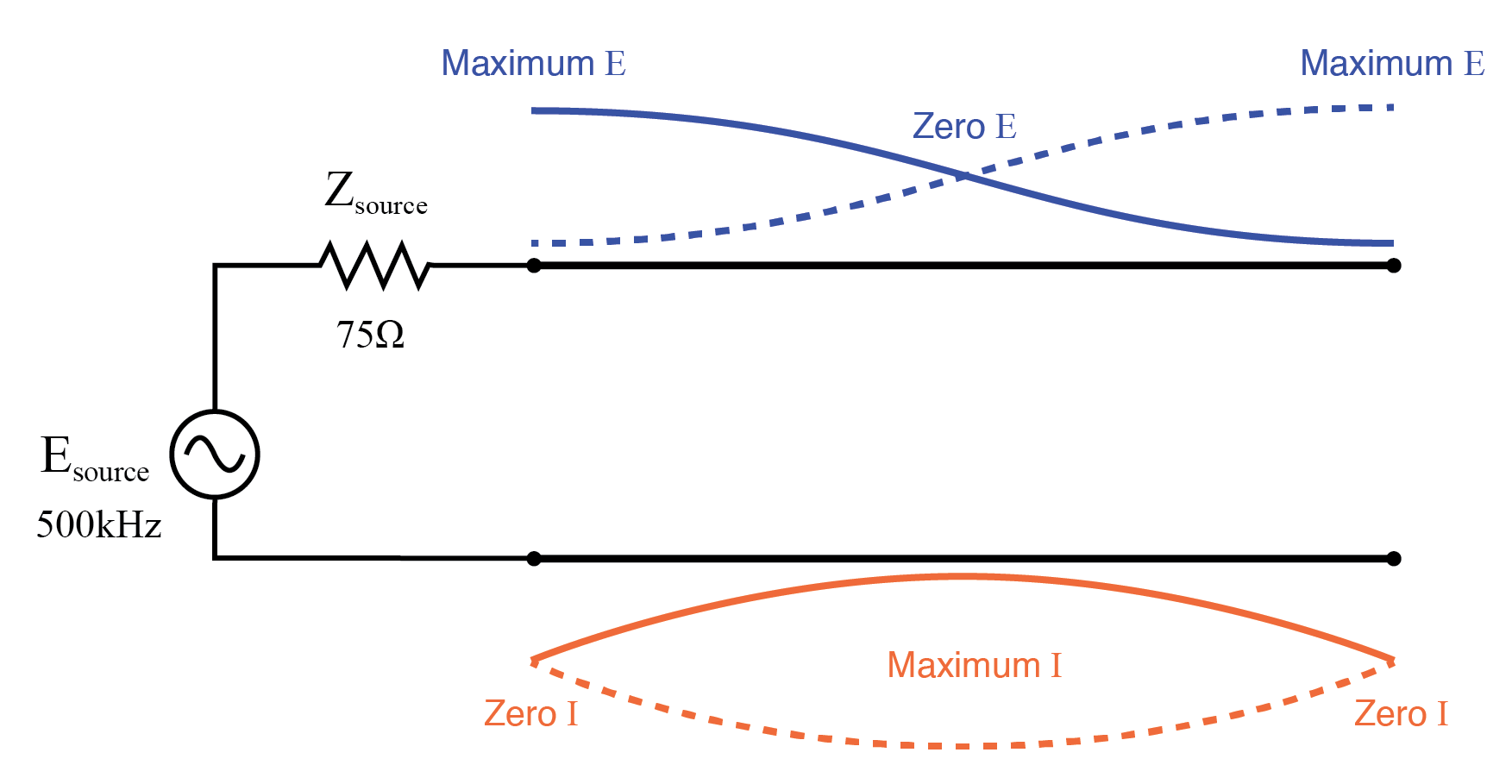
半波開放伝送線路上の完全定在波。

750 kHzでは、プロットは250 kHzの場合とよく似ています。つまり、ゼロソースエンド電圧（vm（2））と最大電流（vm（1,2））です。これは、伝送線路に沿って波の3/4が発生し、伝送線路のもう一方の端が開回路であっても、伝送線路に接続する場所でソースが短絡を「認識」するためです。（図以下）

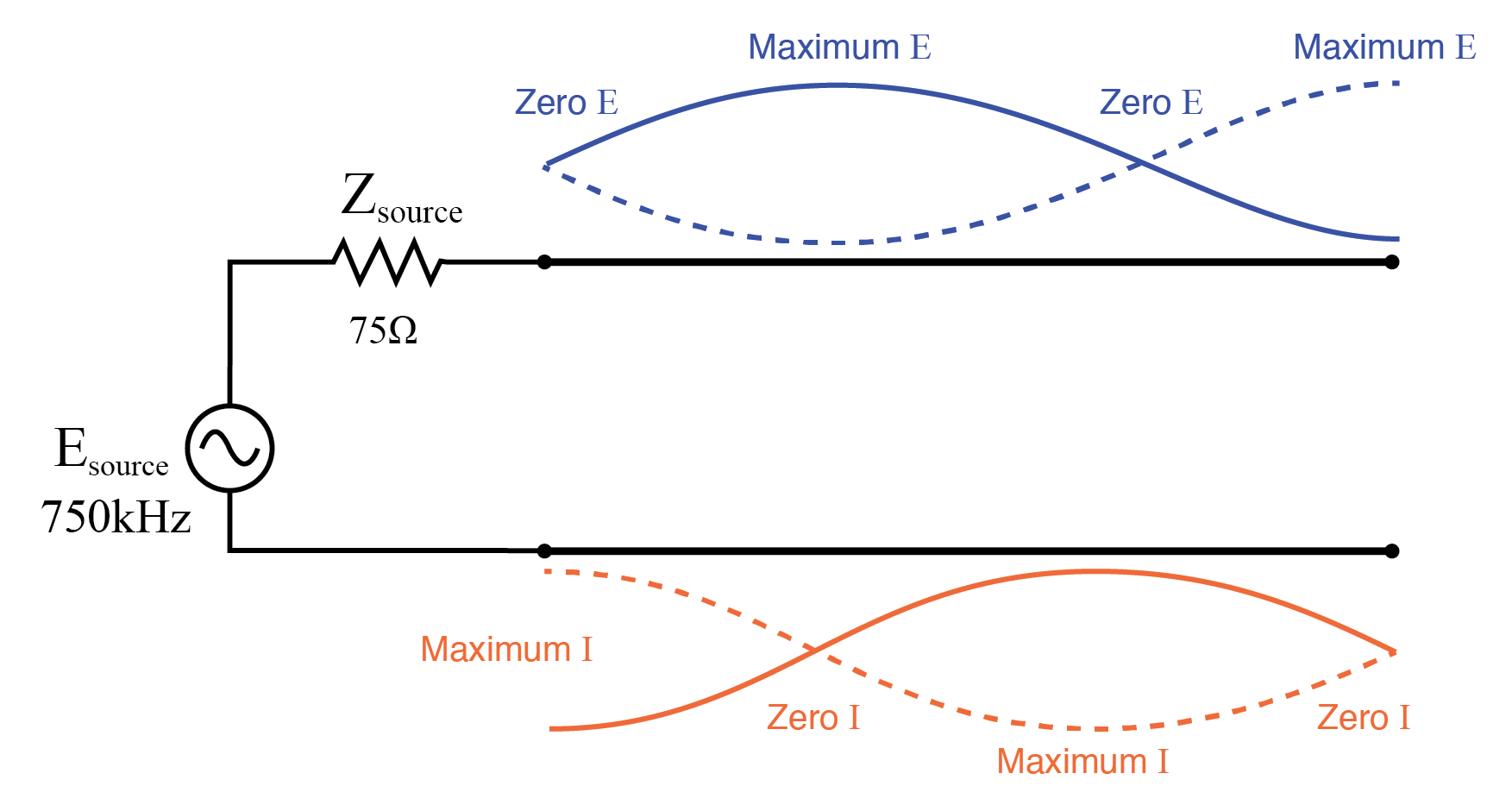
3/4波のオープン伝送ライン上の11/2の定在波。

供給周波数が最大1MHzまで掃引されると、伝送線路上に完全な定在波が存在します。この時点で、ラインのソース側は負荷側と同じ電圧と電流の振幅、つまり全電圧とゼロ電流を経験します。本質的に、ソースは、伝送ラインに接続するポイントで開回路を「認識」します。 （下の図）

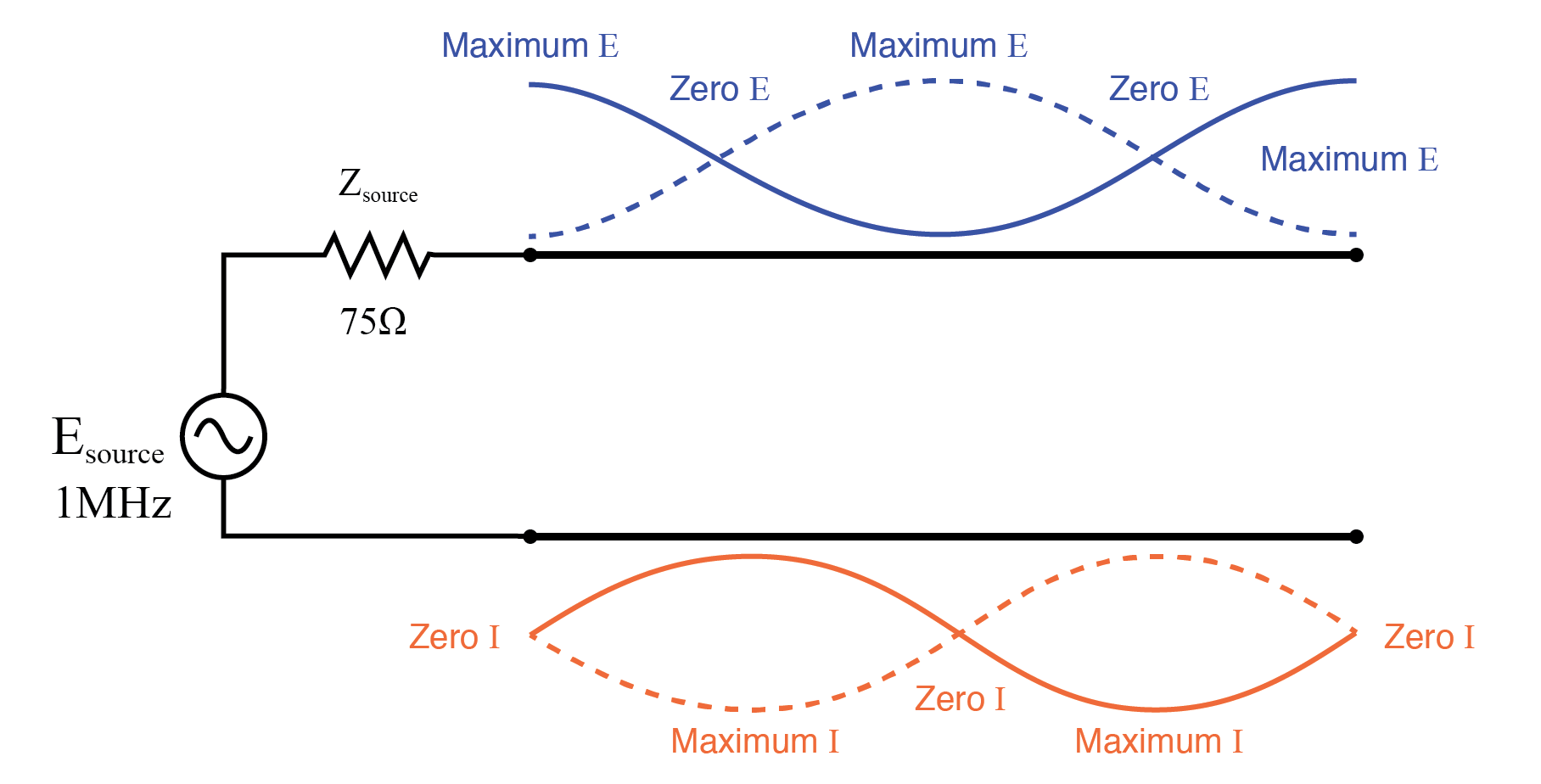
全波開放伝送線路上の二重定在波。

同様に、短絡した送電線は定在波を生成しますが、電圧と電流のノードと波腹の割り当ては逆になります。線の短絡端では、電圧（ノード）と最大電流（腹）がゼロになります。 。以下は、SPICEシミュレーションと、すべての興味深い周波数（0 Hz、250 kHz、500 kHz、750 kHz、および1 MHz）で何が起こるかを示しています。短絡ジャンパーは、1 µΩの負荷インピーダンスでシミュレートされます。

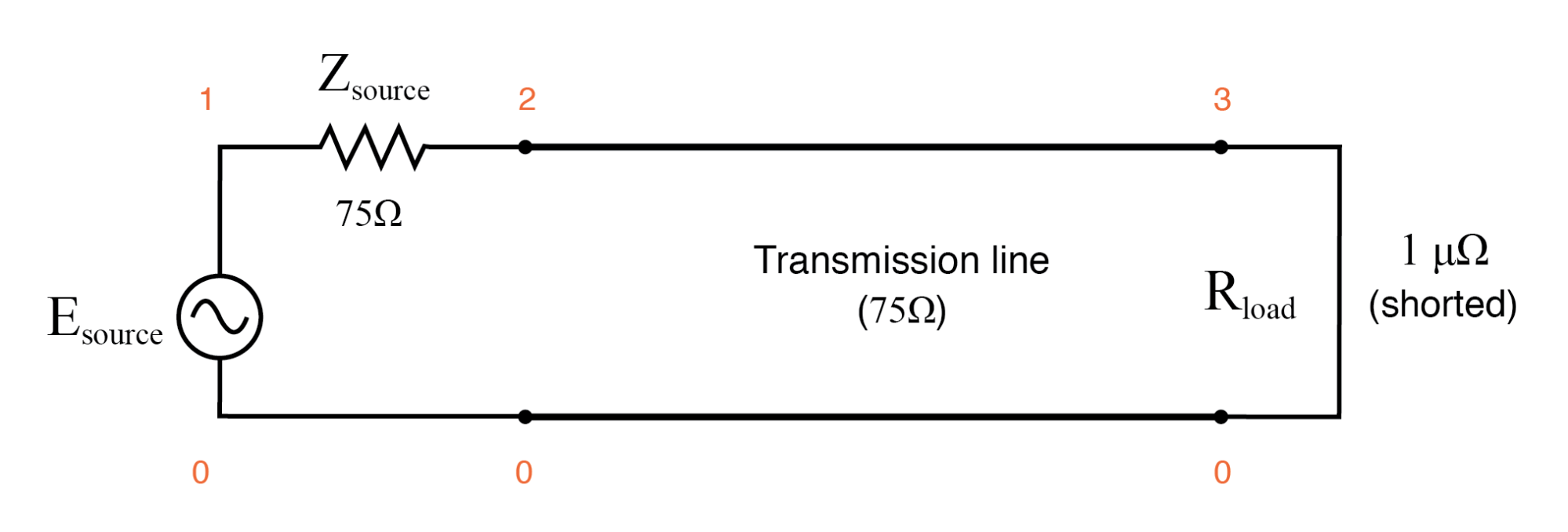
短い伝送線路。

送電線 v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 =75 td =1u rload 3 0 1u .ac lin 101 1m 1meg *「ナツメグ」プログラムを使用して分析をプロットする 。終わり 

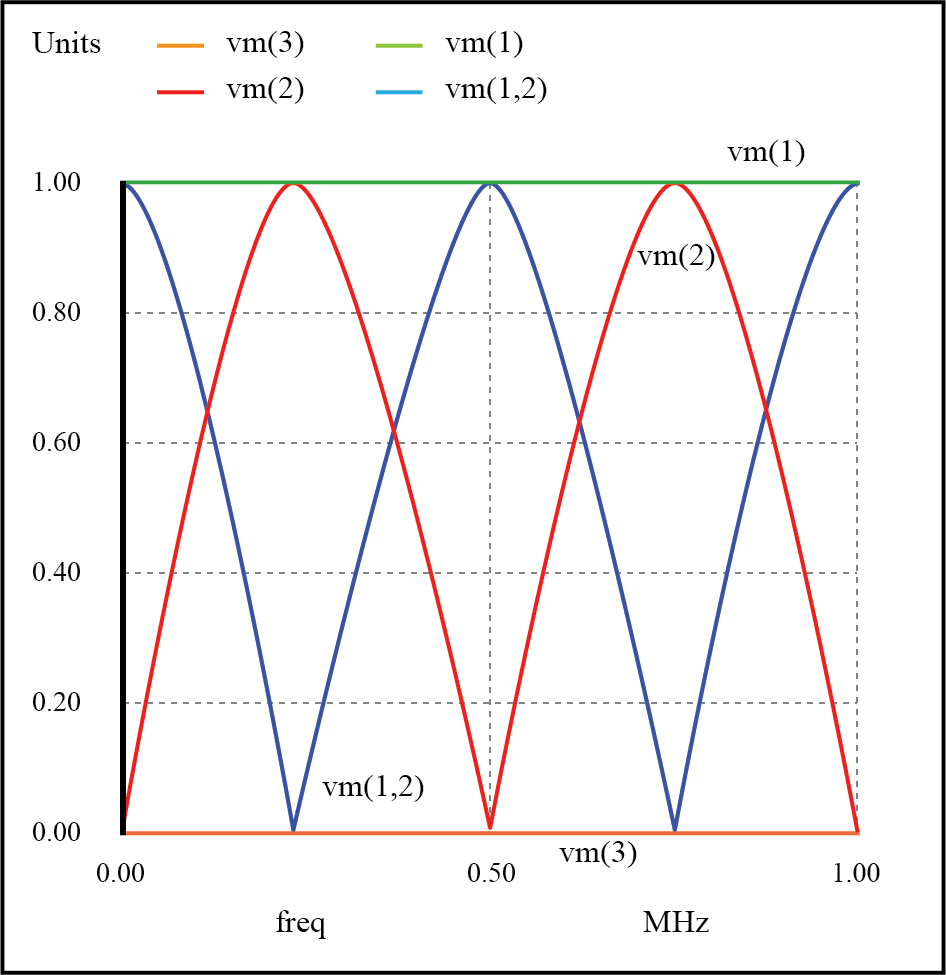
短絡した伝送線路の共振

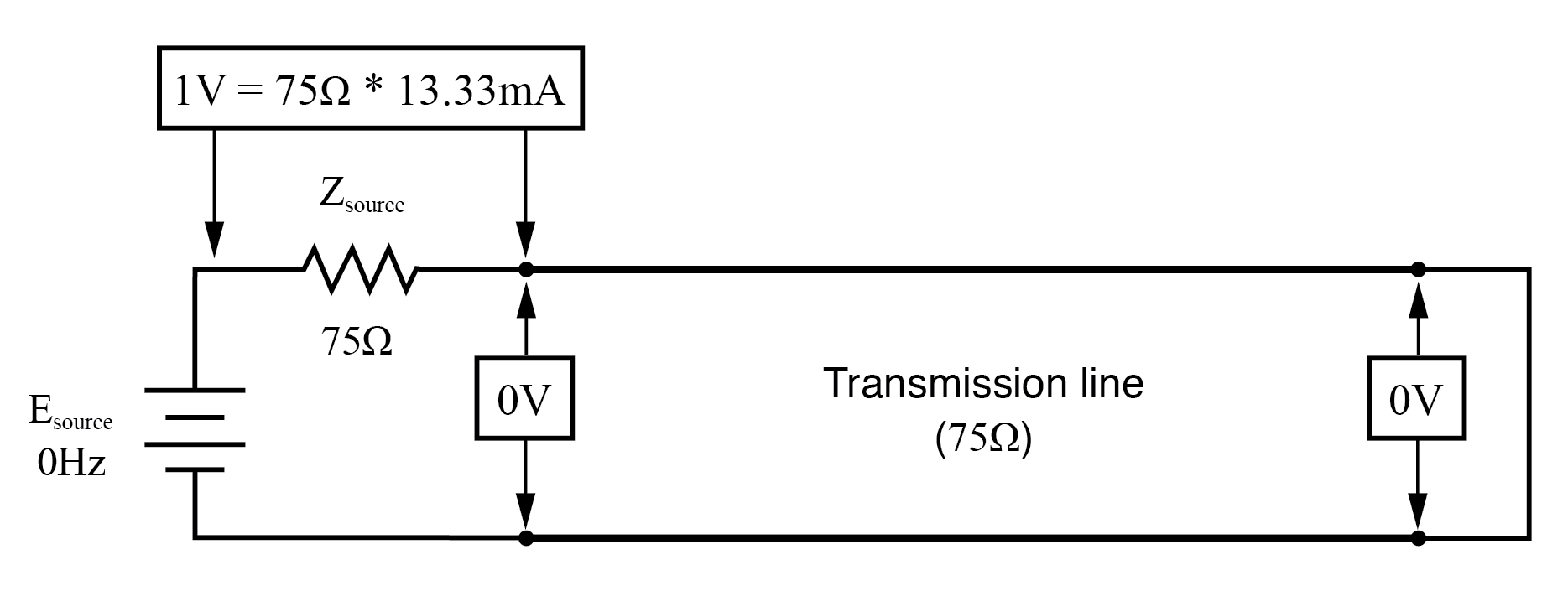
f =0 Hzの場合：入力：V =0、I =13.33 mA;終了：V =0、I =13.33mA。

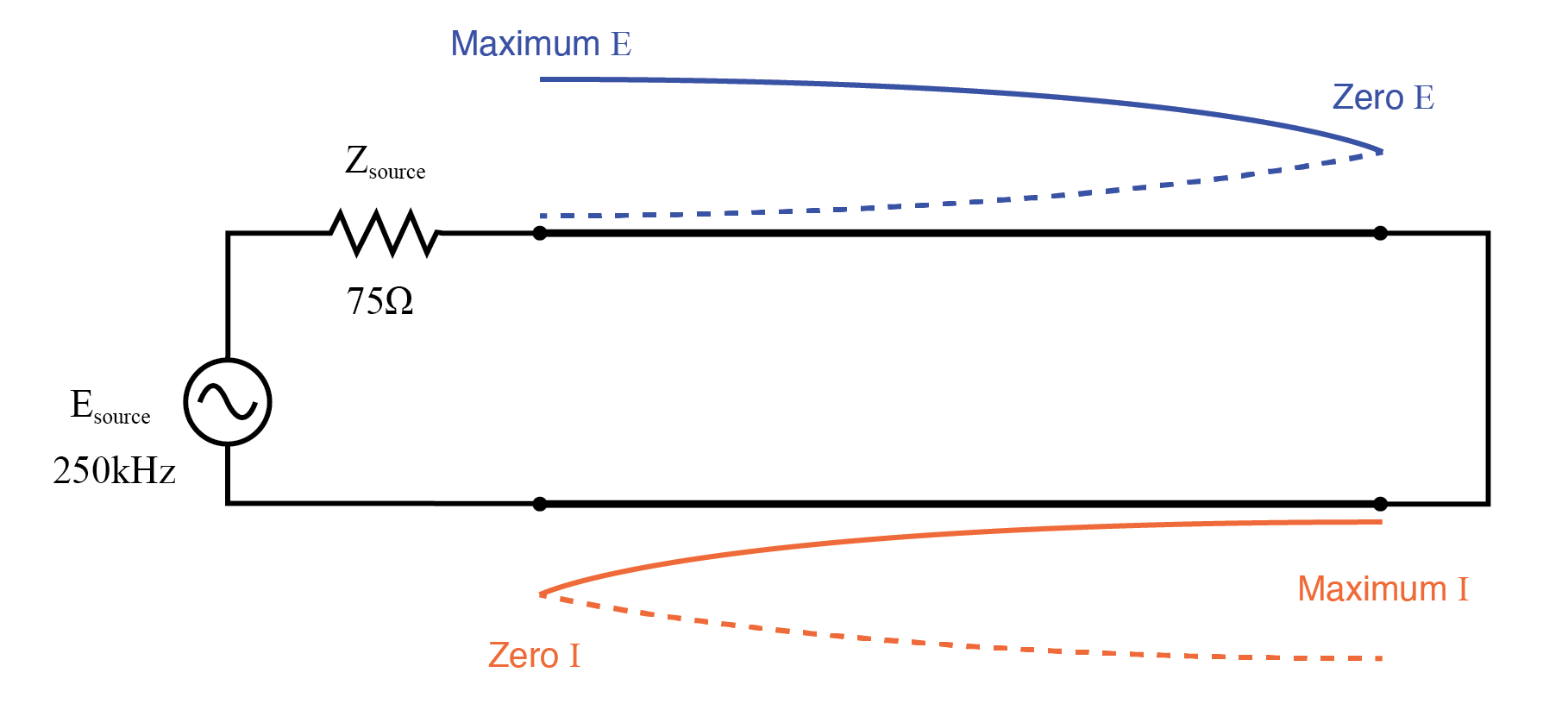
1/4波長短絡伝送線路の半波定在波パターン。

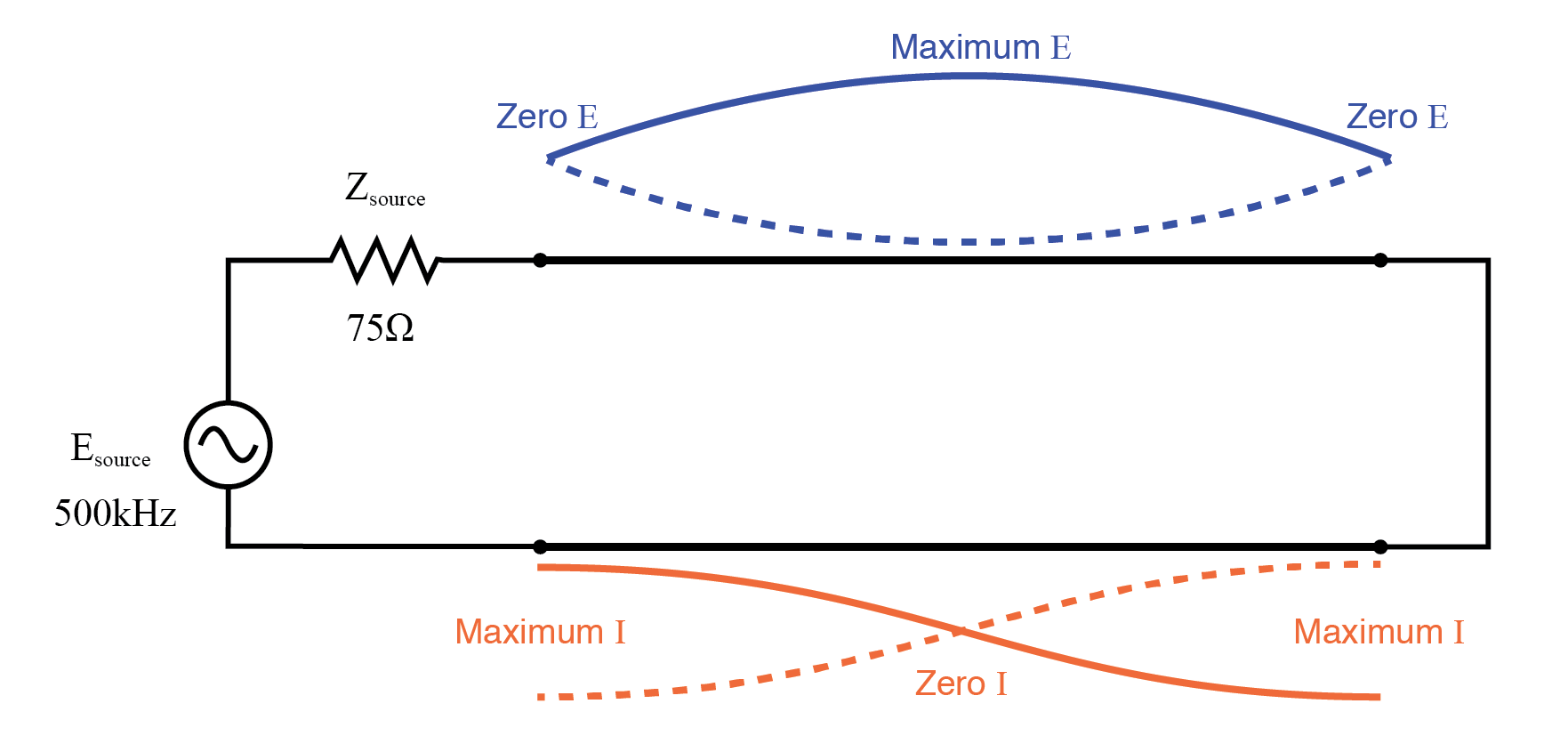
半波短絡伝送線路の全波定在波パターン。

3/4波短絡伝送線路上の11/2スタンディングウェーブパターン。

全波短絡伝送線路上の二重定在波。

開回路ラインと短絡ラインの両方の回路例では、エネルギー反射は合計です。ラインの端に到達する入射波の100％が反射されてソースに戻ります。

ただし、伝送ラインがオープンまたはショート以外のインピーダンスで終端されている場合、ラインに沿った電圧と電流の最小値と最大値の差と同様に、反射は弱くなります。

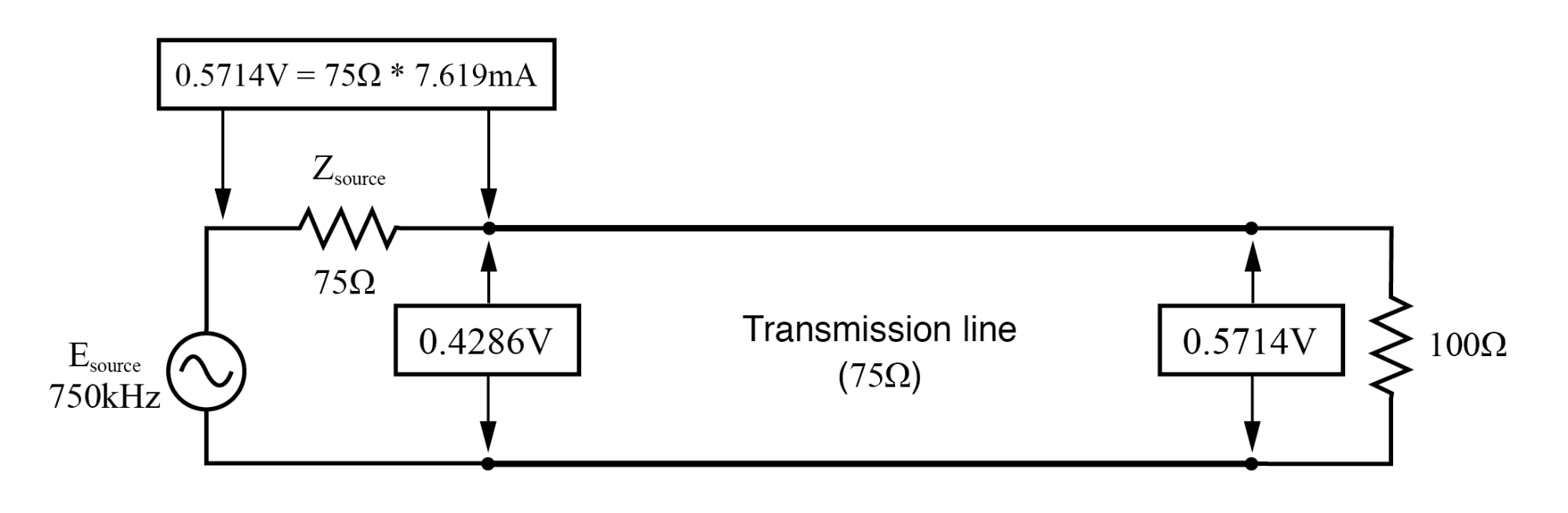
75Ωの抵抗ではなく100Ωの抵抗で例のラインを終端するとします。 （下の図）対応するSPICE分析の結果を調べて、さまざまなソース周波数でのインピーダンスの不一致の影響を確認します:(下の図）

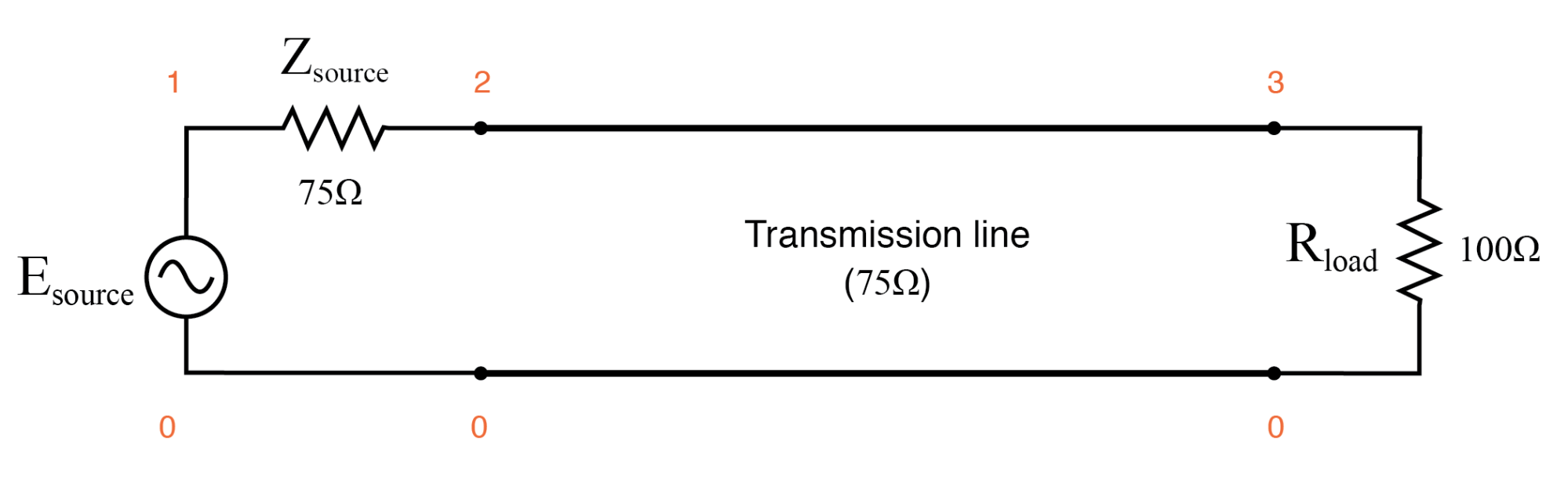
伝送線路が不一致で終了しました

送電線 v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 =75 td =1u rload 3 0100 .ac lin 101 1m 1meg *「ナツメグ」プログラムを使用して分析をプロットする 。終わり 

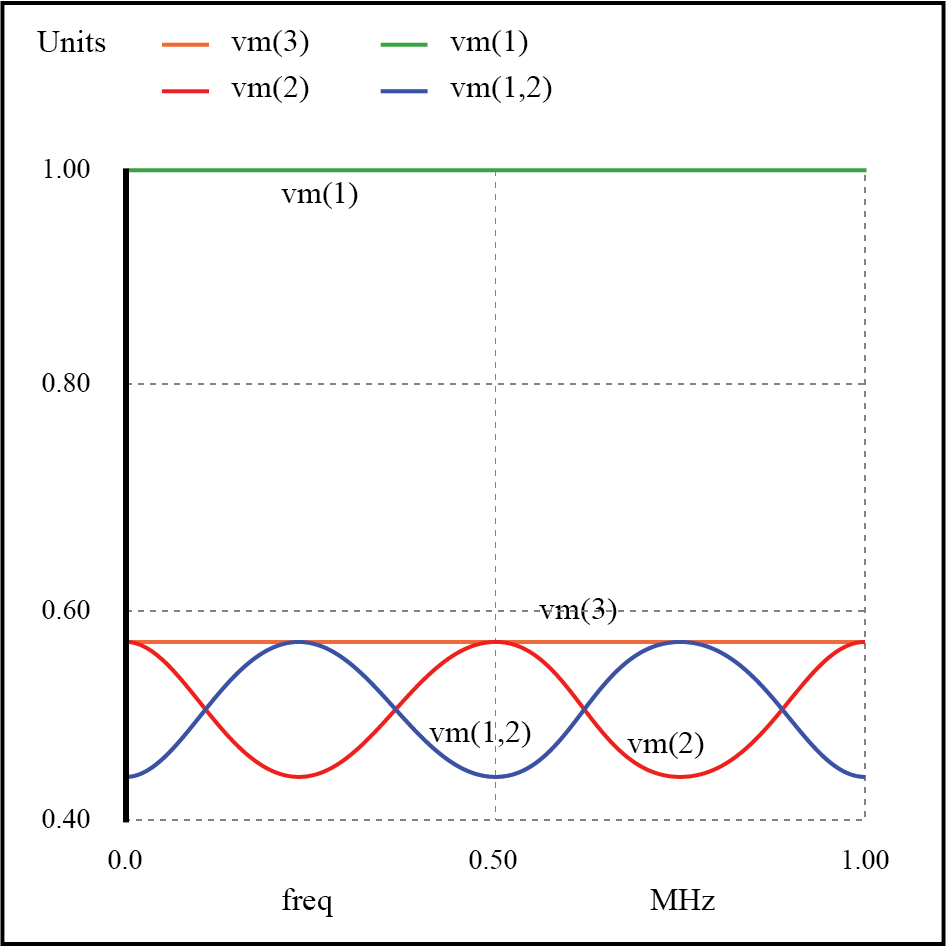
不一致の伝送線路での弱い共振

別のSPICE分析を実行すると、今回は数値結果をプロットするのではなく印刷することで、すべての興味深い周波数で何が起こっているかを正確に見つけることができます。

送電線 v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 =75 td =1u rload 3 0100 .ac lin 5 1m 1meg .print ac v（1,2）v（1）v（2）v（3） 。終わり 

 freq v（1,2）v（1）v（2）v（3） 1.000E-03 4.286E-01 1.000E + 00 5.714E-01 5.714E-01 2.500E + 05 5.714E-01 1.000E + 00 4.286E-01 5.714E-01 5.000E + 05 4.286E-01 1.000E + 00 5.714E-01 5.714E-01 7.500E + 05 5.714E-01 1.000E + 00 4.286E-01 5.714E-01 1.000E + 06 4.286E-01 1.000E + 00 5.714E-01 5.714E-01 

すべての周波数で、ソース電圧 v（1） 、必要に応じて、1ボルトで安定したままです。負荷電圧 v（3） 、も安定したままですが、より低い電圧：0.5714ボルトです。ただし、両方のライン入力電圧（ v（2） ）およびソースの75Ωインピーダンスで降下した電圧（ v（1,2） 、ソースから引き出される電流を示します）は周波数によって異なります。

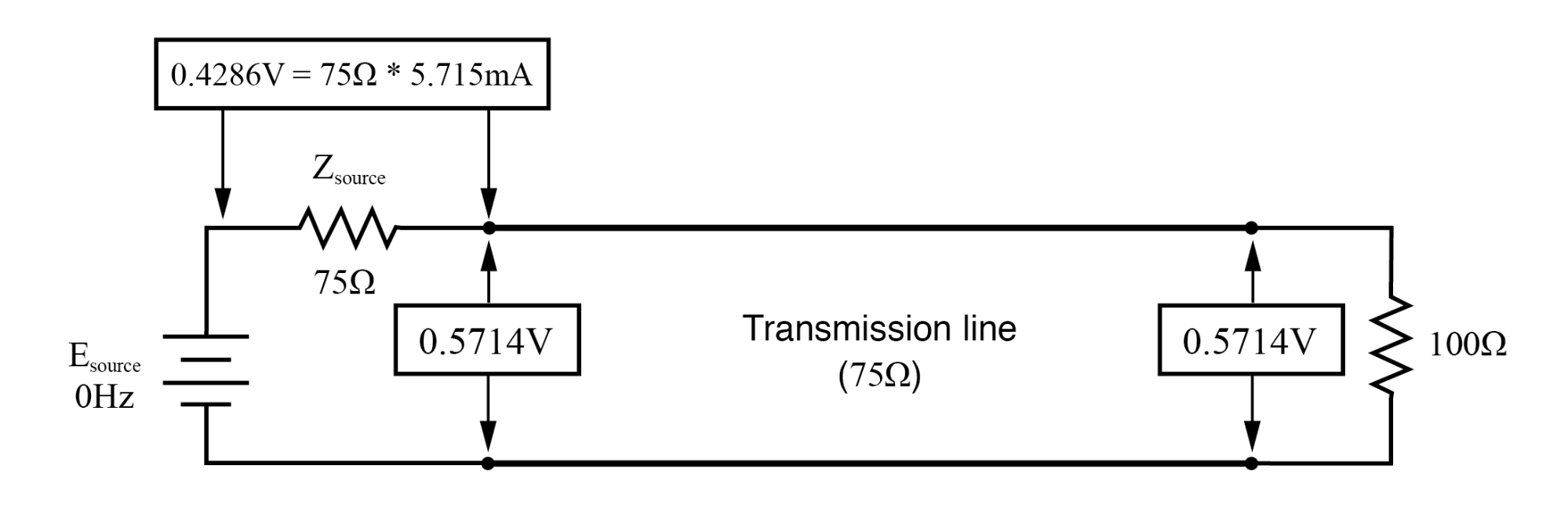
f =0 Hzの場合：入力：V =0.57.1​​4、I =5.715 mA;終了：V =0.5714、I =5.715mA。

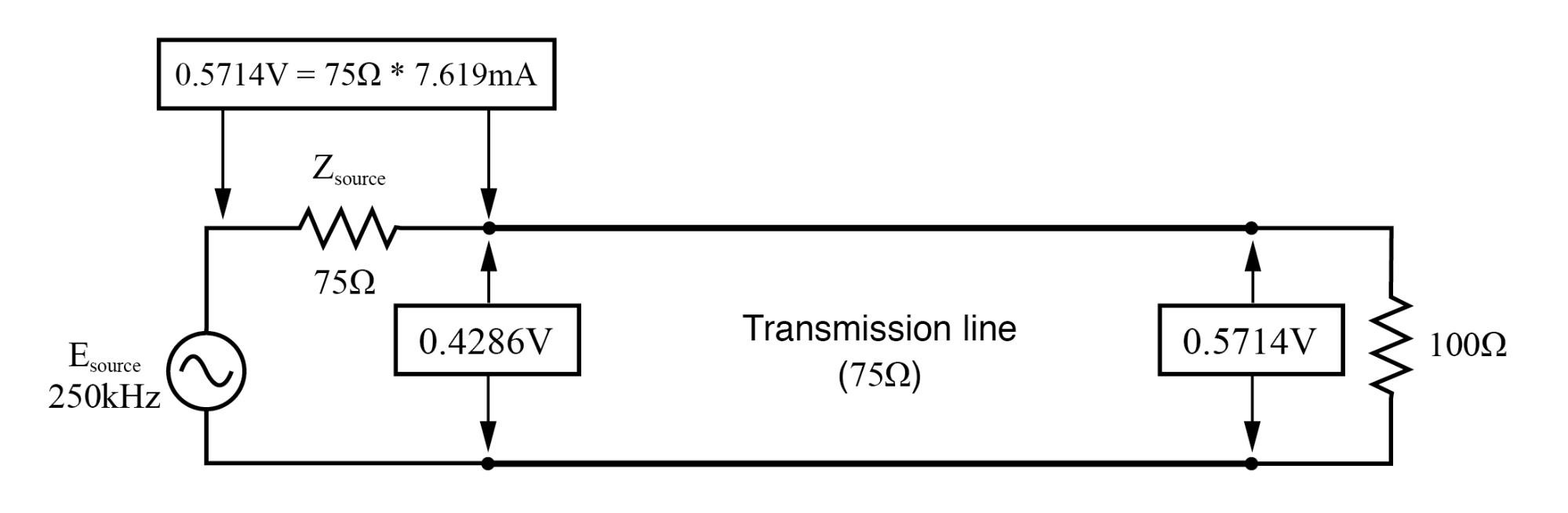
f =250 KHzの場合：入力：V =0.4286、I =7.619 mA;終了：V =0.5714、I =7.619mA。

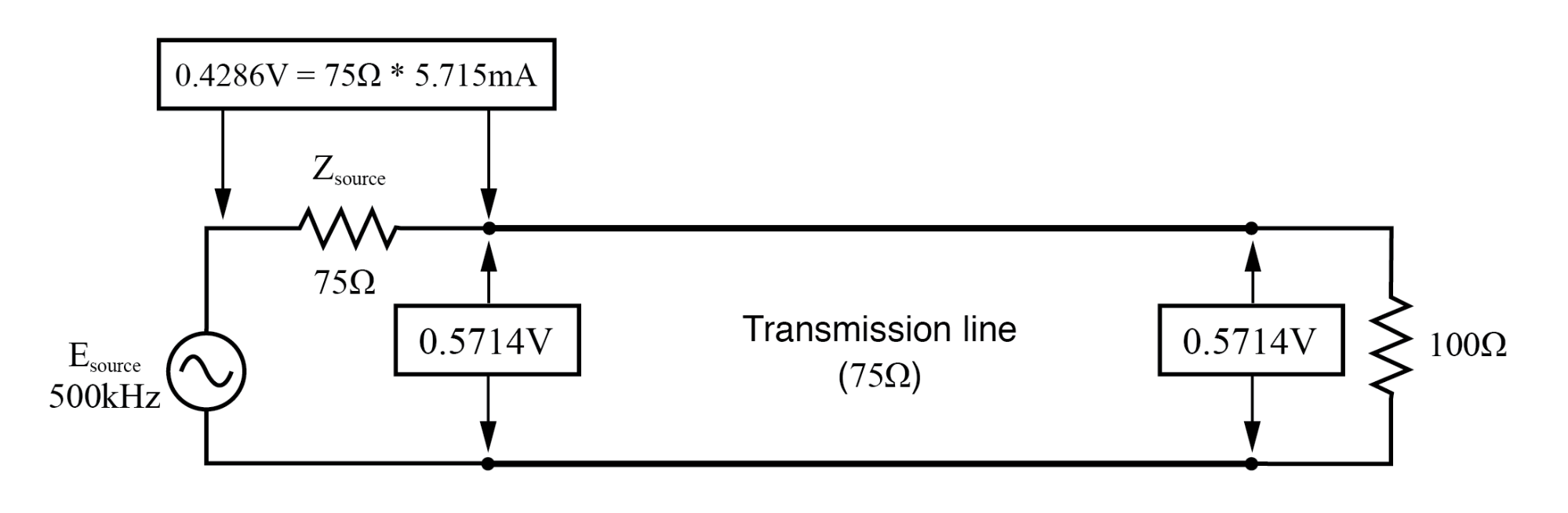
f =500 KHzの場合：入力：V =0.5714、I =5.715 mA;終了：V =5.714、I =5.715mA。

f =750 KHzの場合：入力：V =0.4286、I =7.619 mA;終了：V =0.5714、I =7.619mA。

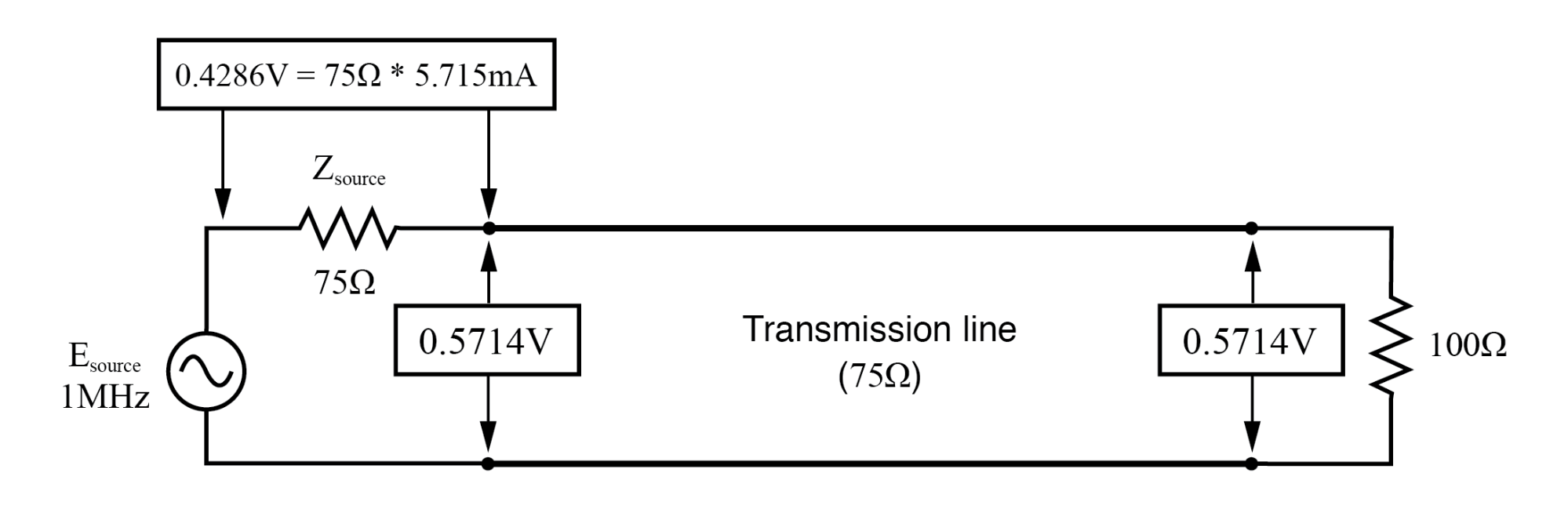
f =1 MHzの場合：入力：V =0.5714、I =5.715 mA;終了：V =0.5714、I =0.5715mA。

基本周波数の奇数次高調波（250 kHz、図3-上記および750 kHz、上記）では、伝送線路の両端で異なるレベルの電圧が見られます。これらの周波数では、定在波がノードの一方の端で終了するためです。もう一方の端は波腹にあります。

開回路および短絡送電線の例とは異なり、この送電線に沿った最大および最小電圧レベルは、0％および100％の電源電圧という同じ極値に達しませんが、「最小」および「最大」電圧。

（図6-上記）同じことが電流にも当てはまります。ラインの終端インピーダンスがラインの特性インピーダンスと一致しない場合、定常電流波のノードに対応する、ライン上の特定の固定位置に最小電流と最大電流のポイントがあります。それぞれ、波腹。

定在波比

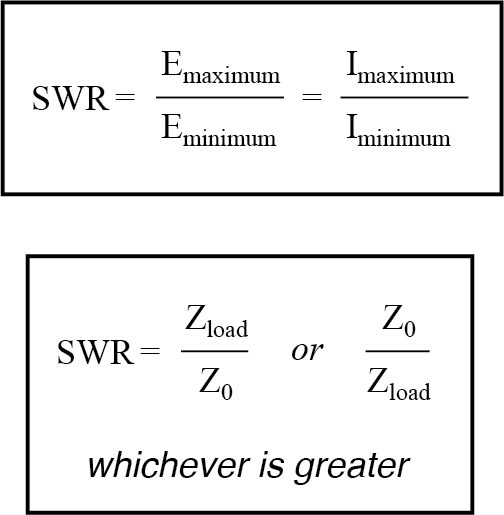
定在波の重大度を表す1つの方法は、電圧または電流の最大振幅（波腹）と最小振幅（節）の比率です。

ラインがオープンまたはショートで終端されている場合、この定在波比 、または SWR 最小振幅はゼロになるため、は無限大で評価されます。有限値をゼロで割ると、商は無限大（実際には「未定義」）になります。

この例では、100Ωのインピーダンスで終端された75Ωのラインで、SWRは有限になります：1.333、250kHzまたは750kHz（0.5714ボルト）のいずれかで最大ライン電圧を取り、最小ライン電圧（0.5714ボルト）で割ることによって計算されます。 0.4286ボルト）。

定在波比は、ラインの終端インピーダンスとラインの特性インピーダンスを取り、2つの値の大きい方を小さい方で割ることによって計算することもできます。この例では、100Ωの終端インピーダンスを75Ωの特性インピーダンスで割ると、正確に1.333の商が得られ、前の計算と非常によく一致します。

完全に終端された送電線のSWRは1です。これは、送電線の長さに沿った任意の場所の電圧が同じであり、電流の場合も同様であるためです。

繰り返しになりますが、これは通常、反射波が負荷に供給されないエネルギーを構成するだけでなく、定常波の波腹によって生成される高い値の電圧と電流が伝送線路の絶縁（高電圧）に過大なストレスを与える可能性があるため、理想的と見なされます。それぞれ導体（高電流）。

また、SWRが高い伝送線路はアンテナとして機能する傾向があり、すべてを負荷に送るのではなく、線路から電磁エネルギーを放射します。放射エネルギーが近くの導体と「結合」して信号干渉を引き起こす可能性があるため、これは通常望ましくありません。

この点に関する興味深い脚注は、アンテナ構造（通常は開放または短絡の伝送線路に似ています）は、多くの場合、高で動作するように設計されていることです。 信号の放射と受信を最大化するという理由から、定在波比。

次の写真（下の図）は、無線送信機システムの接合点にある一連の伝送線路を示しています。両端にセラミック絶縁体キャップが付いた大きな銅管は、50Ωの特性インピーダンスの剛性同軸伝送ラインです。

これらの回線は、無線送信機回路からアンテナ構造の基部にある小さな木製のシェルターにRF電力を運び、そのシェルターから他のアンテナ構造を備えた他のシェルターに運びます。

リジッドラインに接続された柔軟な同軸ケーブル。

リジッドライン（これも50Ωの特性インピーダンス）に接続された柔軟な同軸ケーブルは、シェルター内の容量性および誘導性の「位相」ネットワークにRF電力を伝導します。 2本の剛性ラインをつなぐ白いプラスチックチューブは、一方の密閉ラインからもう一方のシールラインに「充填」ガスを運びます。

ラインはガスで満たされ、内部に水分が溜まらないようになっています。これは、同軸ラインでは明らかに問題になります。フレキシブル同軸ケーブルの導体をリジッドラインの導体に接続するためのジャンパー線として使用される平らな銅の「ストラップ」に注意してください。

なぜ丸線ではなく銅の平らなストラップなのか？表皮効果のため、丸い導体の断面積の大部分が無線周波数で役に立たなくなります。

多くの送電線と同様に、これらは低SWR条件で動作します。ただし、次のセクションで説明するように、伝送線路に定在波が発生する現象は、インピーダンス変換という有用な機能を実行するために利用される可能性があるため、必ずしも望ましくないわけではありません。

レビュー：

• 定在波 は伝播しない（つまり静止している）電圧と電流の波ですが、伝送線路に沿った入射波と反射波の間の干渉の結果です。
• ノード 最小の定在波上のポイントです。 振幅。
• 節 最大の定在波上のポイントです。 振幅。
• 定在波は、終端インピーダンスが伝送線路の特性インピーダンスと一致しない場合にのみ伝送線路に存在できます。完全に終端された回線では、反射波がないため、定在波はまったくありません。
• 特定の周波数では、定在波のノードと波腹が伝送線路の端と相関し、共振が発生します。 。
• 伝送線路の最低周波数の共振点は、伝送線路の長さが1/4波長の場所です。共振点は、基本波（1/4波長）のすべての高調波（整数倍）周波数に存在します。
• 定在波比 、または SWR は、最小定在波振幅に対する最大定在波振幅の比率です。また、終端インピーダンスを特性インピーダンスで除算することによって、またはその逆によって計算することもできます。これにより、最大の商が得られます。定在波のない線（完全に一致：Z _load Z ₀ へ ）SWRが1に等しい。
• 定在波の最大振幅が大きいため、伝送線路が損傷する可能性があります。電圧の腹は導体間の絶縁を破壊する可能性があり、電流の波腹は導体を過熱する可能性があります。