分数微分方程式に基づくスーパーキャパシタエネルギー貯蔵の推定
要約
この論文では、蓄積されたエネルギーの推定にスーパーキャパシタ端子の電圧測定のみを使用した場合の新しい結果を示します。この目的のために、スーパーキャパシタの充電/放電回路の分数次数モデルの適用に基づく研究が行われています。次に、モデルのパラメーター推定値を使用して、スーパーキャパシターに蓄積されたエネルギー量を評価します。得られた結果は、スーパーキャパシタ端子の電圧と電流を測定することによって実験的に決定されたエネルギーと比較されます。すべてのテストは、さまざまな入力信号の形状とパラメータに対して繰り返されます。推定結果と実験結果の間の非常に高い一貫性により、提案されたアプローチの適合性、したがって分数階微積分のスーパーキャパシタエネルギー貯蔵のモデリングへの適用性が完全に確認されます。
背景
今日の時点で、スーパーキャパシタは多くのデバイスやシステムの主要コンポーネントです。たとえば、バックアップ電源や電力回収システム、自動車アプリケーション、ハイブリッド車などです。化学反応を起こさずに電荷を蓄積できるため、このような元素は、一般的なバッテリーと比較して、充電/放電サイクルの数が数百倍になります[1]。さらに、高い充電/放電率により、輸送や再生可能エネルギー源などで使用されるエネルギー回収システムでのアプリケーションに効果的です[2、3]。これらすべてのアプリケーションで重要なパラメータは、スーパーキャパシタに蓄積されたエネルギー量に関する情報です[4、5]。残念ながら、情報を決定できる一般的なコンデンサのよく知られた関係、つまり(1/2) C U 2 、使用できません[6]。蓄積されたエネルギー量は、コンデンサ端子の電圧のみに基づいて決定することはできません。この主な理由は、電荷の再分配に関連する拡散プロセスです[1、7]。これが、多くの研究者が実際のシステムの動作を推定できるスーパーキャパシタモデルを決定しようとしている理由です。現在、研究者は主に RC などの典型的な電子要素の組み合わせを採用しています そのような要素の四極または直列および並列の組み合わせ。ただし、これらのモデルはすべて、スーパーキャパシタの電流とその端子の電圧の関係を、典型的な整数次の微分方程式[3–5、7]の形式で想定しています。
しかし、そのようなシステムにおけるエネルギー推定のいくつかのまったく新しい可能性は、分数階微積分の適用によって得られることがわかります[8、9]。非整数次の微分積分計算は300年以上前に提案されましたが、重要な実装の問題は、コンピューターの出現と離散時間動的システムのモデリングでのコンピューターの使用に関連しています[10–14]。スーパーキャパシタパラメータ推定の問題への分数階微積分の適用は、新しい問題ではありません。この分野には多くの出版物があります[15–25]。著者は、周波数領域と時間領域の両方でパラメータを推定するタスクを実行します[26]。
この論文は、著者の会議のプレゼンテーション[27]の拡張版であり、スーパーキャパシタに蓄積されたエネルギーを推定するために分数次数のアプローチが簡単に紹介されています。
スーパーキャパシタのパラメータを正確に推定することも、それらの信頼性を評価する上で最も重要です[28–31]。スーパーキャパシタ内部の永続的な劣化プロセスにより、等価直列抵抗と静電容量が変化する可能性があります。したがって、提案された方法に基づいてこれらのパラメータを正確に決定することにより、コンデンサの性能を正確に評価することもできます。
このホワイトペーパーは、分数次数の積分と微分に関連するいくつかの予備知識から始まります。次に、試験で使用したパラメータ推定法を示し、分数階微積分に基づく新エネルギー計算法を提案します。結果と考察のセクションでは、さまざまなシナリオで計算されたエネルギーを示し、それらを参照(測定)値と比較します。結論と貢献は結論のセクションに要約されています。
メソッド
スーパーキャパシターでの多孔質材料の使用と電荷蓄積の特定の方法により、整数次微分モデルに基づく従来のアプローチは十分に正確ではありません。多くの研究者が、典型的な RC の組み合わせの形でさまざまなソリューションを提案しています。 定数値または変数値を持つ要素[4、7]。しかし、スーパーキャパシタの電流と電圧の関係を定義するために非整数次の微分計算を使用すると、間違いなくより高い精度が得られることがわかります[17、19]。さらに、このようなソリューションは、非常に高い精度を提供しながら、非常に単純なモデル構造をもたらす可能性があります[18]。
分数次数微分積分学
分数次微分計算は300年以上前から知られています。しかし、物理現象やプロセスのモデリングで人気を博したのは、ここ数年のことです。非整数次の導関数または積分を使用したダイナミクスの記述は、特に新しい材料や技術に基づいて、多くの複雑な現象や工業プロセスの実際の特性をモデル化するための最も効果的な方法の1つであると考えられています[10、12、13 、32–34]。
非整数次微分積分または積分微積分は、αを次数にした古典的な微積分の一般化です。 これは実数のセット\(\ mathcal {R} \)に属します。関数 f の次数\(\ alpha \ in \ mathcal {R} \)の微分積分演算子 ( t )範囲[ a 、 t ]は次のように書くことができます
$$ {{} _ {a} \ mathcal {D} _ {\ textit t} ^ {\ alpha}} f(t)=\ left \ {{\ begin {array} {lcl} {\ frac {\ mathrm {d} ^ {\ alpha} \ textit {f(t)}} {\ mathrm {d} \ textit {t} ^ {\ alpha}}}&\ text {for}&\ alpha> 0 \\ f( t)&\ text {for}&\ alpha =0 \\ \ int_ {a} ^ {t} f(\ tau)\ textrm {d} {\ tau ^ {\ alpha}}&\ textrm {for}& \ alpha <0、\\ \ end {array}} \ right。 $$(1)関数 f を想定 ( t )は複数回微分可能で統合可能です。演算子(1)に関しては、その実現の多くの定義があります。このような定義は、プロパティとアプリケーションの領域が異なります。最も人気のあるのは、リーマン・リウヴィル、カプト、グリュンヴァルト・レトニコフ(GL)の定義です[34]。後者は、このペーパーでは
の形式で使用されます。 $$ {} _ {a} \ mathcal {D} _ {t} ^ {\ alpha} f(t)={\ lim} _ {h \ to 0} \ frac {1} {h ^ {\ alpha} } \ sum \ Limits_ {j =0} ^ {\ left [{\ frac {t} {h}} \ right]}(-1)^ {j} {\ alpha \ choice j} f(t-jh) 、$$(2)ここで、二項\(\ alpha \ choice j \)は次のように定義されます
$$ {\ alpha \ choice j} =\ left \ {\ begin {array} {lll} 1&\ textup {for}&j =0 \\ \ frac {\ alpha(\ alpha-1)\ dots(\ alpha -j + 1)} {j!}&\ text {for}&j> 0。 \ end {array} \ right。 $$(3)離散的な瞬間で分数モデルを取得するために、離散形式のGL定義は
のように簡略化されます。 $$ \ Delta_ {h} ^ {\ alpha} f(t)=\ frac {1} {h ^ {\ alpha}} \ sum \ Limits_ {j =0} ^ {t}(-1)^ {j } {\ alpha \ choice j} f(tj)。 $$(4)GLEqにはいくつかの離散化スキームがあります。 (4)。最も人気のあるものには、後方差分(オイラー)、台形(タスティン)、およびアルアラウイ演算子が含まれます。オイラー法を使用して、離散時間モーメント k での分数導関数
として表示できます $$ \ Delta_ {h} ^ {\ alpha} f(k)=\ frac {1} {h ^ {\ alpha}} \ sum \ Limits_ {j =0} ^ {k}(-1)^ {j } {\ alpha \ choice j} f(kj)、\; k =0,1、\ ldots。 $$(5)以前のサンプルの無限の合計は、限られたメモリと限られた計算時間のために有限値に制限された実際のシステムである必要があります。ここで、GLの切り捨てられたまたは有限長の離散時間近似は
です。 $$ \ Delta ^ {\ alpha} f(k)=\ frac {1} {h ^ {\ alpha}} \ sum \ Limits_ {j =0} ^ {L}(-1)^ {j} {\ alpha \ choice j} f(kj)、\; k =0,1、\ ldots、$$(6)ここで f ( l )=0 for l <0および L はモデルの長さです(6)[23]。サンプル数を減らすと、計算精度が低下します。これは、連続時間で動作するシステムにとって重要です。他の種類のソリューションは、整数次数モデルで分数微分積分を近似するアルゴリズムです。例として、Oustaloup再帰フィルター[35]があります。もう1つの効果的な有限長モデルはFFLDであり、切り捨てられたモデル(6)とLaguerreベースの差異[24、36、37]の組み合わせです。
識別のすべての結果とエネルギー測定は、(長い)観測ウィンドウ L のすべてのサンプルに基づいて取得されます。 、つまり、最大の精度で。図1は、 k について、(6)に基づいて得られた積分と微分のステップ応答を示しています。 =0,1、…、 L 積分/微分次数のさまざまな値α 。次数αの値が異なると仮定する 、さまざまな物理プロセス、特に拡散プロセスをより正確にモデル化できます。
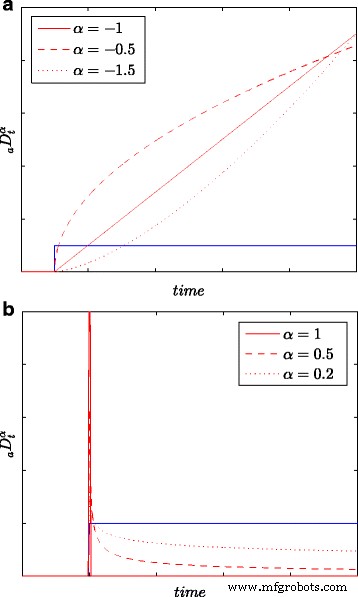
統合するためのステップ応答( a )と差別化( b )さまざまな次数のモデルα
分数モデルのパラメーター推定
このホワイトペーパーに記載されているすべてのエネルギー測定と識別手順の結果は、制御された電圧源から充電されたスーパーキャパシタについて得られたものです。このようなシステムでは、スーパーキャパシタ電流 i C ( t )抵抗器 R で制限する必要があります スーパーキャパシタ C と直列に接続されています (図2)。すべてのスーパーキャパシタパラメータの推定は、4極応答 u に基づいて実行されます。 C ( t )電圧ステップ u ( t )その入力で。微分次数の適切な値の選択α 充電および放電プロセス中の電荷再分配に関連する拡散プロセスに関連する物理現象のスーパーキャパシタモデルを説明することができます。並列抵抗 r P さらに、漏れ電流のモデリングが可能になります。スーパーキャパシタのモデリングに分数微分計算を使用すると、モデル構造の複雑さを軽減できます。電圧源から充電されるスーパーキャパシタの場合、モデルは2つの要素、つまり単純な RC のみで構成されます。 四重極(図2a)。低容量の場合、直列抵抗 r S 重要なのは(図2b)、漏れ電流 I L さらに、並列抵抗 r で表すこともできます。 P (図2c)。分数次の微積分を使用してスーパーキャパシタをモデル化すると、キャパシタ端子の電圧とその電流の関係は次のように表すことができます。
$$ i_ {C}(t)=C _ {\ alpha} \ frac {\ mathrm {d} ^ {\ alpha} u_ {C}(t)} {\ mathrm {d} t ^ {\ alpha}}、 $$(7)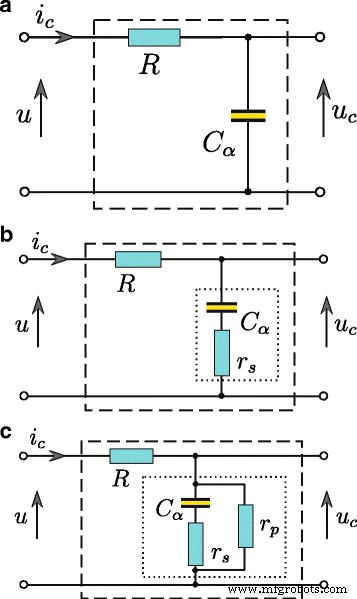
スーパーキャパシタ RC モデル、基本モデル( a )、直列抵抗で拡張( b )、および追加の並列抵抗( c )
ここで、演算子d α / d t α 次数αの微分演算子を意味します および C のSI単位 α は[F /秒 1- α ]。図2aに示されている基本的なスーパーキャパシタの構成は、1次の慣性系として扱うことができ、分数伝達関数で表すことができます。
$$ G(s ^ {\ alpha})=\ frac {U_ {C}(s)} {U(s)} =\ frac {1} {Ts ^ {\ alpha} +1}、$$(8 )。ここで T = R C α 。直列抵抗を考慮に入れる r S (図2b)、回路は伝達関数を備えた位相遅延補正システムとして扱われます([24]と比較)
$$ G(s ^ {\ alpha})=\ frac {1} {T_ {1} s ^ {\ alpha} +1} + \ frac {T_ {2} s ^ {\ alpha}} {T_ {1 } s ^ {\ alpha} +1}、$$(9)ここで T 1 = C α ( R + r S )および T 2 = r S C α 。さらに、並列抵抗 r を考慮に入れます P 漏れ電流を表す I L (図2c)、システム伝達関数は
として表すことができます。 $$ G(s ^ {\ alpha})=\ frac {T_ {2} s ^ {\ alpha} +1} {T_ {1} s ^ {\ alpha} + K}、$$(10)ここで K = R / r P + 1、 T 1 = C ( R r s / r P + R + r S )および T 2 = r S C 。時間領域では、式。 (10)は
として表示できます $$ \ frac {\ mathrm {d} ^ {\ alpha} u_ {C}(t)} {\ mathrm {d} t ^ {\ alpha}} =\ frac {1} {T_ {1}}(u (t)-Ku_ {C}(t))+ \ frac {T_ {2}} {T_ {1}} \ frac {\ mathrm {d} ^ {\ alpha} u(t)} {\ mathrm {d } t ^ {\ alpha}}。 $$(11)(11)で定義されたモデルの時間応答は、それを図3にグラフで示されている形式に変換することによって得られました。ここで、積分および微分演算は分数次数α 。このモデルは、スーパーキャパシタパラメータの推定プロセス中に使用されました。テストされたスーパーキャパシタは、図4aに示されているシステムを使用して識別されました。システム全体の制御手順は、Matlab / SimulinkソフトウェアとxPCToolboxを使用して開発されました。システムは、測定カードNI-DAQがインストールされたデスクトップPC(xPC Target)とマスターコンピューター(xPC Host)で構成されていました。コンピュータはイーサネットネットワークを介して相互接続されました。スーパーコンデンサは、最大±3Aの電流効率の(電圧制御)電圧源(図4b)によって充電および放電されました。測定システムは、100 Hzのサンプリング周波数で動作し、すべての測定およびアナログ制御信号は16ビット分解能で処理[25]。
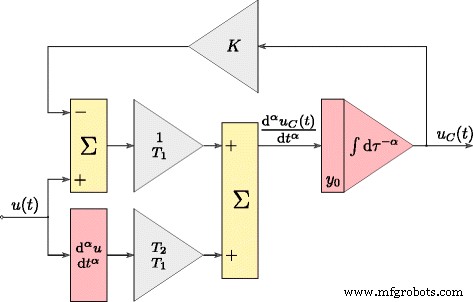
時間領域でのスーパーキャパシタモデルのMatlab構造
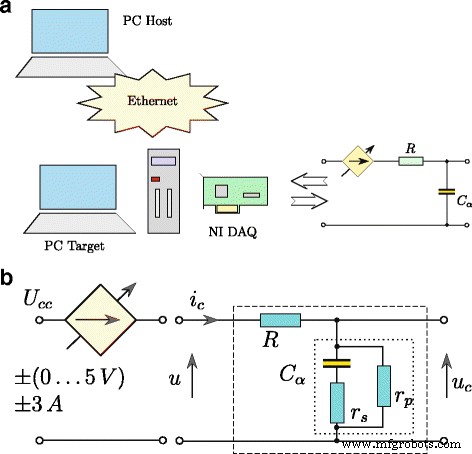
測定システムの構造( a )およびスーパーキャパシタの充電/放電方式( b )
システムの動的特性を決定するための主な方法は、ステップ応答の分析に基づいています[38]。システムモデルに関連して、このメソッドはそのパラメータの推定を可能にします。この研究では、さまざまな電圧(0.5 / 1.0 / 1.5 / 2.0 / 2.7 V)と一定の持続時間(500秒)のステップ信号を使用しました(図5および表2を参照)。一方、スーパーキャパシタの典型的な用途の1つは、電力システムへのエネルギーの蓄積または供給です。この場合、電圧変化率はかなり小さいです。それをシミュレートするために、2Vオフセットの400mVppおよび0.03rad / s信号が使用されました(図6)。さらに、推定パラメータに対する電圧と周波数の変化の影響を調べるために、後者のさまざまな値が使用されました(表3を参照)。
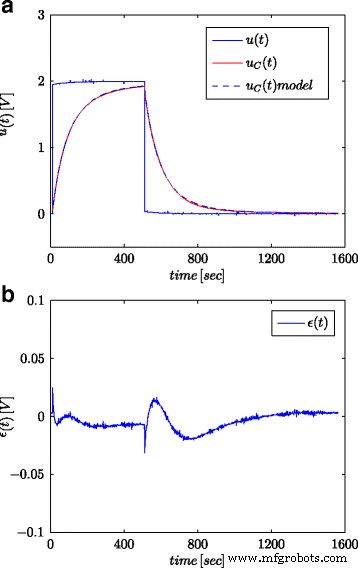
テストされたスーパーキャパシタとそのフラクショナルモデルのステップ応答( a )およびモデル応答エラー( b )
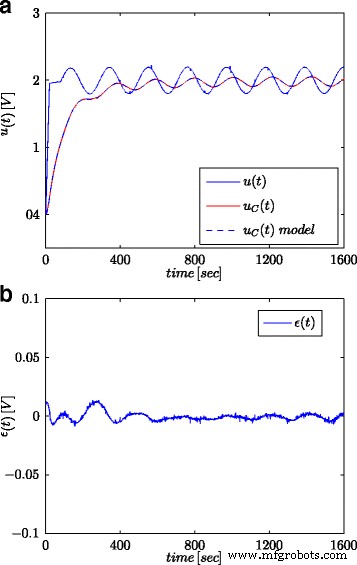
テストされたスーパーキャパシタとそのフラクショナルモデルの正弦波応答( a )およびモデル応答エラー( b )
モデルパラメータの推定にはいくつかの方法があります。この作業で適用される時間領域での識別手順の主な目的は、未知のパラメーターθのベクトルを推定することでした。 =[α 、 C α 、 r S 、 r P ](11)によって提示された分数モデルの。初期誤差を最小限に抑えるために、最小二乗法が使用されました。最適化基準には、標準誤差\(\ | \ epsilon(k)\ | _ {2} ^ {2} \)の最小化が含まれます。ここで
$$ \ epsilon(k)=u_ {C}(k)-\ hat {u} _ {C}(k)、$$(12)ここで u C ( k )は、テストされたシステムから瞬間 k で測定された出力電圧です。 、一方、\(\ hat {u} _ {C}(k)\)は、入力信号 u の対象モデルからの出力電圧です。 ( k )。識別の問題は、パラメータベクトルθを見つけることになりました。 ∈Θ ad それは二乗基準 J を最小化するでしょう
$$ \ min _ {\ theta \ in \ Theta_ {ad}} \ left \ {J =\ sum_ {0} ^ {N} {\ epsilon(k)^ {T} \ epsilon(k)} \ right \} 、$$(13)ここで、Θ ad 許容されるパラメータ値と N のセットを示します シミュレーション時間を意味します。問題を解決するために使用できる多くの最適化アルゴリズムがあります(13)。このホワイトペーパーで紹介する結果は、Matlab環境で遺伝的アルゴリズムを実装することによって得られたものです。
エネルギー計算
スーパーキャパシターに蓄えられるエネルギーの変化は、単位時間あたりにコンデンサーに供給される電力に依存し、次のように説明できます。
$$ \ mathrm {d} E(t)=P(t)\ mathrm {d} t。 $$(14)コンデンサに供給される電力をコンデンサ端子の電流と電圧の積として表すことにより、特定の時間におけるエネルギーの変化 t
として表すことができます $$ \ mathrm {d} E(t)=u_ {C}(t)i_ {C}(t)\ mathrm {d} t。 $$(15)時間間隔中の総エネルギー[ t 1 、 t 2 ]その時間のエネルギー変化を統合することで得られます
$$ E_ {tot} =\ int_ {t_ {1}} ^ {t_ {2}} \ mathrm {d} E(t)=\ int_ {t_ {1}} ^ {t_ {2}} u_ {C }(t)i_ {C}(t)\ mathrm {d} t。 $$(16)式の会計処理。 (7)、総エネルギー貯蔵量は次のように決定できます
$$ E_ {tot} =C _ {\ alpha} \ int_ {t_ {1}} ^ {t_ {2}} u_ {C}(t)\ frac {\ mathrm {d} ^ {\ alpha} u_ {C }(t)} {\ mathrm {d} t ^ {\ alpha}} \ mathrm {d} t。 $$(17)t と仮定します 1 =0および\(E_ {t_ {1}} =0 \)、時間間隔[0、 t の間にスーパーキャパシタに蓄積された総エネルギー ]は
です $$ E(t)=C _ {\ alpha} \ int_ {0} ^ {t} u_ {C}(\ tau)\ frac {\ mathrm {d} ^ {\ alpha} u_ {C}(\ tau) } {\ mathrm {d} \ tau ^ {\ alpha}} \ mathrm {d} \ tau。 $$(18)αの場合は注意してください =1式(18)古典的なものに減らすことができます
$$ E(t)=\ frac {1} {2} Cu_ {C}(t)^ {2}。 $$(19)結果と考察
最初に、分数階微積分を使用してスーパーキャパシタモデルのパラメータベクトルを推定する手順が実行されました。推定は、図2cに示すシステムに基づいて実行され、入力で電圧ステップまたは正弦波が生成されました。モデルの応答は(11)に基づいて計算されました。 2つの識別手順で得られた結果は、特に分数静電容量 C の場合、非常によく似ています。 α そして分数次数α (表1を参照)。直列抵抗の推定値のいくつかの違い r S 周波数への依存の結果である可能性があります。ステップ信号は多くの高周波高調波で構成されていますが、正弦波は1つだけ– 0.03 rad / sです。提示された結果は、定格容量2.7 V、公称静電容量100 F、8m Ωの商用スーパーキャパシタSamwhaGreen-Cap EDLC(DB)で得られたものです。 最大等価直列抵抗( r S )1kHzで。
図5aと6aは、それぞれステップ信号と正弦波信号について測定されたスーパーキャパシタ電圧と計算されたモデル応答を示しています。図5bと6bは、モデルの応答エラーを示しています。
得られたすべての結果は、比較的単純なモデルが提案されたという事実にもかかわらず、モデルの応答と実際の測定値の間の高い一貫性を示しています。いくつかの不一致は、電流源を使用して充電および放電されるスーパーキャパシタのシステムでモデルパラメータを推定する必要があるという事実に起因する可能性があります[25]。また、 r の非常に高い推定値 P この抵抗は、図2cに示すスーパーキャパシタモデルから除外できる可能性があります。これらの非常に高い推定値とさまざまな入力に対する高い不一致は、このパラメーターの推定に使用されるテスト信号が適切でないことを示しています。モデル(10)が最も一般的な形式として使用されました。ただし、すべてのパラメータを正確に決定するには、他の手順とテスト信号を使用する必要がありました。 r の値 P 漏れ電流の特徴 I L 定電圧信号を使用して決定する必要がありますが、非常に長い時間(数十時間程度)です。
この研究の主な目的はエネルギーを測定することでしたが、さまざまな励起条件がすべてのパラメーター推定値に大きく影響しました(表2を参照)。たとえば、スーパーキャパシタ内の拡散現象の影響が大きくなる結果として、電圧ステップ振幅の増加により、分数積分の次数が大幅に変化しました。表2から、スーパーキャパシタは非常に非線形であることがわかります。積分順序の変更の結果として、分数容量の変動も観察されます。これは、正弦波励起にも当てはまります。推定されたパラメータの値-特にα および C α —振幅と周波数によって異なります(表3を参照)。低周波数の場合、振幅値が重要ですが、高周波数の場合、スーパーキャパシタは定電圧で励起されるように動作します。
エネルギー計算
図7aと8aは、図4bに示した構成のスーパーキャパシタの電圧と電流の測定値を示しています。これらの値は、コンデンサに蓄積された総エネルギーの計算に使用されました( E とマークされています)。 1 図1および2 (16)による7bおよび8b)。パラメータ同定プロセスと同様に、計算はシステム入力での電圧ステップと正弦波の両方に対して実行されました。 t ごとにこのように計算されたエネルギー (19)に従って電圧と容量に基づいて計算されたエネルギーと比較されました( E とマークされています) 3 図1および2 7bおよび8b)および分数次微積分で計算されたエネルギー( E としてマーク) 2 図1および2 (18)による7bおよび8b)。式の場合。 (19)、スーパーキャパシタの公称値が採用されました( C n )、(18)では、表1に示されている推定プロセスから得られた値が使用されました。図7bは、電圧ステップの測定結果とエネルギー計算の結果を示しています。図8bは、正弦波の同じ量を示しています。同様の計算が、さまざまな電圧ステップと正弦波励起に対して行われました。図9a、bは、それぞれ0.5Vと2.7Vの2つの電圧ステップで測定および計算されたエネルギーの例を示しています。図10は、周波数が0.03 rad / sec、振幅が0.1 / 0.25 /0.5と0.7Vの正弦波信号のエネルギー変化を示しています。決定されたエネルギー値の違いは、推定値の違いに対応していることがわかります。分数次数のα 。値-1との差が大きいほど、計算されたエネルギーの差が大きくなります。
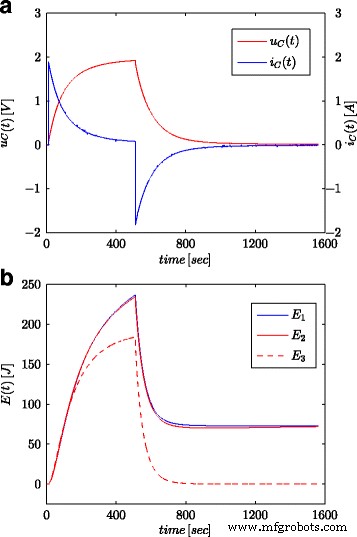
スーパーキャパシタの電圧と電流のステップ応答( a )および計算されたエネルギー値( b )
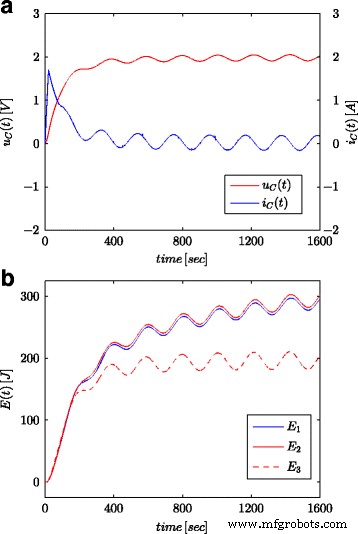
スーパーキャパシタの電圧と電流の正弦波応答( a )および計算されたエネルギー値( b )
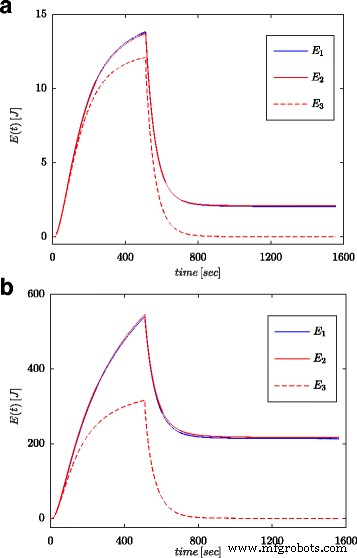
0.5 Vのステップ励起に対して計算されたエネルギー量( a )および2.7 V( b )
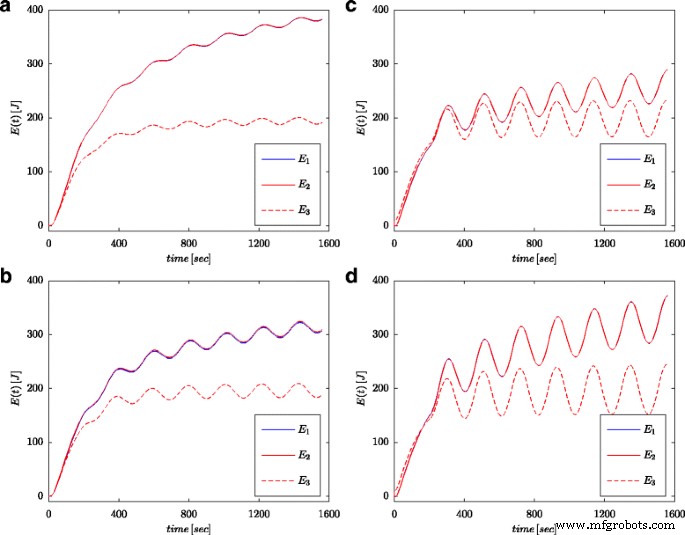
周波数0.03rad / sおよび振幅0.1V( a )の正弦波励起に対して計算されたエネルギー量 )、0.25 V( b )、0.5 V( c )、および0.7 V( d )
ディスカッション
非常に薄いセパレーターによって分離された活性炭の形でスーパーキャパシターに多孔質材料電極を使用し、いわゆる二重層として電荷蓄積メカニズムを使用すると、それらの容量が大幅に増加します。ただし、新しい材料と新しい設計ソリューションを適用すると、整数次の導関数と積分の形式での従来の数学的計算が不正確に見えるという事実が生じます。実施された測定と計算は、スーパーキャパシタの分数次の性質を証明しています。非整数次数の正しい推定によるα 微分/積分の場合、単純な数学的モデルを使用して、スーパーキャパシター内で発生する現象とプロセスを正確にモデル化できます。
(16)によって決定される累積エネルギーの実際の値を考慮すると、公称パラメーター(19)を使用する整数次モデルはエネルギー量を過小評価しますが、分数モデル(18)はほぼ同じ値を示します。
実行されたテストと測定は、電圧源によるスーパーキャパシタの充電と放電に関連していました。産業条件下では、スーパーキャパシタは通常、電流源によって充電および放電されます。コンデンサはもはや慣性システムではなく、典型的な統合システムになるため、これによりシステムの性質が変わる可能性があります。しかし、著者が行った測定は、そのような場合の拡散過程の発生も示しています。とにかく、Gründwald–Letnikov導関数/積分の有用性はここで確認されます。もう1つの問題は、GLの微分積分演算子の実装に関連しています。たとえば、有限または切り捨てられたGLの差(6)は、計算上負担になる可能性があります。今後の調査では、実装の問題を効果的に解決するために、Oustaloup [35]とFFLD [24、36、37]の近似値を比較します。
スーパーキャパシタの端子電圧の測定値のみに基づいてモデル(19)を使用して計算されたスーパーキャパシタのエネルギー貯蔵量は適切ではありません。モデル(19)は、コンデンサ電流がコンデンサ電圧の整数次導関数( i )によって特徴付けられる場合にのみ有効です。 C ( t )=d u C ( t )/ d t )。これは、その構造と使用された特殊な材料の結果として、スーパーキャパシタには当てはまりません。ただし、電流源によって充電される非常に大きなスーパーキャパシタでも同じ問題が発生します。スーパーバッテリーとしては全く新しい要素もあります。これらすべてのアプリケーションで、これらの要素の特定の特性の結果として、電流の変化は端子電圧の整数次導関数によって特徴付けられません。
結論
この論文では、スーパーキャパシタに蓄積されたエネルギー量を推定するための新しいアプローチを提示しました。分析は、分数次数モデルの特定の固有の特性を利用して実施されました。このような高度なモデリングを適用すると、モデル自体がそれほど複雑でなくても、非常に正確な結果が得られることが示されています。これは、スーパーキャパシタでの電荷の再分配と同様に、拡散プロセスをモデル化する非整数次のダイナミクスの自然な能力によるものです。この論文の結果は、スーパーキャパシタの部分的な性質を確認しました。
ナノマテリアル



