コロイド状の高濃度にドープされたZnOナノ結晶の光吸収におけるプラズモン共鳴

背景

ナノ粒子の光学特性の大部分は、励起スペクトルに局在表面プラズモン共鳴（LSPR）が存在することによって決定されます[1–8]。 Kriegel etal。 [2]は、不純物をドープした金属酸化物NC、銅カルコゲニドNC、縮退ドープした半導体NCなど、新たに出現したコロイド状ナノ結晶（NC）の非常に詳細な概要を公開し、それらの光学特性とセンシング、近接場への応用について幅広く議論しました。分光法、調整可能な光電子デバイス、または生物医学的アプリケーションの強化。これらの新しい材料はすべて、過去数十年にわたって広く研究されてきた貴金属NCの代替品です。包括的なレビューについては、参考文献も参照してください。 [9]。さまざまな制御パラメータ[11、13、16–20]に作用することにより、高濃度にドープされた半導体ナノ結晶（NC）の光学応答をIR範囲[10–15]まで調整できることが示されています。ナノフォトニクスの新しい展望。半導体NCの主な利点は、キャリア密度を広い間隔で調整できることです。金属導体の電子密度は固定されていますが、半導体をドープして、10 ¹⁶ の範囲の任意のキャリア密度を実現できます。 ÷10 ²² cm ^-3 [10、13、21、22]。キャリアドーピングにより、THzからIRおよび可視領域までの広い周波数範囲で調整可能なLSPRにアクセスできます[13]。このようなキャリア密度の調整可能性は、半導体ナノ粒子のユニークな特性であり、金属液滴を使用して達成することはできません[23–25]。ドーピングは、結晶格子にさまざまな種類の不純物を組み込むことによって行うことができ[7、10、18]、プラズモン共鳴周波数は、キャリアのアクティブ制御によって調整または切り替えることができます[13、16–18、21、22]。さらに、プラズモン周波数とその線形状は、NCのキャリア密度だけでなく、「バルク状」または「表面状」のドーピングの種類にも依存します[15、22]。前者の場合、自由キャリアの電荷は、NCボリューム全体に不純物をドープする電荷によって中和されますが、後者の場合、自由キャリアは、NCボリュームにある周囲の媒体からドナー/アクセプターによってNCボリュームに注入されます。 NCインターフェース。

半導体ナノ粒子の光学応答の理論的研究により、量子力学的記述と古典的記述の間に有意差があることが明らかになりました[5、22、24、26]。ナノ粒子のサイズが小さくなると、プラズモン共鳴はより高いエネルギーにシフトし、古典的な予測からの目に見える偏差が生じます[5、21、22]。さらに、高濃度にドープされたNCの動的特性は、サイズ量子化レジームからプラズモン振動の古典的なレジームに移行します[22]。キャリア数またはNCサイズを変えることで観察できます。

この作業では、参考文献で実験的に調査されたような光ドープZnONCの光学応答の理論的分析を提示します。 [21、27]。これらの実験的研究では、固定サイズとキャリア密度のコロイド状ZnONCの光吸収断面積が測定されました。伝導帯の光電子は、フォトドーピングプロセスによってZnO NCで生成され、一方、正孔は周囲のトルエンの正孔捕捉中心によってトラップされました。平均伝導電子濃度 n _e 異なる半径（1.75〜6 nm）のほぼ球状の光ドープナノ結晶では、上限（1.4±0.4）×10 ²⁰ に達することがわかりました。 cm ^-3 [21、27]。バンド内吸光度は0.2〜1.0 eVの範囲で測定され、古典的なドルーデモデルの予測との有意差が観察されました。著者らは、単一粒子遷移に基づく量子力学的アプローチが、定性的にのみ共鳴周波数の実験的なサイズ依存性をもたらすことを示しました[21]。

この記事の目的は、相互作用しない単一粒子近似を超えて、光ドープZnO NCにおけるプラズモン共鳴の理論的アプローチを再検討することです[21、27]。これは、局所交換を伴うランダム位相近似（RPA）内での伝導電子の自己無撞着な多体量子力学的処理に基づいています[28]。半導体ナノ粒子の自由電荷キャリアが原子のようなシェルを形成することが示されました[29、30]。局所密度近似（LDA）コーン・シャム方程式を解いて、電子殻構造を記述します。集団プラズモン励起の原因となる電子相関は、RPA内で考慮されます。 ZnO NCのプラズモン共鳴は、金属液滴のよく知られている三重共鳴とは大幅に異なることを示します。バルク状にドープされたNCとは異なり、表面状にドープされたZnONCには正電荷の回復はありません。その結果、自由電子間のクーロン反発により、自由電子はNC表面に近づきます。次に、この特定の電子配置は双極子モードにつながります。このモードでは、角度の自由度のみが励起され、電子的な半径方向の動きは含まれません。電子が純粋な並進振動を受ける通常の三重表面双極子プラズモンとは対照的に、高度にドープされたZnO NCの電子は、フラーレン分子のプラズモン振動と同様に、かなり薄い電子殻内で接線方向の振動を受けます[31]。また、このプラズモンモードの古典的から量子閉じ込め領域への遷移は、NCサイズと有効ボーア半径の比によって支配され、自由電子の数に依存しないことも示しています。プラズモン振動の量子効果は、実験的に観察されたLSPRサイズ依存性とよく一致する双極子共鳴周波数の青方偏移をもたらします[21]。

メソッド

研究の目的は、光ドープされたZnOナノ結晶の光学特性の理論的分析です。粒子数が変化するシステムの基底状態構成は、局所密度近似内で計算されました。基底状態の波動関数は、コーン・シャム方程式のセットの自己無撞着な数値解法によって得られた単一粒子エネルギーです[32]。単一粒子状態の完全な基底は、Bスプライン法[33]を使用して、有限数のBスプラインにわたって大きな半径の空洞内の基底関数を拡張することによって生成されました。キャビティ半径はNC半径と等しくなるように選択されました。 Bスプライン離散基底を使用した計算の望ましい精度は、計算で使用されるBスプラインの数と順序を適切に選択することによって達成されました。十分な精度（10 ^-5 ）を達成するために、7次の50個のBスプラインを使用しました。 ）結果の。固有システムサブルーチンパッケージ（EISPACK）の標準サブルーチンRGは、RP​​A行列方程式[28]の固有値と固有ベクトルの取得に使用されています。このソリューションは、双極子励起エネルギーと対応する振動子強度のセットを提供します。光吸収スペクトルは、固定された折り畳み幅のローレンツプロファイルによって計算された振動強度分布を広げることによって得られました。

結果と考察

基底状態の構造

N のシステムを検討します 半径 R のZnONC内に局在する伝導帯電子 。 [21]に続いて、電子の数はNCサイズによって N と変化すると仮定します。 =4 π n _e R ³ / 3、ここで固定平均電子濃度、 n _e =1.4×10 ²⁰ cm ^-3 は、フォトドーピングプロセスで達成可能な最高レベルによって決定されます。考慮されるNCの半径は2.4〜6nmの範囲です。したがって、伝導電子の数、 N 、8から128まで変化します。

R と仮定して、エンベロープ関数近似を使用して電子の運動を記述します。 格子定数よりはるかに大きいです。バルクZnOの電子バンド構造は、非等方性および非放物線状のエネルギースペクトルによって特徴付けられることが知られています[34]。ただし、 N の集合ダイナミクスの現在の問題については 非局在化電子の場合、これらの小さなエネルギースペクトル効果を無視し、有効質量\（m_ {e} ^ {*} =0.3〜m_ {e} \）の等方性放物線エネルギー分散を検討します[34]。同じ理由で、ZnONCは球形システムと見なされます。

NC界面での高い伝導バンドオフセットにより、電子はZnO NCボリューム内に強く局在化するため[6]、NC境界ですべての電子波動関数が消滅するように強制します r = R 。したがって、 N を検討します 相互作用する電子は、NC内に電界を生成しない正の電荷表面分布によって全体的な電荷の中性が保証される、無限の球形のウェル内に局在します。検討対象のシステムの有効なハミルトニアンは次のとおりです。

ここで、 V （ r _a 、 r _b ）は、対電子クーロン相互作用を表します。 ZnO材料と周囲の媒体の分極を説明するその明示的な表現は、多重極展開として記述されます[3]、

ここで r _< および r _> それぞれ、2つの半径方向の位置の最小値と最大値です。 ZnOとトルエンの誘電率にはバルク値εが割り当てられます _i =3.7およびε _m それぞれ=2.25 [21]。これらのパラメータを使用すると、有効ボーア半径\（a_ {0} =\ hbar ^ {2} \ varepsilon _ {i} / m_ {e} ^ {*} e ^ {2} =0.65 \）nmはNC半径。

単一粒子の電子エネルギー、ε _i 、および包絡線波動関数ψ _i LDAコーン-シャム方程式のセットを満たす

ここで、平均場ポテンシャル V _mf 直接の V の合計で与えられます _D （ r ）、交換、 V _x （ r ）、パーツ、

\（\ rho =\ sum _ {i} | \ psi _ {i} | ^ {2} \）は電子密度です。 Dirac形式の局所密度依存交換項を、通常行われているより現実的な局所密度依存交換相関項に置き換えることができることに注意してください。それに続く励起状態の理論的構築がRPAの性質の基底状態相関の大部分を自動的に説明するため、これは行いません。

簡単にするために、閉じた電子殻を持つ球対称の電子配置を検討します。この場合、単一粒子の波動関数は、放射状、角度、およびスピン成分の積として与えられます[35]。したがって、インデックス i =（ n 、 l ）、ここで n は放射状量子数であり、 l 角運動量1。式の数値解法。 （3）電子数 N の場合 <130は、基底状態の電子配置が、半径方向の量子数が最も低い占有電子状態で構成されていることを示しています n =1。これらの電子状態にはノードのない放射状波動関数があり、角運動量 l の値が異なります。 。したがって、スピン縮退を考慮すると、このような対称構成の「魔法」の電子数は N です。 =2（ l _max +1） ² 、ここで l _max は、最も高い占有電子状態の最大角運動量です。図1に、密度分布ρを示します。 （ r ） N のNCの場合 =18、50、128電子。サイズが大きくなるにつれて、半径方向の密度分布がますます狭くなり、NCインターフェースに向かってシフトすることがわかります。図1の挿入図は、電子動径分布の平均電子値のサイズ依存性を示しています〈 r 〉 NC半径 R と比率δ r / R 、その分散の\（\ delta r =\ sqrt {\ langle r ^ {2} \ rangle-{\ langle r \ rangle} ^ {2}} \）（これは有効な電子殻幅と見なすことができます） NC半径。この比率は、 N の最小のNCでは約0.15にすぎません。 =8電子は、より大きなシステムでは急速に減少します。数値的には、電子殻の幅δ r 有効ボーア半径の約3分の2です a ₀ 一方、電子殻のピークは、量子反射により約 R だけNCインターフェースからシフトします。 − 〈 r 〉≃2 a ₀ 。電子システムのこの特徴は、電子をNC境界に押し出し、中空の球形電荷分布を形成する強力なクーロン反発に由来します。 NC半径が十分に大きい場合、NC境界でのクーロン反発力 e ² N / ε _i R ² 遠心力よりもはるかに強くなります\（\ hbar ^ {2} l（l + 1）/ m_ {e} ^ {*} {\ langle r \ rangle} ^ {3} \） \（l =l_ {max} =\ sqrt {N / 2} -1 \）。それらの比率が a であることがわかります ₀ / 2 R 。 R の場合、半径方向と角度方向の電子運動が分離するのはそのためです。 ≫ a ₀ 。この場合、電子システムは量子回転子に似ています。たとえば、占有された単一粒子状態のエネルギースペクトルε _i 式の（3）は次の式でよく近似されます。

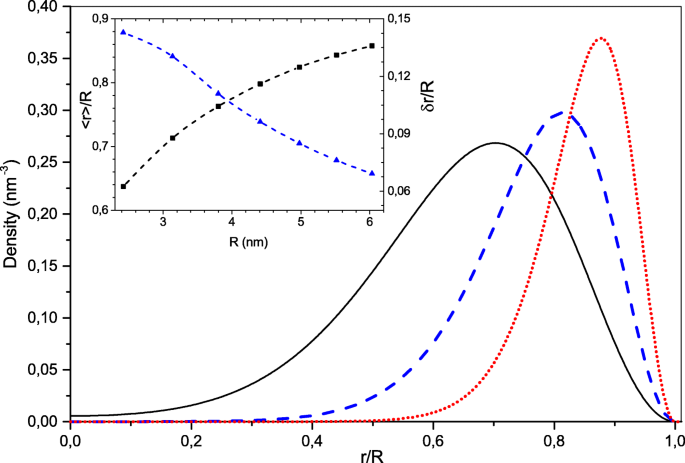
非局在化電子の数が異なるNCの放射状密度分布 N =18（黒の実線のような）、50（青い破線）、128（赤い点線）。挿入図では、縮小された平均半径（黒）とその分散（青）がNC半径の関数として表されています

光学応答

線形応答近似では、外部高調波電界が同じ周波数の時間依存の自己無撞着電界を誘導します。対応する小振幅振動の知識は、双極子励起状態、および基底状態と励起状態の間の遷移確率に関する情報を提供します。基底状態がスレイター行列式であるシステムの場合| Φ ₀ >、RPAアプローチ内の相関多体双極子励起状態は、粒子-正孔励起の線形重ね合わせとして構築されます[36]：

。 $$（6）

インデックス i 、 m 、（ j 、 n ）フェルミ準位Fの上（下）の単一粒子状態を参照してください。 \（\ hat {a} ^ {+} \）と\（\ hat {a} \）は、それぞれ作成と破棄の単一粒子演算子です。

順方向の振幅\（X_ {ij} ^ {\ nu} \）と逆方向の振幅\（Y_ {ij} ^ {\ nu} \）は、行列RPA方程式を解くことによって取得できます[ 28]：

$$ \ left（\ begin {array} {ll} \ mathbf {A}＆\ mathbf {B} \\ \ mathbf {B} ^ {\ star}＆\ mathbf {A} ^ {\ star} \ end { array} \ right）\ left（\ begin {array} {l} \ mathbf {X} ^ {\ nu} \\ \ mathbf {Y} ^ {\ nu} \ end {array} \ right）=\ omega_ { \ nu} \ left（\ begin {array} {l} \ mathbf {X} ^ {\ nu} \\-\ mathbf {Y} ^ {\ nu} \ end {array} \ right）、$$（7 ）。

ここで、固有値ω _ν 励起エネルギーです。行列 A および B 次のように定義されます

$$ {\ begin {aligned} A_ {ij、mn}＆\、=\、\ delta_ {im} \ delta_ {jn} \ left（\ varepsilon_ {i}-\ varepsilon_ {j} \ right）\、+ \、\ left \ langle in \ left | \ hat {v} \ right | jm \ right \ rangle、\ quad B_ {ij、mn}＆\、=\、\ left \ langle im \ left | \ hat {v} \ right | jn \ right \ rangle \\ \ hat {v}（\ mathbf {r}、\ mathbf {r} ^ {\ prime}）＆=V（\ mathbf {r}、\ mathbf {r} ^ {\ prime} ）+ \ delta \ left（\ mathbf {r}-\ mathbf {r} ^ {\ prime} \ right）\ delta V_ {x} / \ delta \ rho。 \ end {aligned}} $$（8）

逆方向の振幅\（Y_ {ij} ^ {\ nu} \）は、電子正孔基底状態相関の寄与を測定することに注意してください\（\ hat {a} _ {j} ^ {+} \ hat { a} _ {i} | \ Phi _ {0}> \）、それぞれ、励起状態の励起| Φ _ν >周波数ω _ν 。

対応する双極子振動子強度 f _ν RPA振幅 X で表されます ^ν および Y ^ν 、

$$ f _ {\ nu} =\ frac {2 m_ {e} ^ {*} D ^ {2} _ {\ nu} \ omega _ {\ nu}} {\ hbar ^ {2}}、\ quad D_ { \ nu} =\ sum_ {ij} \ left（X ^ {（\ nu）} _ {ij} d_ {ij} + Y ^ {（\ nu）} _ {ij} d_ {ji} \ right）、$ $（9）

ここで d _ij =〈 i | z | j 〉は単一粒子の双極子行列要素です。

光吸収断面積は、0.2 ωの折り畳み幅でローレンツプロファイルによって計算された振動子強度分布を広げることによって得られました。 。 N のNCの振動子強度分布と一緒の光吸収スペクトル =8（a）、32（b）、50（c）、および128（d）の電子を図2に示します。図2dでは、計算された光吸収断面積を参考文献の実験データと比較します。 [21] R を使用したZnONCの場合 ≃6nm。考慮されるすべてのNCで、スペクトルは単一の共鳴線によって支配され、その位置が実際に光吸収断面積の最大値を決定することがわかります。確かに、単一粒子の電子スペクトルは量子回転子に似ているので、それは予想されます。最も強い遷移は、最大波動関数がオーバーラップしている場合、つまり、半径方向の量子数が等しい場合に発生します n 。私たちの場合、最も高い占有状態 j からのそのような光学遷移は1つだけです。 =（1、 l _max ）最も低い空の状態に i =（1、 l _max +1）。ただし、対応する双極子励起は、強いクーロン反発によって電子相関が重要で圧倒的になる場合は常に、相互作用しない単一粒子遷移とは大きく異なります。これは、 R の場合です。 ≫ a ₀ 。つまり、集団励起のエネルギーω _ν 、単一粒子遷移のエネルギーを超えています

$$ \ Delta =\ left（\ epsilon_ {1、l_ {max} +1}-\ epsilon_ {1、l_ {max}} \ right）=\ frac {\ hbar ^ {2}（l_ {max} + 1）} {m_ {e} ^ {*} {\ langle r \ rangle} ^ {2}}。 $$（10）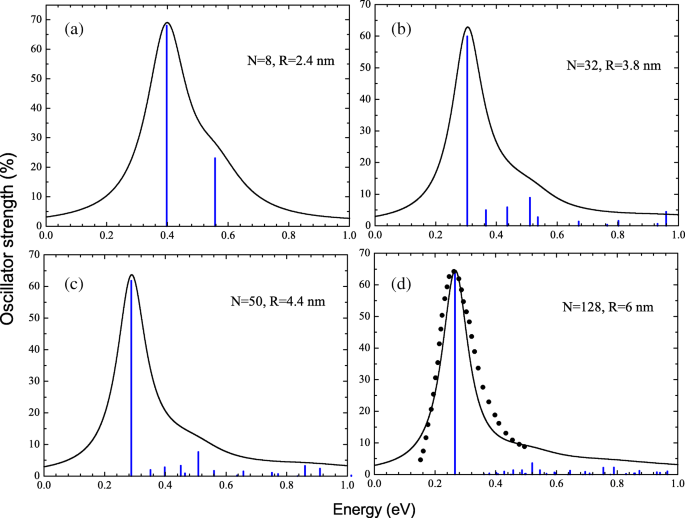

N のNCのRPAEアプローチ内で計算された振動子強度分布と対応する光吸収ピークプロファイル =8（ a ）、32（ b ）、50（ c ）、および128（ d ）伝導帯電子。 R を使用したNCの実験[21]（黒い四角）と計算された（実線）共鳴ピークプロファイルの比較 ≈6nm（ d ）

図3では、光吸収極大ωの位置を比較しています。 _res 、ここで計算（青い円）、[21]（赤い星）の実験結果。実験データと私たちの理論結果の間に顕著な一致が見られます。比較のために、ここではエネルギーΔもプロットします。 単一粒子遷移の（緑色の四角）。電子相関は、Δと比較して集団励起エネルギーを大幅に増加させます 。 RPA方程式の簡単な分析。 （7）はこの観察を説明しています。 j からの主な光学遷移のみを考慮する場合 =（1、 l _max ）から j =（1、 l _max +1）状態、RPAEq。 （7）は2×2の行列方程式になり、固有値ω 単純です：

$$ \ omega ^ {2} =\ Delta ^ {2} + 2V \ Delta、$$（11）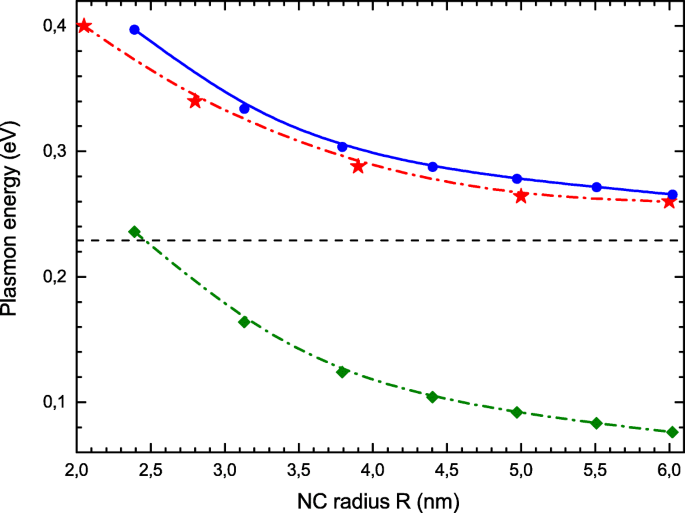

LSPRエネルギーのサイズ依存性。実験値[21]（赤い星）、局所交換を伴うRPA（青い円）、単一粒子遷移のエネルギー（下の曲線の緑のひし形）。古典的な値（13）は、水平の破線で示されています

ここで、\（V =\ left \ langle ij \ left | \ hat {v} \ right | ij \ right \ rangle \）は、RPAクーロン行列要素を示します。 r.h.sの最初の用語式の（11）は単一粒子の寄与を示しますが、第2項は粒子と正孔の相互作用から生じます。それらの比率は、表面の電子の半径座標 r をとることによって推定できます。 = R RPAマトリックス要素 V 、および交換期間を無視します。この見積もりにより、

が得られます。 $$ \ frac {2V} {\ Delta} \ simeq \ frac {4R \ varepsilon_ {i}} {a_ {0}（\ varepsilon_ {i} +2 \ varepsilon_ {m}）} \ simeq \ frac {2R} {a_ {0}}。 $$（12）

したがって、 R の場合、電子相関の寄与が支配的です。 ≫ a ₀ 。大きなNCの限界では、電子密度分布はNC表面に集中します。したがって、式によると。 （12）、式の共鳴エネルギー。 （11）傾向があります

$$ \ omega =\ sqrt {\ frac {2 \ hbar ^ {2} e ^ {2} N} {m_ {e} ^ {*}（\ varepsilon_ {i} +2 \ varepsilon_ {m}）R ^ {3}}}、$$（13）

これは、薄い球殻の古典的な双極子プラズモン周波数と正確に一致します[37]。このプラズモンモードは、接線方向の電子振動に対応します。このように、 C の表面プラズモン共鳴に似ています。 ₆₀ 分子。ここで、共振周波数は式（1）に類似した方程式でよく表されます。 （13）[38]。フラーレンの場合[39]と同様に、このプラズモンモードは総振動強度の3分の2を収集することに注意してください（図2を参照）。これは、この振動が角度の自由度のみを含み、半径方向の動きを乱さないようにするために発生します。

純粋に並進である均質な球におけるよく知られている双極子表面プラズモンモードとは対照的に、現在の考慮のモードは圧縮である。誘導された密度は、このプラズモンモードの復元力の役割を果たす表面に平行な電界を生成します。さらに、誘導された密度振動による局所フェルミ準位の純粋な量子変動が復元力に寄与します。共振周波数への対応する量子圧力の寄与は、Δによって与えられます。 式の項（11）。有効ボーア半径 a が小さいため、考慮されるすべてのNCでのクーロン寄与よりも小さくなります。 ₀ ZnOで。ただし、 a の値が大きいNCでは ₀ 、 R で古典的な双極子プラズモン共鳴から量子閉じ込め領域への遷移を観察できます。 〜 a ₀ 。ドープされたNCの場合、パラメータ a は注目に値します。 ₀ / R 双極子共鳴の古典的/量子的性質を制御するものは、NCサイズのみに依存し、自由キャリアの数には依存しません N 。

図3で、水平線は古典的なプラズモン共鳴エネルギーを示しています（13）。その古典的な値に対する共鳴周波数の青方偏移は、2つの量子効果、上記の量子圧力の寄与と平均電子半径の減少によって引き起こされます。後者は、< r のように、境界からの量子反射によって電子がNCボリュームに押し込まれるために発生します。 〉≃ R −2 a ₀ 。この効果により、マトリックス要素 V が増加します。 これにより、共振周波数が増加します。大まかに言って、この効果はNC半径 R を置き換えることで再現できます。 式の分母で。 （13）〈 r 〉。式によると。 （11）–（13）、両方の効果は、逆NC半径∝1 / R に比例する青の周波数シフトを提供します 。ただし、数値的には、最後のものの寄与が最大です。

結論

この手紙を締めくくるために、我々は、高度にnドープされたコロイド状ZnONCで観察される強い双極子共鳴をうまく予測する理論を考案しました。新しいタイプの表面双極子プラズモン励起は、多体量子アプローチを使用して理論的に研究されています。我々は、光ドープされたZnOナノ結晶の強いクーロン反発が、内面に近い薄い表面層に局在する特定の基底状態の電子分布をもたらすことを実証しました。双極子が励起されると、この電子分布は、本質的に角運動で形成される集団プラズモン振動を維持します。この表面プラズモンモードの古典的から量子閉じ込めレジームへの移行は、ナノ結晶サイズと有効ボーア半径の比に等しい単一のパラメーターによって支配されます。 NCインターフェースからの電子反射により、電子殻の半径が小さくなります。その上、局所的なフェルミ準位の変化は、プラズモン発振器の復元力に追加の貢献をします。これらの量子効果は、共鳴プラズモン周波数のサイズ依存性につながります。これは、実験的観測との顕著な一致です。大きなNC半径の限界では、共鳴線は、微小幅の帯電したシェルの古典的なプラズモン周波数にスムーズに向かう傾向があります。

略語

LDA：

局所密度近似

LSPR：

局在表面プラズモン共鳴

NC：

ナノクリスタル

RPA：

ランダム位相近似