連立方程式の解法：代入法と加算法

この一連の方程式には、 x の値の組み合わせは1つだけです。 および y それは両方を満たすでしょう。

どちらの方程式も、個別に検討すると、有効な（x、y）の無限大があります。 ソリューションですが、一緒に 1つだけです。グラフにプロットすると、この状態が明らかになります：

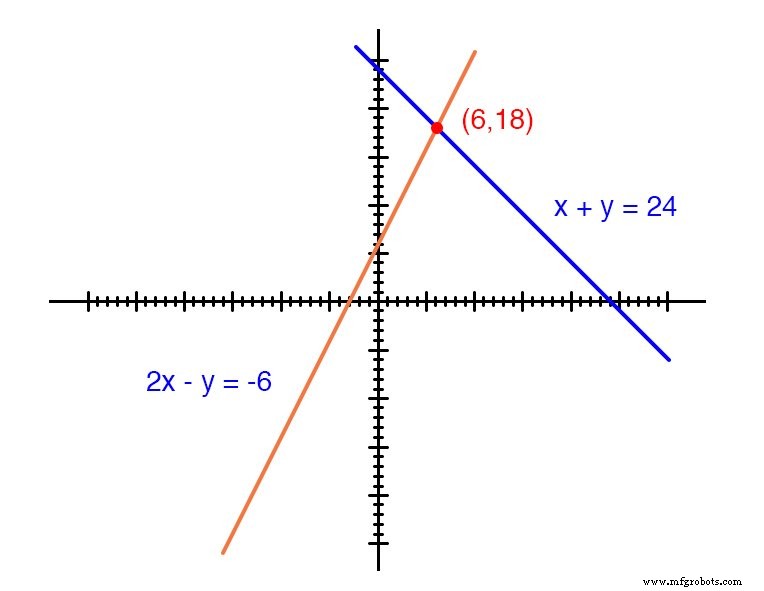
各線は、実際には可能な x を表す点の連続体です。 および y 各方程式の解のペア。

各方程式には、個別に、無限の数の順序対（ x ）があります。 、 y ）ソリューション。 2つの線形関数 x + y =24 が存在するポイントは1つだけです。 および 2x --y =-6 交差し（多くの独立した解の1つが両方の方程式で機能する場合）、ここで x は6の値に等しく、 y 18の値に等しい。

ただし、通常、グラフ化は、2つ以上の方程式の連立解集合を決定するための非常に効率的な方法ではありません。 3つ以上の変数のシステムでは特に実用的ではありません。

たとえば、3変数システムでは、解は3次元座標空間内の3つの平面の点の交点によって見つけられますが、視覚化するのは簡単なシナリオではありません。

置換法を使用した連立方程式の解法

連立方程式を解くための代数的手法がいくつか存在します。

おそらく最も理解しやすいのは置換です メソッド。

たとえば、2変数の問題の例を考えてみましょう。

置換方法では、一方の変数がもう一方の変数に関して定義されるように、方程式の1つを操作します。

次に、この新しい定義 1つの変数と substitute 他の方程式の同じ変数に対してそれを行います。

この場合、 y の定義を採用します。 、これは 24-x これを y の代わりに使用します 他の方程式で見つかった項：

これで、変数が1つだけの方程式ができました（ x ）、「通常の」代数手法を使用してそれを解決できます：

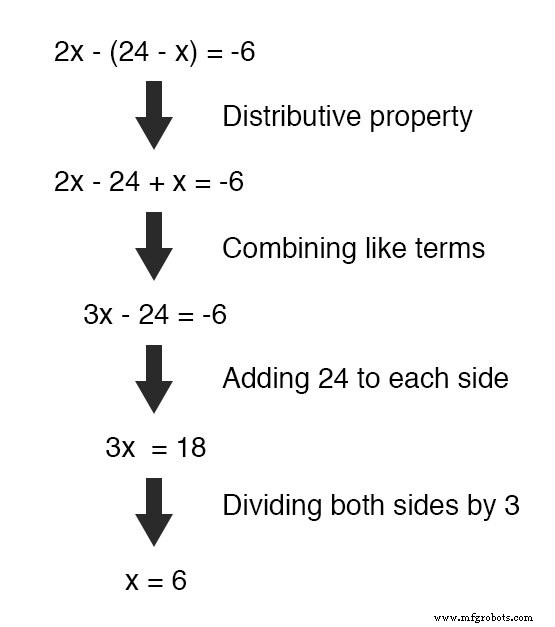
これで x がわかっている場合は、この値を元の方程式のいずれかに接続して、yの値を取得できます。

または、作業を節約するために、この値（6）を生成した方程式に代入して y を定義することもできます。 x の観点から 、それはすでに y を解くための形になっているということです ：

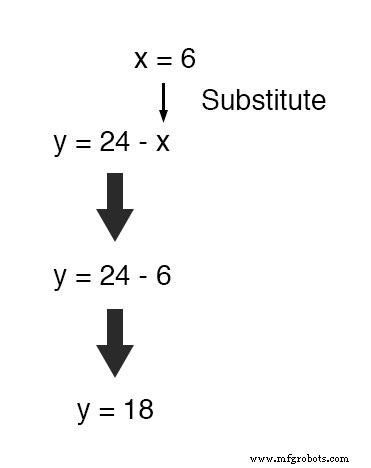
3つ以上の変数のシステムに置換方法を適用するには、同様のパターンが必要ですが、より多くの作業が必要になります。

これは一般に、どのような解決方法にも当てはまります。解決策を取得するために必要なステップ数は、システムに変数を追加するたびに急速に増加します。

3つの未知の変数を解くには、少なくとも3つの方程式が必要です。この例を考えてみましょう：

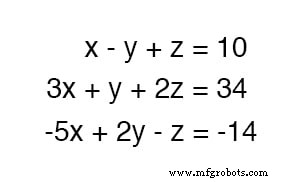
最初の方程式は最も単純な係数（ x の場合は1、-1、および1）を持っているため 、 y 、および z 、それぞれ）、他の2つの観点から1つの変数の定義を作成するためにそれを使用することは論理的であるように思われます。

x を解く y の観点から および z ：

これで、この x の定義に置き換えることができます。 ここで、 x 他の2つの方程式に現れます：

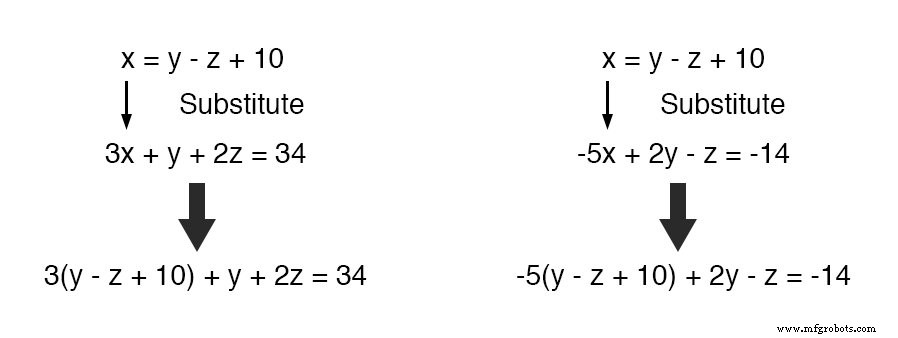
これらの2つの方程式を最も単純な形式に変換します。

これまでのところ、私たちの努力により、システムは3つの方程式の3つの変数から2つの方程式の2つの変数に削減されました。

これで、2つの方程式 4y --z =4 に置換手法を再度適用できます。 および -3y + 4z =36 y のいずれかを解決する または z 。まず、最初の方程式を操作して z を定義します y の観点から ：

次に、この z の定義に置き換えます y の観点から z が表示される場所 他の方程式では：

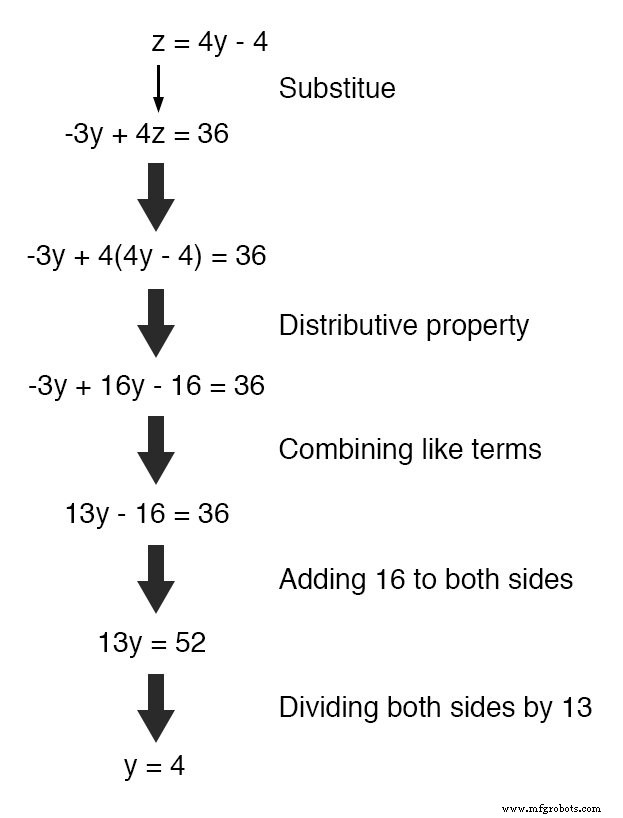
これで y は既知の値であるため、 z を定義する方程式にプラグインできます。 y の観点から z の数値を取得します ：

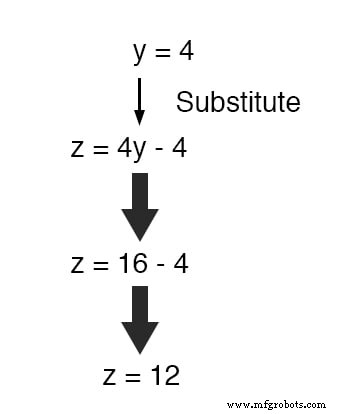
ここで、 y の値を使用します および z 既知のことですが、これらを x を定義した方程式に組み込むことができます。 y の観点から および z 、 x の値を取得します ：

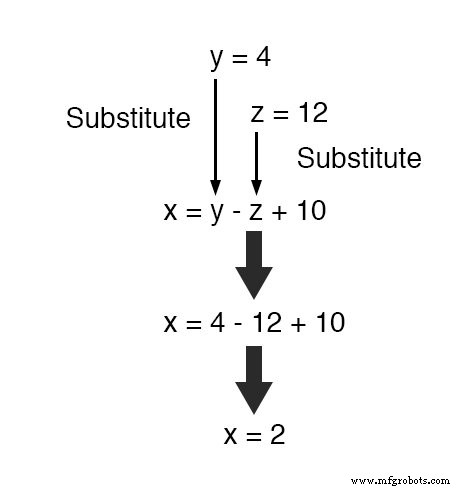
最後に、 x の値を見つけました 、 y 、および z 3つの方程式すべてを満たす2、4、および12のそれぞれ。

加算法を使用した連立方程式の解法

代替方法は概念レベルで理解するのが最も簡単かもしれませんが、私たちが利用できる解決策は他にもあります。

そのような方法の1つは、いわゆる加算です。 変数の項をキャンセルする目的で方程式を相互に追加する方法。

置換方法を示すために使用される2変数システムを見てみましょう：

代数の最もよく使われる規則の1つは、方程式に対して両側に等しく実行する限り、任意の算術演算を実行できるというものです。 。

加算に関しては、これは、方程式の両辺に、同じである限り、任意の量を加算できることを意味します。 量—方程式の真理を変えることなく。

したがって、私たちが持っているオプションは、方程式の対応する辺を足し合わせて新しい方程式を形成することです。

各方程式は等式の表現であるため（ =の両側で同じ量） 記号）、一方の方程式の左側をもう一方の方程式の左側に追加することは、2つの方程式の右側も一緒に追加する限り有効です。

たとえば、方程式セットの例では、 x + y を追加できます。 to 2x --y 、および 24 を追加します および -6 一緒に新しい方程式を形成します。

これは私たちにとってどのようなメリットがありますか？方程式セットの例に対してこれを行うとどうなるかを調べます。

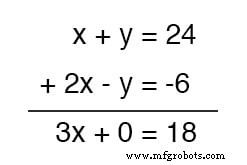
上の方程式にはたまたま正の y が含まれているためです。 下の方程式に負の y が含まれている間 用語、これら2つの用語は追加の過程で互いにキャンセルされ、 y は残りません。 合計の項。

残っているのは新しい方程式ですが、未知の変数 x が1つしかない方程式です。 ！これにより、 x の値を簡単に解くことができます。 ：

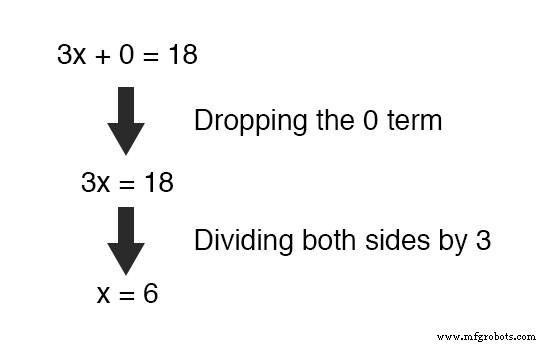
x の既知の値が得られたら もちろん、 y を決定します の値は単に置換の問題です（ x を置き換える） 番号は 6 ）元の方程式の1つに。

この例では、方程式を足し合わせる手法がうまく機能して、単一の未知の変数を持つ方程式を生成しました。

物事がそれほど単純ではない例はどうですか？次の方程式セットを考えてみましょう。

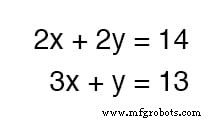
これらの2つの方程式を足し合わせることができますが、これは完全に有効な代数演算ですが、 x の値を取得するという目標にはメリットがありません。 および y ：

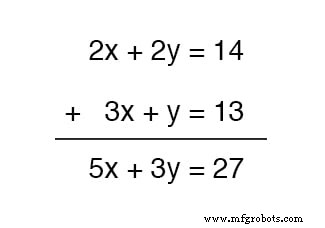
結果の方程式には、元の方程式と同じように2つの未知の変数が含まれているため、解を得ることができません。

ただし、方程式の1つを操作して、 の負の項を持つことができるとしたらどうでしょうか。 追加されたときに他の方程式のそれぞれの項をキャンセルしますか？

次に、システムは、最後の（偶然の）例と同じように、単一の未知の変数を持つ単一の方程式に還元されます。

y しか回せなかったら 下の方程式の項を -2y 2つの方程式を足し合わせたときに、両方が y になるように、 方程式の項はキャンセルされ、 x だけが残ります。 用語、これは私たちを解決策に近づけるでしょう。

幸いなことに、これを行うのは難しくありません。 掛ける -2 による下の方程式のすべての項 、それは私たちが求める結果を生み出します：

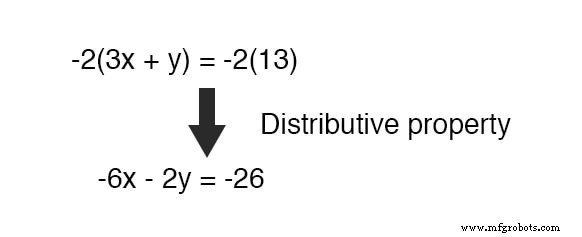
ここで、この新しい方程式を元の上の方程式に追加できます。

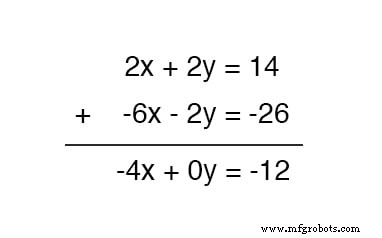
x を解く 、 3 の値を取得します ：

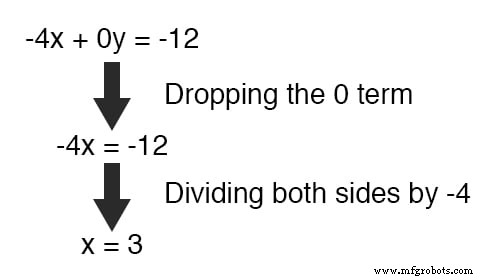
この新しく見つかった値を x に置き換えます 元の方程式の1つ、 y の値に 簡単に判断できます：

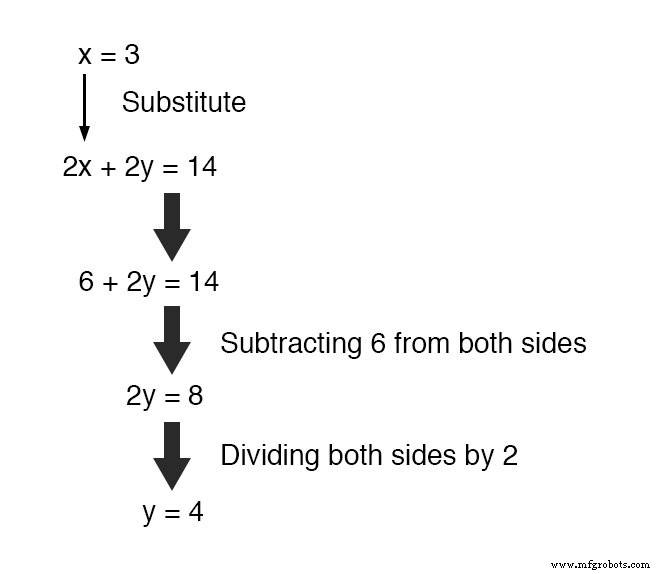
3変数システムでこのソリューション手法を使用するのは少し複雑です。

置換と同様に、この手法を使用して、3つの変数の3方程式システムを2つの変数を持つ2つの方程式に減らし、それを再度適用して、1つの未知の変数を持つ単一の方程式を取得する必要があります。

実例を示すために、置換セクションの3変数連立方程式を使用します。

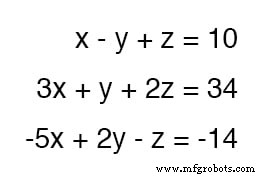
上の方程式の係数値は 1 であるため 変数ごとに、操作してキャンセルツールとして使用するのは簡単な方程式になります。

たとえば、 3x をキャンセルしたい場合 真ん中の方程式からの項、私たちがする必要があるのは、一番上の方程式を取り、その各項に -3 を掛けるだけです。 、次に次のように真ん中の方程式に追加します：

その -5x の一番下の方程式を取り除くことができます 同じ方法で項：元の上の方程式を取り、その各項に 5 を掛けます 、次に、その変更された方程式を一番下の方程式に追加し、 y のみの新しい方程式を残します および z 用語：

この時点で、同じ2つの未知の変数 y を持つ2つの方程式があります。 および z ：

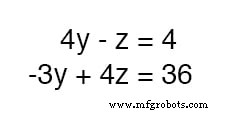
調べてみると、 -z 上の方程式の項を利用して、 4z をキャンセルできます。 上の方程式の各項に 4 を掛けるだけで、下の方程式の項 2つの方程式を足し合わせます：

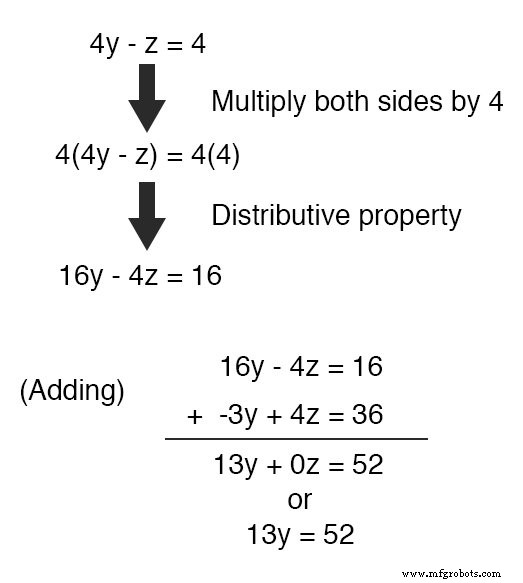
新しい方程式をとる 13y =52 y を解きます （両側を 13 で割ることにより ）、 4 の値を取得します y の場合 。

この値を 4 に置き換えます y の場合 2変数方程式のいずれかで、 z を解くことができます。 。

y の両方の値を代入する および z 元の3変数方程式のいずれかに代入すると、 x を解くことができます。 。

最終的な結果（代数のステップは、これまでに理解しているはずなので、割愛します！）は、 x =2 です。 、 y =4 、および z =12 。

関連するワークシート：

• 回路解析ワークシートの連立方程式