ブール代数

数値を足し合わせてブール代数の探索を始めましょう：

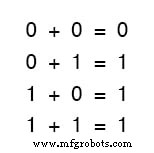
最初の3つの合計は、初歩的な足し算に精通している人には完全に理にかなっています。

ただし、最後の合計は、数学の基本原則に反しているように見えるため、デジタル電子機器の他のどの単一のステートメントよりも混乱の原因となる可能性があります。

まあ、それは実数の加算の原則と矛盾しますが、ブール数の場合は矛盾しません。

ブール代数の世界では、任意の量と任意の算術演算に対して可能な値は1または0の2つだけであることに注意してください。

ブール値の範囲内に「2」のようなものはありません。 「1+ 1」の合計は確かに0ではないため、消去法では1でなければなりません。

用語をいくつ追加しても、数が少なくてもかまいません。次の合計を考慮してください：

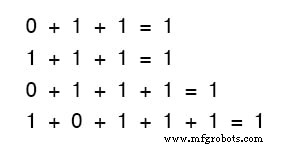
ORゲート

最初の方程式のセットの2項の合計をよく見てください。

そのパターンはあなたに馴染みがあるように見えますか？そうすべき！これは、ORゲートの真理値表に見られるのと同じ1と0のパターンです。

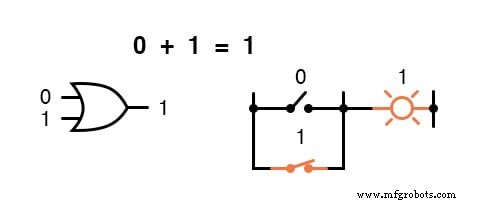
言い換えると、ブール加算は、「OR」ゲートの論理機能、および並列スイッチ接点に対応します。

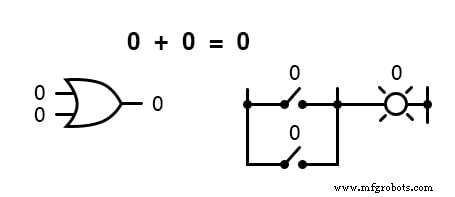
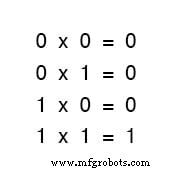
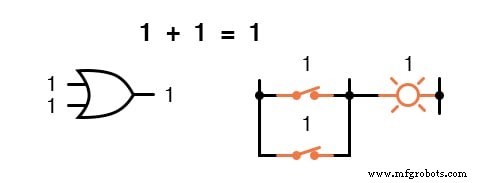
ブール数学の領域では、減算のようなものはありません。

減算は負の数の存在を意味します： 5-3 5 +（-3）と同じです 、およびブール代数では、負の量は禁止されています。

除算は実際には複合減算にすぎないため、ブール数学にも除算のようなものはありません。 、乗算が複合加算であるのと同じように 。

ANDゲート

乗算はブール代数で有効であり、ありがたいことに実数代数と同じです。 0 を掛けたものは何でも 0 です 、および 1 を掛けたもの 変更されません：

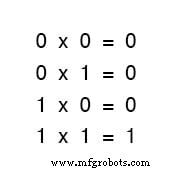
この一連の方程式もおなじみのように見えるはずです。これは、ANDゲートの真理値表にあるパターンと同じです。

つまり、ブール乗算は「 AND 」の論理関数に対応します。 」ゲート、および直列スイッチ接点：

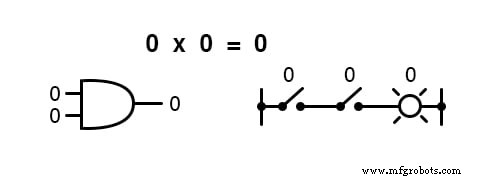
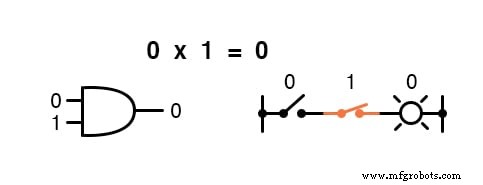
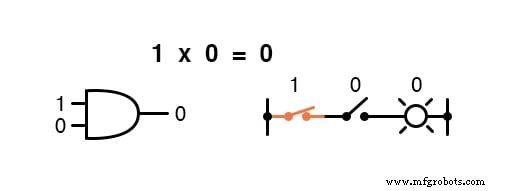
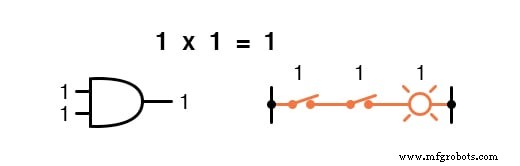
「通常の」代数と同様に、ブール代数は変数を表すためにアルファベット文字を使用します。

ただし、「通常の」代数とは異なり、ブール変数は常に大文字であり、小文字になることはありません。

2つの可能な値のうち、 1 のいずれか1つのみを所有することが許可されているため、 または 0 、すべての変数には補数があります ：その値の反対。

たとえば、変数「 A 」の値は 0 です 、次に A の補数 値は 1 。

ブール表記では、変数文字の上にあるバーを使用して、次のように補完を示します。

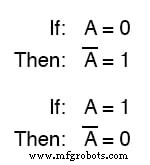
ゲートではありません

書面によると、「 A 」の補足 」は「 A-not 」または「 Aバー 」。補完を表すために「プライム」記号が使用されることがあります。

たとえば、 A ’は A を補完するものになります 、分数表記ではなく、微積分の微分を表すためにプライム記号を使用するのとほとんど同じです d / dt 。

ただし、通常、「バー」記号は「プライム」よりも広く使用されています。 」記号。この章の後半でさらに明らかになる理由があります。

ブール補完は、 NOTゲートの形式で同等性を検出します 、または通常閉のスイッチまたはリレー接点：

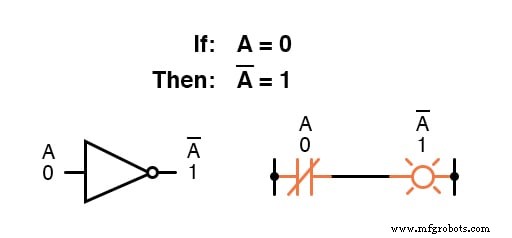
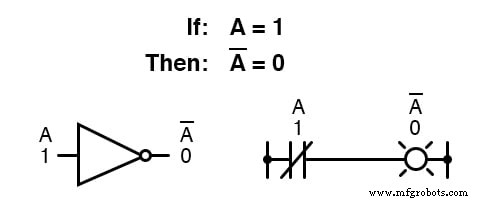
ブール量の基本的な定義により、加算と乗算の単純な規則が導き出され、有効な算術演算として減算と除算の両方が除外されました。

ブール変数とその補集合を表す記号があります。次のセクションでは、ブールIDの開発に進みます。

レビュー：

• ブール加算は OR と同等です 論理機能、および並列スイッチ接点。
• ブール乗算は AND と同等です 論理機能、および直列スイッチ接点。
• ブール補完は NOT と同等です 論理関数、および通常は閉じています リレー接点。

関連するワークシート：

• ブール代数ワークシート