ベン図のブール関係

4番目の例には A があります 部分的に重なっている B 。ただし、最初に下のすべてのハッチング領域全体を確認し、次に重複領域のみを確認します。以下に示すように、上の領域にいくつかのブール式を割り当てましょう。

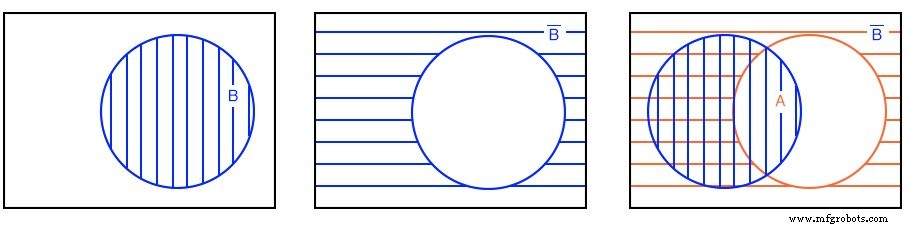
左下には、 A の赤い水平ハッチング領域があります 。 B には青い縦のハッチング領域があります 。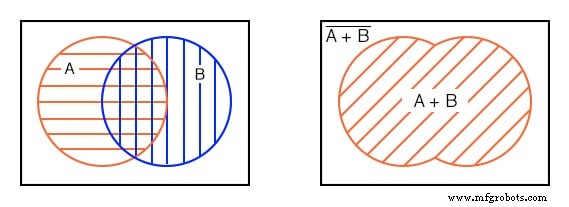

ハッチングのスタイルに関係なく、すべてのハッチングされた領域の合計である両方の領域全体を見ると、右上の図は包括的 OR に対応しています。 A、Bの関数。ブール式は A + B です。 。

これは45 ^o で示されます ハッチングエリア。ハッチングされた領域の外側はすべて（A + B）に対応します-ではありません 上に示すように。 4番目の例の次の部分に進みましょう。

円が重なっているベン図を見るもう1つの方法は、両方の A に共通する部分だけを見る方法です。 および B 、左下の二重ハッチング領域。 AND に対応するこの共通領域のブール式 関数は AB 右下に示すように。二重ハッチングされた AB 以外のすべてに注意してください AB-ではない 。

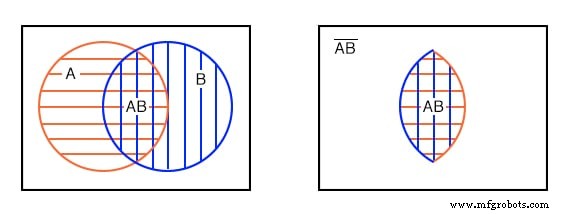
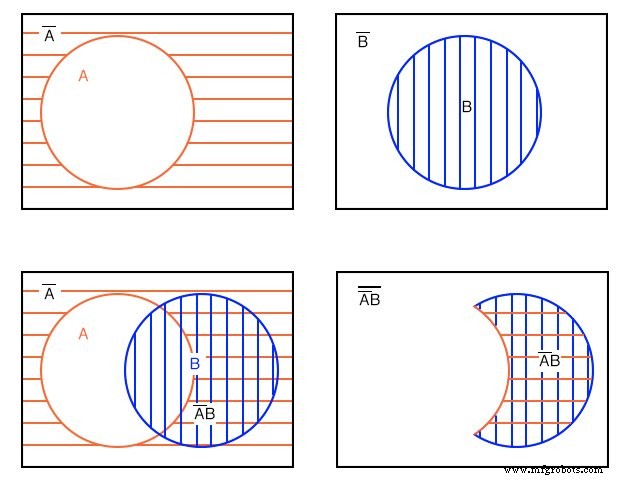
A のメンバーの一部に注意してください 、上記は（AB） ’のメンバーです 。 B のメンバーの一部 （AB） ’のメンバーです 。しかし、（AB） ’のメンバーは誰もいません 二重ハッチング領域内にある AB 。

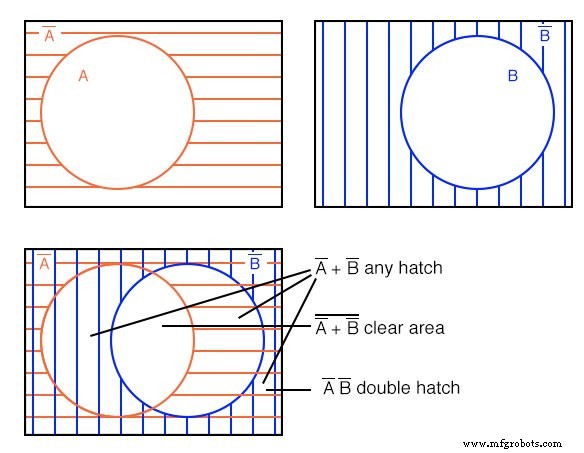
左上の2番目の例を繰り返しました。以前にスケッチした5番目の例は、比較のために右上に示されています。後で、カルノー図の別のグループに完全に含まれる、時折発生する要素または要素のグループを見つけます。

次に、補完された変数を含むブール式の開発を以下に示します。

例： （上）

A’B のベン図を表示する （A-AND Bではありません）。

解決策： 左上から始めて、赤い水平の陰影が付いた A ’ （A-not）次に、右上、 B 。次に、左下に、AND関数 A’B を作成します。 前の2つの領域を重ね合わせます。ほとんどの人は、これを例の答えとして使用します。

ただし、二重ハッチングされた A’B のみ わかりやすくするために右端に示されています。 A’B という表現 両方の A ’が存在する地域です および B オーバーラップ。 A’B の外側の明確な領域 は（A’B） ’ 、これは提起された例の一部ではありませんでした。

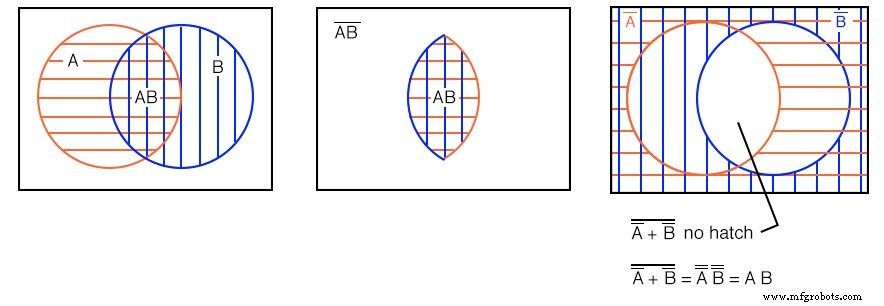
ブール値のまたはと似たようなものを試してみましょう 機能。

例： B ’+ A を検索

解決策： 右上は B から始めます これは B ’を補完するものです 。最後に、 A をオーバーレイします B ’の上に 。 またはの形成に関心があるため 関数では、ハッチングのスタイルに関係なく、すべてのハッチング領域を探します。したがって、 A + B ’ 右上のすべてのハッチング領域です。わかりやすくするために、左下に1つのハッチング領域として示されています。

例： （A + B ’）’ を検索

解決策：

緑の45 ^o A + B ’ ハッチングされた領域は、前の例の結果です。 toに移動します。（A + B ’）’ 、左上の現在の例では、 A + B ’の補集合を見つけましょう。 、これは、（A + B ’）’ に対応する左上の白い透明な領域です。 。

右側で、 AB ’を繰り返していることに注意してください。 結果と比較するために、前の例の二重ハッチングの結果。 （A + B ’）’ に対応する地域 および AB ’ 左上と右上はそれぞれ同じです。これは、ド・モルガンの定理と二重否定で証明できます。

これはポイントをもたらします。ベン図は実際には何も証明しません。正式な証明にはブール代数が必要です。ただし、ベン図は検証と視覚化に使用できます。ベン図を使用して、ド・モルガンの定理を検証および視覚化しました。

例：

ブール式 A ’+ B’ は何ですか ベン図のように見えますか？

解決策： 上の図

赤の水平ハッチング A ’から始めます 青い縦のハッチング B ’ その上。図のように図を重ね合わせます。まだ A ’を見ることができます 他のハッチに重ねられた赤い水平ハッチ。また、 B の一部であったものも入力します （B-true）円、ただし B のその部分のみ A に共通しない白丸 白丸。

B ’だけを見ると 青い縦のハッチ、開いている A のその部分を埋めます B に共通しない円 。タイプに関係なく、ハッチがまったくないリージョンは、 A ’+ B’ に対応します。 。つまり、中央の空白以外のすべてです。

例：

ブール式（A ’+ B’） ’は何ですか ベン図のように見えますか？

解決策： 図の上、左下

中央の白い広場を見ると、すべてがそうではありません A ’+ B’ の以前のソリューションで 、これは（A ’+ B’） ’ 。

例： （A ’+ B’） ’=AB であることを示す

解決策： 図の下、左下

以前、右上の図で、白い開いた領域が（A ’+ B’） ’であることを示しました。 。以前の例では、 AB の交差点（オーバーレイ）に二重ハッチング領域を示しました。 。これは、ここで繰り返される左と中央の図です。

2つのベン図を比較すると、この開いた領域、（A ’+ B’） ’ 、二重ハッチング領域 AB と同じです （AおよびB）。 （A ’+ B’） ’=AB であることも証明できます 上記のように、ド・モルガンの定理と二重否定による。

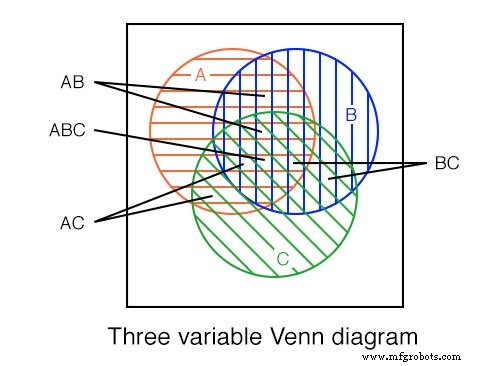
リージョン A を含む上記の3変数ベン図を示します。 （赤い水平）、 B （青い縦）、および、 C （緑45 ^o ）。真ん中の部分では、ブール式 ABC を表す3つの領域すべてが重複していることに注意してください。 。

A が存在する大きな花びらの形をした領域もあります および B ブール式 AB に対応するオーバーラップ 。同様の方法で A および C オーバーラップ生成ブール式 AC 。そして B および C オーバーラップ生成ブール式 BC 。

上記のAND式で記述された領域のサイズを見ると、領域のサイズは、関連付けられたAND式の変数の数によって異なることがわかります。

• A 、1-変数は大きな円形の領域です。
• AB 、2変数は小さな花びらの形をした領域です。
• ABC 、3変数は最小の領域です。
• AND項の変数が多いほど、領域は小さくなります。