金電極間のγ-グラフェンナノリボンのスピン依存輸送特性に関するひずみ調査

はじめに

電荷とスピンは、電子の2つの主要な固有の特性です[1,2,3]。従来のマイクロエレクトロニクスは、電子のスピン状態に関係なく、電子の電荷特性に集中することがよくあります。また、電界[4、5]を導入して半導体材料の電子輸送を制御し、情報の輸送や処理を実現する方法が一般的になっています。科学技術の継続的な進歩により、大規模集積回路の実験は以前よりもますます増えています[6]。電子および小型化の高密度コンポーネントが緊急の必要性になっています。ここ数十年で、科学者はスピントロニクス上の分子デバイスへの電子のスピン特性を調査し始めました[7、8]。スピンの緩和時間は比較的長く、スピンデバイスの欠陥や不純物の影響を受けにくく、電場や磁場などの一連の手段で実現できます[9]。したがって、分子接合のスピントロニクス特性に関する多くの変調法が集中的な研究の焦点となっています。

化学ドーピング[10,11,12]や電磁場制御[13、14]と比較して、ひずみ工学[15,16,17]は、ナノ材料にとって最も効果的で制御可能な技術であると考えられています。格子と電子の間の相互作用（スピン、軌道など。 ）ひずみ工学によって誘発される材料の電気的、磁気的、または光学的特性に影響を与え、他の独特の物理的または化学的効果の出現につながる可能性があります[18、19]。さらに、ひずみは必然的に実験サンプル準備の過程にあり、これはさまざまなチャネルによって適用される可能性があります。たとえば、基板がスムーズに準備されていない[20]、サンプルと基板材料の格子定数が一致していない[21]、またはナノリボンのエッジにクリンプが存在する[22]などです。

さらに、ひずみが2次元（2D）材料の電子構造に明らかな影響を与えることが報告されています[23、24]。一軸ひずみを加えると、グラフェンのディラックコーンのシフトが観察され[25]、大きな範囲の一軸ひずみはグラフェンのゼロバンドギャップを変化させる可能性があります[26]。さらに、最近の研究では、ひずみ工学がシリコンナノワイヤの輸送特性を改善するための効率的な方法であることが示されています[27]。黒リンナノリボンの単層にひずみを加えると、キャリアの輸送方向も変化し、キャリア移動度の異方性を制御できます[28]。さらに、ひずみは半導体のスピン特性に影響を与える可能性があります。隆起したバブリング構造に関してひずみを加えることにより、グラフェンに谷分極電流を生成することができます[29]。ひずみによって引き起こされるバンド収束は、フォスフォレンの熱電性能を向上させる効果的な方法である可能性があります[30]。さらに、ナノ接合の光学的特性[31]および磁気的特性[32]も、ひずみによって誘発および変調される可能性があります。したがって、材料のひずみ工学の規制が価値があることを理解することは難しくありません。

近年、炭素科学は分子接合の発展分野に広く影響を与えています[33,34,35,36]。クロスカップリング反応を採用することにより、Li et al 。 [37]は、銅の表面にグラフジインサンプルを合成することに成功しました。それ以来、graphdiyneは国際的な研究者から大きな関心を集めてきました[38、39]。グラフェンは、ベンゼン環とアセチレン結合とのC–C結合の共役によって形成される、2D平面ネットワーク構造を持つグラフェンの同素体です[14、40、41、42、43、44、45]。単純な階層化された sp と比較して ² グラフェンの軌道混成構造[46]、グラフェンは sp を保持します および sp ² 混成状態で、その独特の分子構造がより複雑であると判断します。 α-グラフィン[40、41]、β-グラフィン[47]、γ-グラフィン[42、48、49]、α-2-グラフィン[14]、6など、graphyneファミリーに属する多くの既存のメンバーがあります。 6,12-グラフィン[43]、14,14,14-グラフィン[44]、δ-グラフィン[45]など。それらの既存の構造の中で、γ-グラフィンはフェルミ準位の周りにディラックコーンのような電子構造を持っていません。これはグラフェンとはかなり異なります。グラフェンナノリボンと同様に、γ-グラフィンもアームチェアとジグザグγ-グラフィンナノリボン（AγGYNおよびZγGYN）にカットできます。スピンフィルタリング、負の差抵抗などの優れた性能を観察するために、ZγGYNに広範な研究が展示されています。ただし、金電極間のZγGYNに実装されたひずみの研究は報告されていません。

ZγGYNのひずみ工学の利点を探求することを目的として、ZγGYNに基づく分子接合部にひずみを導入し、第一原理計算を使用して研究を実行します。この論文では、最初に、さまざまな磁気構成内のZγGYNの電子構造に焦点を当てました。観察は、スピン分裂の現象が接合部にひずみを導入した後に発生することを示しました。これは、ひずみがスピンを操作する手段である可能性があることを意味します。さらに、接合部のスピン電流に関する結果は、ひずみがデバイスの輸送特性にある程度重要な影響を及ぼしていることを示しています。そして、ひずみ工学は、電極と中間散乱領域の間の結合を強化し、電子チャネルを広げることができることを発見しました。

モデルとメソッド

図1では、3つの異なる分子接合がそれぞれM1、M2、M3として示されています。接合部は、左電極、散乱領域、右電極の3つの部分に分けることができます。ここでは、延性と導電性に優れているため、電極材料として金（Au）ナノワイヤーを使用します。 Au電極は（111）表面で劈開されます。そして、散乱領域は、いくつかの繰り返されるZγGYNユニットで構成されています。鉛のAu原子と中央部の炭素（C）原子は硫黄原子でつながっています。グラフェン接合の実験では、透過型電子顕微鏡（TEM）内で高エネルギー電子照射を使用することにより、実験でグラフェンナノリボンを分子デバイスとして調整して多くの構造に切断できることが示されています[50]。グラフェンと同様に、ZγGYNに基づく分子デバイスもこの方法で接続できる可能性があります。 M1はひずみを伴って導入されておらず、図1aに示すように、散乱領域は平坦です。 M2は x で湾曲しているように見えます U の軸 -横方向のひずみが原因で、図1bで平坦でなくなった湾曲した構造。構造が最も複雑なM3システムの場合、 S を保持します。 -湾曲した構造。 M3の散乱領域におけるZγGYNの元の長さは、M1のそれの2倍です。したがって、ひずみ効果のあるZγGYNは、+ x の反対方向に曲げることができます。 および− x 軸、 S を提示する -図1cの湾曲した構造。図1e、fのM1〜M3の側面図は、図1a〜cの散乱部分の主な図に対応しています。詳細なジャンクションは、次の写真から見ることができます。

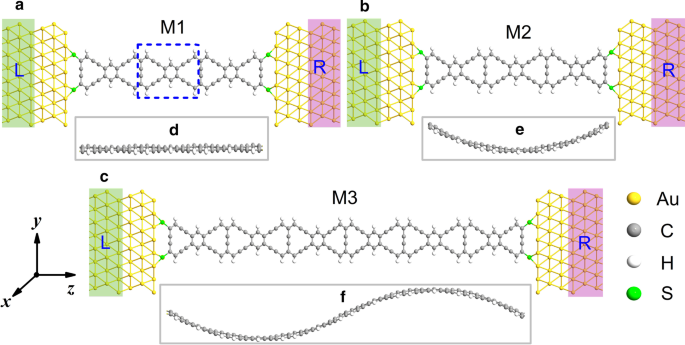
（オンラインカラー）分子接合モデルの概略図は a として表示されています M1、 b M2と c M3、その散乱領域はそれぞれフラット、カーブ（U字型）、ダブルカーブ（S字型）です。パネル a の青い破線の長方形 格子定数が12.297ÅのZγGYNRの繰り返しユニットセルを寄付します。わかりやすくするために、 d の散乱領域の側面図 M1、 e M2と f a に対応するM3 – c 展示もされています。 L / Rは左/右電極を表します

まず、Atomistix ToolKitパッケージで密度汎関数理論計算を実装することにより、設計されたユニットセルと分子構造を最適化します[51、52]。最適化の結果によると、ユニットセルの格子定数は図1aで約12.297Å、M1-M3の散乱領域の長さは図1a〜cで約36.891Å、35.473Å、70.559Åです。 M1-M3の場合、金と硫黄原子間の結合長は2.38Å、硫黄と炭素原子間の結合長はそれぞれ1.84Å、1.62Å、1.92Åです。詳細な計算パラメータは以下のように設定されています。交換補正ポテンシャルは、汎関数のPerdew–Burke–Ernzerhによる一般化された勾配近似として使用されます[53]。静電ポテンシャルのメッシュカットオフエネルギーは150Ryで、フェルミ関数の温度は300Kに設定されています。各原子にかかる力は0.02eV /Åと小さくなっています。さらに、1×1×100のMonkhorst–Packメッシュが選択され、電子密度の収束基準は10 ^-5 です。 総エネルギーのeV。さらに、周期的な画像間の相互作用を回避するために、計算では少なくとも20Åの真空層の厚さが設定されています。エネルギーの関数としての透過スペクトル（ E ）およびバイアス電圧（ V ）は次のように定義されます

ここで、\（G ^ {{{\ text {R}}（{\ text {A}}）}} \）は、中央散乱領域の遅延（高度）グリーン関数\（\ Gamma _ {{\ text { L（R）}}} \）は、左（右）電極とσの結合行列です。 =±1は電子のスピンアップ/スピンダウンを提供します。スピン輸送電流は、Landauer-Büttikerの式[54、55]

ここで、\（\ mu _ {{\ text {L（R）}}} \）と\（f _ {{\ text {L（R）}}} \）は、電気化学ポテンシャルと、左側の対応するフェルミ分布関数です。 /右電極、それぞれ。デバイスの状態密度（DDOS）は、\（D \ left（E \ right）=-\ frac {1} {\ pi} {\ text {Im}} G ^ {{\ text {R}}で計算できます。 }（E）\）。

結果と考察

ジグザグγ-グラフィンユニットセルのバンド構造は、それぞれ図2a〜cに示すように、非磁性（NM）、強磁性（FM）、および反強磁性（AFM）の状態でプロットされています。計算の進歩では、上端と下端に付着した炭素原子の磁性はすべて同じ方向に設定され、FM状態に近づきます。 AFM状態の設定は反対です。 ZγGYNRはNM状態では金属であり、エネルギーバンドは図2aのフェルミ準位を通過します。 NMと同様に、FM状態のZγGYNRも金属ですが、明らかなスピン分裂が見られます。図2bでは、スピンアップ方向のエネルギーバンドがダウンシフトされ、スピンダウンバンドがアップシフトされています。ただし、ZγGYNRをAFM状態に設定すると、バンド構造は0.55 eVの小さなバンドギャップを示し、図2cの半導体になります。さらに、状態の対応する総エネルギーも、それぞれM1〜M3について計算されています。相対的な結果は次のように表示されます。NM状態のZγGYNRユニットセルのエネルギーは-3524.42090eVの最高値であり、AFM状態のZγGYNRユニットセルのエネルギーは-3524.49299eVの最低値です。最高エネルギーと最低エネルギーのエネルギー差は約0.07eVです。したがって、すべてのエネルギーのデータによれば、AFM状態はZγGYNRの基底状態であるという結論を導き出すことができます。 ZγGYNRのFM状態は、ナノリボンのスピン偏極を誘発する可能性があり、スピントロニクスの分野で適用されます。以下では、3つのジャンクションの深い輸送メカニズムについて説明しました。

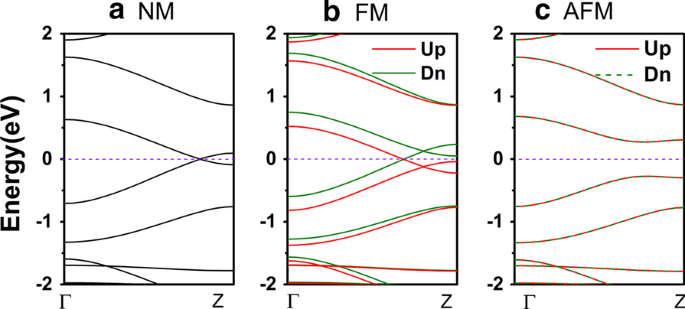
（オンラインカラー）ZγGYNRのバンド構造は a 内に示されています NM、 b FM、および c それぞれAFM状態。フェルミ準位はゼロと見なされています

まず、図3にゼロバイアスでの3つの接合部の透過スペクトルをプロットします。図3aには、透過スペクトルの鋭いパルスのピークが多数あり、フェルミ準位の近くに小さなバンドギャップがあります。これはM1が半導体であることを示しています。 。したがって、適切な電圧の影響下で、炭素原子間に形成されたC =CまたはC≡C結合が電子輸送のためのコンダクタンスチャネルを提供するため、電子は左から右の電極を通過することができます。図3bのM2の歪みデバイスの場合、その透過スペクトルはM1の透過スペクトルとまったく同じではありません。フェルミ準位の周りを移動する透過ピークはまだたくさんあります。つまり、ひずみの影響を受けたM2の透過ピークはM1の透過ピークよりも広くなります。さらに、透過ピークはすべてフェルミ準位に近づいているようです。この現象は、M2の散乱領域への歪みの影響から発生し、Au電極と中間ZγGYNR間の結合が強化され、M1よりも伝送チャネルが広くなります。

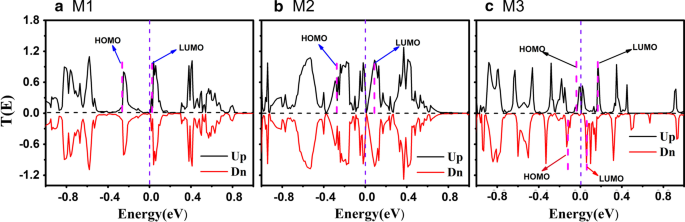
（オンラインカラー）ゼロバイアスでのスピン依存透過スペクトルは、 a で示されています。 M1、 b M2と c それぞれM3。スピンアップとダウンの透過係数は、正（黒）と負（赤）の値に設定されています。一方、分子投影された自己無撞着ハミルトニアンの分布はここに示されています

さらに、M3の場合、図3cに示すように、最も明白な特徴は、スピンアップ（黒い実線）とスピンダウン（赤い実線）の透過ピークが縮退していないスピン分割です。さらに、M3の透過ピークはM1の透過ピークと同じくらい鋭いですが、同様に密度が高くなります。スピンアップ透過ピークはフェルミ準位を前方に移動しますが、スピンダウン透過スペクトルは図3cで大きな透過ギャップを示しているため、M3はスピン分離しているように見えます。これは、M3のS字型とひずみ効果の両方の組み合わせによって説明できます。 S字型の歪みにより、M3の電荷分布が変化し、元の電気双極子が破壊されたため、M3の接合部が磁気的挙動を示し、スピン分裂現象が見られます。明らかに、M3のZγGYNRはM1の2倍の長さであり、電極と散乱領域の間の相互作用はM2よりも弱くなります。ただし、非対称の S のため -形状構造、ZγGYNRはもはや同じ平面にないため、 sp が変更される可能性があります および sp ² γ-グラフィンのハイブリッドコンポーネント。したがって、M3は新しい分子接合を設計するためのより完璧なモデルです。

図3a、bの透過ピークの詳細を注意深く比較することにより、M1には透過ピークがなく、M2には-0.02eVのエネルギーで非常に鋭いピークがあることを確認することが非常に重要です。 M1とM2の違いを深く理解するために、図4a、bに示すように、デバイスの局所状態密度（DLDOS）を-0.02eVで描画します。図4aのM1の場合、電子は主に金の電極に局在し、電子雲はZγGYNRの領域にあまり分布していないことに注意してください。したがって、M1の電荷輸送用の伝送チャネルは少なくなります。しかし、M2の場合、電子は電極とリボン全体のZγGYNRの散乱領域に密に分布しており、電子伝達のために豊富な伝送チャネルが提供されていることを示しています。したがって、M2の透過スペクトルはフェルミ準位付近でM1よりも広く見えます。この結果は、M2とひずみ制御の分子接合がより優れた輸送特性を保持することを意味します。これについては後で説明します。

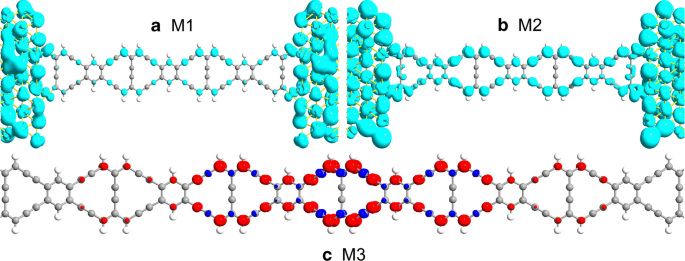
（オンラインカラー）− 0.02eVのエネルギーでのDLDOSは a として表示されています M1と b それぞれM2。等値は0.01Å ^-3 と見なされます ・eV ^-1 。 c M3のスピン密度等値面も展示されており、赤と青の色はそれぞれスピンアップ成分とスピンダウン成分を表しています。等値は0.015Å ^-3 と見なされます ・eV ^-1

さらに、各モデルに対応するDDOSを図5a〜cに示します。ここで、緑（オレンジ）の実線はそれぞれスピンアップ（-ダウン）方向を表しています。まず、図5a〜cのDDOSの形状と分布は、図3a〜cに示す透過スペクトルに対応しています。図3aのM1のDDOSは、 E で鋭いピークを示します> 0であり、スピンアップおよびスピンダウンDDOSはゼロ点に対して対称です。図3bのM2の場合、DDOSのピークはフェルミ準位全体にほぼ広がり、分子接合の電荷輸送に寄与しています。したがって、M2に実装されたひずみは、フェルミ準位で一緒にピーク移動を促進します。 DDOSのピーク構造と透過スペクトルの類似性は、ZγGYNRのエネルギーレベルと透過スペクトルの間に明確な対応があることを示しています。歪みによって引き起こされるAu電極とZγGYNRの間の結合は、伝送トンネルを大幅に拡張します。

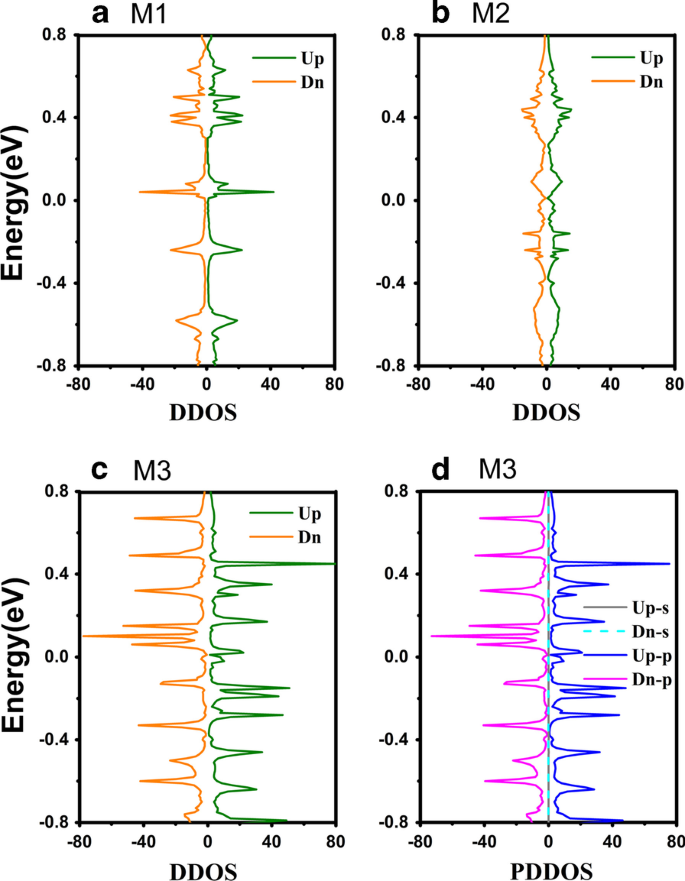
（オンラインカラー）DDOSは a として表示されます M1、 b M2と c それぞれM3。 d M3の予測デバイス状態密度（PDDOS）です。 「Up-s」と「Dn-s」は s- の略です スピンアップおよびダウン方向の軌道PDDOS、「Up-p」および「Dn-p」は p- を表します それぞれスピンアップ方向とダウン方向の軌道PDDOS

透過スペクトルとDDOSからわかるように、M3のスピン分裂現象は図5cでも観察でき、ZγGYNRの長い分子鎖を持つM3が磁性を帯びていることを示唆しています。 M3の磁性を直感的に理解できるように、スピン密度の分布を図4cにプロットします。ここで、赤と青の色はそれぞれスピンアップ成分とスピンダウン成分を表しています。図4cでは、原子の磁気モーメントが主にナノリボンの中心に局在し、中心から端に向かって徐々に弱くなる傾向を示していることがわかります。ジグザググラフェンナノリボンと同様に、ZγGYNRは磁性を帯びていることが知られています[56]。ただし、歪みが存在するため、電極と中央領域の間の結合により、元の磁気分布が変化します。したがって、電極に最も近い原子の磁性は消え、電極から最も遠い中央領域の磁性は残ります。どの軌道がほとんどの磁気の原因であるかを判断するために、図5dにM3のPDDOSをプロットします。 PDDOSから、 s- 軌道電子は、図5dの中央でゼロ値になる傾向があるため、M3の磁性にはほとんど寄与しません。つまり、M3の磁性は主に p-に依存します。 ピークの形状と位置の両方が図5cのDDOSと非常に一致しているため、軌道電子。したがって、外部電子の寄与は、M3の電荷輸送における内部電子の寄与よりもはるかに大きくなります。 M1-M3の輸送特性を表示するために、電流-電圧（ I-V ）特性は以下で調査されました。以前の予測を検証するために、相対的な内部メカニズムが明らかになりました。

すべてのシステムのさまざまなパフォーマンスに対応するメカニズムをさらに調査するために、 I–V を計算します。 図6aに示すように、提案されたM1〜M3の曲線。図6aは、計算されたスピン依存の I–V 各デバイスに適用されたバイアスの関数としての曲線とインサート図6a 'は、計算された総電流を示しています。電圧範囲が-0.6Vから0.6Vに増加すると、図6aに示すように、電流曲線は正と負のバイアス電圧範囲で対称的に動作します。 M2とM3の電流はM1の電流よりも明らかに大きいことに注意してください。これは、ひずみが電荷輸送に一定の影響を与えることを示しています。ひずみのないM1の電流の大きさは、3つの接合部の中で最小です。バイアス電圧が増加するにつれて、ゆっくりと増加します。さらに、バイアス電圧の増加に伴い、傾きが最大のM2の電流が急激に増加していることがわかります。特に、M2の電流は同じバイアス電圧でのM1の電流のほぼ3倍です。対照的に、S字型に湾曲した構造のM3の電流は、M1とM2の間で中程度であり、M2よりも伝導性が弱いが、M1よりは強い。

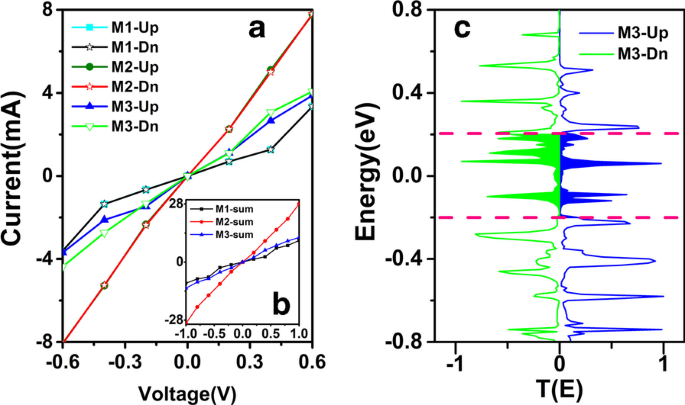
（オンラインカラー） a 計算されたスピン依存の I–V M1、M2、およびM3に適用されたバイアスの関数としての曲線。挿入図（a '）は、各デバイスの計算された合計電流を示しています。 b バイアス− 0.04 VでのM3のスピン依存透過スペクトル。ピンクの点線の間の影付きの領域は、電流に寄与するエネルギー領域、つまりバイアスウィンドウです（右側と左側の影付きの青と緑の領域は、それぞれスピンアップとスピンダウンします。）

また、図6aのM3の電流からもスピン分裂現象が見られます。 I–V 曲線は、上記の透過スペクトルおよびDDOSと完全に一致しています。ひずみによって分子が同じ平面に存在しなくなり、非局在化共役π-が損傷することは間違いありません。 ZγGYNRの結合。しかしながら、圧搾効果により、電極と散乱領域との間の結合が強化され、最終的に電子チャネルが広がり、電流が増加するという、考慮すべき別の側面があります。したがって、M3の電流もひずみの影響を受けますが、M2の電流ほどではありません。以下の理由が考えられます。散乱領域の長さは、Au電極とZγGYNRの間の結合をある程度減少させ、M3の電流をM1よりも大きく、M2よりも小さくします。ひずみ効果とZγGYNRの長さは、一般的にM3の電流強度を決定します。したがって、図6aのM3にはスピン依存電流が現れることがわかります。これは、図5cにも対応しています。上記の計算結果はすべて、ひずみのあるM3にスピン分裂現象があることを示していますが、実際にはそれほど重要ではありません。スピン変調の場合、他のより効率的な手段があるかもしれません。実際、電場[57、58]、エッジ修正[59]、ドーピング[60]などの他の方法も、多くの2次元ベースのナノデバイスでスピン偏極を誘発し、スピン分裂を促進する可能性があります。

結果から、M3はスピン分裂現象を保持していることがわかり、バイアス電圧が-0.4 Vの場合、スピンアップとスピンダウンの電流値の差を見つけるのは難しくありません| I _上 – _dn | M3が最大で、図6aの青と緑の実線からわかります。この目的のために、図6bに-0.4バイアスでのM3の透過スペクトルをプロットします。ここで、青と緑の実線は、それぞれスピンアップ成分とスピンダウン成分を示しています。バイアスウィンドウの緑色の部分の透過領域が青色の透過領域よりも大きいことがわかります。その結果、対応するスピンダウンの電流は、同じバイアス電圧-0.4Vでのスピンアップの電流よりも大きくなります。

図3bの透過スペクトルに関しては、フェルミ準位付近のM2の透過ピークが-0.02 eVに現れることがわかっているため、フロンティア分子軌道が電荷輸送に大きな役割を果たします。さらに、以前の計算結果は、M1とM2の電流がスピンに依存しないことを示しているため、M1とM2のスピンダウン方向の分子投影自己無撞着ハミルトニアン（MPSH）の空間分布はここでは無視されます。図7aのM1の最高被占軌道（HOMO）の空間分布は、図7bのM2の空間分布よりも弱いです。 M2のHOMOは散乱領域全体で十分に非局在化されており、その結果、ここでM2の最大電流が発生することがわかります。 M3の場合、スピンアップHOMOは図7cのZγGYNRの両側に分布しますが、最低空軌道（LUMO）は主に図7dの中央領域に局在します。逆に、歪んだZγGYNRの磁性により、スピンダウン方向のHOMOの波動関数は図7eの中央領域に局在しますが、図7fのLUMOの分布はHOMOの分布と似ています。スピンアップ方向。 MPSHの空間分布は特定の領域に比較的局在しており、M3の電流が小さいことを示しています。言い換えれば、分子軌道の相互作用は、複雑で柔軟な原子相互作用と外部効果の組み合わせに依存します。

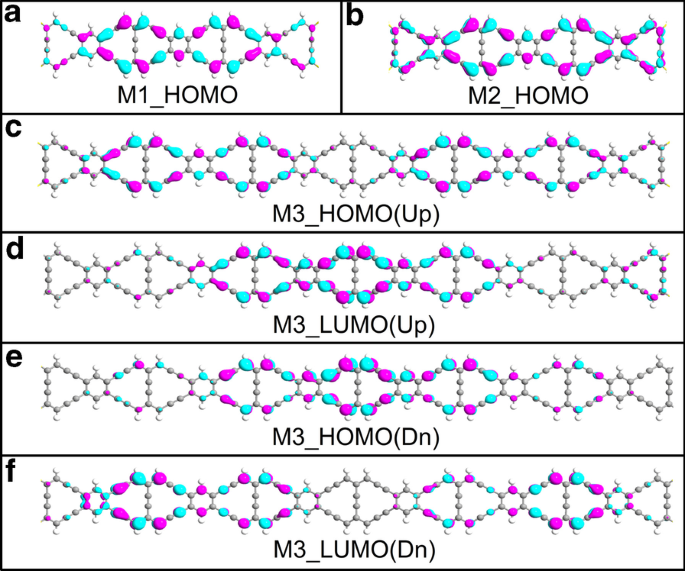
（オンラインカラー） a のHOMO M1と b スピンアップ方向のM2; c – f 異なるスピン方向におけるM3のHOMOとLUMOの空間分布

結論

要約すると、ZγGYNRに基づくひずみ接合の電子構造と輸送特性が研究および分析されました。我々の結果は、設計されたZγGYNRのAFM状態が基底状態であり、FM状態のバンド構造がスピン分裂していることを示しています。さらに、このひずみは分子接合の輸送特性に重大な影響を及ぼします。同じ長さで、ひずみはAu電極とZγGYNRの間の軌道結合を大幅に強化します。その結果、M2の電子チャネルが広がるため、M2の電子伝達挙動はM1の電子伝達挙動よりもはるかに大きくなります。さらに、ZγGYNRの長さと方向は、接合部の輸送特性に一定の影響を及ぼします。具体的には、長さが長くなることにより、Au電極とZγGYNRの結合が弱くなるため、M3の電流はM2の電流よりも小さくなります。さらに、M3の磁気分布は、明らかなスピン分裂現象を引き起こします。輸送特性の対応するメカニズムは、透過スペクトル、LDDOSなどの観点から説明されています。私たちの結果は、次世代のフレキシブル電子デバイスに新たなアイデアを提供する可能性があります。

データと資料の可用性

分子接合の設計と計算計算は、AtomistixToolKitパッケージによって実行されました。

略語

γ-GYNR：

γ-グラフェンナノリボン

2D：

二次元

NM：

非磁性

FM：

強磁性

AFM：

反強磁性

DDOS：

デバイスの状態密度

DLDOS：

デバイスの局所状態密度

PDDOS：

予測されるデバイスの状態密度

MPSH：

分子投影された自己無撞着ハミルトニアン

HOMO：

最高被占軌道

LUMO：

最も低い空軌道

上：

スピンアップ

Dn：

スピンダウン