第一原理研究からのSiAsおよびSiAs2単分子層におけるひずみ調整可能なバンドギャップと高いキャリア移動度

背景

原子的に薄い2次元（2D）結晶は、現代の材料科学で最も急速に急成長している分野の1つになっています。用途の広い電子特性、優れた電子移動度、およびナノエレクトロニクスとオプトエレクトロニクスの有望なアプリケーションにより、物性物理学者の大部分が新しい2D材料を探すようになっています。グラフェン[1–4]に続いて、シリセン[5–7]、窒化ホウ素ナノシート[8、9]、遷移金属ジカルコゲナイド（TMD）[10、11]、黒リン[12、13]、ボロフェン[14–16]、アルセネン[17、18]、テルレン[19]、およびそれらの等電子化合物[20–23]。 2D材料のリストは急速に拡大しており、電子およびその他の特性の全範囲を網羅する、数千種類を超えるそのような材料が現在知られています。そして、それらのバルクの対応物とは異なる、またはそれよりも優れたそれらの新しい特性は、理論的に予測され、実験的にしっかりと確認されています。

すでにバンドギャップまたは他の望ましい特性を持っているものを含む多様な2D材料を見つけるために大規模かつ実質的な努力が投資されましたが、コンセンサスは得られていません。優れたキャリア移動度、高い機械的安定性、および質量のないディラック電子を備えたグラフェンは、これまで多くの注目を集めてきましたが、固有のバンドギャップがないため、現代の電子デバイス業界での応用が妨げられています。多大な努力が払われてきたが、副作用なしにかなりのバンドギャップを開くことは達成されていない[24、25]。オプトエレクトロニクスデバイスで高性能のTMDは、確かに固有のバンドギャップを持っていますが、キャリア移動度が低くなっています[26–28]。歪みに敏感な調整可能なバンドギャップと異方性の高いキャリア移動度を持つ黒と青のリンは、空気中で安定に保つことができません[13、29]。最近、層状SiAsとSiAs ₂ の合成 単結晶が実現されており[30–32]、機械的に剥離しても層構造がほとんど得られないことを示しています。

本研究では、第一原理密度汎関数理論計算（DFT）に基づいて、動的および熱力学的に安定な2つの半導体単分子層SiAsおよびSiAs ₂ を提案しました。 。それらは両方とも間接バンドギャップ（それぞれ2.39eVと2.13eV）を持っています。 2つの面内方向に沿って等方性ひずみを加えると、SiAs（SiAs ₂ ）が実質的に変形します。 ）直接ギャップ1.75 eV（1.60 eV）材料への単分子層。さらに、SiAsとSiAs ₂ 単分子層は、MoS ₂ よりもはるかに高いキャリア移動度を持っています 黒フォスフォレンのような異方性輸送を表示し、オプトエレクトロニクスへの応用の可能性を秘めています。私たちの作品は、光学デバイスの新しい機能のためのナノスケールでの新しい道を切り開きます。

計算方法

DFT計算は、Vienna ab initioシミュレーションパッケージ（VASP）コード[33]を使用して実行されます。一般化勾配近似（GGA）の下でPerdew-Burke-Ernzerhof（PBE）[34]交換相関汎関数を使用しました。電子-イオン相互作用を説明するために、プロジェクター拡張波（PAW）法[35]が採用されました。層間の相互作用を避けるために、シートに垂直に（c軸に沿って）20Åの真空を適用しました。平面波基底関数系には、500eVの運動エネルギーカットオフが使用されます。ブリュアンゾーンのサンプリングは、2Dシート用の15×5×1 Monkhorst-Pack [36]グリッドを使用して実行されます。電子的自己無撞着緩和とイオン緩和の両方に採用された収束基準は、10 ^-4 に設定されています。 エネルギーと力はそれぞれ0.01eV /Åです。フォノン計算は、PHONOPYコード[37、38]を介してスーパーセル法を使用して実行され、スーパーセルの実空間力定数は、VASPに実装されている密度汎関数摂動理論（DFPT）で計算されます。さらに、より厳密なエネルギー（10 ^-8 eV /原子）および力の収束基準（10 ^-4 eV /Å）は、振動スペクトルの計算中に使用されます。分子動力学（MD）計算では、（3×3×1）スーパーセルが使用され、モル-体積-温度（NVT）アンサンブルで2fsの時間ステップで6psの間温度が300Kに保たれます。ラマンスペクトルは、CASTEPコード[39–41]を使用して理論のPBEレベルで計算されました。

結果と考察

緩和された自立型2DSiAsおよびSiAs ₂ の幾何学的構造と電子密度分布 はそれぞれ図1a、bに示され、それらのバルク構造は追加ファイル1：補足資料の図S1に示されています。追加ファイル1：図S1aおよびbに示すように、バルクSiAs（SiAs ₂ ）はC2 / m（Pbam）対称性を持ち、3.06Å（1.66Å）の距離でファンデルワールス力によって弱く結合された積み重ねられたSi-As層で構成されます。単層SiAsのユニットセルは菱形であり、その最適化された結晶パラメータは a です。 ₁ =3.69Åおよび b ₁ =10.83Å（φ） =99.81°。 SiAsには、6個のSi原子と6個のAs原子が含まれています。各Si原子には4つの最も近い隣接原子（3Asと1Si）がありますが、各As原子は隣接するSi原子と3つの共有結合のみを形成します。 Si–Si結合とSi–As結合の2種類の結合が存在します。また、Si–Si結合長は約2.35Å、Si–Asの結合長は2.39Åから2.43Åの範囲であり、座屈した高さは d です。 ₁ =4.86Å。単層SiAsの側面図では、眼鏡のひも状のような構造が、二重層と単層が交互にかさばって形成されています。シリコンとヒ素化合物のもう1つの単分子層構造は、SiAs ₂ です。 。そのプライムセルには、4つのSi原子と8つのAs原子が含まれ、長方形の構造を持ち、最適化された結晶パラメータは a です。 ₂ =3.68Åおよび b ₂ =10.57Å。各As原子には3つの最も近い隣接Si原子があるか、隣接するSi原子と1つの共有結合を形成し、2つの共有結合を形成しますが、各Si原子には4つの最も近い隣接するAs原子しかありません。前者とは異なり、SiAs ₂ Si–Si結合の代わりに弱いAs–As結合（2.50Å）を所有しています。また、そのSi–As結合は2.41Åから2.45Åの範囲であり、座屈した高さは d です。 ₂ =5.09Å。電子密度分布から、As原子は電気陰性度が大きいためにSi原子から電子を引き付け、電子密度が大きくなります。将来の実験的特性評価を支援するために、バルクおよび単分子層のSiAsおよびSiAs ₂ のラマンスペクトルをさらに計算して確認しました。 。単分子層と完全な結晶の間の明確なシフトは、追加ファイル1：補足資料の図S2に見られます。その起源は、層ファンデルワールス相互作用の影響として特定されています[42]。

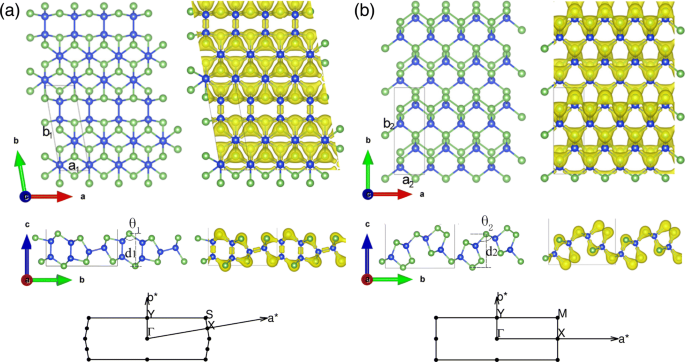
単分子層SiAsおよびSiAs ₂ の幾何学的構造と電子密度分布 。 （オンラインカラー）単分子層の上面図と側面図 a SiAsと b SiAs ₂ 幾何学的構造と電子密度分布および関連するブリルアンゾーン。青と緑のボールは、それぞれSi原子とAs原子を示しています

SiAsの安定性を学ぶために（SiAs ₂ ）、最初に E として定義される凝集エネルギーを計算しました。 _coh =（ nE _Si + mE _As − E _モノ ）/（ n + m ）、ここで E _Si 、 E _As 、および E _モノ は、単一のSi原子、単一のAs原子、および単分子層SiAsの1つの式単位（SiAs ₂ ）の合計エネルギーです。 ）、それぞれ、n（m）は式単位のAs（Si）原子の数です。私たちの計算によると、SiAs単分子層の凝集エネルギーは5.13 eV /原子であり、SiAs ₂ よりも少し大きいです。 単分子層4.98eV /原子。比較のために、同じ理論レベルで、アルセネンとシリセンの凝集エネルギーは、それぞれ2.99と3.71 eV /原子です[18、43]。 SiAsとSiAs ₂ の高い凝集エネルギー 両方が高い安定性で強く結合していることを明らかにします。

単分子層SiAsおよびSiAs ₂ の構造安定性をさらに確認する 、振動フォノンスペクトル計算も実行しました。図2aに示すように、Γ付近の横音響モードを除いて、正の周波数がモードの大部分を占めています。 これはフォノンの軟化によるものであり、他の同様のシステムで報告されており[44、45]、構造が両方とも動的に安定していることを示しています。次に、室温（ T ）で6psの第一原理MDシミュレーションを実行しました。 =300 K ）、図2bに示すように。わずかなエネルギー変動と手入れの行き届いた構造は、それらが室温で熱的に安定していることを示唆しています。私たちの結果は、単分子層SiAsとSiAs ₂ 室温で実験的に実現できます。

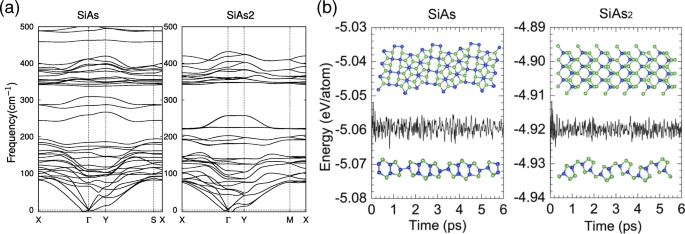
単分子層SiAsおよびSiAs ₂ のフォノン分散曲線とMDシミュレーション 。 a 単分子層SiAsおよびSiAs ₂ のフォノン分散曲線 。 b SiAsおよびSiAs ₂ の室温MDシミュレーション中の総エネルギーと時間の関係 。 6psの終わりの単層構造の選択されたスナップショットも提供されます

単分子層SiAsおよびSiAs ₂ の最適化された構造 、今、私たちはそれらの電子的性質に注意を払います。 SiAsおよびSiAs ₂ の計算された軌道分解バンド構造 単分子層を図3に示します。私たちの計算では、SiAsとSiAs ₂ が明確に示されています。 単分子層は両方ともバンドギャップの広い間接半導体です。単層SiAの場合、価電子帯の最大値（VBM）は Y にあります。 ポイント、伝導帯の最小値（CBM）はΓにあります （図3a）。単分子層SiAsの間接バンドギャップは E です。 _g =PBEスキーム内で1.72eV。 Y でのVBMの状態もわかります。 ポイントは p で構成されます _y 軌道、ΓのCBM ポイントは主にs軌道で構成されます。これは、以下に示すように、外部変形が2つの状態に異なる影響を及ぼし、間接-直接遷移につながる可能性があることを意味します。 SiAsとは異なり、単層SiAs ₂ は、 Y の側面にVBMが配置されたほぼ直接的な半導体です。 ポイントとCBMはそれから少しずれています（図3b）。 SiAs ₂ 単層の間接バンドギャップは E です _g =PBEスキーム内で1.42eV。そして、SiAs ₂ のVBMとCBM 単層は p で構成されています _y それぞれ軌道とs軌道。より正確なバンドギャップ値を取得するために、SiAsとSiAs ₂ の混成汎関数計算（HSE06）[46、47]も実行しました。 単層。計算されたバンド構造（図3a、bの右側）から、PBEとHSEからのバンド状態のシャープは基本的に同じであり、間接バンドギャップは混成汎関数計算内で予測されますが、ギャップ値はSiAsおよびSiAs ₂ では2.39eVおよび2.07eVに増加 それぞれ。

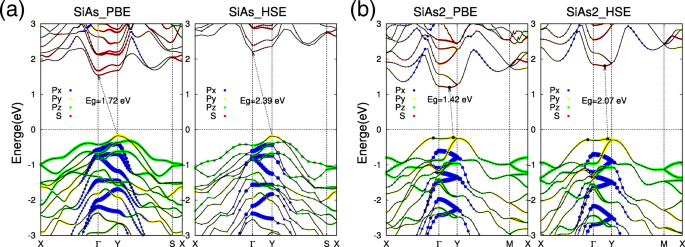
単分子層SiAsおよびSiAs ₂ のバンド構造 PBEとHSE06によって計算されます。単分子層SiAsおよびSiAs ₂ のバンド構造の電子軌道分解 a として表されます および b 、 それぞれ。赤い点は s を示します 軌道、青、黄、緑は p _x 、 p _y 、および p _z 、 それぞれ。フェルミ準位はゼロに設定され、点線で示されます

新たに発見された2D材料の最新の電子デバイスにおける潜在的なアプリケーションの重要な要素であるキャリア移動度は、CBMとVBMのバンドギャップと位置と同じくらい重要です。 SiAsおよびSiAs ₂ の電子構造特性の詳細を取得するには 次に、単分子層について、室温（ T ）での変形ポテンシャル（DP）理論[48]に基づいて、音響フォノン制限キャリア移動度（x方向とy方向の両方の電子と正孔を含む）を計算しました。 =300 K ）。低エネルギー領域（300 K ）、電子-音響-フォノン散乱がキャリア輸送を支配します。これにより、音響フォノン制限が、MoS ₂ などの多くの2D構造のキャリア移動度を予測する効果的な方法になります。 単分子層[49]、テルレン[19]、閃光[50]、および数層のMoO ₃ [51]。計算された有効質量 m ^∗ およびキャリア移動度μ SiAsとSiAsの ₂ 単分子層は、両方とも高移動度であり、黒色フォスフォレンのように異方性を輸送することを示しています（追加ファイル1：表S1および図S3とS4を参照）[50]。 SiAsおよびSiAs ₂ のキャリア移動度を推定するには 、最初に、ほとんど自由な電子モデルを使用してバンドのフィッティングを実行し、有効なキャリア質量を取得しました。 SiAの場合、 x を定義します および y 格子ベクトルに垂直な方向として b および a 、 それぞれ。 x方向に沿った\（m_ {e} ^ {*} \）と\（m_ {h} ^ {*} \）は約0.15 m ₀ および0.86 m ₀ 、それぞれ、y方向に沿って0.80 m ₀ および0.22 m ₀ （ m ₀ は自由電子質量）です。 SiAs ₂ の場合 、格子ベクトルの方向 a x として定義されます 、 b の y 。 x方向に沿った\（m_ {e} ^ {*} \）と\（m_ {h} ^ {*} \）は約0.14 m ₀ および0.65 m ₀ 、それぞれ、y方向に沿って2.05 m ₀ および1.82 m ₀ 、 それぞれ。さらに、弾性定数（C）と変形ポテンシャル（E1）を調べました（追加ファイル1：図S2およびS3を参照）。上記で得られた m に基づく ^∗ 、CおよびE1の値から、表1に示すようにキャリア移動度を推定しました。SiAs（SiAs ₂ の電子移動度 ） x に沿って および y 方向は0.66（0.26）および0.54（0.11）×10 ³ ・ cm ² V ^-1 S ^-1 、 x に沿った穴の可動性 および y 方向は3.90（0.13）および0.30（0.65）×10 ³ ・ cm ² V ^-1 S ^-1 、それぞれ、MoS ₂ よりもはるかに高い [49]。

単分子層SiAsおよびSiAs ₂ のSiおよびAs原子の基本的な結合メカニズムにさらに光を当てる 、PBE汎関数を使用したそれらの全体および部分状態密度（PDOS）は、VBMおよびCBMに対応する電子密度分布とともにそれぞれ図4に示されています。 AsおよびSi原子のPDOS（図4a、c）は、 s の強い混成軌道を示していることがわかります。 および p 軌道、それらの間の強い共有結合を示します。単分子層SiAsとSiAs ₂ の違い p のローカリゼーションです _z As原子の異なる結合配位環境に起因する軌道。 SiAsとSiAsの両方のAs原子に局在する孤立電子対の電子状態 ₂ 単分子層は、最も近い3つの結合軌道を補強して、単分子層構造の座屈形成を決定し、 p を形成します。 _z 軌道ローカライズアクション。単分子層SiAsでは、孤立電子対はSi–As結合によって分離されており、反発効果を緩和して p を広げます。 _z 軌道。一方、単分子層のSiAs ₂ 、As–As結合は、V族半導体で非常に一般的な状況のままで、 p をローカライズします。 _z より深いエネルギー準位での軌道。

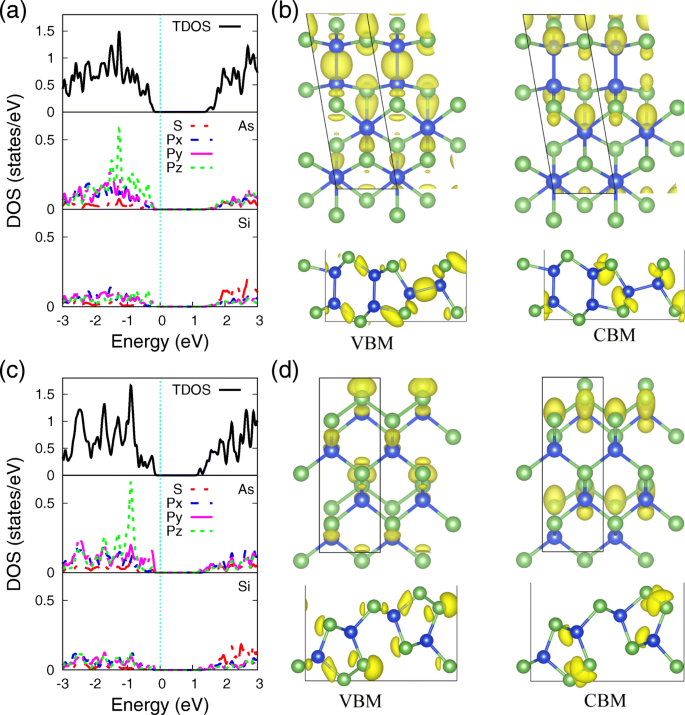
予測される状態密度とVBMおよびCBMの電子密度。 AsおよびSi原子の投影状態密度（PDOS）と、（ a のVBMおよびCBMに対応する電子密度分布） 、 b ）SiAsおよび（ c 、 d ）SiAs ₂ 単層。等値面値0.034 e /Å ³

私たちが知っているように、フロンティア状態の特徴は、伝導チャネルの微視的理解だけでなく、最適な接触の設計にも大きな関心を持っています。[52]単分子層SiAsおよびSiAs ₂ のVBMおよびCBMに対応する電荷密度 それぞれ図4bとdに示されています。 VBMはほぼSiとAsの3p軌道の混成軌道ですが、CBMは主にSiとAsの3s軌道の寄与によるものであり、図4a、cのPDOSの結果およびバンド構造の電子軌道分解とも一致しています。図3で

機械的ひずみは、2D材料の電子特性を変調する効果的な方法であり、黒と青のフォスフォレンやその他のナノシート材料のバンド構造を変更するために広く使用されています[53–55]。特に、座屈構造システムの場合、エネルギーコストは通常​​非常に小さく、著しいひずみを引き起こします。ここでは、幾何学的最適化中に各原子の格子定数と内部自由度を変化させることにより、機械的ひずみの適用をシミュレートします。ひずみε εとして定義されます =（ l − l ₀ ）/ l ₀ 、ここで l および l ₀ は、単分子層SiAsおよびSiAs ₂ の歪んだ平衡格子定数です。 。図5a、bでは、2DSiAsおよびSiAs ₂ の高座屈幾何学的構造の詳細なバリエーション ひずみの下でそれぞれ表されます。座屈角度θを変更することにより、座屈した高さが膨張または圧縮されていることがわかります。 _1（2） ほぼ線形の変化で二軸圧縮または引張ひずみを伴う。また、それらの高い座屈幾何学的構造は両方とも非常に大きなひずみの下で良好に保たれ、そのフォノンスペクトルは、追加ファイル1：図S5およびS6に示すように、大きなひずみ領域でも負の周波数が存在しないこともわかりました。単分子層SiAsとSiAs ₂ のギャップ変動 二軸圧縮および引張ひずみ下をそれぞれ図5c、dに示します。 SiAsとSiAs ₂ の電子特性がわかります。 ひずみに敏感に依存し、特定のひずみ領域で間接的に直接バンド遷移を起こし、次に大きなひずみ領域で金属に遷移します。

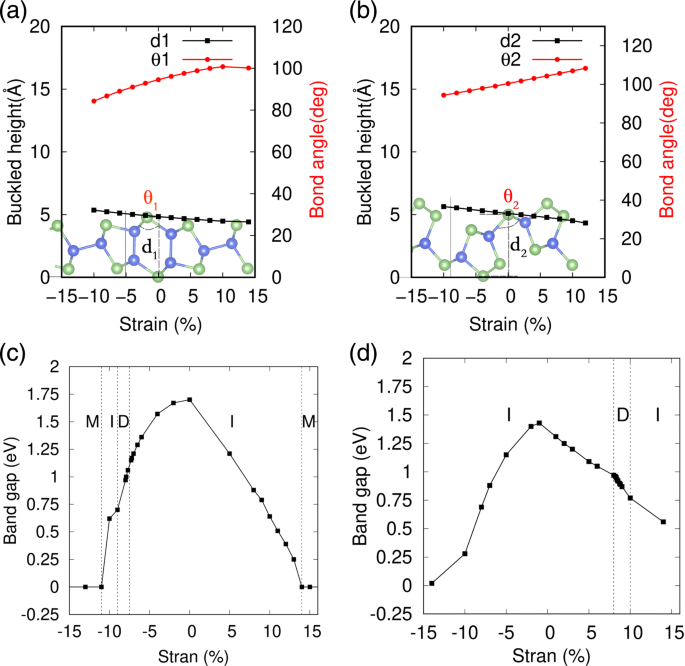
2DSiAsおよびSiAs ₂ の幾何学的構造とバンドギャップに対するひずみの影響 。 a 、 c SiAsを表します。および b 、 d SiAs ₂ を示します; M、I、およびDは、それぞれ金属、間接半導体、および直接半導体を表します

SiAsとSiAs ₂ の詳細なバリエーション バンド構造を図1および2に示します。それぞれ6と7。二軸圧縮ひずみ下では、単分子層SiAsの座屈高さが増加し、CBMがΓからシフトします。 Y–S線上の点に移動し、Yに戻ります。圧縮ひずみがεに達するまで、VBMはY点に静止したままです。 =− 10 ％ 。したがって、圧縮ひずみが増加すると、バンドギャップは間接YからΓに切り替わります。 、間接Yを介してY–S線上の点に、YをYに向け、Γ上の間接点に戻る 図6に示すように、–Y線からYへ。引張ひずみの場合、YのVBMはY–S線上の点に移動し、CBMはΓに移動します。 Yに移動し、バンドギャップは間接のままです。図5cに示すように、大きなひずみの場合、圧縮または引張に関係なく、金属転移が発生します。

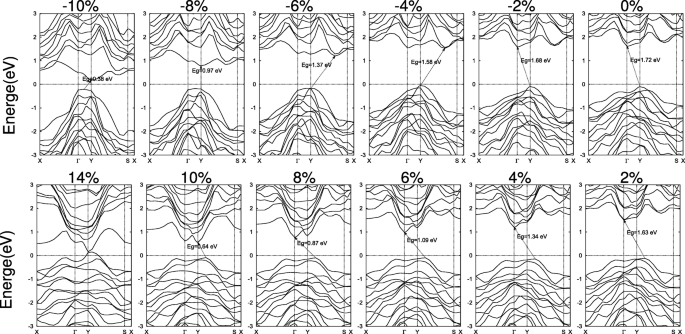
二軸ひずみ下の2DSiAのバンド構造。フェルミ準位はゼロに設定され、点線で示されます

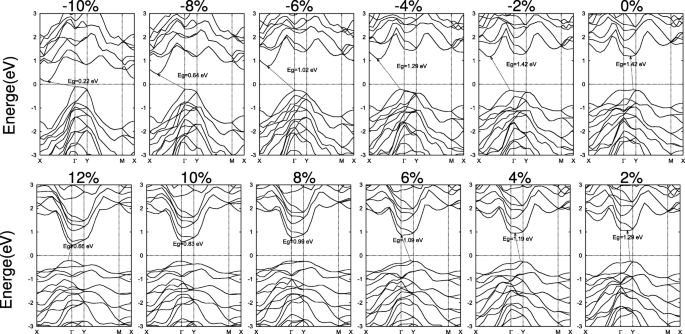
2D SiAs ₂ のバンド構造 二軸ひずみの下で。フェルミ準位はゼロに設定され、点線で示されます

図7では、2D SiAs ₂ についても同様の研究が行われています。 。圧縮の代わりに、8〜10％の範囲の引張ひずみにより、直接バンドギャップが生じます。単分子層SiAs ₂ 引張ひずみ下で座屈高さが減少するにつれて広がり、VBMはΓ上の点からシフトします。 –y行からΓ そして、8〜10％の範囲にとどまり、Γ上のポイントにシフトします。 –X線、CBMがΓ上の点から移動している間 –y行からΓ 待ってください。したがって、引張ひずみが増加すると、バンドギャップはΓで間接から切り替わります。 –y線でΓを指示します – Γ 次に、Γ上のポイントを間接的に戻します。 –x行からΓ 、図7に示すように、圧縮ひずみは間接バンドギャップのままです。また、大きなひずみは同様の効果をもたらし、SiAsと同様の金属転移を引き起こします。

歪んだSiAsおよびSiAs ₂ の代表的な直接バンド構造 追加ファイル1：図S7aおよびbにも、PBEおよびHSEの計算で示されています。 SiAsの場合、 E の直接バンドギャップ _g =1.75 eV （HSE） Y にローカライズされたVBMとCBM ポイントは、εの2軸圧縮ひずみの下で取得されます。 =− 7.5 ％ 。 SiAsとは異なり、εの二軸引張ひずみ =8.5 ％ SiAs ₂ を誘導します E の直接バンドに _g =1.60 eV （HSE）。そして、VBMとCBMはΓにあります ポイント。

結論

要約すると、第一原理DFT計算を実行して、シリコンとヒ素化合物の2つの新しい種類の2D材料、SiAsとSiAs ₂ を提案しました。 、動的および熱力学的に安定しています。私たちの計算によると、SiAsとSiAs ₂ 単分子層は、2.39 eV のバンドギャップを持つ間接半導体です。 および2.07 eV 、 それぞれ。 SiAsとSiAs ₂ のバンドギャップ 単分子層はひずみに敏感であり、ひずみは間接から直接のバンド遷移を経て、特定の機械的ひずみによって金属にさえも影響を受けます。 SiAsおよびSiAs ₂ 単分子層はMoS ₂ よりも高い移動度を持っています 黒フォスフォレンのような異方性輸送を表示します。私たちの作品は、光学デバイスの新しい機能のためのナノスケールでの新しい道を切り開きます。

略語

2D：

二次元

CASTEP：

ケンブリッジシーケンシャルトータルエネルギーパッケージ

CBM：

伝導帯の最小値

DFT：

密度汎関数理論

DFPT：

密度汎関数摂動理論

DP：

変形ポテンシャル

GGA：

一般化された勾配近似

MD：

分子動力学

NVT：

モル-体積-温度

PAW：

プロジェクター拡張波

PBE：

Perdew-Burke-Ernzerhof

PDOS：

部分状態密度

TMD：

トランジトン-金属ジカルコゲニド

VASP：

ウィーンabinitioシミュレーションパッケージ

VBM：

価電子帯の最大値