スピンに依存しないプラズモニックレンズ

はじめに

三次元（3D）自由空間では、集束、イメージング、光フーリエ変換（FT）など、光の流れを成形する上で光学レンズが不可欠な役割を果たします。しかし、従来のレンズに固有の限界も徐々に明らかになります。光の回折により、焦点の最大値の半分での横方向の半値幅は、波長の約半分以上になりますλ /（2 n 罪α ）、これは超解像リソグラフィーと顕微鏡学の実現を妨げる[1,2,3]。前面と背面の焦点面間の光学的FT関係に関しては、変換の速度はレンズの厚さと焦点距離によって制限されます[4]。とりわけ、光の波長と比較して、レンズの体積は、段階的な位相蓄積を達成するために使用される曲面のためにかさばります[5、6、7]。そして、それは研究やアプリケーションにおける小型で統合された光学デバイスの需要の高まりと両立しません[8,9,10]。

二次元（2D）金属/誘電体界面に沿って伝播するフォノンと電子振動のハイブリッドモードである表面プラズモンポラリトン（SPP）は、上記の制限を克服するための効果的なツールになります[11、12、13、14、15、16、 17]。サブ波長機能を使用すると、SPPをサブ波長スポットに簡単に焦点を合わせることができます[18、19、20、21]。 3D空間の光学レンズに対応するものとして、半円形スリットプラズモンレンズはSPPフィールドの焦点を合わせるだけでなく、2D平面ではるかに高速なSPPFTを実行します[4]。また、SPPを効果的に励起するために、スリットの幅は入射光の波長よりも狭くなっています。それにもかかわらず、半円形スリットによって生成されたSPPの集束は、入射光のスピン状態に強く依存します[22、23、24、25]。左円偏光（LCP）および右円偏光（RCP）の入射光の場合、SPPの焦点はスピン依存の横方向シフトを経験します。これは、自由空間での円偏光の集束とは異なります。 Hasmanらによる2008年のスピン依存半円形SPPレンズの研究以来。 [22,23,24]、スピン依存SPPフォーカシングを達成するためにさまざまなメカニズムが提案されています[26,27,28]。基本原理は、サブ波長スリットの配向角を操作することによって達成されるスピン依存の位相分布に依存しています。さらに、スピン依存SPP励起[29]、SPP渦[30]、SPPホログラム[31]、SPPベッセルビーム[32]、およびSPPエアリービーム[33]が実証されています。全体として、スピン依存SPPデバイスは広く研究されてきました。単一のサブ波長スリットまたはホールによって励起されたSPPでさえスピン状態に依存するため、励起光のスピン状態がSPPデバイスの機能に影響を与える可能性があることは明らかで正常です[24、26、28、33]。しかし、逆に、SPPフィールドへのスピン状態の影響を回避し、SPPレンズをスピン非依存にすることは可能ですか？

半円形スリットによって生成されたSPPには、スピン依存のスパイラル位相exp（iσ _± θ ）、ここでスピン状態はσ _± =±1はそれぞれLCPおよびRCPライトを表します[22、23、24、25]。本論文では、スパイラル位相の影響を排除し、スピンに依存しないSPPフォーカシングを実現するためのグローバルアプローチとローカルアプローチを提案します。グローバルアプローチは、半円形スリットを完全に処理し、逆スパイラル位相を導入できる反対の半円形スリットを追加することによってスパイラル位相をキャンセルします。サブ波長スリットの構成としての半円形スリットに関しては、スパイラル位相は、スリットの配向角度を変更することによって調整されるパンチャラトナム-ベリー位相と局所的に釣り合うことができます。スピンに依存しないSPPフォーカシングは、数値シミュレーションだけでなく、SPPのホイヘンス-フレネル原理を使用して分析および検証されます。提案されたアプローチの堅牢性は、半円形スリットの半径、中心角、および形状を変更することによってテストされます。以前のスピン依存SPPデバイス[26,27,28,29,30,31,32,33]と比較して、ここでのSPPの集束は、励起光のスピン状態から独立しているため、SPPの安定性を向上させることができます。レンズ。

結果と考察

二重半円形スリットで構成されるスピンに依存しないプラズモンレンズ

左円偏光（LCP）および右円偏光（RCP）の入射光で照らされた半円スリットプラズモニックレンズの場合、スパイラル位相は0からπに増加します。 図1bに概略的に示されているように、それぞれ反時計回りと時計回り。スパイラル位相は、円偏光と異方性ナノスケール構造の間の相互作用から生じます[23]。円偏光は、水平偏光と垂直偏光をπで合成したものです。 / 2位相差。 2つの線形成分によって励起されたSPPは、sin θとして表すことができます。 およびcos θ 、それぞれ[25]。したがって、円偏光によって生成されるSPPフィールドはsin θです。 + exp（iσ _± π / 2）cos θ =exp（iσ _± θ ）。スパイラル位相がないと、SPPの波面は半円形スリットとSPP波数ベクトル k に平行になります。 _sp 半径方向に沿ったものになります。ただし、スパイラル位相はスパイラル波面に対応し、SPP波数ベクトルは、図1aの赤と青の矢印で示されているように、半径方向からずれます。そして、最終的に、スパイラル位相は、SPPフォーカスの横方向のシフトをもたらします[22、23、25]。スピン非依存SPPレンズを実現するには、スピン制御SPPフォーカシングの原点であるスピン依存スパイラル位相を排除する必要があることは明らかです。

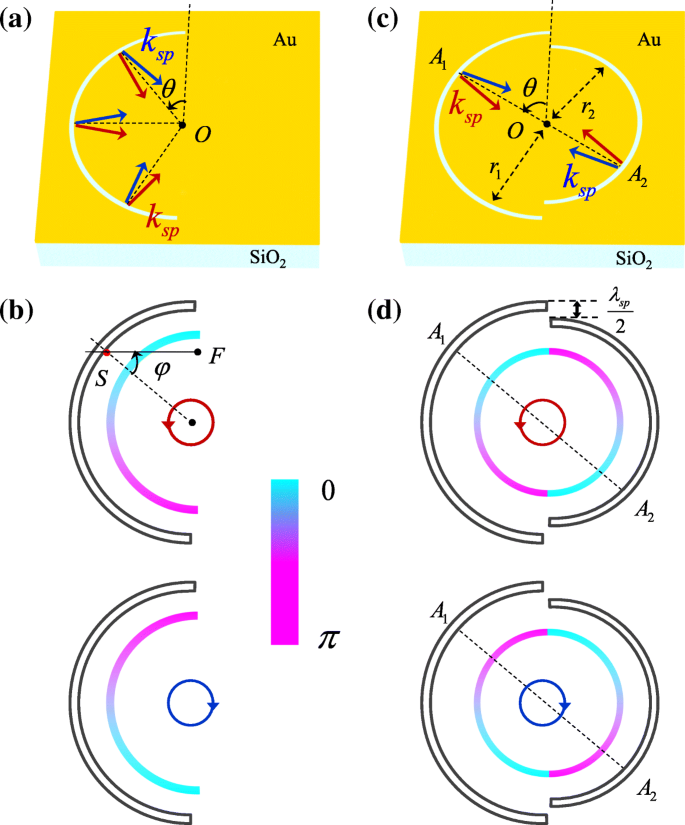
半円形スリットプラズモンレンズの概略図（ a ）およびスピンに依存しないSPPレンズは、2つの半円形スリット（ c ）で構成されていました。 ）。 LCPおよびRCP光の照射により、励起されたSPPはスピン依存のスパイラル位相を経験します（ b ）。別の半円形スリットを追加すると、余分なスパイラルフェーズが導入される可能性があり、 r の場合、2つのスパイラルフェーズが互いに打ち消し合う可能性があります。 ₁ − r ₂ =λ _sp / 2（ d ）

追加のスパイラル相を導入するために別の半円形スリットを追加することが解決策になる可能性があります。 2つの半円形スリットが同じ側にある場合、2つのスパイラルフェーズは互いに打ち消し合うことはできません。したがって、半円形のスリットを反対側に追加する必要があります。図1cは、半径 r が異なる2つの半円形スリットで構成されるSPPレンズの構造を概略的に示しています。 ₁ および r ₂ 。左右の半円形スリットに沿った励起されたSPPフィールドは、対応して次のように表すことができます。

πが存在します 2つの半円形スリットによって生成されるスパイラル位相間の位相差。特に、半径がΔ r を満たす場合 = r ₁ − r ₂ =λ _sp / 2、 k _sp Δ r =π πを補うだけで 2つのスパイラル位相間の位相差。図1dに示すように、SPPの対応する位相は中心対称です。具体的には、点 A から生成されたSPPの位相 ₁ 対称点 A から生成されたSPPの位相と同じです。 ₂ 。そして、 A によって生成されたSPP ₁ および A ₂ 中央で建設的に干渉するので、半円形のスリットに沿った他のポイントも干渉します。したがって、2つの半円形スリットによって生成されたSPPは、横方向にシフトすることなく中央に集束されます。入射光のスピン状態が変化すると、左右のスパイラル位相が同時に反転し、中心対称のままになります。したがって、LCPとRCPの両方の光によって励起されたSPPは、半円の中心に焦点を合わせることができます。これは、プラズモンレンズのスピンに依存しない特徴を示しています。

スピンに依存しないプラズモンレンズの性能は、SPPのホイヘンス-フレネル原理を使用して分析的に調べられます[34、35]。極座標系では、左右の半円形スリットによって生成されるSPPフィールドは、それぞれ次のように表すことができます。

ここで、φ 半径方向とSPP伝搬経路の間の角度を示し、 d 二次光源から任意の点までの距離 F 、図1bに示すように。式を代入します。 （1）と式。 （2）式に（3）と式。 （4）、SPPフィールド分布を取得でき、図2a〜dに示されています。白い破線の半円は半円形のスリットを表し、水平の破線はSPPの焦点の横方向のシフトを明確に示すために描かれています。 SPPフォーカスの横方向のシフトの方向は、左右の半円形のスリットでは常に反対であることがわかります。スピンに依存しないプラズモニックレンズの場合、SPP分布は、2つの半円形スリットによって生成されたSPPフィールドの重ね合わせであり、\（{E} _ {\ mathrm {sp}} \ left（\ rho、\ theta \ right）={E} _ {\ mathrm {sp}} ^ {\ mathrm {L}} \ left（\ rho、\ theta \ right）+ {E} _ {\ mathrm {sp}} ^ {\ mathrm {R}} \ left（\ rho、\ theta \ right）\）。したがって、中央のSPPの強度は

ここで、位相差はΔΦ _sp = k _sp （ r ₁ − r ₂ ）− π および用語π 左右のスパイラル位相の違いから生じます。スピンに依存しないフォーカシングを実現するには、SPPが中央で建設的に干渉する必要があります。したがって、スリットの半径は

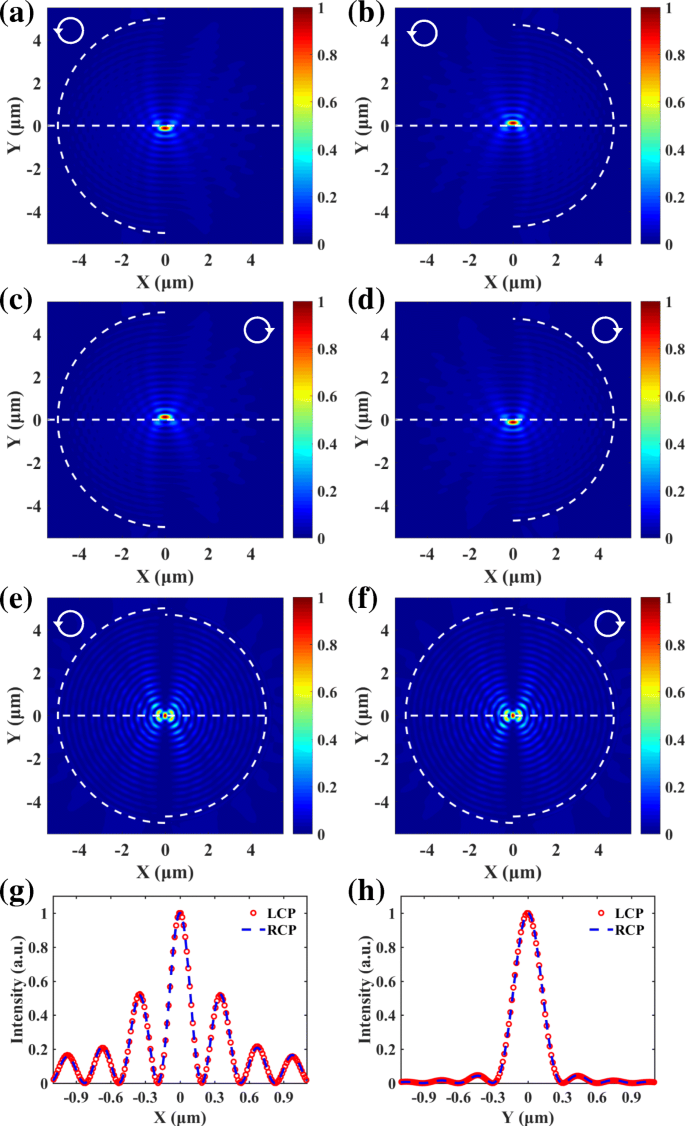
LCPライトの場合、左半円スリット（ a ）によって生成されたSPPフォーカス ）と右半円スリット（ b ）それぞれ下向きと上向きにシフトします。 RCPライトの場合 c および d 、SPPフォーカスの位置が逆になります。 e 、 f スピンに依存しないプラズモンレンズによって生成されたSPPフォーカスは、すべてLCPおよびRCP光の中心にあります。 g 、 h SPPフォーカスの横方向および縦方向の分布

図2eおよびfに示すように、LCPおよびRCPライトによって生成されたSPPフィールドはすべて中央に集中しています。入射光の波長は632.8nmであり、SPPの対応する波長λ _sp Au /空気インターフェースの場合は606nmです[12、36]。左右の半円形スリットの半径は5μmと4.697μmです。 SPPフォーカスの正規化された横方向および縦方向の分布が抽出され、図2gおよびhで比較されます。図2a〜dのSPPフォーカスのスピン依存の横方向シフトは消えます。 LCPとRCPの光によって生成されるSPPフォーカスの位置とプロファイルはまったく同じであり、スピンに依存しないプラズモンレンズの実現可能性を検証します。

全波数値シミュレーションも、有限差分時間領域（FDTD）法に基づいて実行されます。パラメータは、ホイヘンス-フレネル原理を使用した分析計算で使用されるものと同じに保たれます。図3aおよびbでシミュレートされたSPP分布は、分析結果と非常によく一致しています。図3cおよびdの横方向および縦方向の分布は、 x に沿った焦点の半値全幅（FWHM）を示しています。 -および y -方向（190nmおよび260nm）はすべて半波長よりも小さいです。 SPPフォーカスの位置、FWHM、および強度はすべて、入射光のスピン状態から独立しています。半円形のスリットによって励起されたSPPは、伝播中に徐々に減衰します。伝搬損失は金属の吸収によって引き起こされ[11、12]、複素誘電率（ε）を使用してシミュレーションで考慮されています。 _Au =− 11.821 + 1.426 i ）。したがって、伝播損失は、SPPのスピン依存の集束に影響を与えません。図3eとfは、焦点の周りの位相分布を示しています。緑の点線の矢印で示されているように、時計回りと反時計回りの方向を持つ2つのスパイラル位相は互いに釣り合いが取れており、スピンに依存しないSPPフォーカシングにつながります。中央のフラットフェーズはフォーカスエリアに対応します。図3eとfのSPPの位相分布は、励起光のスピン状態が異なると異なることに注意してください。ただし、これらは中心対称であるため、SPPの強度分布も中心対称である必要があります。中心対称性の要件を満たすには、LCPとRCPライトによって生成されるSPPフォーカスを両方とも中心に配置する必要があります。したがって、スピンに依存しない強度分布は、必ずしも位相分布がスピンに依存しないことを意味するわけではない。ここでは、主にスピン非依存と言うときの電界強度を指します。

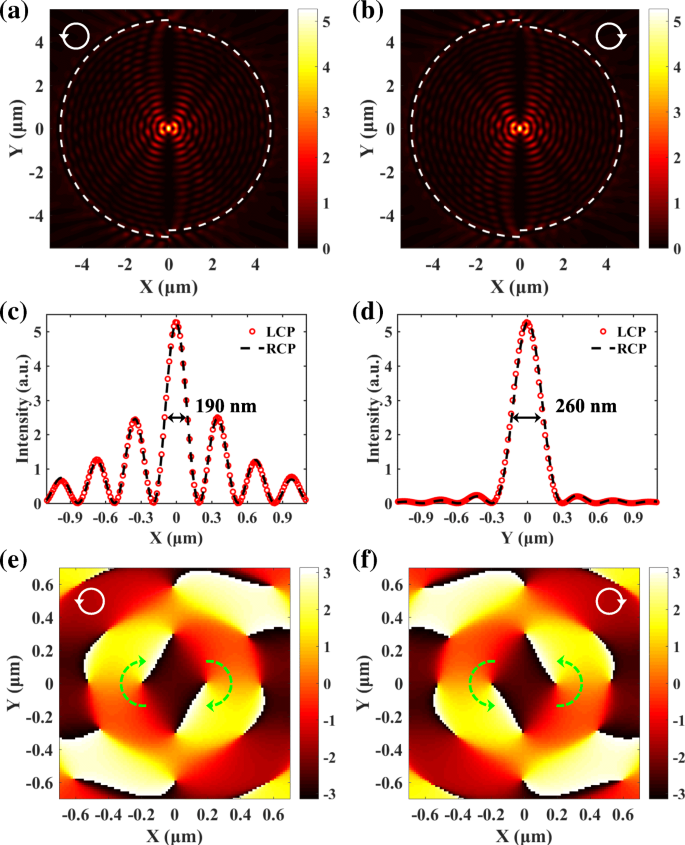
LCPによって生成されたシミュレートされたSPPフィールド（ a ）およびRCP（ b ） ライト。 c 、 d 対応する横方向および縦方向の分布。 LCPライトとRCPライトによって生成されるSPPフォーカスの位置とプロファイルはまったく同じです。 e 、 f 焦点の周りの対応する位相分布。 e の方向が反対の2つのスパイラルフェーズ および f スピンに依存しないSPPフォーカシングの起源である互いに打ち消し合うことができます

半径Δ r の違いによるSPP分布の変化 明らかにされます。半径がΔ r を満たす場合 =nλ _sp 、2つの半円形スリットは、スパイラル位相が0から2 πまで変化する1つの円形スリットに相当します。 。 Δ r を取る =λ _sp 例として、図4aおよびbに示すように、スピン依存のSPP渦を取得できます。図4aおよびbの挿入図の位相分布は、SPP渦のトポロジカル電荷が l であることを示しています。 =1および l =− 1（LCPライトとRCPライトの場合）。したがって、分離Δ r 2つの半円形スリットの間は、プラズモンレンズの性能に大きな影響を与えます。 2つのスパイラル相は互いに打ち消し合うことができ、スピンに依存しないSPPフォーカシングは、式（1）の場合にのみ達成できます。 （6）を満たしています。さらに、式によると。 （6）、スリットの半径と中心角は、プラズモンレンズの集束特性に影響を与えることができませんでした。中心角が2 πのアークスリットの場合 / 3、 r ₁ =3.7μmおよび r ₂ =2.2μm、\（\ Delta r =\ frac {5} {2} {\ lambda} _ {\ mathrm {sp}} \）、およびLCPおよびRCP光によって励起されたSPPはすべて、中央に集束されます。図4cおよびdに示されています。さらに、提案されたアプローチは、スパイラルスリットに適用することができます。 \（{r} _1 \ left（\ theta \ right）={r} _0 + \ frac {\ theta} {\ pi} {\ lambda} _ {\ mathrm {sp}} \）で記述されるスパイラルスリットの場合、 r で別のスパイラルスリットを追加する ₂ = r ₁ − λ _sp / 2は、スパイラル位相を相殺し、スピンに依存しないSPPフォーカシングを実現できます。図4eおよびfのSPP分布は、提案されたアプローチの多様性と堅牢性を示しています。

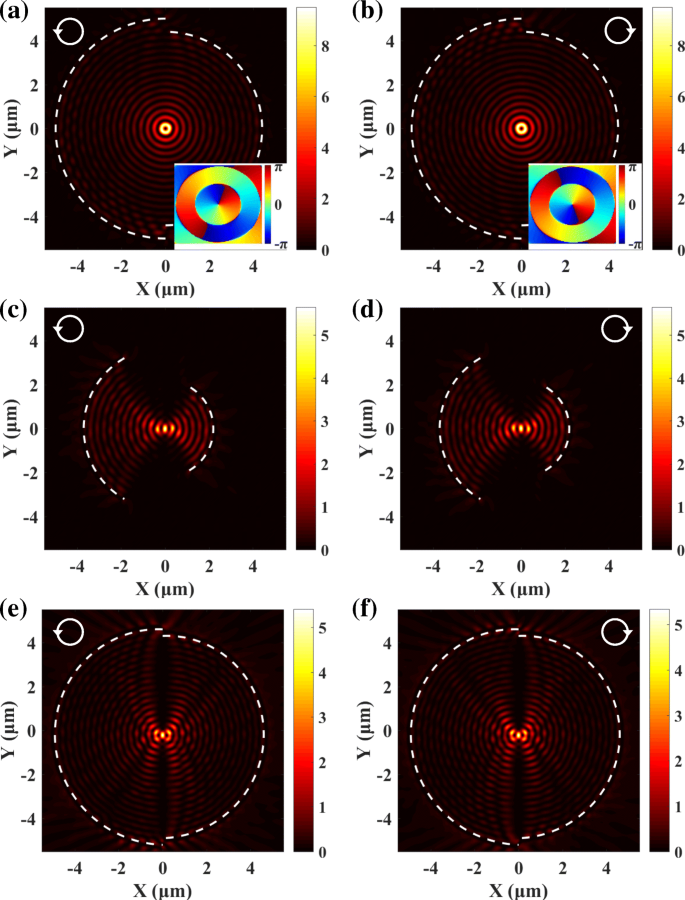
Δ r の半円形スリットの場合 =λ _sp 、LCPによって励起されたSPP渦（ a ）およびRCP（ b ）反対のトポロジー電荷を示します。半径と中心角の変更は、スピンに依存しないSPPの集束には影響しません（ c 、 d ）。提案されたアプローチは、スパイラルスリット（ e ）にも適しています。 、 f ）

Pancharatnam-Berryフェーズに基づくスピンに依存しないSPPフォーカシング

上記の議論では、半円形のスリット全体を扱ってきました。図5aに示すように、半円形のスリットはサブ波長の長方形のスリットに分割できます。このようにして、スリットの配向角度によって決定されるジオメトリPancharatnam-Berry（PB）位相が[37、38]に取り込まれ、φとして表すことができます。 _PB =σ _m α 。したがって、各サブ波長スリットによって生成されるSPPの位相は次のようになります。

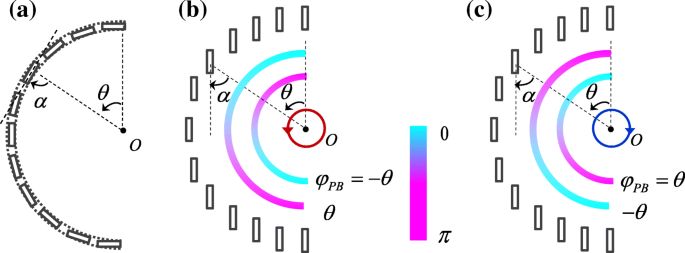
半円形のスリットは、サブ波長の長方形のスリットに分割できます（ a ）。スリットが垂直に配置されている場合、各スリットによって生成されたPB位相を利用して、LCPによって生成されたスパイラル位相を局所的にキャンセルすることができます（ b ）およびRCPライト（ c ）

スパイラル位相は、PB位相分布を操作することでローカルにキャンセルできます。図5aでは、PB位相は一定のφです。 _PB =π / 2であり、スパイラルフェーズには影響しません。 PB位相がφを満たす場合 _PB =σ _m θ 、スパイラル位相は局所的に平衡化され、各スリットによって生成されるSPPの位相はΦ _sp です。 （θ ）=0。したがって、サブ波長スリットは、図5bおよびcに示すように、垂直方向に沿って位置合わせする必要があります。

垂直サブ波長スリットで構成されるスピン非依存プラズモンレンズによって生成されたSPPの強度分布を図6aおよびbに示します。スリットの幅と長さはそれぞれ50nmと200nmです。図6cおよびdのSPPフォーカスの縦方向および横方向のプロファイルは、LCPおよびRCPライトによって生成されたSPPフォーカスの位置、FWHM、および強度が区別できないことを示しています。図3cおよびdのSPP分布と比較すると、焦点の横方向のFWHMはほぼ同じですが、縦方向のFWHMは3倍以上大きくなっています。これは、図3cとdの反対側の半円形スリットによって生成されたSPPが、SPPフォーカスの横方向のサイズを効果的に圧縮できるためです。図6eとfは、焦点の周りに均一な角度位相分布を示しており、スパイラル位相は観察されていません。これは、スパイラルフェーズがPBフェーズによってローカルにキャンセルされたためです。これは、図3eおよびfのスパイラル位相を保持する二重半円形スリットアプローチとは明らかに異なります。半径と中心角の変更は、SPPレンズの焦点特性に影響を与えません。図6gとhは、中心角が2 πのスリットによって生成されたスピンに依存しないSPP分布を示しています。 / 3および半径 r =2μm。

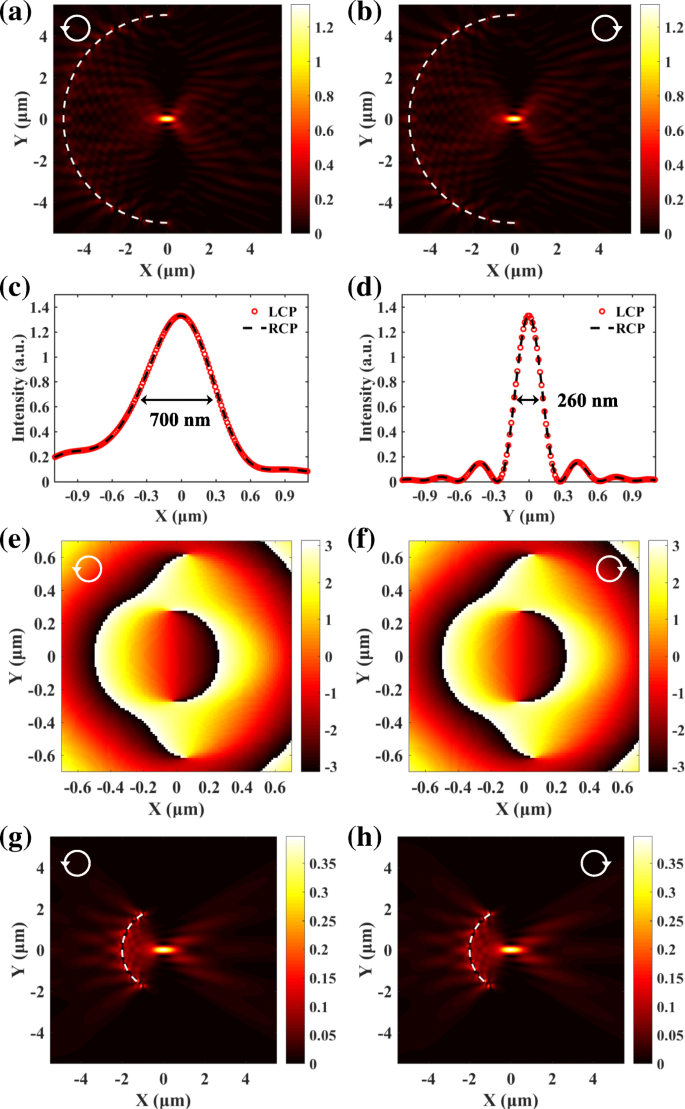
a 、 b レンズのスピンに依存しないSPPフォーカシングは、サブ波長スリットで構成されていました。 c 、 d SPPフォーカスの横方向および縦方向のプロファイル。 e 、 f 対応する位相分布。 g 、 h スピンに依存しないSPPフォーカシングは、半径と中心角の変化の影響を受けません

結論

結論として、別のスパイラルフェーズまたはPancharatnam-Berryフェーズを導入することにより、スピン依存スパイラルフェーズのバランスをとることが、スピン非依存SPPフォーカシングの基本原理です。 LCPおよびRCP光によって生成されるSPP焦点の位置とプロファイルは、スピンに依存しないプラズモンレンズとまったく同じです。この研究はさらに、スパイラル位相が半円形プラズモンレンズの集束特性を決定する決定的な要因であることを明らかにしています。さらに、提案された方法は、構造をスケーリングすることにより、他の周波数帯域で偏波に依存しないデバイスを設計するために利用できます[39、40]。

メソッド

3D数値シミュレーションは、商用ソフトウェアLumerical FDTDSolutionsを使用して実行されます。シミュレーションでは、幅240nmの半円形スリットが厚さ150nmの金膜にエッチングされ、基板はSiO ₂ です。 屈折率は1.46です。金膜の屈折率は、ジョンソンとクリスティのモデルから取得できます[36]。メッシュ精度は3に設定され、各メッシュセルの対応するサイズは約13×13×40 nmであり、精度、メモリ要件、およびシミュレーション時間の間で適切なトレードオフを実現できます。 x に8つのレイヤーがある完全一致レイヤー（PML） -、 y -、および z -方向は、伝播するSPPフィールドを吸収するための境界条件として使用されます。水平偏光と位相の異なる垂直偏光σ _± π / 2は、LCPおよびRCP光源を合成するために使用されます。また、励起されたSPPへの影響を避けるために、光源はサンプルを裏側から照らします。 SPPフォーカスのプロファイルを取得するには、2Dフィールドモニターを金膜の50 nm上に配置します。これは、SPPの減衰長の範囲内です。

略語

FDTD：

有限-異なる時間領域

FT：

フーリエ変換

FWHM：

最大幅の半分で全幅

LCPライト：

左円偏光

PBフェーズ：

Pancharatnam-ベリーフェーズ

RCPライト：

右円偏光

SHE：

スピンホール効果

SPP：

表面プラズモンポラリトン