ベン図をカルノー図のように見せること

円で始まる A 長方形の A ’ユニバース 下の図（a）では、ベン図をほぼカルノー図に変形しています。

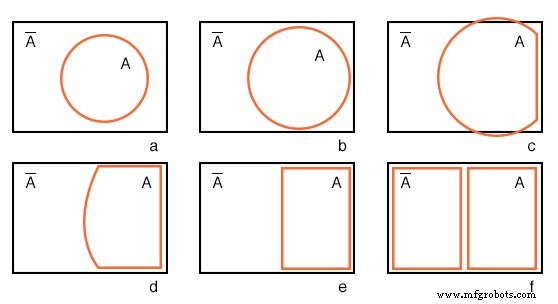
円を拡大します A （b）と（c）で、長方形の A ’ユニバースに準拠します。 （d）で、 A を変更します （e）の長方形に。 A の外に残っているもの は A ’ 。 A ’に長方形を割り当てます （f）で。また、カルノー図ではシェーディングを使用しません。これまでのところ、1変数のカルノー図に似ていますが、ほとんど役に立ちません。複数の変数が必要です。

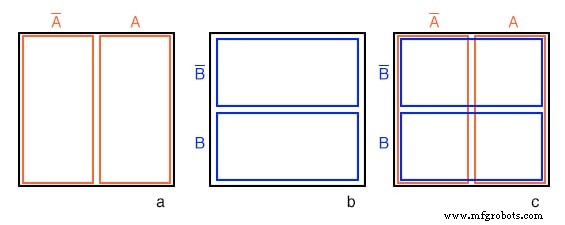
上の図（a）は、 A を示す前のベン図と同じです。 および A ’ ラベル A を除いて、上記 および A ’ それぞれの領域内ではなく、図の上にあります。 B の「正方形のベン図」を取得するために、図（a〜f）と同様のプロセスを実行したと想像してください。 および B ’ 真ん中の図（b）に示すように。

ここで、ベン図の場合と同じように、図（a）と（b）の図を重ね合わせて、（c）の結果を取得します。これを行う理由は、2つの重複する領域に共通する可能性があることを観察できるようにするためです。たとえば、 A オーバーラップ B 。図（c）の右下のセルは、 AB に対応します。 ここで A オーバーラップ B 。

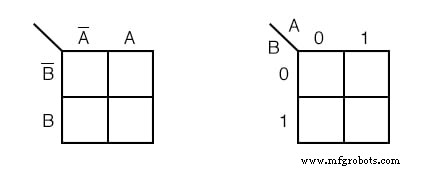
上記の（c）のようなカルノー図を描くのに時間を無駄にせず、代わりに上記のように簡略化したバージョンをスケッチします。 A ’の下の2つのセルの列 A ’に関連付けられていると理解されています 、および見出し A その下のセルの列に関連付けられています。 B ’が先頭にある行 右側のセルに関連付けられています。

同様の方法で B その右側のセルに関連付けられています。簡単にするために、ベン図のようにさまざまな領域を明確に描写していません。

右上のカルノー図は、ほとんどのテキストで使用されている代替形式です。変数の名前は対角線の横に表示されます。

A 対角線の上は、変数 A （および A ’ ）が列に割り当てられます。 0 A ’の代わりになります 、および 1 A の代わりに 。 B 対角線の下は行に関連付けられています： 0 B ’ 、および 1 B の場合

例：

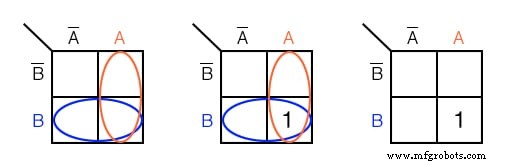
ブール式 AB に対応するセルをマークします 上記のカルノー図で 1

解決策：

A に対応する領域に陰影を付けるか丸で囲みます 。次に、 B に対応する領域をシェーディングまたは囲みます 。 2つの領域のオーバーラップは AB 。 1 を配置します このセルで。必ずしも A を同封する必要はありません および B 左上のような地域。

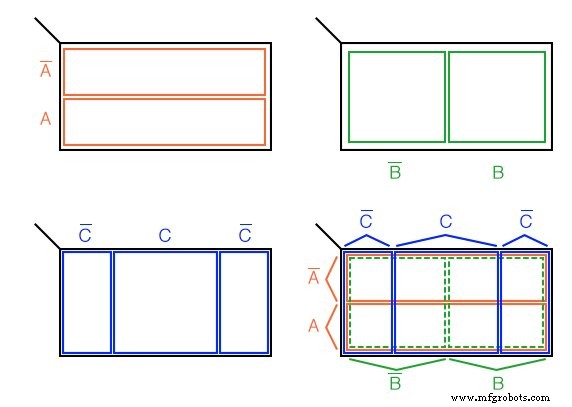
3変数Kマップ

地域のようなベン図から始めて、上記の3変数カルノー図を作成します。宇宙（黒い長方形の内側）は、 A 'の2つの狭い狭い長方形の領域に分割されます および A 。変数 B ’ および B 宇宙を2つの正方形の領域に分割します。 C 長方形の中央にある正方形の領域を占め、 C ’ C の両側で2つの垂直の長方形に分割します 正方形。

最後の図では、3つの変数すべてを重ね合わせて、さまざまな領域に明確にラベルを付けようとしています。領域は、カラー印刷なしではあまり目立たず、他の3つの図と比較するとより目立ちます。

この3変数 K-Map （カルノー図）には2 ³ があります =8 セル 、マップ内の小さな正方形。個々のセルは、3つのブール変数（ A、B、C ）によって一意に識別されます。 ）。たとえば、 ABC ’ 右下のセル（*）、 A’B’C ’を一意に選択します 左上のセル（x）を選択します。

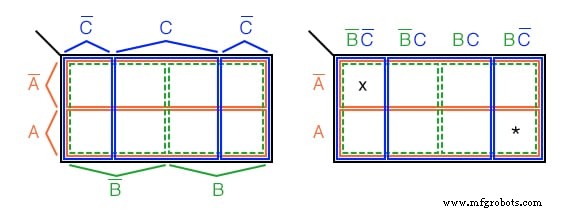
通常、左上に示すようにカルノー図にラベルを付けることはありません。この図は、4セル領域の単一のブール変数によるマップカバレッジを明確に示しています。

カルノー図には、右の図のようにラベルが付けられています。各セルは、3変数の製品用語によって一意に識別されます。 、ブール値の AND 表現。たとえば、 ABC ’ A に続く 右に横に並んで BC ’ 列を下に、両方とも右下のセルで交差します ABC ’ 。上の図（*）を参照してください。

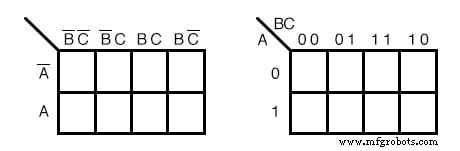
上記の2つの異なる形式の3変数カルノー図は同等であり、最終的な形式になります。右側のバージョンは、ブールアルファベットのヘッダーと補完バーを1と0だけで書き留める必要がないため、少し使いやすくなっています。右側のマップの形式を使用して、一部のテキストで左側のマップを探してください。 。左側の列ヘッダー B’C ’、B’C、BC、BC’ 00、01、11、10 と同等です 右側に。行ヘッダー A、A ’ 0、1 と同等です 右の地図にあります。