有限状態機械
これまで、提示されたすべての回路は組み合わせでした 回路。つまり、その出力は現在の入力のみに依存します。そのタイプの回路の以前の入力は、出力に影響を与えません。
ただし、回路に「メモリ」が必要なアプリケーションはたくさんあります。以前の入力を記憶し、それらに従って出力を計算します。出力が現在の入力だけでなく入力の履歴にも依存する回路は、シーケンシャル回路と呼ばれます。 。
このセクションでは、このような順序回路を設計および構築する方法を学習します。この手順がどのように機能するかを確認するために、例を使用して、トピックを学習します。
それで、時計で動作し、手動ボタンから入力を読み取るデジタルクイズゲームがあるとしましょう。ただし、スイッチが回路に送信するHIGHパルスは1つだけにする必要があります。ボタンをゲーム回路に直接引っ掛けると、指が達成できる数クロックサイクルの間、HIGHが送信されます。一般的なクロック周波数では、指が十分に速くなることはありません。
設計手順には、作業を完了するために従う必要のある特定の手順があります。
ステップ1
設計手順の最初のステップは、回路に何をさせたいかをシンプルで明確な言葉で定義することです。
「私たちの使命は、手動ボタンを押したときに1サイクルだけのHIGHパルスを送信し、ボタンを押してもう一度押すまで別のパルスを送信しない二次回路を設計することです。」
ステップ2
次のステップは、状態図を設計することです。
これは、円と矢印で作成された図であり、回路の動作を視覚的に説明しています。数学的には、順序回路の動作を説明するこの図は有限状態マシンです。これはムーア有限状態マシンであることに注意してください。
その出力は、入力ではなく、現在の状態のみの関数です。これは、入力が出力に影響を与えるMealy Finite StateMachineとは対照的です。このチュートリアルでは、ムーア有限状態マシンのみを調べます。
回路の状態図は次のとおりです:(下の図)
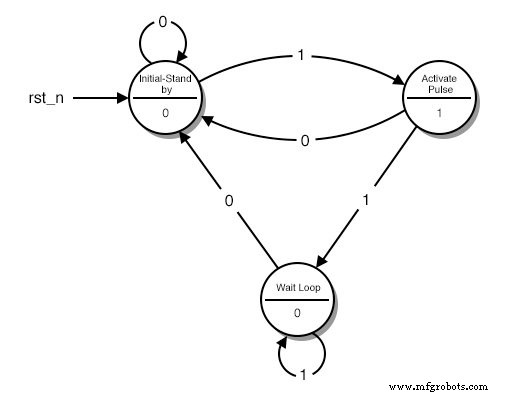
状態図
すべての円は「状態」を表します。これは、マシンを見つけることができる明確に定義された状態です。円の上半分に、その状態を示します。説明は、その状態で回路が何をすることになっているのかを思い出すのに役立ちます。
- 最初の円は「スタンバイ」状態です。これが私たちの回路が始まり、別のボタンが押されるのを待つ場所です。
- 2番目の円は、ボタンが押されたばかりで、回路がHIGHパルスを送信する必要がある状態です。
- 3番目の円は、ボタンが「スタンバイ」状態に戻る前に、ボタンが離されるのを回路が待機している状態です。
円の下部には、回路の出力があります。回路が特定の状態でHIGHを送信するようにしたい場合は、その状態に1を設定します。それ以外の場合は0を入力します。
すべての矢印は、ある状態から別の状態への「遷移」を表しています。遷移は、クロックサイクルごとに1回発生します。現在の入力に応じて、毎回異なる状態になる場合があります。すべての矢印の中央にある数字に注意してください。これが現在の入力です。
たとえば、「初期スタンバイ」状態にあり、1を「読み取る」場合、図は「パルスのアクティブ化」状態に移行する必要があることを示しています。 0を読み取る場合は、「初期スタンバイ」状態を維持する必要があります。
それで、私たちの「機械」は正確に何をしますか? 「初期-スタンバイ」状態から開始し、入力で1が読み取られるまで待機します。次に、「パルスのアクティブ化」状態になり、出力でHIGHパルスを送信します。ボタンを押し続けると、回路は3番目の状態である「待機ループ」になります。
そこで、出力でLOWを送信している間、ボタンが離される(入力が0になる)まで待機します。その後、もう一度やり直します!
これは、簡単な手順では説明できないため、設計手順の中でおそらく最も難しい部分です。状態図を設定するには、経験と少し鋭い思考が必要ですが、残りは事前に決定された一連の手順にすぎません。
ステップ3
次に、図のさまざまな状態を説明する単語をバイナリに置き換えます。 数字。初期状態で割り当てられた0から列挙を開始します。次に、すべての州に番号が付けられるまで、好きな州で列挙を続けます。結果は次のようになります:(下の図)
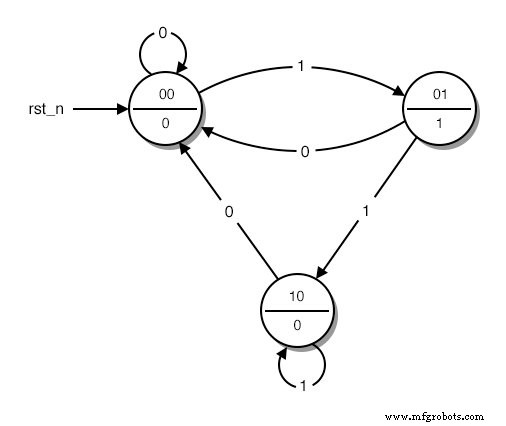
コード化された状態の状態図
ステップ4
その後、状態テーブルに入力します 。このテーブルには非常に特殊な形式があります。例の表を示し、それを使用して記入方法を説明します。(下の図)
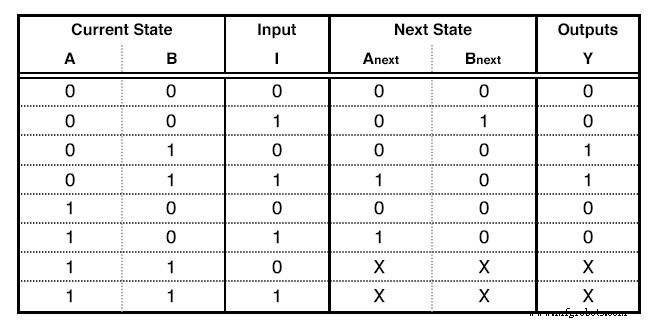
状態テーブル
最初の列は、状態図に割り当てた最大数のビットと同じ数です。 5つの状態がある場合、100まで使用します。つまり、3つの列を使用します。この例では、10まで使用したため、必要な列は2つだけです。これらの列は、現在の状態について説明しています。 私たちの回路の。
[現在の状態]列の右側に、入力列と記述します。 。これらは、入力変数と同じ数になります。この例には入力が1つだけあります。
次に、次の状態の列を記述します 。これらは、現在の状態の列と同じ数です。
最後に、出力列を記述します。 。これらは私たちの出力と同じ数です。この例には、出力が1つだけあります。 More Finite State Machineを構築したため、出力は現在の入力状態のみに依存します。これが、出力列に2つの1がある理由です。これにより、入力Iに依存しない出力ブール関数が生成されます。詳細については、読み続けてください。 [現在の状態]列と[入力]列は、テーブルの入力です。 0から次までのすべての2進数を入力します:
2 (現在の状態の列の数+入力列の数) -1
幸いなことに聞こえるよりも簡単です。通常、状態図で作成した実際の状態よりも多くの行がありますが、それで問題ありません。
[次の状態]列の各行には、次のように入力します。状態図で、同じ行の現在の状態から同じ行の入力をたどったときに到達する状態を入力します。現在の状態番号が状態図の実際の状態に対応していない行を入力する必要がある場合は、ドントケア用語(X)を入力します。結局のところ、私たちは存在しない州からどこに行くことができるかを気にしません。そもそもそこにはいないでしょう!繰り返しになりますが、思ったよりも簡単です。
出力列には、状態図の対応する現在の状態の出力が表示されます。
状態テーブルが完成しました。状態図と同じくらい完全に回路の動作を説明します。
ステップ5a
次のステップは、その理論上の「機械」を取り、それを回路に実装することです。ほとんどの場合、この実装にはビーチサンダルが含まれます。このガイドは、この種の実装に特化しており、D-フリップフロップとJK-フリップフロップの両方の手順について説明します。 T-フリップフロップは、前の2つのケースと類似しているため、含まれません。使用するフリップフロップの選択は任意であり、通常はコスト要因によって決定されます。最良の選択は、分析を実行し、どのタイプのフリップフロップが最小数の論理ゲートとより少ないコストをもたらすかを決定することです。
まず、D-フリップフロップを使用して「マシン」を実装する方法を検討します。
状態列と同じ数のD-フリップフロップが必要になります。この例では2です。フリップフロップごとに、状態テーブル(下の図)にフリップフロップの入力の名前(この場合は「D」)を含む列をもう1つ追加します。各フリップフロップに対応する列には、現在の状態から次の状態に移行するためにフリップフロップに入力する必要がある入力が記載されています。 。 D-フリップフロップの場合、これは簡単です。必要な入力は次の状態と同じです。 Xを含む行では、この列にもXを入力します。
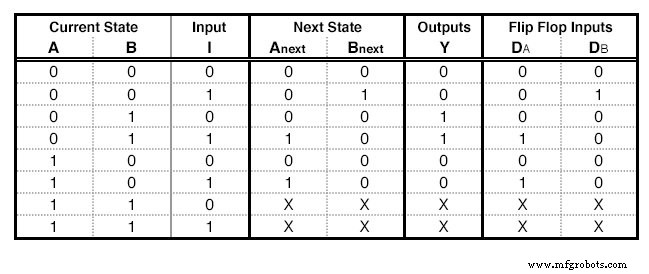
Dの状態テーブル-フリップフロップの励起
ステップ5b
JK-フリップフロップでも同じ手順を実行できます。ただし、いくつかの違いがあります。 JK-フリップフロップには2つの入力があるため、フリップフロップごとに2つの列を追加する必要があります。各セルの内容は、JKの励起表によって決定されます:

この表は、状態Qから状態Qに移動する場合 next 、各端子に固有の入力を使用する必要があります。たとえば、0から1に移行するには、Jに1を与える必要があり、気にしない どの入力をターミナルKに送りますか。
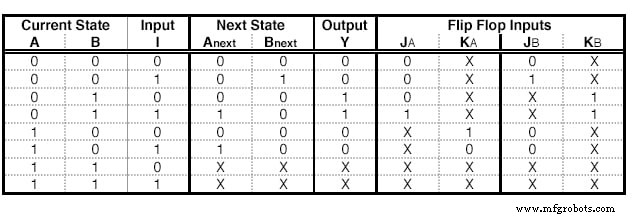
JKを使用した状態テーブル-フリップフロップの励起
ステップ6
私たちは手続きの最終段階にあります。残っているのは、フリップフロップの入力と出力を生成するブール関数を決定することです。フリップフロップ入力ごとに1つのブール関数を抽出します。これは、カルノー図を使用して実行できます。このマップの入力変数は、現在の状態変数およびです。 入力。
とはいえ、D-フリップフロップの入力関数は次のとおりです:(下の図)
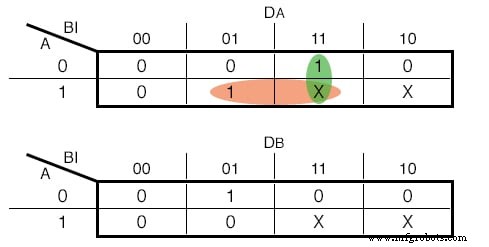
Dのカルノー図-フリップフロップ入力
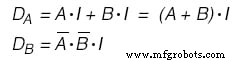
JK-フリップフロップを使用することを選択した場合、関数は次のようになります:(下の図)
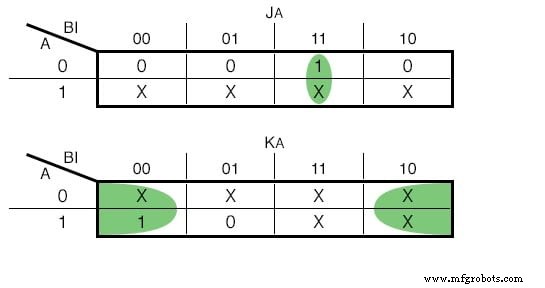
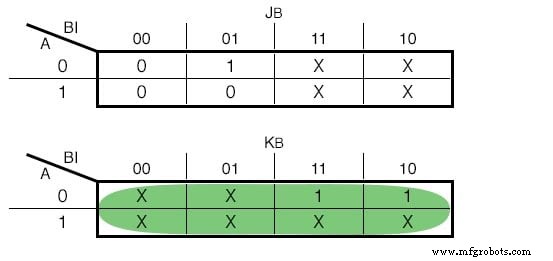
JKのカルノー図-フリップフロップ入力
カルノー図は、出力の機能も決定するために使用されます:(下の図)
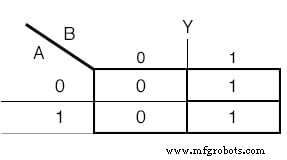
出力変数Yのカルノー図
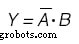
ステップ7
回路を設計します。フリップフロップを配置し、論理ゲートを使用して、計算したブール関数を形成します。ゲートは、フリップフロップの出力と回路の入力から入力を受け取ります。時計をフリップフロップに接続することを忘れないでください!
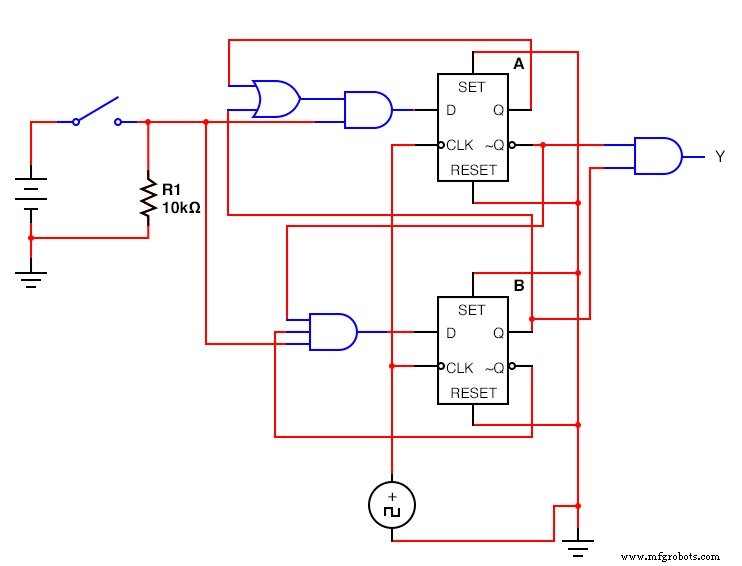
D-フリップフロップバージョン:(下の図)

完成したD-フリップフロップシーケンシャル回路
JK-フリップフロップバージョン:(下の図)
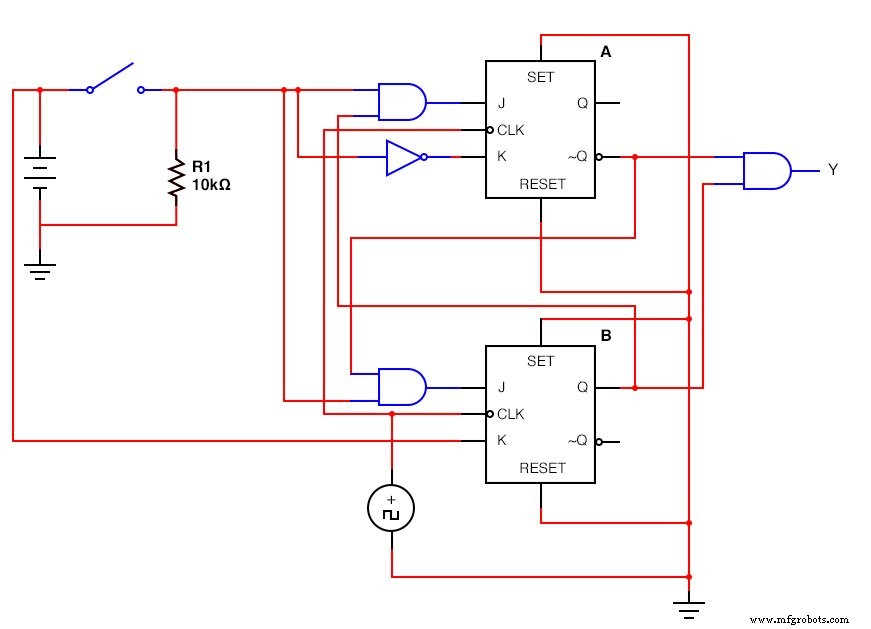
完成したJK-フリップフロップシーケンシャル回路
これです!シーケンシャル回路の設計と構築に成功しました。最初は大変な作業に思えるかもしれませんが、練習と繰り返しの後、手順は簡単になります。シーケンシャル回路は、より大きな回路の制御部分として便利であり、考えられるあらゆるシーケンシャルロジックタスクを実行できます。空が限界! (または少なくとも回路基板)
レビュー:
- シーケンシャルロジック関数には「メモリ」機能があり、出力を決定するために過去の入力を考慮に入れます。
- 有限状態マシンは、シーケンシャル論理関数の抽象的な数学モデルです。有限の入力、出力、および状態の数があります。
- FSMは、フリップフロップを使用して実際の回路に実装されます
- 実装手順を実行するには、特定の手順(アルゴリズム)が必要です。
産業技術



