分流の法則（CDR）–ACおよびDC回路の解決例

抵抗性、誘導性、容量性回路の現在の分割「CDR」

何 現在の分流の法則（CDR）ですか？

多数の要素が並列に接続されている場合、電流はいくつかの並列パスに分割されます。そして、電圧はソース電圧に等しいすべての要素で同じです。

つまり、電流が複数の並列パスを通過する場合（分圧器の規則「VDR」または分圧器を使用して直列回路の電圧を計算します）、各パスの電流分割。特定の分岐を通過する電流の値は、その分岐のインピーダンスによって異なります。

現在の分流の法則または現在の分流の法則は、回路を解くために広く使用されている最も重要な式です。各分岐のインピーダンスと合計電流がわかれば、各分岐を流れる電流を見つけることができます。

電流は常に最小のインピーダンスを流れます。したがって、電流はインピーダンスと反比例の関係にあります。オームの法則によれば、ノードに入る電流はインピーダンスに反比例してノード間で分割されます。

これは、電流が最小の抵抗パスを選択したため、インピーダンスの値が小さいほど電流が大きくなることを意味します。また、抵抗値が大きいほど電流が最小になります。

回路要素​​によると、電流分流の法則は、抵抗、インダクタ、およびコンデンサを表す場合があります。

抵抗回路の現在の分流の法則

抵抗性分流の法則を理解するために、抵抗が並列に接続されている回路を考えてみましょう。回路図を下図に示します。

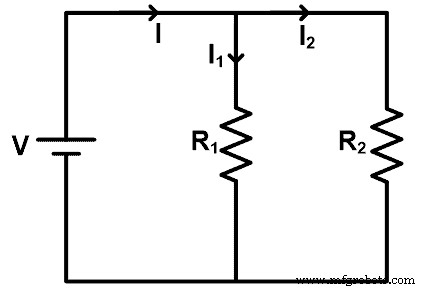
この例では、すべての抵抗にDC電源を供給します。抵抗器の電圧はソース電圧と同じです。しかし、並列接続のため、電流は異なるパスに分割されます。電流は各ノードで分割され、電流の値は抵抗に依存します。

分流の法則を使用して、各抵抗を通過する電流の値を直接見つけることができます。

この例では、ソースから供給される主電流はIです。これは、2つの抵抗R ₁に分割されます。 およびR₂ 。電流は抵抗R₁を通過します I ₁です 電流は抵抗R₂を通過します I ₂です 。

抵抗が並列に接続されているため。したがって、等価抵抗はR _eqです。 。

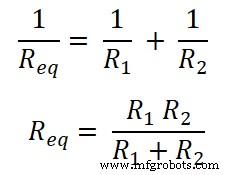
オームの法則に従って、

V =I R _eq

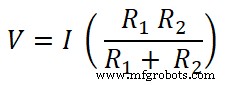
両方の抵抗がDC電源と並列に接続されています。したがって、抵抗の両端の電圧はソース電圧と同じです。そして、抵抗器R ₁を流れる電流 I ₁です 。

つまり、レジスタR ₁の場合;

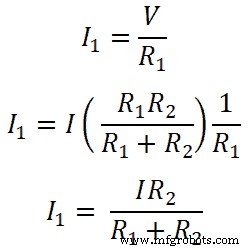
同様に、レジスタR ₂の場合;

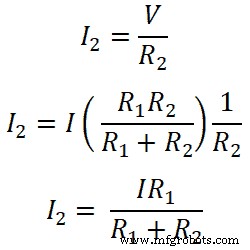
したがって、これらの式は、並列に接続された抵抗の分流の法則を示しています。これらの式から、抵抗器を通過する電流は、総電流と反対の抵抗を総抵抗で乗算した比率に等しいと言えます。

関連記事：

• テブナンの定理。解決例を含むステップバイステップガイド
• ノートンの定理。解決例を含むステップバイステップガイド

誘導回路の現在の分流の法則

インダクタが並列に接続されている場合、分流の法則を適用して、各インダクタを通過する電流を見つけることができます。分流の法則を理解するために、次の図に示すように、インダクタが並列に接続されている回路を使用します。

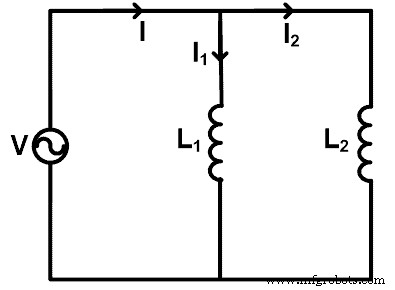
ここでは、2つのインダクター（L ₁ およびL₂ ）は電源電圧Vと並列に接続されています。電源を流れる合計電流は1アンペアです。電流はインダクタL₁を通過します I ₁です 電流はインダクタL₂を通過します I ₂です 。

次に、現在のI ₁の方程式を見つける必要があります。 およびI₂ 。そのために、等価インダクタンスL _eqを見つけます。;

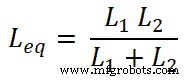
回路を流れる合計電流はIであり、次のように等しいことがわかっています;

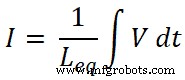
つまり、

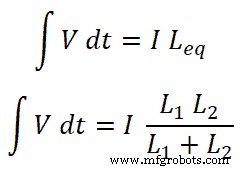
ここで、インダクタL ₁の場合 、このインダクタを流れる電流はI ₁ ;

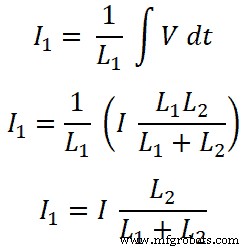
インダクタL ₂の場合;

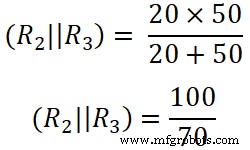
インダクタの電流分流の法則は、抵抗の分流の法則と同じです。

容量性回路の現在の分流の法則

コンデンサが並列に接続されている場合、分流の法則を使用して、各コンデンサを流れる電流を見つけることができます。コンデンサの分流の法則を理解するために、下の図に示すように、コンデンサが並列に接続されている例を取り上げます。

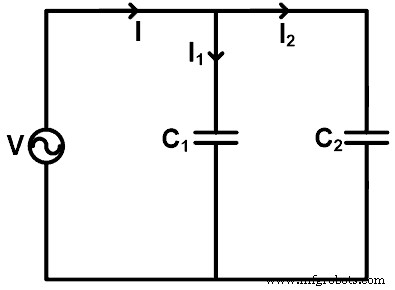
ここでは、2つのコンデンサ（C ₁ およびC₂ ）は電圧源Vと並列に接続されています。電流はコンデンサC ₁を通過します。 I _1、です 電流はコンデンサC₂を通過します I ₂です 。ソースを介して供給される合計電流はIです。

次に、現在のI ₁の方程式を見つける必要があります。 およびI₂ 。そのために、等価静電容量C _eqを見つけます。;

C _eq =C ₁ + C ₂

コンデンサを流れる電流の式はわかっています。そして、ソースによって供給される総電流の式は次のとおりです。

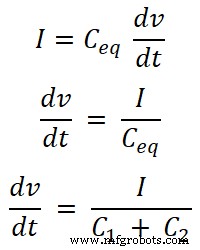
コンデンサC ₁の場合 、このコンデンサを流れる電流はI ₁ ;

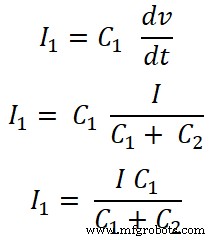
コンデンサC ₂の場合;

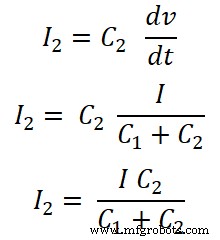
コンデンサの分流の法則は、インダクタと抵抗の分流の法則とは少し異なります。

コンデンサの分流の法則では、コンデンサを通過する電流は、総電流にそのコンデンサを掛けたものと総静電容量の比率です。

CDRを使用したACおよびDC回路の解決例

DC回路の現在のダイバールール

例：1

特定のネットワークの分流の法則により、各抵抗器を通過する電流を見つけます。

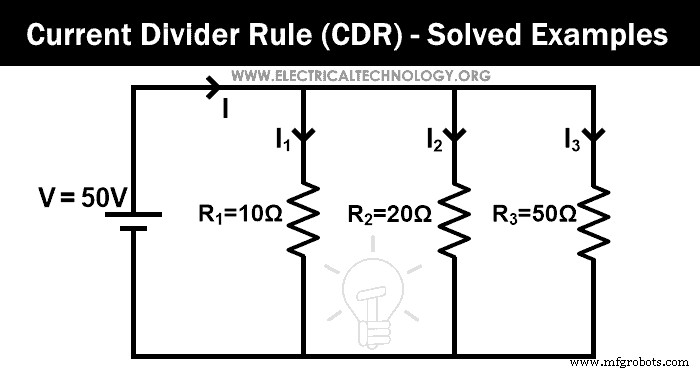
この例では、3つの抵抗が並列に接続されています。まず、等価抵抗を見つけます。

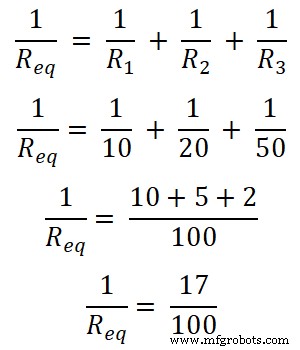
R _eq = 100/17

R _eq = 5.882Ω

ソースから供給される合計電流はIです。したがって、オームの法則によれば;

V =I R _eq

50V = I （5.882Ω）

I = 50V/5.882Ω

I = 8.5 A

ここで、電流分流の法則を最初の抵抗（10Ω）に適用し、この抵抗を流れる電流はI ₁です。;

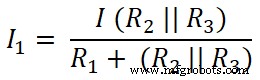
ここでR ₂ およびR₃ 並列に接続されています。したがって、R ₂間の等価抵抗を見つける必要があります。 およびR₃ 。

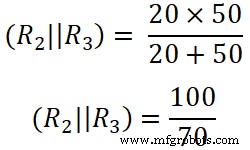
（ R ₂ || R ₃ ）=14.285Ω

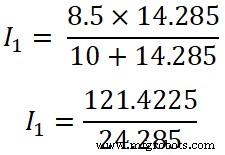
私 ₁ =4.9999≈5A

同様に、分流の法則を2番目の抵抗（20Ω）に適用し、この抵抗を通過する電流はI ₂です。;

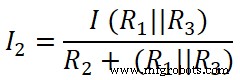
ここ、

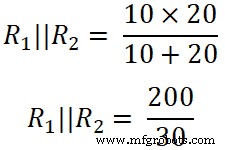
（ R ₁ || R ₃ ）=8.33Ω

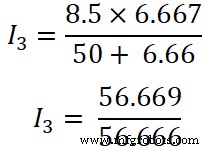
私 ₂ =2.499≈2.5A

ここで、分流の法則を3番目の抵抗（50Ω）に適用します。この抵抗を通過する電流はI ₃です。 。

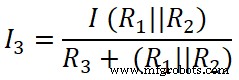
ここ、

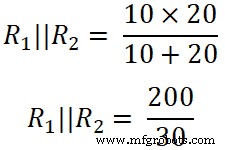
（ R ₁ || R ₂ ）=6.66Ω

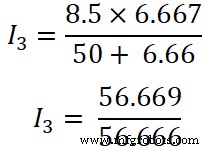
私 ₃ =1.00 A

したがって、3つの電流すべての合計は次のようになります;

私 ₁ +私 ₂ +私 ₃ =5 + 2.5 + 1 =8.5 A

そして、この電流は、ソースから供給される合計電流と同じです。

AC回路の現在のダイバールール

例-2

次の図に示すように、抵抗とコンデンサが並列に接続されたAC回路を考えてみます。分流の法則を使用して、抵抗とコンデンサを流れる電流を見つけます。 60Hzの周波数を考慮してください。

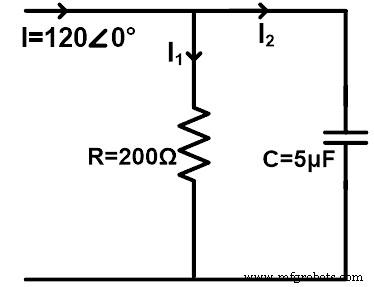
Z _R =200Ω=200∠0°Ω

Z _C =1 /（2π f C）=1 /（2π60（5×10 ⁶ ））

Z _C =10 ⁶ /（600π）

Z _C =530.78∠-90°Ω

これで、分流の法則に従って、電流の方程式は抵抗を通過します;

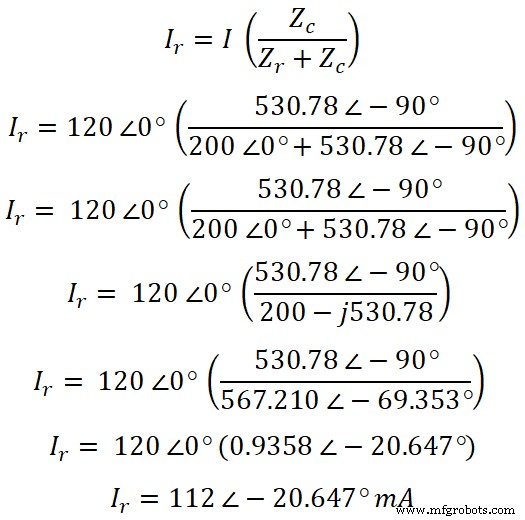
これで、同様に、電流がコンデンサを通過することがわかります。分流の法則によれば、コンデンサを流れる電流の式は次のとおりです。

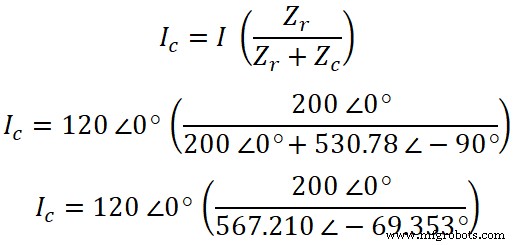
I _C =120∠0°（0.3526∠69.353°）

I _C =42.31∠69.353°

この答えを証明したい場合は、両方の電流を追加できます。そして、この電流の値はソース電流と同じです。

関連する電気回路解析チュートリアル：

• 補償定理–証明、説明、および解決された例
• 置換定理–解決された例を使用したステップバイステップガイド
• SUPERNODE回路解析–解決例を使用したステップバイステップ
• SUPERMESH回路解析–解決例を使用したステップバイステップ
• キルヒホッフの電流および電圧法（KCLおよびKVL）|解決した例
• クラメルの公式計算機–電気回路用の2および3方程式システム
ホイートストンブリッジ–回路、動作、派生、およびアプリケーション
• 電気電子工学計算機
• 5000以上の電気電子工学の公式と方程式