より大きな4変数カルノー図

グレイコードを生成する方法を知っていると、より大きなマップを作成できるはずです。実際に必要なのは、3変数マップの上部にある左から右のシーケンスを見て、4変数マップの左側にコピーすることだけです。以下を参照してください。

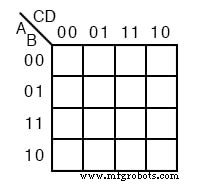
4つの変数Kマップの縮小

次の4つの変数カルノー図は、ブール代数には面倒なブール式の削減を示しています。ブール代数を使用して削減を行うことができます。

ただし、特に実行するロジックの削減が多い場合は、カルノー図の方が高速で簡単です。

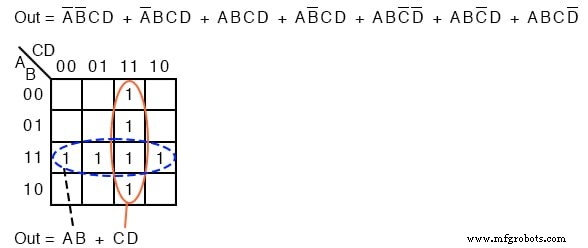
上記のブール式には7つの積項があります。これらは、上のKマップで上から下および左から右にマップされます。たとえば、最初のPターム A’B’CD マップの場所 A =0、B =0、C =1、D =1 に対応する、最初の行、3番目のセルです。 。

他の製品用語も同様に配置されます。可能な限り最大のグループを囲んで、4つのグループを2つ上に示します。

水平の破線のグループは、簡略化された製品用語 AB に対応します。 。垂直グループはブールCDに対応します。 2つのグループがあるため、 Out =AB + CD のSum-Of-Productsの結果には2つの製品用語が含まれます。 。

下の地図の隅をナプキンのように折りたたんで、4つのセルを物理的に隣接させます。

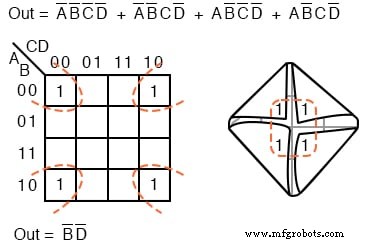
上記の4つのセルは、すべてブール変数 B ’を持っているため、4つのグループです。 および D ’ 共通して。つまり、 B =0 4つのセルの場合、 D =0 4つのセルの場合。

その他の変数（A、C） 0 です 場合によっては、 1 その他の場合、四隅のセルに関して。

したがって、これらの変数は（A、C） この4人のグループには関与していません。この単一のグループは、簡略化された結果の1つの製品用語としてマップから出てきます： Out =B’D ’

以下のKマップの場合、上端と下端を円柱に丸めて、8つの隣接するセルを形成します。

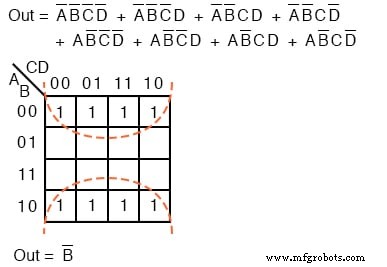
上記の8つのグループには、共通のブール変数が1つあります： B =0 。したがって、8つのグループの1つは、1つのp-termでカバーされます： B ’ 。元の8項のブール式は、 Out =B ’に簡略化されます。

4つの変数KマップのP項

以下のブール式には9つのp項があり、そのうち3つには4つではなく3つのブールがあります。違いは、4つのブール変数積項が1つのセルをカバーするのに対し、3つのブールp項はそれぞれセルのペアをカバーすることです。

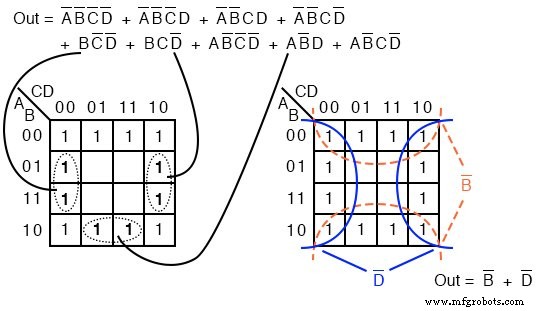
4つのブール変数の6つの積項は、上記の通常の方法で単一のセルとしてマップされます。 3つのブール変数項（それぞれ3つ）は、上記のセルペアとしてマップされます。

この時点では、p-termをK-mapにマッピングしており、引き出していないことに注意してください。

簡単にするために、8つのグループを2つ作成します。隅のセルは両方のグループで共有されます。これで結構です。実際、これは、セルを共有せずに8つのグループと4つのグループを形成するよりも優れたソリューションにつながります。最終的な解決策は Out =B ’+ D’

以下では、単純化されていないブール式をカルノー図にマップします。

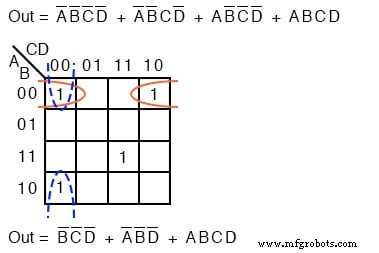
上記では、3つのセルが2つのセルのグループになっています。 4番目のセルは、「現実世界」の問題でよく発生するものと組み合わせることはできません。この場合、ブールp-term ABCD 簡略化プロセスでは変更されません。結果： Out =B’C’D ’+ A’B’D’ + ABCD

多くの場合、単純化の問題には複数の最小コストの解決策があります。以下に示すケースです。

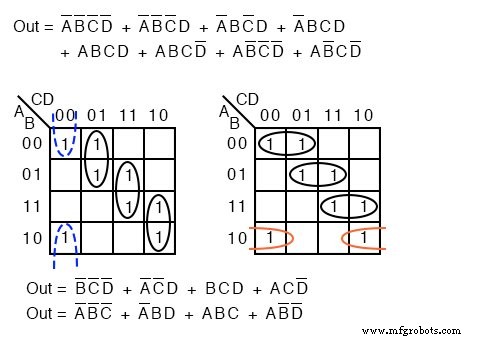
上記の両方の結果には、それぞれ3つのブール変数の4つの積項があります。どちらも同等に有効です最小コスト ソリューション。最終的な解決策の違いは、上記のようにセルがどのようにグループ化されているかによるものです。

最小コストのソリューションは、最小数の入力と最小数のゲートを備えた有効な論理設計です。

以下では、単純化されていないブール方程式を通常どおりにマップし、最初の単純化ステップとして4つのグループを形成します。残りの細胞を拾う方法がはっきりしないかもしれません。

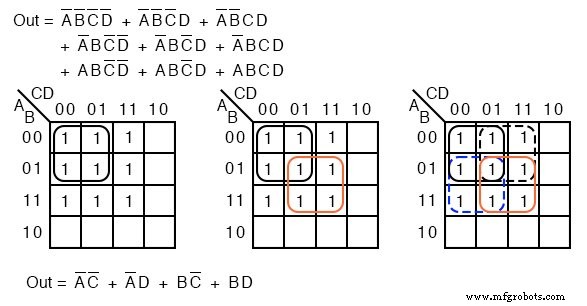
上の中央にある4つのグループでさらに3つのセルをピックアップします。まだ2つのセルが残っています。それらをピックアップするための最小コストの方法は、右上のように4つのグループとして隣接するセルとそれらをグループ化することです。

注意点として、3つのグループを形成しようとしないでください。グループ化は2の累乗、つまり1、2、4、8 ...

である必要があります。

以下に、2つの可能な最小コストソリューションの別の例を示します。セルをマッピングした後、4つのグループをいくつか形成することから始めます。

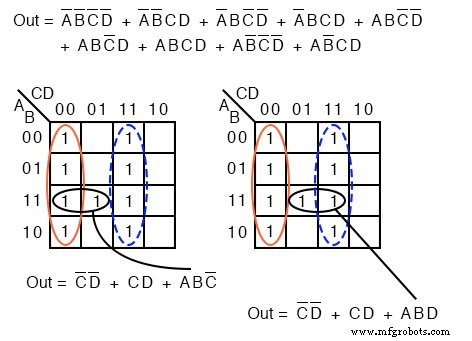
2つの解決策は、残りの1つのセルが2つのセルのグループとして4つの最初のグループと2番目のグループのどちらでグループ化されているかによって異なります。そのセルは、 ABC ’のいずれかとして出力されます。 または ABD 、あなたの選択。

いずれにせよ、このセルはいずれかのブール積項でカバーされます。最終結果は上に示されています。

以下に、左側のカルノー図または右側のブール代数を使用した簡略化の例を示します。プロット C ’ アドレス C =0 でカバーされるすべてのセルの領域としてマップ上に 、マップの左側にある8セル。次に、単一の ABCD をプロットします セル。

示されているように、その単一のセルは2セルのグループを形成します。これは、Pターム ABD に単純化されます。 、 Out =C ’+ ABD の最終結果 。

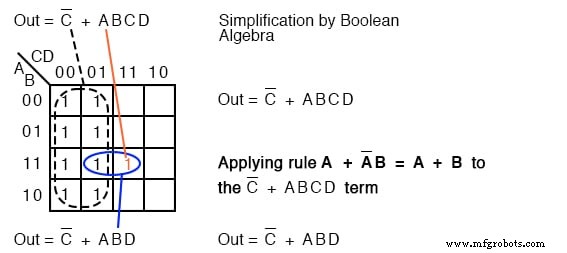
これ（上記）は、定理を覚えていると仮定すると、多くの作業を行わなくてもブール代数で減らすことができる4変数問題のまれな例です。

関連するワークシート：

• カルノーマッピングワークシート