MintermとMaxtermのソリューション

これまで、論理削減の問題に対するSum-Of-Product（SOP）ソリューションを見つけてきました。これらのSOPソリューションのそれぞれについて、Product-Of-Sumsソリューション（POS）もあります。これは、アプリケーションによっては、より便利な場合があります。

Product-Of-Sumsソリューションを使用する前に、いくつかの新しい用語を導入する必要があります。製品用語をマッピングするための以下の手順は、この章にとって目新しいものではありません。

maxtermsの新しい手順と比較するために、mintermsの正式な手順を確立したいだけです。

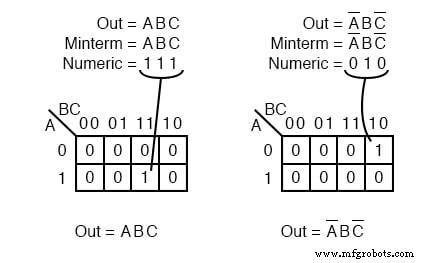
ミンターム

minterm 1 になるブール式です。 単一セルの出力の場合、および 0 ■カルノー図または真理値表の他のすべてのセル。 mintermに単一の 1 がある場合 残りのセルは 0 s、 1 の最小領域をカバーしているように見えます s。

左上の図は、minterm ABC を示しています 、単一の製品用語、単一の 1 それ以外の場合は 0 であるマップ内 s。 0 は表示していません s特に必要でない限り、それらを省略するのが通例であるため、この時点までのカルノー図にあります。もう1つの最小期間 A’BC ’ 右上に表示されます。

確認すべき点は、セルのアドレスがマップされているmintermに直接対応していることです。つまり、セル 111 minterm ABC に対応します 左上。

右上に、minterm A’BC ’が表示されます セル 010 に直接対応します 。ブール式またはマップには、複数のmintermが含まれる場合があります。

上の図を参照して、Kマップにmintermを配置する手順を要約してみましょう。

• マッピングするminterm（製品用語）用語を特定します。
• 対応する2進数の数値を書き込みます。
• 1 を配置するためのアドレスとしてバイナリ値を使用します Kマップ内
• 他のminterm（Sum-Of-Products内のP-term）の手順を繰り返します。

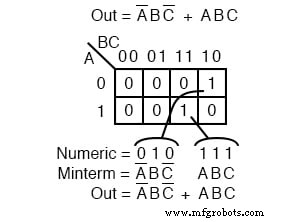
ブール式は、多くの場合、上記のようにカルノー図の複数のセルに対応する複数の最小項で構成されます。このマップの複数のmintermは、上の前の図で調べた個々のmintermです。

参考までにレビューするポイントは、 1 sは、1つ以上の積項に直接変換されるバイナリセルアドレスとしてKマップから出力されます。

直接意味するのは、 0 補完された変数に対応し、 1 真の変数に対応します。例： 010 A’BC ’に直接変換します 。

この例では減少はありませんでした。ただし、mintermsからのSum-Of-Productsの結果はあります。

上の図を参照して、KマップからSum-Of-Products縮小ブール方程式を作成する手順を要約します。

• 1 の最大のグループを形成する ■すべてのmintermをカバーする可能性があります。グループは2の累乗でなければなりません。
• グループの2進数値を書き込みます。
• バイナリ値を積項に変換します。
• 他のグループの手順を繰り返します。各グループは、Sum-Of-Products内のp項を生成します。

これまでのところ新しいことは何もありませんが、mintermsを処理するための正式な手順が書き留められています。これは、maxtermsを処理するためのパターンとして機能します。

次に、 0 であるブール関数を攻撃します 単一セルおよび 1 の場合 s他のすべての人のために。

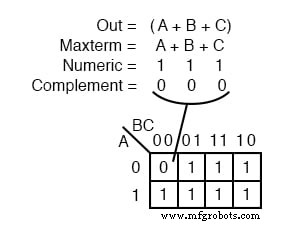
Maxterm

maxterm 0 になるブール式です。 単一細胞発現の出力用、および 1 ■カルノー図または真理値表の他のすべてのセル。左上の図は、maxterm （A + B + C）を示しています。 、単一の合計項、単一の 0 それ以外の場合は 1 であるマップ内 s。

maxtermに単一の 0 がある場合 残りのセルは 1 s、最大領域 1 をカバーしているように見えます s。

何か新しいmaxtermsを扱っているので、いくつかの違いがあります。 maxtermは 0 です 、 1 ではありません カルノー図で。 maxtermは合計項であり、（A + B + C） この例では、製品用語ではありません。 （A + B + C）も奇妙に見えます セル 000 にマッピングされます 。

方程式の場合 Out =（A + B + C）=0 、3つの変数すべて（A、B、C） 個別に 0 と等しくなければなりません 。 （0 + 0 + 0）=0 のみ 0 に等しくなります 。したがって、唯一の 0 を配置します 最小期間（A + B + C） セル内 A、B、C =000 Kマップでは、入力はすべて 0 。

これは、 0 を提供する唯一のケースです。 私たちのmaxtermのために。他のすべてのセルには 1 が含まれています s（（0,0,0）以外の入力値があるため （A + B + C）の場合 1 を生成します s評価時。

上の図を参照すると、Kマップにmaxtermを配置する手順は次のとおりです。

• マッピングする合計項を特定します。
• 対応する2進数の数値を書き込みます。
• 補集合を形成する
• 補数をアドレスとして使用して、 0 を配置します Kマップ内
• 他のmaxterms（Product-of-Sums式内のSum項）について繰り返します。

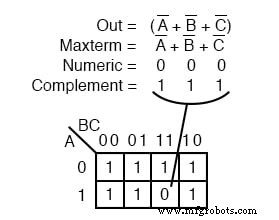
もう1つのmaxterm A ’+ B’ + C ’ 上に示されています。数値 000 A ’+ B’ + C ’に対応 。補数は 111 。 0 を配置します maxtermの場合（A ’+ B’ + C ’） このセル内（1,1,1） 上に示すようにKマップの。

なぜ（A ’+ B’ + C ’） 0 を引き起こします セル内にある 111 ？ A ’+ B’ + C ’の場合 は（1 ’+ 1’ + 1 ’） 、すべて 1 s in、つまり（0 + 0 + 0） 補数をとった後、 0 を与える唯一の条件があります 。すべての 1 sはすべての 0 に補完されます s、これは 0 またはの場合 ed。

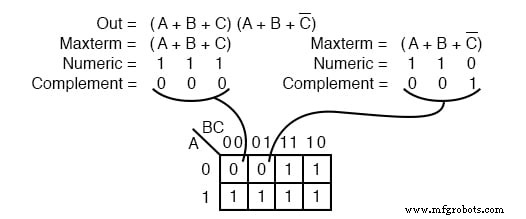
ブールのProduct-Of-Sums式またはマップには、上記のように複数のmaxtermが含まれる場合があります。 Maxterm （A + B + C） 数値の 111 を生成します これは 000 を補完します 、 0 を配置します セル内（0,0,0） 。 Maxterm （A + B + C ’） 数値の 110 を生成します これは 001 を補完します 、 0 を配置します セル内（0,0,1） 。

k-mapの設定が完了したので、私たちが本当に興味を持っているのは、Product-Of-Sumsリダクションの記述方法を示すことです。 0 を形成する sをグループに分けます。それは以下の2つのグループになります。 （0,0、X）である合計項に対応するバイナリ値を書き込みます 。

AとBはどちらも 0 グループのために。ただし、 C 両方とも 0 および 1 したがって、 X を記述します C のプレースホルダーとして 。補集合を形成する（1,1、X） 。合計項を書く（A + B） C を破棄する および X その場所を保持しました。

一般に、Product-Of-Sumsの結果では、より多くの合計項が乗算されると予想されます。ただし、ここに簡単な例があります。

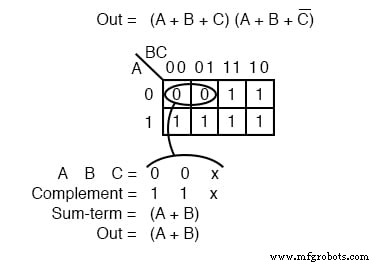
KマップのProduct-Of-Sumsブール代数削減を作成する手順を要約してみましょう。

• 0 の最大のグループを形成します s可能で、すべてのmaxtermsをカバーします。グループは2の累乗でなければなりません。
• グループの2進数値を書き込みます。
• グループの2進数値を補完します。
• 補数の値を合計項に変換します。
• 他のグループの手順を繰り返します。各グループは、Product-Of-Sums結果内の合計項を生成します。

例

例：

以下のProduct-Of-Sumsブール式を簡略化して、POS形式で結果を提供します。

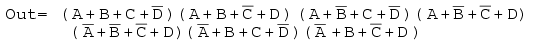
解決策：

7つのmaxtermsを 0 として下のマップに転送します s。適切なセルの場所を見つけるには、入力変数を補完するようにしてください。

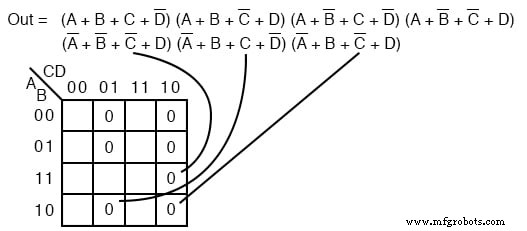
0 をマッピングします ■上のマップで左から右、上から下に表示されます。最後の3つのmaxtermを引出線で見つけます。

セルが上に配置されたら、下に示すようにセルのグループを形成します。グループが大きいほど、入力が少ない合計項が得られます。グループが少ないほど、結果の合計項が少なくなります。

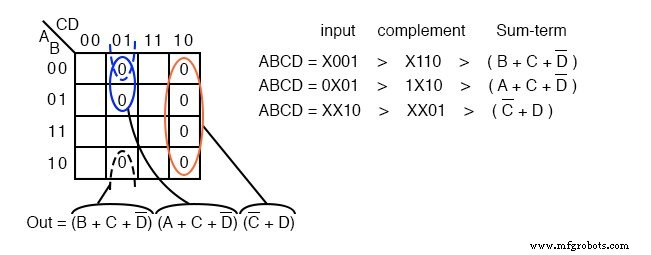
3つのグループがあるため、上記のPOS結果には3つの合計項があると予想されます。 4セルのグループは、2変数の合計項を生成します。 2セルの2つのグループは、2つの3変数の合計項を与えます。

上記の合計条件に到達した方法の詳細が示されています。グループの場合、バイナリグループの入力アドレスを書き込み、それを補完して、ブール和項に変換します。最終結果は、3つの合計の積です。

例：

以下のProduct-Of-Sumsブール式を簡略化して、SOP形式の結果を提供します。

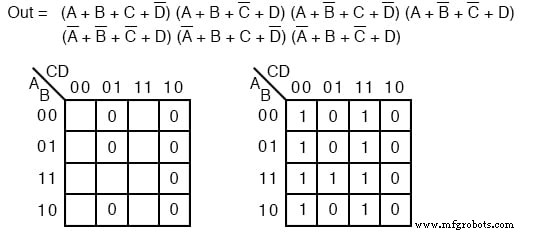
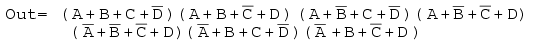
解決策： これは最後の問題の繰り返しのように見えます。ただし、完成したばかりのProduct-Of-Sumsではなく、Sum-Of-Productsソリューションを要求する点が異なります。 maxterm 0 をマップします 左下の前の問題のように与えられたProduct-Of-Sumsから。

次に、暗黙の 1 を入力します 右上の地図の残りのセルにあります。

1 のグループを形成する sすべての 1 をカバーする s。次に、この章の前のセクションのように、Sum-Of-Productsの簡略化された結果を記述します。これは前の問題と同じです。

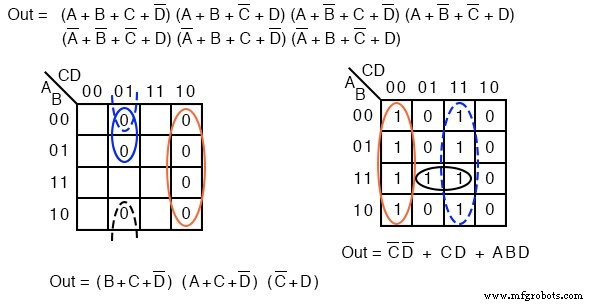
上に、前の例のProduct-Of-Sumsソリューションと、比較のために現在の問題のSum-Of-Productsソリューションの両方を示します。

より簡単な解決策はどれですか？ POSは3-ORゲートと1-ANDゲートを使用し、SOPは3-ANDゲートと1-ORゲートを使用します。どちらもそれぞれ4つのゲートを使用します。

よく見ると、ゲート入力の数を数えます。 POSは8入力を使用します。 SOPは7入力を使用します。最小コストソリューションの定義により、SOPソリューションはよりシンプルになります。

これは、現実の世界ではほとんど役に立たない、技術的に正しい答えの例です。

より良い解決策は、複雑さと使用されているロジックファミリによって異なります。 NANDゲートはSOP実装でうまく機能する基本的な構成要素であるため、TTLロジックファミリを使用する場合は通常、SOPソリューションの方が優れています。

一方、CMOSロジックファミリを使用する場合は、すべてのサイズのNORゲートが利用できるため、POSソリューションを使用できます。

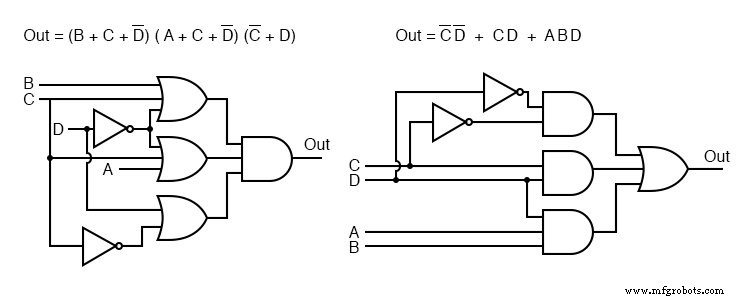
両方の場合のゲート図が上に示されています。左がProduct-Of-Sums、右がSum-Of-Productsです。

以下では、左側で繰り返されているサンプルロジックのSum-Of-Productsバージョンを詳しく見ていきます。

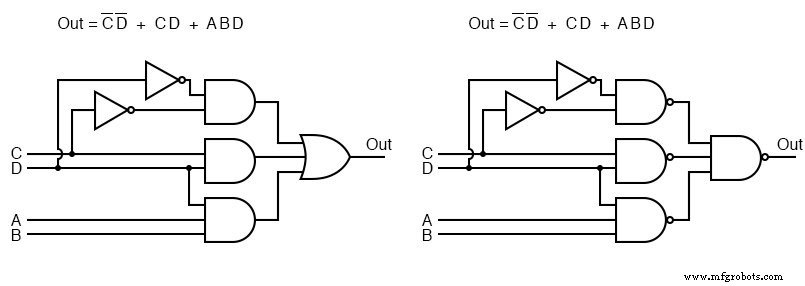
とりわけ、左側のANDゲートは右側のNANDゲートに置き換えられています。出力のORゲートはNANDゲートに置き換えられています。 AND-ORロジックがNAND-NANDロジックと同等であることを証明するには、右上から左下に示すように、3-NANDゲートの出力にあるインバーター反転バブルを最終的なNANDの入力に移動します。

>

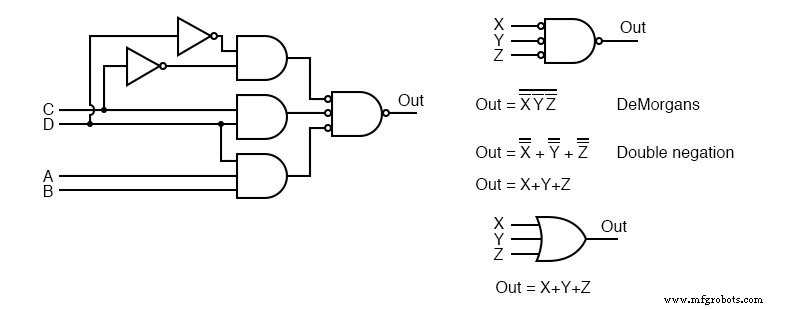
右上では、入力が反転した出力NANDゲートが、ド・モルガンの定理と二重否定によるORゲートと論理的に同等であることがわかります。

この情報は、TTLロジックファミリのNANDゲートが他のタイプよりもさまざまな構成で容易に利用できる実験室環境でデジタルロジックを構築するのに役立ちます。

AND-ORロジックの代わりにNAND-NANDロジックを構築する手順は次のとおりです。

• 削減された製品の合計ロジック設計を作成します。
• SOPの配線図を描くときは、すべてのゲート（ANDとORの両方）をNANDゲートに置き換えます。
• 未使用の入力はロジックHighに接続する必要があります。
• トラブルシューティングの場合、NANDゲート出力の第1レベルの内部ノードは、AND-ORダイアグラムの論理レベルと一致しませんが、反転されます。 NAND-NAND論理図を使用します。ただし、入力と最終出力は同じです。
• 複数のパッケージU1、U2などにラベルを付けます。
• データシートを使用して、すべてのゲートの入力と出力にピン番号を割り当てます。

例：

SOPの最小化に関する以前の問題を再検討してみましょう。 Product-Of-Sumsソリューションを作成します。 POSソリューションを以前のSOPと比較します。

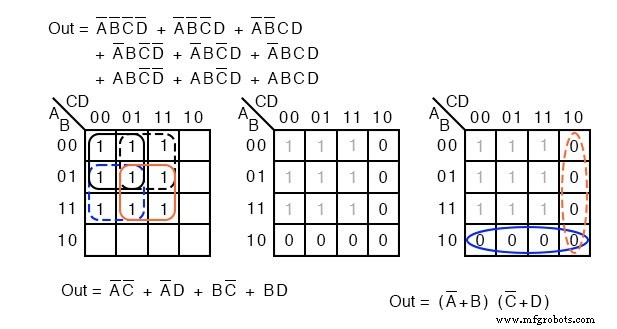
解決策：

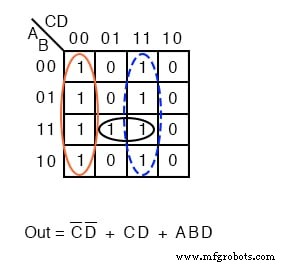
左上には、9分間のブールの単純化されていない式から始まる元の問題があります。確認したところ、左下の4製品期間のSOP結果を生成するために、4セルの4つのグループを形成しました。

上の中央の図では、空のスペースに暗黙の 0 を入力しています。 s。 0 sは4セルの2つのグループを形成します。青い実線のグループは（A ’+ B） 、赤い破線のグループは（C ’+ D） 。これにより、Product-Of-Sumsの結果に2つの合計項が生成されます。右上の Out =（A ’+ B）（C’ + D）

以前のSOPの簡略化（左）とPOSの簡略化（右）を比較すると、POSが最も低コストのソリューションであることがわかります。 SOPは合計5ゲートを使用し、POSは3ゲートのみを使用します。

このPOSソリューションは、結果が単純であるため、TTLロジックを使用する場合でも魅力的に見えます。 ANDゲートと2入力のORゲートを見つけることができます。

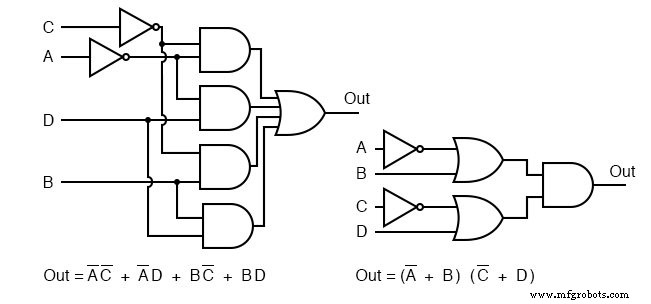
比較問題のために、SOPおよびPOSゲート図を上に示します。

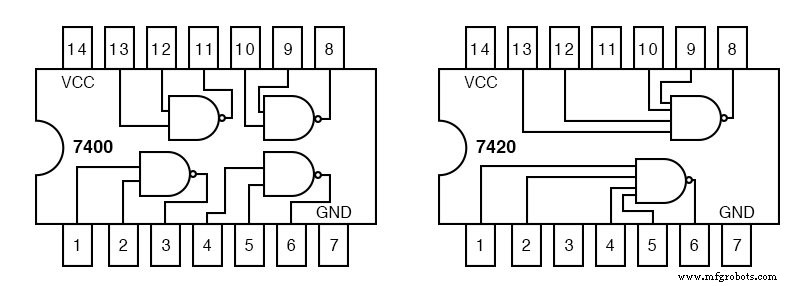
以下のTTLロジックファミリ集積回路ゲートのピン配置を前提として、右上のmaxtermダイアグラムに、回路指定子（U1-a、U1-b、U2-aなど）とピン番号のラベルを付けます。

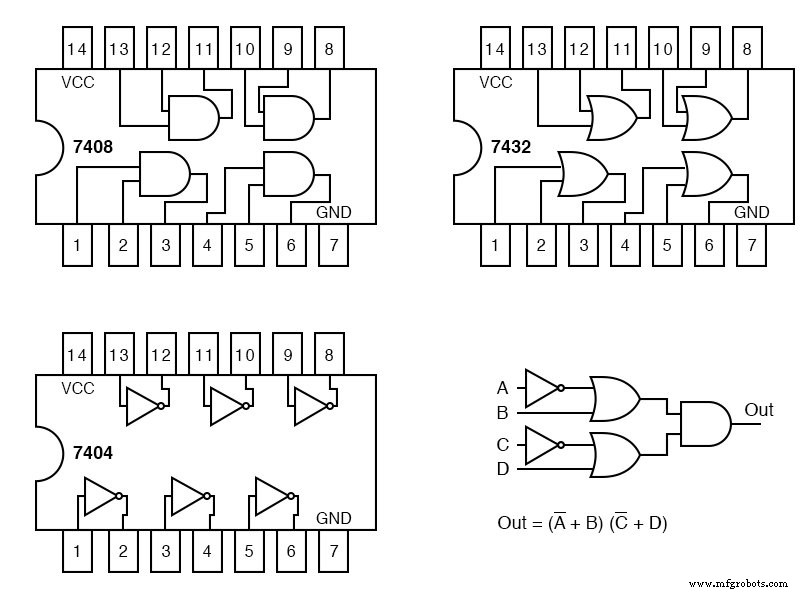
私たちが使用する各集積回路パッケージは、回路指定子U1、U2、U3を受け取ります。パッケージ内の個々のゲートを区別するために、それらはa、b、c、dなどとして識別されます。

7404hex-inverterパッケージはU1です。その中の個々のインバーターは、U1-a、U1-b、U1-cなどです。U2は7432クワッドORゲートに割り当てられます。 U3は7408クワッドANDゲートに割り当てられています。

上記のパッケージ図のピン番号を参照して、以下の回路図のすべてのゲート入力と出力にピン番号を割り当てます。

これで、この回路を実験室の設定で構築できます。または、プリント回路基板を設計することもできます。 それのための。プリント回路基板には、フェノールまたはエポキシグラスファイバーの非導電性基板で裏打ちされた銅箔の「配線」が含まれています。

プリント回路基板は、電子回路の大量生産に使用されます。未使用のゲートの入力を接地します。

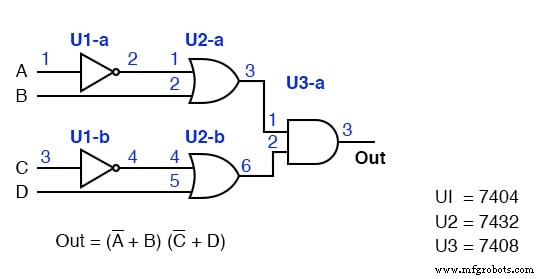
左上の前のPOSソリューション図（3番目の図の後ろ）に回路指定子とピン番号のラベルを付けます。これは、先ほど行ったことと似ています。

前の例では、2入力ANDゲート7408を見つけることができます。ただし、TTLカタログで4入力ORゲートを見つけるのに問題があります。

4入力の唯一の種類のゲートは右上に示されている7420NANDゲートです。

以下に示すように、NANDゲートへの入力を反転させることにより、4入力NANDゲートを4入力ORゲートにすることができます。したがって、入力を反転することにより、74204入力NANDゲートをORゲートとして使用します。

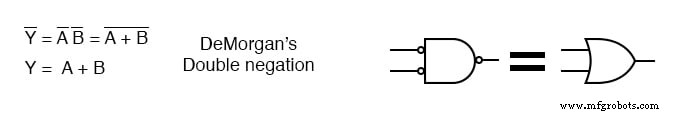
7420 4入力NANDゲートへの入力を反転するためにディスクリートインバーターを使用しませんが、SOP、minterm、ソリューションで要求されるANDゲートの代わりに2入力NANDゲートで駆動します。

2入力NANDゲートの出力での反転は、4入力ORゲートの反転を提供します。

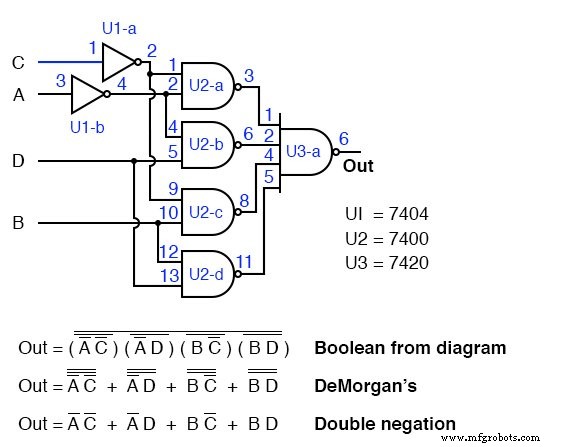
結果は上に示されています。 AND-ORロジックの代わりにNAND-NANDロジックを使用して、TTLゲートで実際に構築する唯一の実用的な方法です。

関連するワークシート：

• カルノーマッピングワークシート