原子間力顕微鏡によるナノスケールでのポリオレフィンエラストマーの定量的ナノメカニカルマッピング

はじめに

高度な重合技術の急速な進歩に伴い、ポリマーの形態とその機械的評価への関心が高まっています[1]。ポリマーの人気のあるクラスの1つはエラストマーです。エラストマーナノ構造は通常、明確な機械的役割を果たすことが期待されているため、それらの機械的特性は材料の性能に影響を与えるために極めて重要です。それらは通常、それらの特性において空間的および時間的不均一性を示します。それらのナノスケールの構造と特性が、最終的にバルク特性につながるマイクロ対応物にどのように関連しているかは完全には理解されていません[2、3、4、5、6、7、8]。それらの用途の広いアプリケーションでは、機械的特性を完全に理解する必要があります。ポリオレフィンエラストマー（PE）は、高電圧ケーブル[9]、ナノファイバー膜[10]、再利用可能な材料[11]、非混和性ポリマーシステム[12]など、多くの研究および産業分野で大きな関心を集めています。これは、ナノメカニカル測定のための効果的で信頼性の高いモデルポリマーシステムであることが証明されています[13、14]。その幅広い用途にもかかわらず、低密度PE（LDPE）の弾性率測定は、いくつかの理由で依然として困難です[15]。第一に、それらは粘弾性であり、それらの機械的応答は時間に依存することを意味します。第二に、大きな表面力は圧痕プロセスを複雑にします。第三に、接触力学を忠実に記述した堅牢なモデルはほとんどありません。 LDPEの機械的特性を測定するためにインデントを使用して複数の研究が行われています。 LDPEの弾性率を理解するために注目すべき進歩が達成されました。たとえば、温度[16]、線状低密度ポリエチレン[17]、ナノ粉末混合物[18]がヤング率にどのように影響するかが報告されています。ただし、これらの研究の大部分は高い空間分解能を欠いており、結果はナノスケールでの定量的特性評価への関心の高まりを満足させることはできません。多くの研究者は、原子間力顕微鏡（AFM）ベースの力測定などの代替技術に目を向けています[1,15]。

1980年代に発明されて間もなく、AFMは、サンプルの機械的特性を調べるための強力なツールとして確立されました。歴史的に、AFMは、Zピエゾ位置が傾斜しているときの垂直たわみの変化を追跡することができます。対応する力の荷重と除荷の軌道が記録されます（力-変位曲線）。次に、力-変位曲線は、さまざまな接触力学モデルに適合した力-距離曲線に処理されます。これは、単一の位置測定（単一のフォースランプ）またはマトリックスアレイ方式、いわゆるフォースボリューム（FV）のいずれかで実行できます。従来の力測定の適用は、サンプリングレートが遅いために非常に時間がかかります。これは、機器によって本質的に制限されます。遅い取得率は、高速フォースボリューム（FFV）と呼ばれる新しく造られた方法によって改善されました。 0.1Hzから約200Hzまで動作可能です。 FFVの基本的な動作メカニズムは、遷移時の三角駆動信号の平滑化に依存しており、アプローチとリトラクトの間の高速ターンアラウンドにつながります。前例のない技術的進歩にもかかわらず、力のサンプリングレートに関してはまだ改善の余地があります。ピークフォースタッピング（PFT）ベースの定量的ナノメカニカルマッピング（PFQNM）は、その高解像度イメージング機能とマッピングの機械的特性を同時に活用する新しいアプローチです。 PFQNMは、サンプリング速度を2 kHzまで上げることにより、通常のフォースボリュームを補完します。したがって、PFQNM、高速フォースボリュームと一緒にフォースボリュームは、フォースロード/アンロードレートの観点から4桁を占めます。前述のアプローチは、弾性率の測定という点で役立ちます。ヤング率。ただし、サンプルの動的な機械的動作はほとんどまたはまったく提供されません。ありがたいことに、AFMはクリープコンプライアンス実験と呼ばれる別のユニークな機能を提供します[19]。この設計では、AFMプローブはプリロード力でサンプル表面に接触します。次に、プローブは固定された力で静止したままになります。応力が一定である間、材料はクリープを受けます。 AFMは、時間の関数としてインデントの変化を監視します。取得したデータは、モデルの適合の対象となります。このような測定から、材料の動的機械特性に関する豊富な情報を抽出できます。上記のすべての技術を組み合わせれば、軟質ポリマーの時間依存の機械的特性を効果的に調査できる可能性があります。

フォースマッピングに加えて、PFTはトポグラフィーイメージングのための優れたツールです[20]。 PFTでは、Zピエゾがプローブホルダー全体を低周波数（通常は0.5k〜2k Hzの範囲）で上下に駆動します。柔らかいカンチレバーの垂直偏向に直接フィードバックを与えるため、力の優れた微調整を提供します。最大相互作用力を正常に制御する機能は、PeakForceタッピングとしてその名前が付けられました。さらに、高解像度と低侵襲性を維持します。これらの魅力的な特性により、PFTは柔らかい生体試料やポリマーサンプルのトポグラフィーイメージングにおける理想的な手法になっています。たとえば、ピークフォースタッピングモードは、導電性ポリマー間の接着力[21]と単一分子の生体認識イベント[22]を調査するためにうまく適用されています。現在まで、PFQNMは、硬化セメントペースト[23]、生細胞[24]、アミロイドフィブリル[25]、ポリマーマトリックス複合材料[26,27,28]など、さまざまな材料の機械的特性の特性評価に幅広い関心を集めています。およびさまざまなポリマー[29]。高解像度の高さ画像も収集されるため、局所的な機械的特性をナノスケールのサンプルトポグラフィーと相関させるのに便利です。

この研究では、LDPEサンプルの時間依存係数をいくつかのアプローチを利用して評価しました。具体的には、ランプ周波数は0.1〜2kHzまで個別に変更されます。厳密なキャリブレーションが行われ、データは適切なDerjaguin–Muller–Toporov（DMT）接触力学モデルに適合します。ランプ周波数の増加に伴い、ヤング率が増加することが発見されました。 LDPEの動的機械的挙動をさらに理解するために、クリープコンプライアンス実験が実施されました。瞬間弾性率 E ₁ 、遅延弾性率 E ₂ 、粘度η 、および遅延時間τ 標準のリニアソリッド（SLS）モデルフィットから抽出されました。マルチパラメトリック機械的測定と前例のない高空間分解能のトポグラフィーイメージングは​​、LDPEなどの軟質ポリマーの定量的ナノメカニカルマッピングにうまく利用されており、生物学的システムに拡張できる可能性があります。

材料と方法

資料

PeakForce QNMサンプルキットは、Bruker Co.（Santa Barbara、CA）から購入しました。キットには、ポリマーブレンドサンプル、サファイアサンプル、チップチェックサンプルが含まれていました。ポリマーブレンドサンプルは、低密度ポリオレフィン（LDPE）と混合されたポリスチレン（PS）の薄膜で構成されています。サンプルは両面テープを使用して金属パックにマウントされ、受け取ったままの状態で使用されました。製造によると、PSとLDPE（エチレン-オクテン共重合体）のブレンドがシリコン基板上にスピンキャストされ、さまざまな材料特性を持つフィルムが作成されました。 RTESPA-150プローブは、公称ばね定数5 N / mでBrukerCo。（Santa Barbara、CA）から購入しました。プローブカンチレバーの裏側は、レーザーのたわみを強化するために薄いアルミニウム層でコーティングされていました。

キャリブレーション

ScanAsystモードを備えたDimensionICON AFM（Bruker Co.、Santa Barbara、CA）を使用して、キャリブレーションと機械的測定を行いました。カンチレバーのたわみ感度、カンチレバーのばね定数、および先端の半径のキャリブレーションが、フォースランプとフォースボリュームに対して実行されました。この研究では、同じバッチの3つのプローブを使用しました。校正プロトコルは次のとおりです。カンチレバーのたわみ感度は、RTESPA-150プローブを非常に硬い表面（この場合はサファイアサンプル）に持ってくる、いわゆるタッチキャリブレーションアプローチを介してフォースランプを実行することによってキャリブレーションされました。ランプ出力はZ用に選択されました。ランプサイズは200nmに維持され、相対トリガーしきい値はベースラインバックグラウンドより0.3V上に固定されました。力対Zピエゾ変位曲線が収集された後、接触領域の最も線形な部分を定義するために1対の線が使用されました。偏向感度の更新をクリックすると、偏向感度が自動的に調整されて保存されます。測定された偏向感度は44.7±4.2nm / V（ n =3）。次に、熱エネルギーによる自由空気中のカンチレバーの振動スペクトルを取得するために、熱調整が実行されました。共振周波数のピークは、AFMメーカー（Bruker Co. Santa Barbara、CA）が提供するリアルタイムNanoScopeソフトウェアによって強調表示され、適合されました。等分配の定理の理論に基づいて、

ここで、\（k _ {{\ text {B}}} \）はボルツマン定数、\（T \）はケルビン単位の絶対温度、\（d \）は片持ち振動振幅の二乗平均平方根値です。ばね定数\（k \）は、1.09の補正係数を考慮して適宜計算されました。チップ半径は、チップチェックサンプル全体でプローブを注意深くスキャンすることによって推定されました。サンプルは、一部の領域に先のとがった端を持つチタンで構成されています。それぞれの鋭い端は、先端の形状の一部をキャプチャします。結局、サンプルの地形画像を使用して、球であると推定された先端の形状を再構築することができました。先端の半径を正確に推定するには、くぼみの深さも必要でした。インデントの深さ（18.3±2.6 nm、 n =3）は、ゼロ分離と接触ジャンプの最低点との間の距離を測定することによって得られました。これにより、チップチェック画像の頂点からの高さ1のくぼみの値を代入することにより、有効なチップ半径が調整されました。

同期距離とPFT振幅感度は、PFQNM技術に固有のものです。それらも較正する必要があります。同期距離は、Zピエゾが最低位置に到達する時定数として定義されます。 PFT振幅感度は、デジタル入力された駆動信号を物理的にZピエゾ変位に転送するスケーリング係数と呼ばれます。その精度により、Zピエゾが希望どおりに動くことが保証されます。同期距離とPFT振幅感度の両方が、タッチキャリブレーションアプローチを使用してサファイアサンプルでキャリブレーションされました。特に、同期距離とPFT振幅感度は周波数に依存します。両方とも離散周波数で校正されました。この作業では、0.125k〜2kHzの幅広い周波数が選択されました。

PFQNM定量的ナノメカニカルマッピング

RTESPA-150プローブは、LDPEサンプルの定量的ナノメカニカルマッピングのためにロードされました。校正されたばね定数は3.9±1.4N / m（n =3）でした。スキャン時に、ユーザーは力の設定値を5 nNに設定し、ScanAsystに自動制御させて、イメージング取得レート（スキャンレート）、フィードバックゲイン、およびZ範囲を最適化します。デジタルピクセルは、画像あたり256×256に保たれました。 PFT周波数は、実験間で2kから0.125k Hzまで変化し、時間に依存する力のロードとアンロードを生成しました。 2 kHzPFT周波数で100nm PFT振幅の場合、対応する力負荷率は0.8 mm s ^-1 でした。 。粘弾性LDPEのポアソン比は0.35と仮定されました[13]。 5 µm×5 µmの調査領域が、地形と機械的測定と同時にスキャンされました。 NanoScopeコントローラーには、機械的データを計算してリアルタイムのソフトウェアチャネルで表示するのに十分な帯域幅がありました。これらのデータは、さらにオフラインで分析するために生の画像に保存されました。したがって、高さセンサー、DMT係数、接着マップ、インデント、エネルギー散逸チャネルなど、多数の画像チャネルがキャプチャされました。 LDPEとポリスチレンのコンポーネントが特定されたら。 LDPEでの高空間分解能PFQNM測定は、0.5 µm×0.5 µmスキャンで実行されました。

AFMフォースランプとファストフォースボリューム

カンチレバーの垂直偏向を監視しながら、Zピエゾ変位を傾斜させることにより、力の傾斜と高速の力の体積を実現しました。ランプサイズは200nmでした。 5 nNでの低いトリガー力の設定値は、ランププロセス中のたわみドリフトを排除する一定のバックグラウンド減算メカニズムによって達成されました。フォースランプサンプリングアレイは、0.5 µm×0.5 µmの領域で定義されました。ランプレートは0.1Hz、1 Hz、10 Hz、20 Hz、61 Hz、122Hzでした。 1Hzのランプ速度と200nmのランプサイズの場合、対応する力の負荷速度は400 nm s ^-1 でした。 。 0.1Hzと1Hzで16×16のランプ曲線が収集され、10 Hz、20 Hz、61 Hz、122Hzで128×128のランプ曲線が収集されました。

クリープ実験

スターゲートスキャナーは、クリープ実験用にドリフトキャリブレーションされました。 RTESPA-150プローブは、2 nNで事前設定された力の負荷に達するまで、PS / LDPEサンプルのニートなLDPE領域に接触させられました。 NanoScopeソフトウェアの表面制御機能により、プローブをサンプル上に一定期間（この場合は5秒間）保持できます。この期間はホールドセグメントと名付けられました。トリガー力を保持することにより、加えられた力を一定に維持した。保留セグメントについては、124個のデータポイントが収集されました。高さセンサー対時間およびたわみ誤差（力）対時間の両方が取得されました。ランダムに選択された場所で少なくとも50のクリープ曲線がキャプチャされました。 3つの独立した実験が行われた。サファイアサンプルに対してブランクコントロール実験を実施しました。予想通り、Zに目立った変化は見られませんでした。

実験的な設定

LDPEサンプルの機械的特性を定量的にマッピングするために（図1）、実験は、鋭いカンチレバーの先端がLDPEサンプルに押し込まれ、事前設定された力の負荷が達成されたときにサンプル表面から引き離されるように設計されました（図1a）。力は、位置敏感フォトダイオード（PSPD）で垂直偏向信号を検出することによって記録されました。カンチレバーの動きは、Zピエゾの動きによって駆動されました。技術の選択に応じて、駆動信号は三角波（FV）、角丸三角波（FFV）、または正弦波信号（PFQNM）になります。 PFQNMは図1bに概略的に描かれており、力と時間の曲線は、サンプル表面に近づくとチップがスナップイン接触し、サンプル表面から離れるときにチップがスナップアウトすることを明確に示しています。同期距離は、アプローチカーブをリトラクトカーブから分離するターニングポイントを定義しました。硬い表面では、この点はZピエゾが最低位置に達したときの時定数でした。また、力がピーク力に達したときも意味します。対照的に、ソフトコンプライアントサンプルでは、​​時間に依存するサンプルの変形により、このポイントが少しシフトする可能性があります。採用された手法に関係なく、AFMは力対Z変位曲線を記録し、さらに力対チップ-サンプル分離曲線に変換されました（図1c）。収縮曲線の接触部分は、以下に説明する線形化されたDMTモデルに適合され、DMT係数が抽出されました。エネルギー散逸は、ヒステリシスループを統合することによって計算されました。カンチレバーの先端がサンプルにインデントできるように、また十分な力の感度が得られるように、適切なばね定数を持つカンチレバーが慎重に選択されました。一方、加えられる応力は接触面積にも依存するため、先端の半径も考慮する必要があります。これらに照らして、RTESPA-150プローブが選択されました。これは、サンプルにインデントするのに適切な量の力を生成すると同時に、高い力感度を維持するためです。

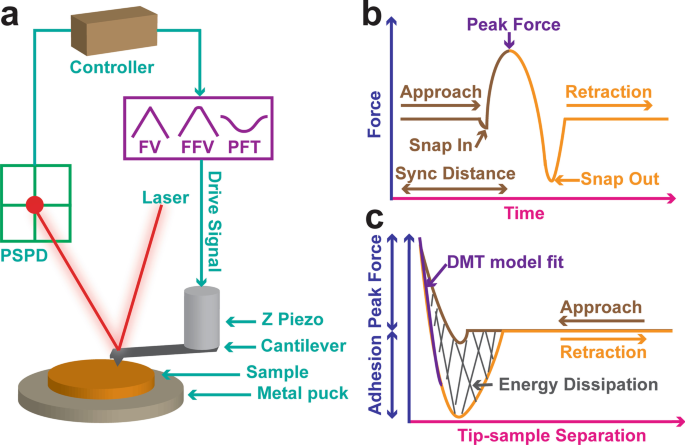
AFMフォースランプのメカニズム、実験計画、データ取得および解釈。 LDPEサンプルを金属パックにマウントしました。鋭いカンチレバーの先端がLDPEサンプルに押し込まれ、事前に設定された力に達すると引き込まれます（ a ）。レーザーが上から光り、カンチレバーの裏側に当たって偏向しました。偏向信号は、位置敏感フォトダイオード（PSPD）によって受信されました。カンチレバーの動きは、取り付けられたZピエゾによって駆動されました。技術の選択に応じて、駆動信号は三角波（FV）、角丸三角波（FFV）、または正弦波（PFQNM）になります。 PFQNM力の測定は、 b に概略的に示されています。 、力対時間のプロットは、サンプル表面に近づけたときにチップがスナップイン接触し、サンプル表面から引き離したときに接触がスナップアウトしたことを明確に示しています。同期距離は、高さセンサーが最低位置に到達する時定数でした。力対Z変位曲線（F-Z）はAFMによって記録され、さらに力対チップ-サンプル分離（F-D）曲線に変換されました（ c ）。 DMT弾性率は、収縮曲線の接触部分をDMTモデルに適合させることによって抽出されました。ヒステリシスループ上の積分は、エネルギー散逸と呼ばれていました

データ分析

オフラインデータ分析は、AFMファクトリーが提供するNanoScope Analysisソフトウェア（Bruker Co.、カリフォルニア州サンタバーバラ）を使用して実施しました。すべての地形画像は、Zピエゾドリフト、バックグラウンドノイズを取り除き、サンプルの傾きを補正する一次平坦化の対象となりました。表面粗さは、NanoScopeAnalysisソフトウェアが提供する表面粗さ機能によって評価されました。

ここで、\（N \）は画像領域内のポイントの総数、\（Z _ {{\ text {i}}} \）は i の\（Z \）の高さです。 データポイントであり、\（Z _ {{\ text {m}}} \）は、領域全体の平均\（Z \）高さです。すべての機械的データ画像は、平準化せずにそのまま残されました。

フォースランプ、高速フォースボリューム、およびPFQNMの両方で、フォース対Zピエゾ変位（F-Z）曲線が得られました。力対チップ-サンプル分離（F-D）曲線は、より物理的に意味があり、モデルの適合に要求されます。 Z変位は、3つのコンポーネント、つまりチップとサンプルの分離（ D ）で構成されます。 ）、カンチレバーのたわみ（ d ）、およびインデントの深さ（\（\ delta \））。 F-ZからF-Dに変換するには、カンチレバーのたわみを差し引く必要があります（ d ）、およびZ変位からのインデントの深さ（\（\ delta \））。カンチレバーのたわみ感度とばね定数が較正されていれば、リアルタイム制御ソフトウェアまたはオフラインデータ分析ソフトウェアのいずれかで実行できます。さらに、ベースライン補正機能を実行して、力曲線のベースラインをゼロにオフセットしました。最後に、F-D曲線が取得され、DMTモデルの適合が行われました。ヘルツ接触理論によると、

ここで、\（F _ {{{\ text {appl}}}} \）は、チップがサンプルに加えた力です。付着力（\（F _ {{{\ text {adh}}}} \））が考慮されます。 \（R \）は、推定される球の先端の先端半径です。 \（\ delta \）はインデントの深さです。 \（E _ {{\ text {r}}} \）は、減少したヤング率です。チップとサンプルの係数に関連しています

ここで、\（v _ {{\ text {s}}} \）と\（v _ {{\ text {t}}} \）は、それぞれサンプルとAFMチップのポアソン比です。 \（E _ {{\ text {s}}} \）と\（E _ {{\ text {t}}} \）は、それぞれサンプルとAFMチップのヤング率です。チップのヤング率はLDPEサンプルのヤング率よりも数桁大きいため、チップの項は無視できます。 \（E _ {{\ text {r}}} \）と\（v _ {{\ text {s}}} \）がわかれば、\（E _ {{\ text {s}}} \）を簡単に知ることができます計算されます。

式の両側を取ることによって。 （3）\（F _ {{{\ text {appl}}から\（F _ {{{\ text {adh}}}} \）を引いた後の\（\ frac {2} {3} \）乗}} \）、線形化されたモデルがすべての力データに適合するために採用されました[30]。このモデルでは、接点を特定する必要はありません。

次に、\（E _ {{\ text {r}}} \）と\（E _ {{\ text {s}}} \）が結果として抽出されました。

カンチレバーはばねのように機能するため、加えられる力はフックの法則から計算されました。

ここで、\（k \）はカンチレバーのばね定数、\（d \）はカンチレバーのたわみであり、カンチレバーのたわみ感度に垂直たわみ信号を掛けて計算されます。

クリープコンプライアンス解析には、SLSモデルのVoigtバージョンが採用されました[19]。この3要素モデルでは、ばね（ E ₁ ）はばね（ E ）と直列になっています ₂ ）-ダッシュポットVoigt要素を並列に。圧縮距離（ d ）時間の関数として、次のように説明できます。

ここで F は総荷重力、 k ₁ および k ₂ E の弾力性です ₁ および E ₂ 、 それぞれ。 η ダッシュポットの粘度を表します。チップとサンプルの相互作用領域は有限領域であるため、単一の点ではありません。モデルは、応力、ひずみ、弾性率の観点から方程式を書き直すことで改善できます。この研究では、Lamらによって開発された方法が採用されました。それらの類似した方程式は次のとおりです。

ここで、ε （ t ）は、ひずみを関数時間として示します。σ ストレスです。 E ₁ および E ₂ それぞれ、瞬間弾性係数と遅延弾性係数です。 η ダッシュポットの粘度を表します。さらに、ストレスσ ひずみε モジュラス E に関連しています またはコンプライアンス D 次の関係によって。

したがって、式（9）は次のように書き直すことができます。

ここで D および E システムのクリープコンプライアンスと複合弾性率をそれぞれ示します。式を書き直します。 （5）as

式を代入します。 （11）式に（12）は

クリープデータは、式（1）でフィッティングできます。 （13）および遅延時間τ

遅延時間は、クリープの〜63％が発生した時間と呼ばれます。

すべての力の測定は3回繰り返されました。結果は平均±SD（標準偏差）の形式で報告され、独立した実験の数は n として示されました。 =3。

結果

PFQNMの有効性と精度を評価するために、5 µm×5 µmの大規模な調査スキャンが実行されました。 2kHzでのPS / LDPEブレンドサンプルの代表的なPFQNM画像を図2にまとめました。図2a〜dは、高さセンサー画像、DMTモジュラスチャネル、インデントチャネル、およびエネルギー散逸チャネルです。平坦な領域はPSコンポーネントであり、膨らんだ領域はLDPEでした（図2a）。調査スキャンが完了すると、AFMは、LDPE領域を物理的に拡大し、高解像度の小さいサイズ（1.3 µm×1.3 µm）のスキャンを行うように指示されました。対応する画像チャネルが図2e–hに表示されました。

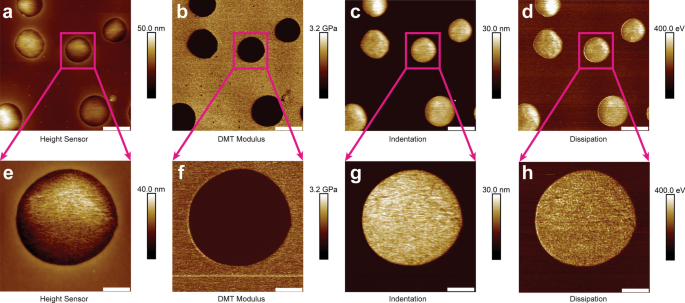
2kHzでのPS / LDPEブレンドサンプルの代表的なPFQNMナノメカニカルマッピング（5 µm×5 µm）。パネル a – d 高さセンサー画像、DMTモジュラスチャネル、インデントチャネル、およびエネルギー散逸チャネルです。画像の場合 a – d 、スケールバーは1 µmを表します。サーベイスキャンが完了すると、AFMはLDPE領域を物理的に拡大し、高解像度の小さなサイズ（1.3 µm×1.3 µm）のスキャンを行うようにガイドされます。対応する画像チャンネルがパネル e–h に表示されます 。スケールバーは、パネル e の260nmを表します – h

次に、PFQNM、FV、およびFFVが、0.5 µm×0.5 µmのニートなLDPE領域で実行されました。図3a〜dに、2kHzでのPFQNMの代表的なセットを収集しました。それらには、高さセンサー、弾性率マッピング、エネルギー散逸、およびくぼみが含まれていました。高さセンサー画像の表面粗さは、\（R _ {{\ text {q}}} \）の形式で2.58±0.35nmと報告されました。 122 HzでのFFVの別の代表的なセットを図3e、fに示しました。 FVとFFVにはエネルギー散逸とインデントチャネルがなかったことに注意してください。さまざまな周波数での弾性率が一緒にプールされました（図3g）。ヤング率のデータを表1に示します。0.1Hz、1 Hz、10 Hz、20 Hz、61 Hz、122 Hz、125 Hz、250 Hz、500 Hz、1 k Hz、2 kHzでのヤング率は11.7±でした。 5.2 MPa（ n =3）、18.2±5.6 MPa（ n =3）、25.4±6.8 MPa（ n =3）、29.6±8.4 MPa（ n =3）、33.8±9.7 MPa（ n =3）、35.7±10.5 MPa（ n =3）、43.8±10.7 MPa（ n =3）、54.8±11.9 MPa（ n =3）、66.7±13.6 MPa（ n =3）、80.9±14.2 MPa（ n =3）、89.6±17.3 MPa（ n =3）、それぞれ。散布図は、Origin8.5ソフトウェアを使用して生成されました。データは、\（E =15.31 \ times f ^ {{0.23}} \）（\（R ^ {2} \）=0.96）を生成するべき関数で近似されました。エネルギー散逸とさまざまなマッピング周波数の関係を図3hにプロットしました。 2 kHz、1 kHz、0.5 kHz、0.25 kHz、および0.125 kHzで得られたエネルギー散逸値は、173.2±21.9 eV（ n ）でした。 =3）、213.8±32.7 eV（ n =3）、233.9±29.3 eV（ n =3）、261.1±33.5 eV（ n =3）、293.2±35.6 eV（ n =3）、それぞれ。データは、\（E _ {{{\ text {diss}}}} =202.83 \ times f ^ {{--0.18}}〜\）（\（R ^ {2} \）=0.97 ）。代表的なF-D曲線は、LDPEサンプル表面からのAFMチップの2つの異なる破裂を示しました（図3i）。複数の破裂の発生は、より低い周波数、つまり0.1〜1Hzでより頻繁に発生しました。

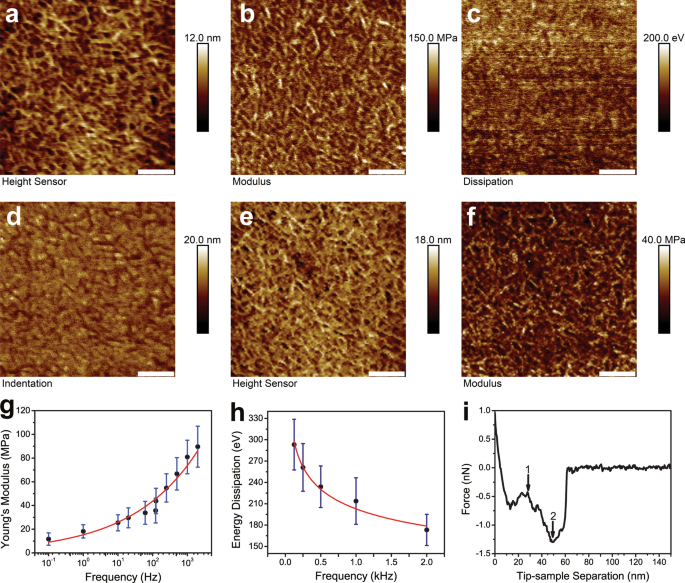
さまざまな周波数でマッピングされたLDPEサンプルの機械的特性。パネル a – d 高さセンサー画像、DMTモジュラスチャネル、エネルギー散逸、およびインデントチャネルは、適切なLDPE領域で2kHzのPFQNMでキャプチャされました。高さセンサー画像の表面粗さは、\（R _ {{\ text {q}}} \）の形式で2.58±0.35nmと報告されました。パネルeとfは、高さセンサーの画像と、ニートなLDPE領域で122HzのFFVでキャプチャされたDMTモジュラスチャネルです。画像の場合 a – f 、スケールバーは100nmを表します。測定されたヤング率（ E ）間の関係 ）および力のマッピング頻度（ f ）は g でプロットされました 。さまざまな周波数で測定されたヤング率を表1に示します。データは、\（E =15.31 \ times f ^ {{0.23}} \）（\（R ^ {2} \）=0.96 ）。エネルギー散逸の関係（ E _diss ）およびさまざまなマッピング頻度（ f ）はパネル h に表示されました 。 2 kHz、1 kHz、0.5 kHz、0.25 kHz、0.125 kHzで得られたエネルギー散逸値は、それぞれ173.2±21.9 eV、213.8±32.7 eV、233.9±29.3 eV、261.1±33.5 eV、293.2±3でした。データは、\（E _ {{{\ text {diss}}}} =202.83 \ times f ^ {{--0.18}}〜\）（\（R ^ {2} \）=0.97 ）。代表的なF-D曲線は、LDPEサンプル表面からのAFMチップの2つの異なる破裂を示しました（パネル i ）。複数の破裂の発生は、より低い周波数、つまり0.1〜1Hzでより頻繁に発生しました

最後に、クリープコンプライアンス測定がPS / LDPEサンプルのニートLDPE領域で実行されました。 AFMクリープ実験の動作原理を図4aに示しました。最初に、事前定義された力の設定値に達するまで、AFMチップをサンプル表面に接触させました。チップをサンプルに一定時間保持し、その間力を一定に保ちました。その後、チップが引っ込められました。ホールドセグメントでは、AFMはZモーションの変化を記録しました。時間の関数としてのくぼみの深さの変化（図4b）は、式（1）を使用してSLSモデルのVoigtバージョンに適合させることができます。 （13）。代表的なクリープ曲線を図4cに示しました。黒い曲線はデータであり、赤い実線はフィッティング曲線です。挿入図は、スプリング（ E ）を備えたSLSモデルのVoigtバージョンを示しています。 ₁ ）スプリングと直列に（ E ₂ ）-ダッシュポット（η ）並列のVoigt要素。実験では、瞬間弾性係数 E ₁ 、遅延弾性率 E ₂ 、粘度η 、遅延時間τ それぞれ22.3±3.5MPa、43.3±4.8 MPa、38.7±5.6 MPa、0.89±0.22秒でした。データは表2にまとめられています。

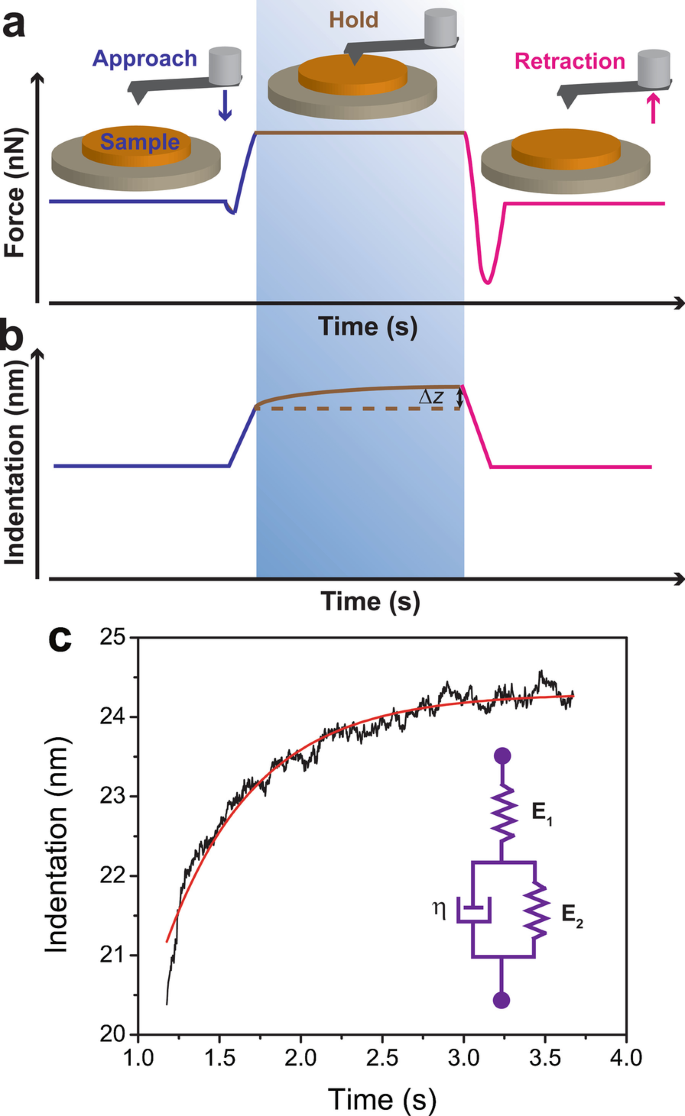
PS / LDPEサンプルのニートLDPE領域でのクリープコンプライアンス測定。 AFMクリープ実験の動作原理は、パネル a に示されています。 。最初に、AFMチップは、事前定義された力の設定値に達するまでサンプル表面に接触させられました。次に、チップをサンプルに一定時間保持し、その間、力を一定に保ちました。その後、チップが引っ込められました。ホールドセグメントでは、AFMはZモーションの変化を記録しました（パネル b ）。時間の関数としてのくぼみの深さの変化は、式（1）を使用してSLSモデルのVoigtバージョンに適合させることができます。 （13）。代表的なクリープ曲線がパネル c に示されています 。黒い曲線はデータであり、赤い実線はフィッティング曲線です。挿入図は、スプリング（ E ）を備えたSLSモデルのVoigtバージョンを示しています。 ₁ ）スプリングと直列に（ E ₂ ）-ダッシュポット（η ）並列のVoigt要素

ディスカッション

本研究では、ポリマーサンプル用の包括的で強力なナノメカニカルマッピングアプローチが、多数のナノスケールAFMベースの力測定を組み込むことによって開発されました。このアプローチにより、高解像度のトポグラフィーイメージングと定量的なナノメカニカルマッピングを同時に行うことができます。局所的な機械的挙動は、サンプルのトポグラフィーと相関させることができます。さらに重要なことに、軟質粘弾性材料の時間依存の機械的応答がうまくマッピングされています。ヘルツモデルは、広く受け入れられている接触力学モデル[31]であり、剛性プローブが半無限、等方性、均質な弾性表面をインデントするシナリオが説明されています。ただし、ヘルツモデルは表面力を想定していないため、柔らかい材料には当てはまりません。この欠点を克服するために、Johnson–Kendall–Roberts（JKR）モデルとDMTモデルが開発されました。この研究の設定を考えると、長距離の表面力が存在する場所では、弾性率が高く、接着力が低く、先端の半径が小さいため、DMTモデルを実装できます。 5 nNでの力の設定値は経験的に得られており、DMTモデルが保持されている間に意味のあるくぼみの深さを得るという点で最適値であることが正当化されています。低い力の負荷はまた、塑性領域ではなく弾性領域でサンプルの変形を引き起こします。さらに、鋭い先端により、PFQNM測定での高解像度のサンプルトポグラフィイメージングが可能になります。これは、サンプルトポグラフィを機械的特性と相関させる場合に魅力的な利点です。

先端半径の推定は、定量的な機械的測定では簡単ではありません。多くの研究では、既知の弾性率を持つサンプルを使用した逆算によって先端半径を推定しています[29、32]。この作品は、そのようなサンプルを必要としない別の再構築戦略を採用しています。鈍い先端を使用すると、より厳密な弾性率の数値が得られる傾向があり、鋭い先端は弾性率を過大評価する可能性があることが文書化されています。ただし、鋭い先端は高い空間分解能を維持します。これは、他の手法にはない利点です。ポリマーフィブリルがはっきりと見られます（図3の0.5 µm×0.5 µmスキャンを参照）。鋭い先端は、小さな負荷の下でも、大きな応力のためにコンプライアントサンプルに浸透し、大きなくぼみを生じる可能性があります。したがって、DMTモデルの有効性が損なわれる可能性があります。加えられた力は正確かつ敏感な方法で制御されるため、この研究ではそうではありません。これは、結果として生じるくぼみの深さと同じ桁の有効な先端半径（22.5±3.2 nm、 n =3）。 LDPE高さ画像の表面粗さ（\（R _ {{\ text {q}}} \））は2.58±0.35 nmであり、表面が平坦であり、表面粗さが定量的測定の交絡因子として扱われるべきではないことを示しています[33 ]。さらに、線形化されたDMTモデルの適合では、最終的に計算された弾性率に大きな誤差をもたらす可能性のある接触点の決定は必要ありません[34]。まとめると、現在の実験設定はDMTモデルを満たしています。