







Simulink は、MATLAB と統合された動的および組み込みシステム用のシミュレーションおよびモデルベースの設計環境です。同じく MathWorks によって開発された Simulink は、マルチドメイン動的システムのモデリング、シミュレーション、および解析のためのデータ フロー グラフィカル プログラミング言語ツールです。これは基本的に、ブロック ライブラリのカスタマイズ可能なセットを備えたグラフィカルなブロック ダイアグラム ツールです。 これにより、MATLAB アルゴリズムをモデルに組み込み、さらに分析するためにシミュレーション結果を MATLAB にエクスポートできます。
GNU Octave は MATLAB のような高水準プログラミング言語であり、MATLAB とほとんど互換性があります。数値計算にも使用されます。 Octave は MATLAB と以下の共通機能を持っています − 行列は基本的なデータ型です 複素数のサポートが組み込まれています 数学関数とライブラリが組み込まれています ユーザー定義関数をサポート GNU Octave は自由に再配布可能なソフトウェアでもあります。 Free Software Foundation によって発行された GNU General Public License (GPL) の条件に基づいて、再配布および/

MATLAB には、ラプラス変換やフーリエ変換などの変換を操作するためのコマンドが用意されています。変換は、分析を簡素化し、データを別の角度から見るためのツールとして科学と工学で使用されます。 たとえば、フーリエ変換を使用すると、時間の関数として表される信号を周波数の関数に変換できます。ラプラス変換により、微分方程式を代数方程式に変換できます。 MATLAB は laplace を提供します 、フーリエ そしてfft ラプラス、フーリエ、高速フーリエ変換を操作するコマンド。 ラプラス変換 時間 f(t) の関数のラプラス変換は、次の積分によって与えられます − ラプラス変換は、f(t
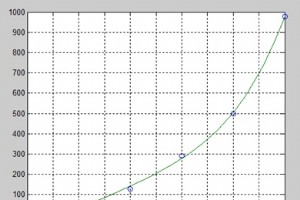
MATLAB は多項式を、降べきの順に並べられた係数を含む行ベクトルとして表します。たとえば、方程式 P(x) =x4 + 7x3 - 5x + 9 は − と表すことができます p =[1 7 0 -5 9]; 多項式の評価 ポリヴァル 関数は、指定された値で多項式を評価するために使用されます。たとえば、前の多項式 p を評価するには 、x =4で、タイプ- ライブデモ p = [1 7 0 -5 9]; polyval(p,4) MATLAB は上記のステートメントを実行し、次の結果を返します − ans = 693 MATLAB は polyvalm も提供します 行列

統合は、本質的に異なる 2 つのタイプの問題を扱います。 最初のタイプでは、関数の微分が与えられ、関数を見つけたいと考えています。したがって、基本的に微分のプロセスを逆にします。この逆のプロセスは、反微分、原始関数の発見、または不定積分の発見として知られています。 . 2 番目のタイプの問題は、非常に多数の非常に小さな量を合計し、項の数が無限になる傾向がある一方で、量のサイズがゼロに近づくにつれて極限を取ることを伴います。このプロセスは、定積分の定義につながります . 定積分は、面積、体積、重心、慣性モーメント、力によって行われる仕事、および他の多くの用途を見つけるために使用
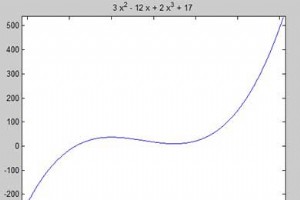
MATLAB は diff を提供します 記号導関数を計算するコマンド。最も単純な形式では、微分したい関数を引数として diff コマンドに渡します。 たとえば、関数 f(t) =3t2 の導関数を計算してみましょう。 + 2t-2 例 スクリプト ファイルを作成し、次のコードを入力します − syms t f = 3*t^2 + 2*t^(-2); diff(f) 上記のコードをコンパイルして実行すると、次の結果が生成されます − ans = 6*t - 4/t^3 以下は、上記の計算に相当するオクターブです- pkg load symbolic symbols t =
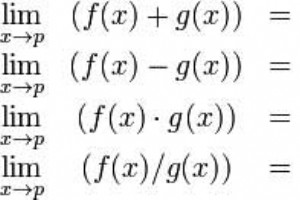
MATLAB は、微分および積分計算の問題を解くためのさまざまな方法を提供し、任意の次数の微分方程式を解き、極限を計算します。何よりも、元の関数とその導関数を解くことで、複雑な関数のグラフを簡単にプロットし、グラフ上の最大値、最小値、およびその他の定常点を確認できます。 この章では、微積分の問題を扱います。この章では、計算前の概念、つまり関数の極限の計算と極限の特性の検証について説明します。 次の章では差分 、式の導関数を計算し、グラフの極大値と極小値を見つけます。微分方程式の解法についても説明します。 最後に、統合で の章では、積分計算について説明します。 制限の計算 MATLAB

これまでのところ、すべての例が MATLAB とその GNU (代わりに Octave と呼ばれる) で機能することを確認しました。ただし、基本的な代数方程式を解く場合、MATLAB と Octave はほとんど変わらないため、MATLAB と Octave については別のセクションで説明します。 また、代数式の因数分解と単純化についても説明します。 MATLAB で基本的な代数方程式を解く 解決 関数は、代数方程式を解くために使用されます。最も単純な形式では、solve 関数は引用符で囲まれた式を引数として受け取ります。 たとえば、式 x-5 =0 の x について解いてみましょう
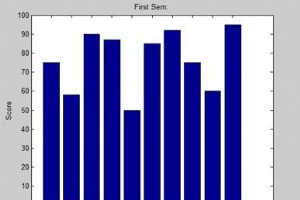
この章では、MATLAB のプロット機能とグラフィックス機能の探索を続けます。議論します− 棒グラフの描画 輪郭を描く 三次元プロット 棒グラフの描画 バー コマンドは、2 次元の棒グラフを描画します。アイデアを示すために例を挙げてみましょう. 例 10 人の生徒がいる架空の教室を考えてみましょう。これらの学生が取得した点数の割合は、75、58、90、87、50、85、92、75、60、および 95 であることがわかっています。このデータの棒グラフを描画します。 スクリプト ファイルを作成し、次のコードを入力します − x = [1:10]; y = [75, 58, 90, 87
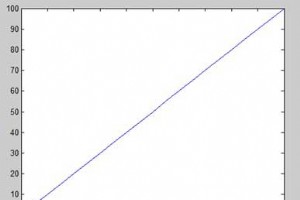
関数のグラフをプロットするには、次の手順を実行する必要があります − x を定義する 、値の範囲を指定して 変数 x について 、関数がプロットされる 関数 y =f(x) を定義します プロットを呼び出す コマンド、plot(x, y) として 次の例は、概念を示しています。単純な関数 y =x をプロットしてみましょう x の値の範囲は 0 から 100 で、増分は 5 です。 スクリプト ファイルを作成し、次のコードを入力します − x = [0:5:100]; y = x; plot(x, y) ファイルを実行すると、MATLAB は次のプロットを表

MATLAB でのデータのエクスポート (または出力) は、ファイルに書き込むことを意味します。 MATLAB では、ASCII ファイルを読み取る別のアプリケーションでデータを使用できます。このために、MATLAB にはいくつかのデータ エクスポート オプションが用意されています。 次のタイプのファイルを作成できます − 配列からの長方形の区切られた ASCII データ ファイル。 キーストロークとその結果のテキスト出力のダイアリー (またはログ) ファイル。 fprintf などの低レベル関数を使用する特殊な ASCII ファイル。 特定のテキスト ファイル形式に

MATLAB でのデータのインポートは、外部ファイルからのデータの読み込みを意味します。 インポートデータ 関数を使用すると、さまざまな形式のさまざまなデータ ファイルを読み込むことができます。次の 5 つの形式があります − Sr.No. 機能と説明 1 A =importdata(ファイル名) filename で示されるファイルから配列 A にデータをロードします。 . 2 A =importdata(-pastespecial) ファイルからではなく、システム クリップボードからデータを読み込みます。 3 A =importdata(___, delimi

関数は、一緒にタスクを実行するステートメントのグループです。 MATLAB では、関数は別のファイルで定義されます。ファイルと関数の名前は同じでなければなりません。 関数は、ローカル ワークスペース

文字列の作成は、MATLAB では非常に簡単です。実際、私たちは何度もそれを使用しています。たとえば、コマンド プロンプトで次のように入力します − ライブデモ my_string = Tutorials Point MATLAB は上記のステートメントを実行し、次の結果を返します − my_string = Tutorials Point MATLAB はすべての変数を配列と見なし、文字列は文字配列と見なします。 whos を使用しましょう 上記で作成した変数を確認するコマンド − whos MATLAB は上記のステートメントを実行し、次の結果を返します − Name

MATLAB は、符号付きおよび符号なしの整数、単精度および倍精度の浮動小数点数を含むさまざまな数値クラスをサポートしています。既定では、MATLAB はすべての数値を倍精度浮動小数点数として格納します。 任意の数値または数値の配列を整数または単精度数値として格納することを選択できます。 すべての数値型は、基本的な配列演算と数学演算をサポートしています。 さまざまな数値データ型への変換 MATLAB は、さまざまな数値データ型に変換する次の関数を提供します − 機能 目的 ダブル 倍精度数に変換 シングル 単精度数に変換 int8 8 ビット符号付き整数に変換 int16 1

コロン(:) MATLAB で最も便利な演算子の 1 つです。ベクトル、添字配列の作成、および反復の指定に使用されます . 1 から 10 までの整数を含む行ベクトルを作成する場合は、次のように記述します − ライブデモ 1:10 MATLAB はステートメントを実行し、1 から 10 までの整数を含む行ベクトルを返します − ans =

MATLAB のすべてのデータ型の変数はすべて多次元配列です。ベクトルは 1 次元配列で、マトリックスは 2 次元配列です。 ベクトルと行列についてはすでに説明しました。この章では、多次元配列について説明します。ただし、その前に、いくつかの特別なタイプの配列について説明しましょう。 MATLAB の特別な配列 このセクションでは、いくつかの特別な配列を作成するいくつかの関数について説明します。これらすべての関数で、1 つの引数は正方形の配列を作成し、2 つの引数は長方形の配列を作成します。 zeros() 関数はすべてゼロの配列を作成します − たとえば- ライブデモ zeros(5

行列は、数値の 2 次元配列です。 MATLAB では、各行にコンマまたはスペースで区切られた数字として要素を入力し、セミコロンを使用して各行の終わりをマークすることにより、行列を作成します。 たとえば、4 行 5 列の行列 a を作成してみましょう。 − ライブデモ a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] MATLAB は上記のステートメントを実行し、次の結果を返します − a = 1 2 3 4 5 2 3 4 5 6

ベクトルは、数値の 1 次元配列です。 MATLAB では 2 種類のベクトルを作成できます − 行ベクトル 列ベクトル 行ベクトル 行ベクトル 要素のセットを角括弧で囲み、スペースまたはコンマを使用して要素を区切ることによって作成されます。 ライブデモ r = [7 8 9 10 11] MATLAB は上記のステートメントを実行し、次の結果を返します − r = 7 8 9 10 11 列ベクトル 列ベクトル 要素のセットを角括弧で囲み、セミコロンを使用して要素を区切ることによって作成されます。 ライブデモ c = [7; 8; 9;
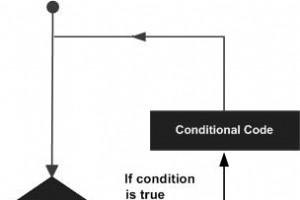
コードのブロックを数回実行する必要がある場合があります。一般に、ステートメントは順次実行されます。関数内の最初のステートメントが最初に実行され、次に 2 番目のステートメントが実行されます。 プログラミング言語は、より複雑な実行パスを可能にするさまざまな制御構造を提供します。 ループステートメントを使用すると、ステートメントまたはステートメントのグループを複数回実行できます。以下は、ほとんどのプログラミング言語でのループステートメントの一般的な形式です- MATLAB は、ループ要件を処理するために次のタイプのループを提供します。以下のリンクをクリックして詳細を確認してください − S
MATLAB