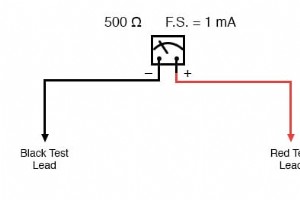
電流計は電流を測定します 電流を測定するために設計されたメーターは、測定単位が「アンペア」であるため、一般に「電流計」と呼ばれます。 電流計の設計では、動作の使用可能範囲を拡張するために追加された外部抵抗が並列で接続されます。 電圧計の場合のように直列ではなく、動きで。これは、測定された電圧ではなく、測定された電流を運動に分流させたいためであり、分流の法則回路は常に並列抵抗によって形成されているためです。 電流計の設計 電圧計の例と同じメーターの動きをとると、それ自体で非常に限定された計測器が作成され、フルスケールのたわみがわずか1mAで発生することがわかります。 メータームーブメント

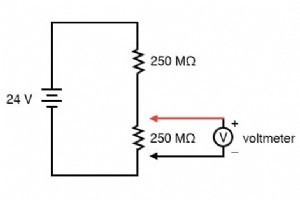
すべてのメーターは、測定している回路にある程度影響を与えます。タイヤ空気圧ゲージが、ゲージを操作するために空気が放出されると、測定されたタイヤ空気圧がわずかに変化するのと同じです。ある程度の影響は避けられませんが、適切なメーター設計によって最小限に抑えることができます。 分圧回路 電圧計は常にテスト対象のコンポーネントと並列に接続されているため、電圧計を流れる電流はテスト対象の回路の全体的な電流に寄与し、測定される電圧に影響を与える可能性があります。完全な電圧計は無限の抵抗を持っているので、テスト中の回路から電流を引き込むことはありません。ただし、完璧な電圧計は教科書のページにのみ存在し、実

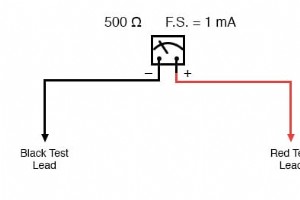
前に述べたように、ほとんどのメーターの動きは敏感なデバイスです。一部のダーソンバルムーブメントのフルスケール偏向電流定格はわずか50µAで、（内部）ワイヤ抵抗は1000Ω未満です。これにより、フルスケール定格がわずか50ミリボルト（50 µAX1000Ω）の電圧計になります。このような敏感な動きから実用的な（より高い電圧の）スケールを備えた電圧計を構築するには、測定された電圧量を動きが処理できるレベルまで下げる方法を見つける必要があります。 ダルソンバル運動計 フルスケールのたわみ定格が1mA、コイル抵抗が500ΩのD’Arsonvalメータームーブメントの問題例を始めましょう： オ

メーター 人間が読み取り可能な形式で電気量を正確に検出して表示するように構築されたデバイスです。通常、この「読み取り可能な形式」は視覚的です。つまり、目盛り上のポインターの動き、「棒グラフ」を形成するように配置された一連のライト、または数字で構成されるある種の表示です。回路の分析とテストでは、電圧、電流、抵抗の基本量を正確に測定するように設計されたメーターがあります。他にも多くの種類のメーターがありますが、この章では主に基本的な3つのメーターの設計と操作について説明します。 最新のメーターのほとんどは、設計が「デジタル」です。つまり、読み取り可能な表示は数字の形式です。古い設計のメーターは本

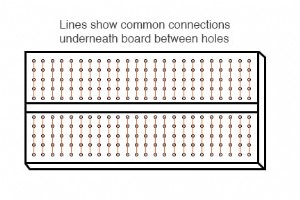
繰り返しになりますが、バッテリー/抵抗回路を構築するとき、学生または趣味の人はいくつかの異なる構築モードに直面します。おそらく最も人気のあるのは、ソルダーレスブレッドボードです。 ：相互接続されたポイントのグリッドにコンポーネントとワイヤを接続することにより、一時的な回路を構築するためのプラットフォーム。 ブレッドボードは、何百もの小さな穴が開いたプラスチックのフレームに過ぎないように見えます。ただし、各穴の下には、他の穴の下にある他のスプリングクリップに接続するスプリングクリップがあります。穴間の接続パターンは単純で均一です： シリーズ-無はんだブレッドボードでの並列回路構築 ブレ

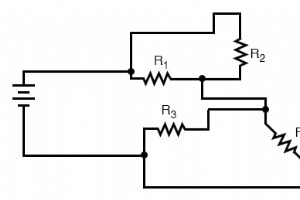
「次の場合に方程式を理解していると思います実際に解くことなく、その解の特性を予測することができます。」 —P.A.Mディラック、物理学者 ディラックからのその引用には多くの真実があります。少し変更を加えるだけで、「実際に計算を行わなくても、回路に加えられたさまざまな変更のおおよその影響を予測できれば、回路を理解できたと思います」と言うことで、彼の知恵を電気回路にまで広げることができます。 直列および並列回路の章の最後で、回路を定性的で分析する方法について簡単に検討しました。 定量的ではなく マナー。このスキルを身に付けることは、電気回路の熟練したトラブルシューティングを行うための重要な

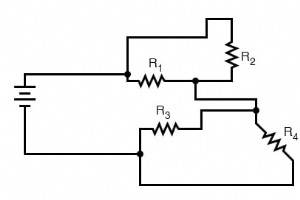
通常、複雑な回路は、私たちが従うべき、すっきりとしたきれいな回路図に配置されていません。それらは、どのコンポーネントが直列で、どのコンポーネントが互いに並列であるかを追跡するのが困難になるような方法で描画されることがよくあります。このセクションの目的は、回路図をきちんと整然と再描画するのに役立つ方法を示すことです。直並列の直並列回路を解くためのステージ削減戦略と同様に、これは説明するよりも簡単に実証できる方法です。 複雑な回路図の分析と簡略化 次の（複雑な）回路図から始めましょう。おそらく、この図は元々、技術者またはエンジニアによってこのように描かれたものです。おそらく、誰かが実際の回路の配

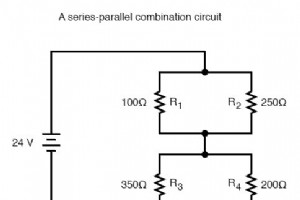
直列-並列直並列回路解析のガイドライン 直並列抵抗回路解析の目標は、回路内のすべての電圧降下、電流、および電力損失を決定できるようにすることです。この目標を達成するための一般的な戦略は次のとおりです。 ステップ1： 回路内のどの抵抗器が単純な直列または単純な並列で一緒に接続されているかを評価します。 ステップ2： 回路を再描画し、手順1で特定した直列または並列の各抵抗の組み合わせを単一の等価値の抵抗に置き換えます。テーブルを使用して変数を管理する場合は、同等の抵抗ごとに新しいテーブル列を作成します。 ステップ3： 回路全体が1つの同等の抵抗に減少するまで、手順1と2を繰り返します。

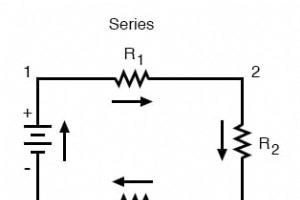
単純な直列回路では、すべてのコンポーネントがエンドツーエンドで接続され、電流が回路を流れるための1つのパスのみを形成します。 単純な並列回路では、すべてのコンポーネントが同じ2セットの電気的に共通のポイント間に接続され、バッテリーの一方の端からもう一方の端に電流が流れるための複数のパスが作成されます。 直列および並列回路に関する規則 これらの2つの基本的な回路構成のそれぞれに、電圧、電流、および抵抗の関係を説明する特定のルールセットがあります。 直列回路： 電圧降下により、合計電圧が等しくなります。 すべてのコンポーネントは同じ（等しい）電流を共有します。 抵抗は、等しい

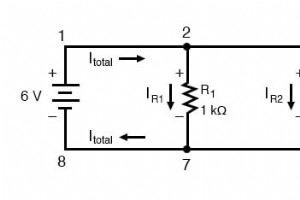
キルヒホッフの現行法とは何ですか？ キルヒホッフの現在の法則は、しばしばKCLと短縮され、「ノードに出入りするすべての電流の代数和はゼロに等しくなければならない」と述べています。 この法則は、電荷がワイヤのワイヤ接合点またはノードからどのように出入りするかを説明するために使用されます。 この情報を武器に、実際の法律の例、それが重要である理由、およびそれがどのように導き出されたかを見てみましょう。 並列回路レビュー 最後の並列回路例を詳しく見てみましょう： この回路の電圧と電流のすべての値を解く： この時点で、各分岐電流の値と回路の合計電流の値がわかります。並列回路の合計

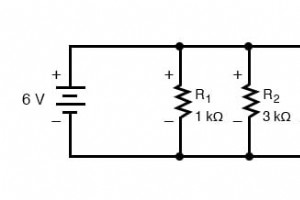
並列回路は、分流の法則と呼ばれることがよくあります。 総電流を小数部分に比例化または分割する能力のため。 これが何を意味するのかを理解するために、最初に単純な並列回路を分析して、個々の抵抗を流れる分岐電流を決定しましょう 並列回路のすべてのコンポーネントの電圧が同じであることを知っているので、電圧/電流/抵抗の表に一番上の行の電圧を6ボルトで記入できます。 オームの法則（I =E / R）を使用して、各分岐電流を計算できます。 分岐電流が並列回路で合計されて合計電流に等しくなることがわかっているので、6 mA、2 mA、および3mAを合計することで合計電流に到達できま

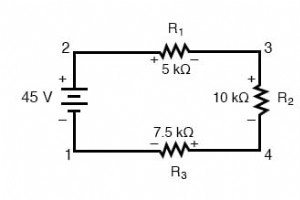
キルヒホッフの電圧法則（KVL）とは何ですか？ キルヒホッフの電圧法則として知られる原理 （1847年にドイツの物理学者Gustav R. Kirchhoffによって発見された）は次のように述べることができます： 「ループ内のすべての電圧の代数和はゼロに等しくなければなりません」 代数 、私は符号（極性）と大きさを説明することを意味します。 ループ 、つまり、回路内のあるポイントからその回路内の他のポイントまでトレースされ、最終的に最初のポイントに戻るパスを意味します。 直列回路におけるキルヒホッフの電圧法則のデモンストレーション 直列回路の例をもう一度見てみましょう。今回は、電

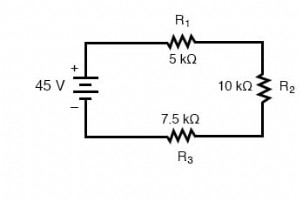
簡単な直列回路を分析して、個々の抵抗器の両端の電圧降下を決定しましょう。 与えられた個々の抵抗の値から、抵抗が直列に追加されることを知って、回路全体の抵抗を決定できます。 総回路抵抗を決定する ここから、オームの法則（I =E / R）を使用して、総電流を決定できます。これは、各抵抗器の電流と同じであり、直列回路のすべての部分で電流が等しくなります。 オームの法則を使用して電流を計算する これで、回路電流が2 mAであることがわかったので、オームの法則（E =IR）を使用して、各抵抗の両端の電圧を計算できます。 電流がすべての抵抗器で同じであることを考える

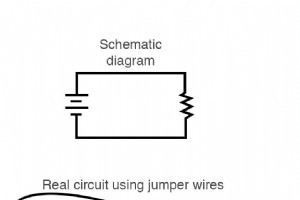
電気について学ぶ過程で、抵抗器と電池を使って独自の回路を構築したいと思うでしょう。この回路アセンブリの問題では、いくつかのオプションが利用可能ですが、他のオプションよりも簡単なものもあります。このセクションでは、この章に示されている回路だけでなく、より高度な回路を構築するのに役立ついくつかの製造技術について説明します。 回路構築のためのワニ口クリップジャンパー線の使用 構築したいのが単純な単一バッテリー、単一抵抗回路だけである場合、ワニ口クリップを簡単に使用できます。 このようなジャンパー線： 両端に「ワニ」スタイルのスプリングクリップが付いたジャンパー線は、コンポーネントを

技術者の仕事は、誤動作している回路の「トラブルシューティング」（問題の特定と修正）を伴うことがよくあります。優れたトラブルシューティングは、要求が厳しくやりがいのある作業であり、基本的な概念の完全な理解、仮説を立てる能力（効果の提案された説明）、確率に基づいてさまざまな仮説の価値を判断する能力（1つの特定の原因の可能性）が必要です。別のものよりも優れている可能性があります）、そして問題を修正するための解決策を適用する際の創造性の感覚。 これらのスキルを科学的方法論に抽出することは可能ですが、ほとんどの実践的なトラブルシューティング担当者は、トラブルシューティングにはちょっとした芸術が含まれ、

オームの法則を使用する際の注意事項 エレクトロニクスの学生がオームの法則を適用する際に犯す最も一般的な間違いの1つは、電圧、電流、抵抗のコンテキストを混合することです。言い換えると、学生は、1つの抵抗器を通るI（電流）の値と、相互接続された抵抗器のセット全体のE（電圧）の値を誤って使用して、その1つの抵抗器の抵抗に到達すると考えている可能性があります。 そうではありません！この重要なルールを覚えておいてください。オームの法則の方程式で使用される変数は、共通でなければなりません。 検討中の回路の同じ2つのポイントに。私はこのルールを強調しすぎることはできません。これは、近くのコンポーネントの

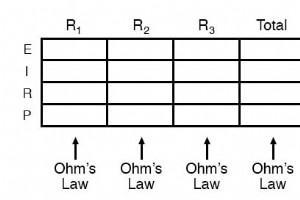
抵抗性コンポーネントの消費電力を計算するときは、3つの電力方程式のいずれかを使用して、各コンポーネントに関連する電圧、電流、および/または抵抗の値から答えを導き出します。 これは、電圧、電流、抵抗の使い慣れたテーブルに別の行を追加することで簡単に管理できます。 特定のテーブル列の検出力は、適切なオームの法則の方程式（適切な）によって求めることができます。 その列のE、I、およびRにどのような数字が存在するかに基づいています。 総電力と個別電力の興味深いルールは、すべてに対して加算的であるということです。 回路の構成：直列、並列、直列/並列、またはその他。電力は仕事率の尺度であ

学生が最初に並列抵抗方程式を見るとき、尋ねるべき自然な質問は、「それはどこで 何から来たの？」それは本当に奇妙な算術であり、その起源は良い説明に値します。 抵抗とコンダクタンスの違いは何ですか？ 抵抗は、定義上、摩擦の尺度です。 コンポーネントは、それを通る電流の流れに現れます。抵抗は大文字の「R」で表され、「オーム」の単位で測定されます。ただし、この電気的特性は、その逆の観点から考えることもできます。簡単 難しいのではなく、電流がコンポーネントを流れるためです。 。 抵抗の場合 は、電流が流れるのがどれほど難しいかを表すために使用する言葉です。次に、電流が流れるのがどれほど簡単かを表す

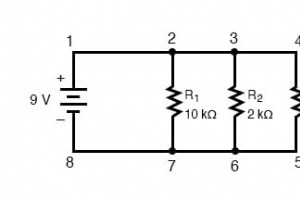
このページでは、並列回路に関して理解しておくべき3つの原則の概要を説明します。 電圧： 電圧は、並列回路のすべてのコンポーネントで等しくなります。 現在： 合計回路電流は、個々の分岐電流の合計に等しくなります。 抵抗： 個々の抵抗は減少する 追加ではなく、より小さな総抵抗に等しくする 合計を計算します。 これらの原理を示す並列回路の例をいくつか見てみましょう。 まず、3つの抵抗と1つのバッテリーで構成される並列回路から始めます。 並列回路の電圧 並列回路について理解するための最初の原則は、電圧が回路内のすべてのコンポーネントで等しいということです。 。これは、並列回路には

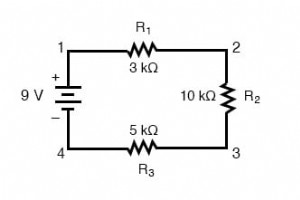
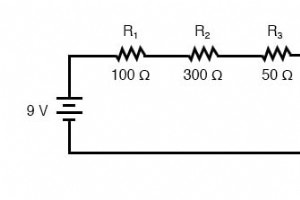
このページでは、直列回路に関して理解しておくべき3つの原則の概要を説明します。 現在 ：電流の量は、直列回路のどのコンポーネントでも同じです。 抵抗 ：直列回路の合計抵抗は、個々の抵抗の合計に等しくなります。 電圧 ：直列回路の供給電圧は、個々の電圧降下の合計に等しくなります。 これらの原理を示す直列回路の例をいくつか見てみましょう。 まず、3つの抵抗と1つのバッテリーで構成される直列回路から始めます。 直列回路について理解するための最初の原則は次のとおりです。 直列回路の電流量は、回路内のどのコンポーネントでも同じです。 これは、直列回路に電流が流れる経