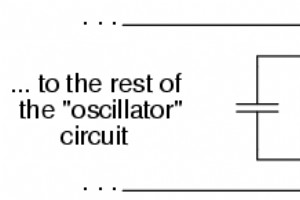
これまでのところ、共振の現象は役に立たない好奇心であるか、せいぜい避けるべき厄介なものであるように思われます（特に、直列共振によってAC電圧源の両端が短絡する場合）。ただし、そうではありません。共振は、さまざまなアプリケーションで使用される無効AC回路の非常に貴重な特性です。共振の用途の1つは、AC信号を生成するように設計された回路で安定した周波数の条件を確立することです。通常、この目的のために並列（タンク）回路が使用され、コンデンサとインダクタが直接接続され、相互にエネルギーを交換します。振り子を使用して時計機構の振動の周波数を安定させることができるのと同様に、タンク回路を使用してAC発振器

同様の効果は、直列の誘導/容量性回路でも発生します。共振状態に達すると（容量性リアクタンスと誘導性リアクタンスが等しい）、2つのインピーダンスが互いに打ち消し合い、合計インピーダンスがゼロになります。 例： 単純な直列共振回路。 159.155 Hzの共振周波数で合計直列インピーダンスが0Ωに等しい場合、結果は短絡になります。 共振時にAC電源の両端。上に描いた回路では、これは良くありません。 コンデンサとインダクタに直列に小さな抵抗（下の図）を追加して、最大回路電流をいくらか制限し、同じ周波数範囲で別のSPICE分析を実行します。 SPICEに

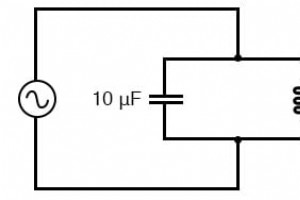
タンク回路の共振 コンデンサとインダクタのリアクタンスが互いに等しい場合、タンク回路で共振状態が発生します。誘導性リアクタンスは周波数の増加とともに増加し、容量性リアクタンスは周波数の増加とともに減少するため、これら2つのリアクタンスが等しくなる周波数は1つだけになります。例： 単純な並列共振回路（タンク回路）。 上記の回路には、10 µFのコンデンサと100mHのインダクタがあります。与えられた周波数でそれぞれのリアクタンスを決定するための方程式がわかっていて、2つのリアクタンスが互いに等しい点を探しているので、2つのリアクタンスの式を互いに等しく設定し、代数的に周波数

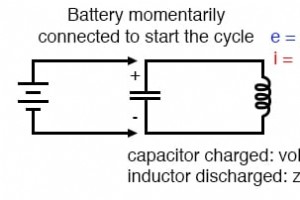
コンデンサは、電界の形でエネルギーを蓄積し、蓄積されたエネルギーを電位として電気的に示します：静電圧 。インダクタは、磁場の形でエネルギーを蓄積し、蓄積されたエネルギーを電子の運動運動として電気的に示します。電流 。 コンデンサとインダクタは同じリアクティブコインの裏側であり、相補モードでエネルギーを蓄積および放出します。これらの2種類の反応性成分が直接接続されている場合、エネルギーを蓄えるそれらの補完的な傾向は異常な結果を生み出します。 コンデンサまたはインダクタのいずれかが充電状態で起動すると、2つのコンポーネントがそれらの間でエネルギーを交換し、独自のAC電圧および電流サイクルを作成

電力（P）の計算を除いて、すべてのAC回路の計算は、DC回路の計算と同じ一般原則に基づいています。唯一の重要な違いは、AC計算では複雑な量が使用されるのに対し、DC計算ではスカラー量が使用されるという事実です。 オームの法則、キルヒホッフの法則、そしてDCで学習したネットワーク定理でさえ、電圧、電流、インピーダンスがすべて複素数で表されている場合、ACにも当てはまります。 DC回路に適用されるのと同じトラブルシューティング戦略がACにも当てはまりますが、ACは、ハンドヘルドマルチメータによって登録されない位相角のために操作がより困難になる可能性があります。 パワー は完全に別の主題であり

コンダクタンスとは何ですか？ DC回路の研究では、電気の学生は抵抗の反対を意味する用語に出くわします：コンダクタンス 。これは、並列抵抗の数式を調べるときに役立つ用語です。R parallel =1 /（1 / R 1 + 1 / R 2 +。 。 。 1 / R n 。 より多くの並列コンポーネントが回路に含まれるにつれて減少する抵抗とは異なり、コンダクタンスは単純に追加されます。数学的には、コンダクタンスは抵抗の逆数であり、「並列抵抗式」の各1 / R項は実際にはコンダクタンスです。 「抵抗」という用語は、回路内を流れる電子に対する反対の量を表しますが、「コンダクタンス

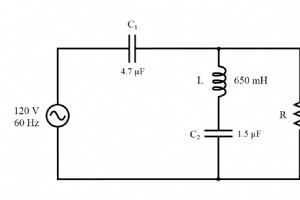
直列および並列AC回路解析がDC回路解析と基本的に異ならないことを確認したので、スカラーの代わりに複素数を使用して表すだけで、直並列解析も同じになるのは当然のことです。電圧、電流、およびインピーダンス。この直並列回路を例にとってみましょう： 直列-並列R、L、C回路の例。 いつものように、最初の仕事は、AC電源の周波数に基づいてすべてのコンポーネントのインピーダンス（Z）の値を決定することです。これを行うには、最初にすべてのインダクタとコンデンサのリアクタンス（X）の値を決定し、次にリアクタンス（X）と抵抗（R）の数値を適切なインピーダンス（Z）の形式に変換する必要がありま

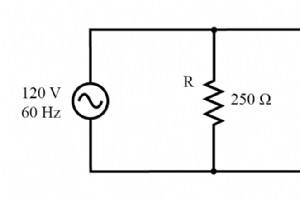
直列回路から同じコンポーネントを取り出し、それらを並列構成に再配置して、簡単な回路例を示すことができます。 R、L、Cの並列回路の例。 並列コンポーネントのインピーダンス これらのコンポーネントが直列ではなく並列に接続されているという事実は、個々のインピーダンスにまったく影響を与えません。電源が以前と同じ周波数である限り、誘導性および容量性リアクタンスはまったく変化しません。 インピーダンスがコンポーネント値を置き換えるR、L、およびC並列回路の例。 すべてのコンポーネント値をインピーダンス（Z）で表すと、分析テーブルを設定して、最後の問題例のように進

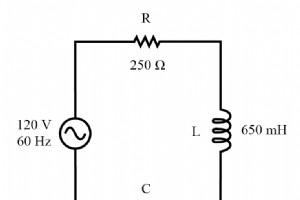
次の回路例を見て分析してみましょう。 シリーズR、L、C回路の例。 リアクタンスの解決 最初のステップは、インダクタとコンデンサのリアクタンス（オーム）を決定することです。 次のステップは、すべての抵抗とリアクタンスを数学的に一般的な形式で表現することです：インピーダンス。 （下の図） 誘導性リアクタンスは正の虚数インピーダンス（または+ 90°のインピーダンス）に変換され、容量性リアクタンスは負の虚数インピーダンス（-90°のインピーダンス）に変換されることに注意してください。もちろん、抵抗は依然として純粋に「実際の」インピーダンス（極角0°）と見なされ

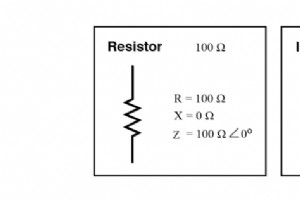
同じAC回路に接続された抵抗、インダクタ、コンデンサの効果を調べる前に、いくつかの基本的な用語と事実を簡単に確認しましょう。 抵抗 これは本質的に摩擦です 電流の流れに対して。すべてのコンダクターにある程度存在します（スーパーを除く） 導体！）、特に抵抗器で。交流電流が抵抗を通過すると、電流と同相の電圧降下が発生します。抵抗は数学的に「R」の文字で表され、オーム（Ω）の単位で測定されます。 リアクタンス これは本質的に慣性です 電流の流れに対して。これは、印加された電圧または電流にそれぞれ比例して電界または磁界が発生する場所に存在します。しかし、最も顕著なのはコンデンサとインダクタです。

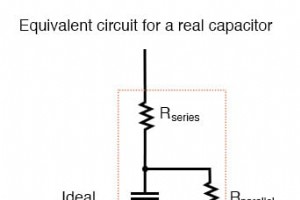
インダクタと同様に、理想的なコンデンサは純粋にリアクティブなデバイスであり、抵抗性（電力損失）効果はまったくありません。もちろん、現実の世界では、これほど完璧なものはありません。ただし、コンデンサには、一般的により純粋であるという利点があります。 インダクタよりも無効なコンポーネント。 インダクタを使用するよりも、内部直列抵抗が低いコンデンサを設計および構築する方がはるかに簡単です。これの実際的な結果は、実際のコンデンサは通常、インダクタよりも90°（実際には-90°）に近いインピーダンス位相角を持っているということです。 その結果、同等のインダクタよりも消費電力が少なくなる傾向があります

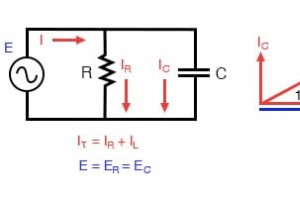
直列の回路例で同じ値のコンポーネントを使用して、それらを並列に接続し、何が起こるかを確認します。 並列R-C回路。 並列の抵抗とコンデンサ 電源は直列の回路例と同じ周波数であり、抵抗とコンデンサは両方とも同じ値の抵抗と静電容量を持っているため、それらも同じ値のインピーダンスを持っている必要があります。したがって、同じ「指定された」値で分析テーブルを開始できます。 これは並列回路であるため、電圧はすべてのコンポーネントで均等に共有されることがわかっているため、すべての列に合計電圧（10ボルト∠0°）の数値を配置できます。 オームの法則を使用した計

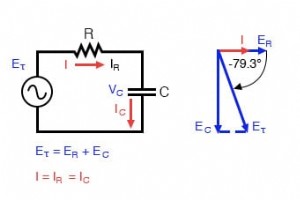
前のセクションでは、単純な抵抗のみおよびコンデンサのみのAC回路で何が起こるかを学びました。次に、2つのコンポーネントを直列に組み合わせて、効果を調査します。 直列コンデンサ回路：電圧は電流を0°から90°遅らせます。 インピーダンス計算 抵抗は周波数に関係なくAC電流に対して5Ωの抵抗を提供し、コンデンサは60HzでAC電流に対して26.5258Ωのリアクタンスを提供します。 抵抗器の抵抗は実数（5Ω∠0°、または5 +j0Ω）であり、コンデンサのリアクタンスは虚数（26.5258Ω∠-90°、または0-j26.5258Ω）であるため、複合効果2つの成分のうち、2つの数

コンデンサ対抵抗器 コンデンサは抵抗と同じようには動作しません。抵抗器は電圧降下に正比例して電子の流れを許容しますが、コンデンサは変化に対抗します。 新しい電圧レベルまで充電または放電するときに電流を引き込むか供給することにより、電圧を下げます。 コンデンサを「通過する」電子の流れは、変化率に正比例します。 コンデンサの両端の電圧の。電圧変化に対するこの反対は、リアクタンスの別の形式です。 、しかしインダクタによって示される種類とは正反対のものです。 コンデンサ回路の特性 数学的に表現すると、コンデンサを「流れる」電流とコンデンサ両端の電圧変化率の関係は次のようになります。

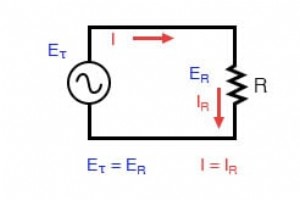
純粋な抵抗膜方式AC回路：電圧と電流は同相です。 ソースと抵抗で構成される非常に単純なAC回路の電流と電圧をプロットすると（上の図）、次のようになります:(下の図） 抵抗回路の「同相」の電圧と電流。 抵抗器は、すべての期間で抵抗器の両端の電圧に正比例する量の電流を許容するため、電流の波形は電圧の波形と正確に同相です。 プロットの横軸に沿った任意の時点を見て、それらの電流と電圧の値を相互に比較できます（波の値を「スナップショット」で見ると、瞬時値 、そのインスタントでの値を意味します 時間内に）。 電圧の瞬時値がゼロの場合、抵抗を流れる瞬時電流もゼロになります。同

電気工学における銅の表皮深さ 前述のように、表皮効果は、交流電流が固体導体の中心を通過するのを避け、表面近くの伝導に制限される傾向がある場合です。 これにより、交流電子流を運ぶために利用できる導体の断面積が効果的に制限され、その導体の抵抗が通常の直流の抵抗よりも大きくなります。 表皮効果：表皮効果は、頻度が高くなるにつれて減少します。 使用中のすべての断面積を持つ導体の電気抵抗は、「DC抵抗」として知られています。同じ導体の「AC抵抗」は、表皮効果に起因するより高い数値を指します。 ご覧のとおり、高周波では、AC電流が導体の断面積の大部分を通過することを回避します。電

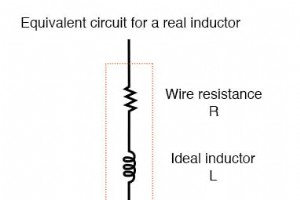
理想的なケースでは、インダクタは純粋にリアクティブなデバイスとして機能します。つまり、AC電流に対する反対は、抵抗性コンポーネントの場合のように電子摩擦ではなく、電流の変化に対する誘導反応に厳密に基づいています。 ただし、インダクタのリアクティブ動作はそれほど純粋ではありません。そもそも、それらはワイヤーでできており、すべてのワイヤーがある程度の抵抗を持っていることを私たちは知っています（超電導ワイヤーでない限り）。 この内蔵抵抗は、次のように、コイルの完全なインダクタンスと直列に接続されているかのように機能します。 インダクタ実際のインダクタの等価回路。 したがって、

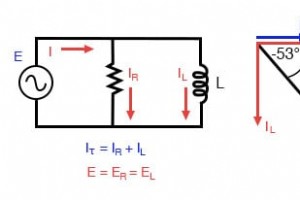
直列の回路例と同じコンポーネントを使用して、それらを並列に接続してみましょう。 並列R-L回路。 電源は直列の回路例と同じ周波数を持ち、抵抗とインダクタはそれぞれ同じ値の抵抗とインダクタンスを持っているため、それらも同じ値のインピーダンスを持っている必要があります。したがって、同じ「指定された」値で分析テーブルを開始できます。 今回の分析手法の唯一の違いは、直列回路の規則ではなく、並列回路の規則を適用することです。アプローチは基本的にDCの場合と同じです。電圧は並列回路内のすべてのコンポーネントで均一に共有されることがわかっているため、合計電圧（10ボルト∠

前のセクションでは、単純な抵抗のみおよびインダクタのみのAC回路で何が起こるかを調べました。次に、2つのコンポーネントを直列に混合し、効果を調査します。 直列抵抗インダクタ回路の例 使用する例としてこの回路を取り上げます： 直列抵抗インダクタ回路：電流は印加電圧より0oから90o遅れます。 抵抗は周波数に関係なくAC電流に対して5Ωの抵抗を提供し、インダクタは60HzでAC電流に対して3.7699Ωのリアクタンスを提供します。 抵抗器の抵抗は実数（5Ω∠0°、または5 +j0Ω）であり、インダクタのリアクタンスは虚数（3.7699Ω∠90°、または0 +j3.7699Ω

抵抗とインダクタ インダクタは抵抗と同じようには動作しません。抵抗器は（電流に正比例する電圧を下げることによって）抵抗器を流れる電流に対抗するだけですが、インダクターは変化に対抗します。 変化率に正比例する電圧を下げることにより、それらを流れる電流を 電流の。 レンツの法則に準拠 、この誘導電圧は常に電流を現在の値に維持しようとするような極性です。つまり、電流の大きさが増加している場合、誘導電圧は電流の流れを「押し」ます。電流が減少している場合、極性が反転し、電流を「押して」減少に対抗します。 現在の変化に対するこの反対は、リアクタンスと呼ばれます。 、抵抗ではなく。数学的に表現すると、