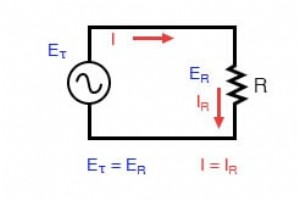
AC回路の瞬時値 純粋な抵抗AC回路：抵抗の電圧と電流は同相です。 ソースと抵抗で構成される非常に単純なAC回路の電流と電圧をプロットすると（上の図）、次のようになります:(下の図） 抵抗回路の「同相」の電圧と電流。 抵抗器はすべての時間で電流の流れに単純かつ直接抵抗するため、抵抗器の両端の電圧降下の波形は、抵抗器を流れる電流の波形と正確に同相です。 プロットの横軸に沿った任意の時点を見て、それらの電流と電圧の値を相互に比較できます（波の値を「スナップショット」で見ると、瞬時値 、そのインスタントでの値を意味します 時間内に）。 電流の瞬時値がゼロの場合

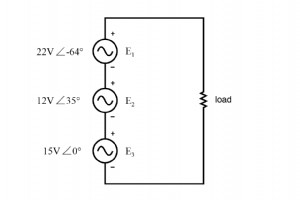
3つのAC電圧源を直列に接続し、複素数を使用して付加電圧を決定しましょう。 DC回路の研究で学んだすべての規則と法則は、電力計算（ジュールの法則）を除いて、AC回路にも適用されます（オームの法則、キルヒホッフの法則、ネットワーク分析方法）。 唯一の条件は、すべての変数が必要であるということです。 位相と大きさを考慮して複雑な形で表現され、すべての電圧と電流は同じ周波数でなければなりません（それらの位相関係が一定に保たれるため）。 （下の図） KVLを使用すると、複雑な電圧を追加できます。 3つの電圧源すべての極性マークは、負荷抵抗の両端の合計電圧を作成するために、指定

複素数は、電圧や電流などのAC量間の位相シフトを象徴的に示す便利な方法を提供するため、AC回路解析に役立ちます。 ただし、ほとんどの人にとって、抽象的なベクトルと実際の回路量の同等性を把握するのは簡単ではありません。この章の前半で、AC電圧源に複素数形式の電圧値（大きさおよび）がどのように与えられるかを見ました。 位相角）、および極性マーキング。 交流には直流のように「極性」が設定されていないため、これらの極性のマーキングと位相角との関係は混乱する傾向があります。このセクションは、これらの問題のいくつかを明確にすることを目的として書かれています。 電圧は本質的に相対的です 量。電圧を測定

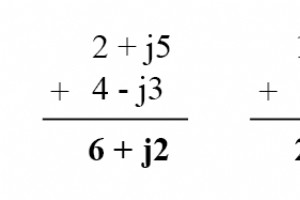
複素数はスカラー数と同じように正当な数学的実体であるため、他の種類の数と同じように、加算、減算、乗算、除算、二乗、反転などを行うことができます。 関数電卓の中には、2つ以上の複素数に対してこれらの操作を直接実行するようにプログラムされているものもありますが、これらの操作は「手動」で実行することもできます。このセクションでは、基本的な操作がどのように実行されるかを示します。 非常に 複素数に対して簡単に算術関数を実行できる関数電卓を装備することをお勧めします。これにより、すべての計算を長時間行う必要がある場合よりも、AC回路の研究がはるかに快適になります。 長方形形式の複素数の加算と減算

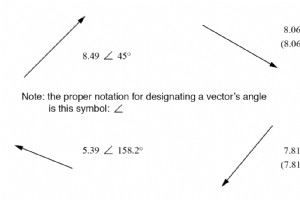
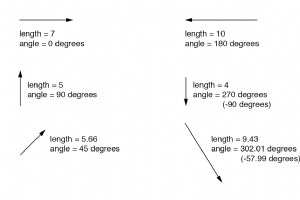
ベクトルを描画せずに複素数を処理するには、最初にある種の標準的な数学表記が必要です。複素数表記には、次の2つの基本的な形式があります。極 および長方形 。 複素数の極形式 極形式では、複素数は長さで表されます。 （別名マグニチュード 、絶対値 、またはモジュラス ）と角度 そのベクトルの（通常は次のような角度記号で示されます：∠）。 マップの例えを使用すると、ニューヨーク市からサンディエゴまでのベクトルの極座標表記は、「南西2400マイル」のようになります。ベクトルとその極性表記の2つの例を次に示します。 極性表記のベクトル。 AC回路計算でのベクトル角度の標準的な向き

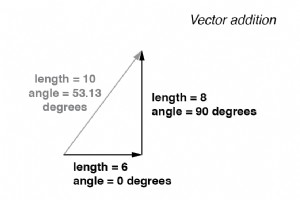
珍しい角度のベクトルを追加すると、それらの大きさ（長さ）の合計は、スカラーの大きさのベクトルとはまったく異なります:(下の図） ベクトルの大きさは、角度が等しくない場合に直接追加されません。 2つのAC電圧（90°位相がずれている）を直列に接続して加算した場合、DCのスカラー電圧のように、それらの電圧の大きさは直接加算または減算されません。 代わりに、これらの電圧量は複雑な量であり、三角法で加算される上記のベクトルと同様に、0°の6ボルトの電源を90°の8ボルトの電源に追加すると、位相角で10ボルトになります。 53.13°の:(下の図） 6Vおよび8Vソー

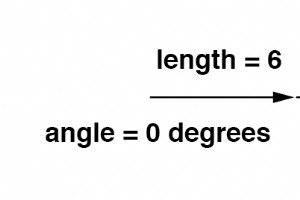
ベクトルは、数直線上の数値と同じように数学的なオブジェクトであることに注意してください。ベクトルは、加算、減算、乗算、および除算できます。加算はおそらく視覚化するのに最も簡単なベクトル演算なので、それから始めます。共通の角度を持つベクトルを追加すると、それらの大きさ（長さ）は通常のスカラー量と同じように合計されます:(下の図） 同様に、同じ位相角のAC電圧源が直列に接続されている場合、それらの電圧はDCバッテリーで予想されるように加算されます:(下の図） 2つのAC電源のリード線の横にある（+）および（-）極性マークに注意してください。 ACにはDCと同じ意味で

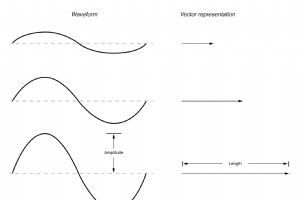
では、AC量の電圧または電流をベクトルの形でどのように正確に表すことができるでしょうか。ベクトルの長さは、次のように波形の大きさ（または振幅）を表します:(下の図） 波形の振幅が大きいほど、対応するベクトルの長さが長くなります。ただし、ベクトルの角度は、問題の波形と時間の「基準」として機能する別の波形との間の位相シフトを度単位で表します。 通常、回路内の波形の位相が表現されるとき、それは電源電圧波形（任意に「at」0°であると述べられている）を参照します。フェーズは常に相対的であることを忘れないでください 絶対特性ではなく、2つの波形間の測定。 （下の図）

2つの都市間の距離を説明する必要がある場合は、マイル、キロメートル、またはその他の線形測定単位で構成される1つの数値で構成される回答を提供できます。 ただし、ある都市から別の都市への移動方法を説明する場合、これら2つの都市間の距離だけでなく、より多くの情報を提供する必要があります。 方向に関する情報も提供する必要があります 旅行にも。 線形距離など、単一の次元を表す種類の情報は、スカラーと呼ばれます。 数学の量。スカラー数は、これまでのほとんどすべての数学アプリケーションで使用した種類の数です。 たとえば、バッテリーによって生成される電圧はスカラー量です。ワイヤーの抵抗（オーム）、または

電気のより魅力的な用途の1つは、電波と呼ばれる目に見えないエネルギーの波紋の生成です。 。交流に関するこのレッスンの範囲が限られているため、概念を完全に探求することはできません。いくつかの基本原則について説明します。 エルステッドが誤って電磁気学を発見したことで、電気と磁気が相互に関連していることがわかりました。 導体に電流を流すと、流れの軸に垂直な磁場が発生しました。同様に、導体が導体に垂直な磁束の変化にさらされた場合、その導体の長さに沿って電圧が生成されました。 これまでのところ、科学者たちは、電気と磁気が常に互いに直角に影響しているように見えることを知っていました。しかし、主要な発

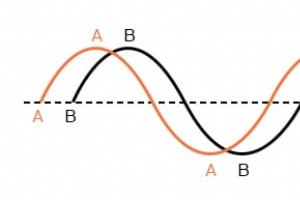
互いにずれている2つ以上のAC電圧または電流を関連付ける必要がある場合、事態は複雑になり始めます。 「脱調」とは、2つの波形が同期していないことを意味します。つまり、それらのピークとゼロ点が同じ時点で一致していません。下の図のグラフは、この例を示しています。 位相がずれた波形。 上に示した2つの波（A対B）は同じ振幅と周波数ですが、互いにずれています。技術用語では、これは位相シフトと呼ばれます 。以前、0〜360度の範囲の角度、完全な円の三角関数の正弦関数を計算することにより、「正弦波」をプロットする方法を説明しました。 正弦波の開始点は、0度で振幅がゼロで、90度で完全な正

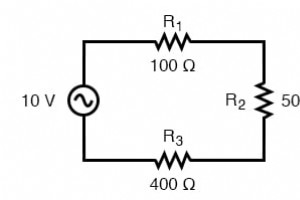
次の数章の過程で、インダクタンスと静電容量のある回路の交流の複雑な性質のために、AC回路の測定と計算が非常に複雑になる可能性があることを学びます。 ただし、AC電源と抵抗だけを含む単純な回路（下の図）では、DCの同じ法則と規則が単純かつ直接適用されます。 抵抗膜方式のAC回路の計算はDCの場合と同じです。 直列抵抗は依然として追加され、並列抵抗は依然として減少し、キルヒホッフとオームの法則は依然として当てはまります。実際、後で発見するように、これらの規則と法律は常に 確かに、電圧、電流、および電流に対する反対の量を、より高度な数学的形式で表現する必要があるだけです。

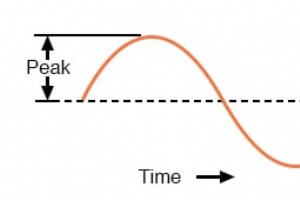
これまでのところ、AC電圧は極性が交互になり、AC電流は方向が交互になることがわかっています。また、ACはさまざまな方法で交互に変化する可能性があることもわかっています。時間の経過とともに変化を追跡することで、ACを「波形」としてプロットできます。 波が繰り返されるまでにかかる時間（「周期」）を測定することで交代率を測定し、これを単位時間あたりのサイクル数または「周波数」として表すことができます。音楽では、頻度はピッチと同じです。 、これは、ある音符を別の音符と区別するための重要なプロパティです。 しかし、AC量の大小を表現しようとすると、測定の問題が発生します。電圧と電流の量が一般的に安

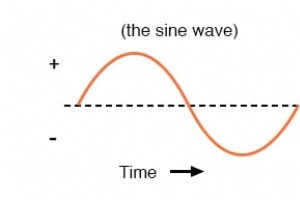
オルタネーターがAC電圧を生成すると、電圧は時間の経過とともに極性を切り替えますが、非常に特殊な方法で切り替えます。時間の経過とともにグラフ化すると、オルタネーターから極性が交互に変わるこの電圧によってトレースされる「波」は、正弦波として知られる明確な形状を取ります。 ：下の図 時間の経過に伴うAC電圧のグラフ（正弦波）。 電気機械式オルタネーターからの電圧プロットでは、一方の極性からもう一方の極性への変化は滑らかで、電圧レベルはゼロ（「クロスオーバー」）ポイントで最も急速に変化し、ピークで最もゆっくりと変化します。 0〜360度の水平範囲で「正弦」の三角関数をグラフ化

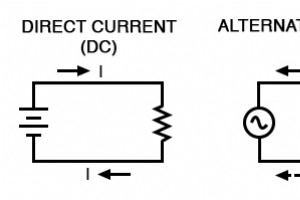
電気のほとんどの学生は、直流として知られているものから勉強を始めます。 （DC）は、一定の方向に流れる電気、および/または一定の極性の電圧を持っている電気です。 DCは、バッテリー（明確な正と負の端子を持つ）によって生成される電気の種類、または特定の種類の材料を互いにこすり合わせることによって生成される電荷​​の種類です。 交流と直流 DCは便利で理解しやすいものですが、使用されている電気の「種類」はDCだけではありません。特定の電源（特に回転式電気機械式発電機）は、自然に極性が交互に変化する電圧を生成し、時間の経過とともに正と負が反転します。 電圧スイッチングの極性として、または前後の

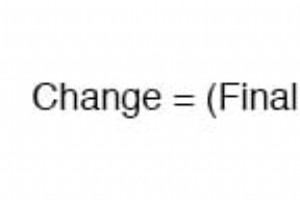
場合によっては、無効回路が所定の値に達するまでにかかる時間を決定する必要があります。これは、正確なタイミング機能を実行するようにRCまたはL / R回路を設計している場合に特に当てはまります。これを計算するには、「ユニバーサル時定数式」を変更する必要があります。元の式は次のようになります： ユニバーサル時定数を使用した時間の解決 ただし、変化量ではなく、時間で解決したいと考えています。これを行うために、時間はすべて等号の片側にあり、残りはすべて反対側にあるように、数式を代数的に操作します。 ln 時定数項のすぐ右側の指定は、自然対数です。 関数： e

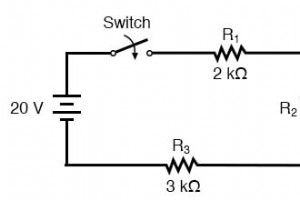
これまでに見た単純な直列構成よりも複雑な回路に遭遇した場合はどうしますか？この回路を例に取ってください： 単純な時定数の式（τ=RC）は、コンデンサに接続された単純な直列抵抗に基づいています。さらに言えば、誘導回路の時定数式（τ=L / R）も単純な直列抵抗の仮定に基づいています。では、抵抗がコンデンサ（またはインダクタ）と直並列に接続されているこのような状況で何ができるでしょうか？ テブナンの定理 その答えは、ネットワーク分析の研究から得られたものです。テブナンの定理は、すべてを減らすことができることを示しています いくつかの簡単な手順で、1つの電圧源、1つの直列抵抗、およ

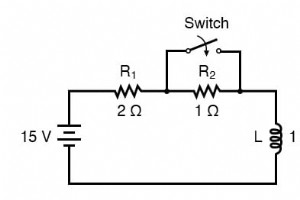
電圧と電流の開始値がそれぞれ完全に「放電」された状態ではない場合、DC無効回路を分析する必要がある場合があります。言い換えると、コンデンサはゼロボルトで開始するのではなく、部分的に充電された状態で開始する可能性があり、インダクタは、これまで想定していたゼロではなく、すでに一定量の電流で開始する可能性があります。 この回路を例にとると、スイッチが開いた状態から始まり、スイッチが閉じた位置にある状態で終わります。 これは誘導回路であるため、電流の開始値と終了値を決定することから分析を開始します。 。このステップは、誘導回路を分析するときに非常に重要です。開始電圧と終了電圧が 電

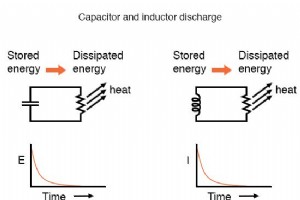
L / R時定数について学ぶ 誘導回路の時定数計算が容量性回路の時定数計算と異なる理由は、電子工学の新入生にとってしばしば困惑します。抵抗-コンデンサ回路の場合、時定数（秒単位）は、オーム単位の抵抗とファラッド単位の静電容量の積（乗算）から計算されます：τ=RC。 ただし、抵抗-インダクタ回路の場合、時定数は、オーム単位の抵抗に対するヘンリーのインダクタンスの商（除算）から計算されます：τ=L / R。 この計算の違いは、定性的に大きな影響を与えます。 過渡回路応答の分析。抵抗-コンデンサ回路は、低抵抗ではより速く応答し、高抵抗ではより遅く応答します。抵抗-インダクタ回路は正反対で、高抵

時間の経過に伴う無効DC回路の値を計算する確実な方法があります。 リアクティブDC回路の値の計算 最初のステップは、コンデンサまたはインダクタが変化に対抗する量の開始値と最終値を特定することです。つまり、反応性成分が一定に保とうとしている量が何であれ。コンデンサの場合、この量は電圧です。;インダクタの場合、この量は電流 。回路内のスイッチが閉じている（または開いている）と、リアクティブコンポーネントはその量をスイッチ遷移前と同じレベルに維持しようとするため、値は「開始」値に使用されます。 この数量の最終的な値は、無限の時間が経過した後の数量になります。これは、コンデンサが開回路であるかのよ