この章の前半のいくつかのSPICE分析で見たように、変圧器の出力電圧は、定電圧入力であっても、負荷抵抗の変化によっていくらか変化します。 変動の程度は、一次巻線と二次巻線のインダクタンスの影響を受けます。特に、巻線抵抗と一次巻線と二次巻線間の相互インダクタンス（磁気結合）の程度が含まれます。 変圧器が負荷から（理想的には）一定の電圧源と見なされる電力変圧器アプリケーションの場合、負荷電流の変動が大きい場合は、2次電圧の変動をできるだけ少なくすることをお勧めします。 電圧調整式 電力変圧器が負荷電流の範囲にわたって一定の二次電圧をどれだけうまく維持するかの尺度は、変圧器の電圧調整と呼ばれま

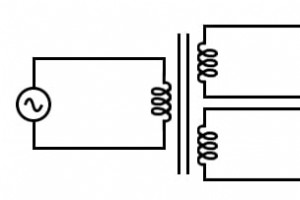
複数のセカンダリを持つトランスフォーマー 変圧器は非常に用途の広いデバイスです。相互インダクタ間のエネルギー伝達の基本概念は、単一の一次コイルと単一の二次コイルの間で十分に役立ちますが、トランスは2セットの巻線だけで作成する必要はありません。このトランス回路を考えてみましょう： 複数のセカンダリを備えたトランスは、複数の出力電圧を提供します。 ここで、3つのインダクタコイルは共通の磁気コアを共有し、それらを磁気的に「結合」または「リンク」します。相互インダクタの単一のペアで見られる巻線の巻数比と電圧比の関係は、ここでも複数のコイルのペアに当てはまります。 上記のような変

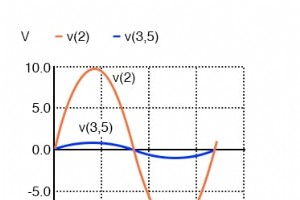
トランスは本質的にACデバイスであるため、一次回路と二次回路の間の位相関係に注意する必要があります。以前のSPICEの例を使用して、一次回路と二次回路の波形をプロットし、自分自身の位相関係を確認できます。 ナツメグで使用するスパイス過渡解析ファイル： 変成器 v1 1 0 sin（0 15 60 0 0） rbogus1 1 2 1e-12 v2 5 0 dc 250 l1 2 0 10000 l2 3 5100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .tran 0.5m 17m 。終わり ナツメグコマンド： setplot tran1 プロットv

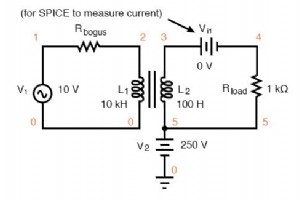
電気的絶縁のSPICE分析 変圧器は、AC回路とDC回路のさまざまなレベルの電圧と電流を簡単に変換できるほか、絶縁と呼ばれる非常に便利な機能も備えています。 、これは、直接配線接続を使用せずに、ある回路を別の回路に結合する機能です。 この効果の適用を別のSPICEシミュレーションで示すことができます。今回は、2つの回路の「アース」接続を示し、追加の電圧源を使用して1つの回路とアースの間に高いDC電圧を印加します。 トランスフォーマーは、V1の10VacをV2の250VDCから分離します。 v1 1 0 ac 10 sin rbogus1 1 2 1e-12 v2 5 0

これまで、一次巻線と二次巻線のインダクタンスが同じで、両方の回路でほぼ等しい電圧と電流レベルが得られる変圧器のシミュレーションを観察してきました。ただし、変圧器の一次側と二次側の間の電圧と電流の均等性は、すべての変圧器の標準ではありません。 2つの巻線のインダクタンスが等しくない場合、何か面白いことが起こります： トランスフォーマー v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 10000 l2 3 5100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac lin 1 60 6

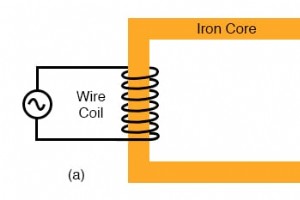
導電性コアに巻き付けられたインダクタの動作 強磁性体のループの周りに絶縁ワイヤのコイルを巻き付け、このコイルにAC電圧源で通電するとします:(下の図（a）） 強磁性ループの絶縁巻線には誘導性リアクタンスがあり、AC電流を制限します インダクターとして、この鉄心コイルは、誘導性リアクタンスで印加電圧に対抗し、次の式で予測されるようにコイルを流れる電流を制限すると予想されます。 X L =2πfLおよびI =E / X（またはI =E / Z） ただし、この例では、デバイス内の電圧、電流、磁束の相互作用をより詳細に調べる必要があります。 キルヒホッフの電

この章はこれまでのところ長いですが、フィルター設計の表面を傷つけ始めるだけです。 私の主張を証明するには、高度なフィルター設計の教科書をざっと読むだけで十分です。 コンポーネントの選択と周波数応答の予測に関係する数学は、控えめに言っても気が遠くなるようなものです。これは、最初の電子工学の学生の範囲をはるかに超えています。ここでの私の意図は、フィルターの性能を調査するためにSPICE回路解析プログラムの能力に頼って、可能な限り少ない計算でフィルター設計の基本原理を提示することでした。 このようなコンピュータシミュレーションソフトウェアの利点は、初心者の学生にとっても、働くエンジニアにとって

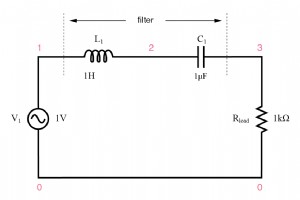
これまで、私たちが集中してきたフィルター設計は、どちらかを採用してきました。 コンデンサまたは インダクタですが、同時に両方を使用することはできません。 LとCの組み合わせは共振する傾向があり、この特性はバンドパスおよびバンドストップフィルター回路の設計に利用できることを今では知っておく必要があります。 直列LC回路は共振時に最小のインピーダンスを与え、並列LC（「タンク」）回路はそれらの共振周波数で最大のインピーダンスを与えます。これを知っているので、バンドパスフィルターまたはバンドストップフィルターのいずれかを設計するための2つの基本的な戦略があります。 バンドパスフィルターの場合、2

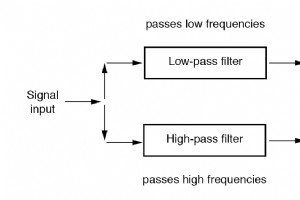
バンドストップフィルターを作成するには？ バンド除去とも呼ばれます 、バンドリジェクト 、またはノッチ フィルタ、この種のフィルタは、コンポーネント値によって設定された特定の範囲の上下のすべての周波数を通過させます。当然のことながら、バンドパス設計と同じように、ローパスフィルターとハイパスフィルターで作成できますが、今回は2つのフィルターセクションを直列ではなく並列に接続します。 バンドストップフィルターのシステムレベルのブロック図。 Twin-Tバンドストップフィルター 2つの容量性フィルターセクションを使用して構築され、次のようになります。 「Twi

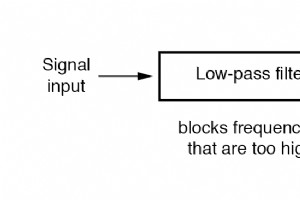
バンドパスフィルターの作成方法 特定の帯域、拡散、または周波数をより広い範囲の混合信号からフィルタリングする必要があるアプリケーションがあります。フィルタ回路は、ローパスとハイパスの特性を1つのフィルタに組み合わせることにより、このタスクを実行するように設計できます。結果はバンドパスと呼ばれます フィルタ。 ローパスフィルターとハイパスフィルターからバンドパスフィルターを作成する方法は、ブロック図を使用して説明できます。 バンドパスフィルターのシステムレベルのブロック図。 コンデンサを使用したバンドパスフィルターの設計 これらの2つのフィルター回路の直列の組み合わせから

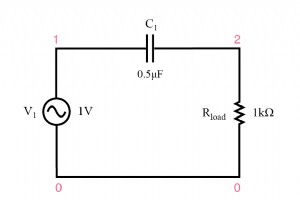
ハイパスフィルターのタスクは、ローパスフィルターの正反対です。つまり、高周波信号の通過を容易にし、低周波信号への通過を困難にします。ご想像のとおり、ハイパスフィルターの誘導性（下の図）バージョンと容量性（下の図）バージョンは、それぞれのローパスフィルターの設計とは正反対です。 容量性ハイパスフィルター。 コンデンサのインピーダンス コンデンサのインピーダンス（上の図）は、周波数が低くなるにつれて増加します。 （下の図）この直列の高インピーダンスは、低周波信号が負荷に達するのを妨げる傾向があります。 容量性ハイパスフィルター v1 1 0 ac 1 sin c1 1 2

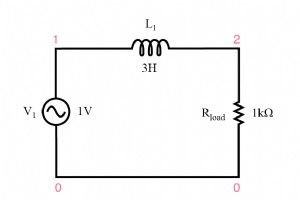
定義上、ローパスフィルタは、低周波信号への通過が容易で、高周波信号への通過が困難な回路です。この目的を達成できる回路には2つの基本的な種類があり、それぞれに多くのバリエーションがあります。誘導性ローパスフィルター（下図）と容量性ローパスフィルター（下図）です。 誘導ローパスフィルター 誘導ローパスフィルター インダクタのインピーダンスは、周波数の増加とともに増加します。この直列の高インピーダンスは、高周波信号が負荷に到達するのをブロックする傾向があります。これは、SPICE分析で実証できます:(下の図） 誘導ローパスフィルター v1 1 0 ac 1 sin l1 1

回路内の異なる周波数の混合物から1つの周波数または周波数範囲を選択的にフィルタリングできる回路が望ましい場合があります。この周波数選択を実行するように設計された回路は、フィルター回路と呼ばれます。 、または単にフィルタ 。 フィルタ回路の一般的なニーズは、最高の音質と電力効率を得るために特定の範囲の可聴周波数を増幅または抑制する必要がある高性能ステレオシステムです。 イコライザーに精通している可能性があります 、これにより、リスニングエリアのリスナーの好みと音響特性に合わせていくつかの周波数範囲の振幅を調整できます。 クロスオーバーネットワークにも精通している可能性があります 、特定の周

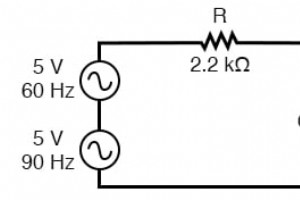
異なる周波数の一連の正弦波に相当する非正弦波の繰り返し波形の原理は、一般的な波の基本的な特性であり、AC回路の研究に非常に実用的です。 これは、完全に正弦波の形をしていない波形がある場合はいつでも、問題の回路が、異なる周波数の電圧の配列が一度に印加されているかのように反応することを意味します。 AC回路が周波数の混合からなる電源電圧にさらされると、その回路のコンポーネントは各構成周波数に異なる方法で応答します。コンデンサやインダクタなどのリアクティブコンポーネントは、回路に存在するすべての周波数に対して同時に固有のインピーダンスを示します。 ありがたいことに、このような回路の分析は、重ね

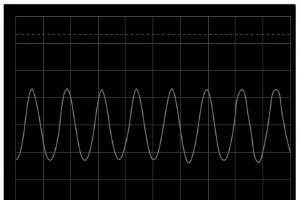
特に FFT の形式でのコンピューター化されたフーリエ解析 アルゴリズムは、波形とそれに関連するスペクトル成分の理解を深めるための強力なツールです。 .fourierオプションとしてSPICEシミュレータにプログラムされたこの同じ数学的ルーチンは、測定された信号に対してリアルタイムのフーリエ解析を実行するために、さまざまな電子テスト機器にもプログラムされています。 このセクションでは、このようなツールの使用といくつかの異なる波形の分析について説明します。 まず、523.25Hzの周波数の単純な正弦波があります。この特定の周波数値は、ピアノキーボードの「C」ピッチであり、「中央のC」の1オ

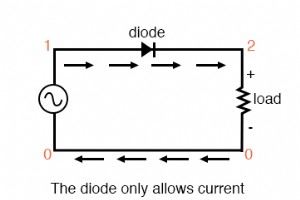
奇妙に思えるかもしれませんが、任意 繰り返しの非正弦波形は、実際には、異なる振幅と周波数の一連の正弦波形を足し合わせたものと同等です。方形波は非常に一般的でよく理解されているケースですが、それだけではありません。 トランジスタやシリコン制御整流子（ SCR ）などの電子電力制御デバイス ）多くの場合、電源からの「クリーンな」（純粋な）正弦波ACの本質的に切り刻まれたバージョンである電圧および電流波形を生成します。 これらのデバイスには、突然変更する機能があります 制御信号の電圧または電流の印加による抵抗。したがって、ほぼ瞬時に「オン」または「オフ」になり、回路に電力を供給するソース電圧波形

任意 繰り返される非正弦波は、さまざまな振幅と周波数でのDC電圧、正弦波、および/または正弦波（90度の位相シフトを持つ正弦波）の組み合わせと見なすことができます。 これは、問題の波形がどれほど奇妙で複雑であっても当てはまります。時間の経過とともに定期的に繰り返される限り、この一連の正弦波に還元できます。 特に、方形波は、同じ周波数の正弦波と、振幅が減少する無限の一連の奇数多重周波数の正弦波の合計と数学的に同等であることがわかっています。 波形についてのこの真実は、最初は信じられないほど奇妙に思えるかもしれません。ただし、方形波が実際に加算された無限の一連の正弦波高調波であ

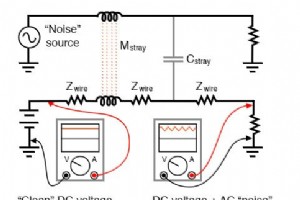
これまでのAC回路の研究では、単一周波数の正弦波電圧波形によって電力が供給される回路を調査しました。ただし、電子機器の多くのアプリケーションでは、単一周波数信号は規則ではなく例外です。 電圧の複数の周波数が同時に共存する回路に遭遇することがよくあります。また、回路波形は正弦波以外のものである可能性があります。その場合、それらを非正弦波と呼びます。 波形 。 さらに、DCがACと混合される状況、つまり波形が定常（DC）信号に重畳される状況に遭遇する可能性があります。 このような混合の結果、信号の強度は変化しますが、極性が変化したり、極性が非対称に変化したりすることはありません（たとえば

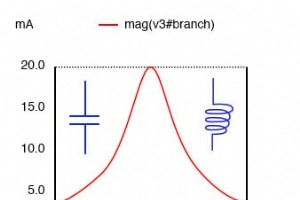
共振回路のQ（品質）係数は、共振回路の「良さ」または品質の尺度です。この性能指数の値が高いほど、帯域幅が狭くなり、多くのアプリケーションで望ましいことになります。より正式には、Qは、回路のリアクタンスと抵抗でそれぞれ消費される電力に対する蓄積された電力の比率です。 Q =P 保存済み / P 散逸 =I 2 X / I 2 R Q =X / Rここで、X =共振時の容量性または誘導性リアクタンスR =直列抵抗。 この式は、直列共振回路に適用できます。また、抵抗がインダクタと直列の場合は並列共振回路にも適用できます。これは、Qを制限するインダクタの抵抗に主に関係しているため

抵抗がほとんどまたはまったくない単純な無効回路では、インピーダンスが大幅に変化した場合の影響は、前述の式で予測された共振周波数で現れます。並列（タンク）LC回路では、これは共振時のインピーダンスが無限であることを意味します。直列LC回路では、共振時のインピーダンスがゼロであることを意味します。 ただし、ほとんどのLC回路にかなりのレベルの抵抗が導入されるとすぐに、この単純な共振の計算は無効になります。 このページでは、以前と同じ静電容量とインダクタンスの値を使用して、抵抗が追加されたいくつかのLC回路を見ていきます。それぞれ10 µFと100mHです。 高抵抗回路の共振周波数